Теория бесконечно малых деформаций

В механике сплошных сред теория бесконечно малых деформаций представляет собой математический подход к описание деформации твердого тела, в котором причинен ущерб материальных частиц, которые меньше других (действительно, бесконечно меньше), чем любой соответствующий размер тела; так что его геометрия и основные свойства материала (такие как плотность и жесткость ) в каждой точке пространства могут считаться в результате деформации.

При таком предположении уравнения механики сплошной среды значительно упрощаются. Этот подход также можно назвать теорией малых деформаций, теорией малых смещений или теорией малых смещений-градиентов . Это контрастирует с теорией конечных деформаций, где сделано противоположное предположение.

Теория применяемых в гражданском строительстве и машиностроении методов применения в гражданском строительстве и машиностроении для анализа напряжений конструкций, построенных из относительно жестких упругих материалов, таких как бетон и сталь, поскольку общей целью при проектировании таких конструкций является минимизация их деформации при типичных нагрузках. Это приближение требует осторожности в случае тонких гибких тел, таких как стержни, пластины и оболочки, которые подвержены значительному вращению, что делает результаты ненадежными.

• 1 Тензор бесконечно малых деформаций
  • 1.1 Геометрическое происхождение
  • 1.2 Физическая интерпретация
  • 1.3 Правила трансформации деформации
  • 1,4 Инварианты деформации
  • 1,5 Основные деформации
  • 1,6 Объемная деформация
  • 1,7 Тензор девиатора деформации
  • 1,8 Октаэдрическая деформация
  • 1,9 Эквивалентная деформация
• 2 Уравнения совместимости
• 3 Особые случаи
  • 3.1 Плоская деформация
  • 3.2 Антиплоскостная деформация
• 4 Тензор бесконечно малых вращений
  • 4.1 Осевой вектор
  • 4.2 Связь между тензором деформации и вектора вращения
  • 4.3 Связь между тензором и вектором вращения
• 5 Тензор деформации в цилиндрических координатах
• 6 Тензор деформации в сферических координатах
• 7 См. также
• 8 Ссылки
• 9 Внешние ссылки

Для бесконечно малой деформации состояния континуального тела , в котором градиент с ущербом ( тензор 2-го порядка) мал по сравнению с единицей, т.е. $\Vert \; \nabla \; U\; \Vert \; \ll \; 1\; \{\backslash \; displaystyle\; \backslash \; |\; \backslash \; nabla\; \backslash \; mathbf\; \{u\}\; \backslash \; |\; \backslash \; ll\; 1\}$, можно выполнить геометрическую линеаризацию любого из (бесконечных множеств) тензоров деформации, используемых в конечных деформациях, например тензор деформации Лагранжа $E\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{E\}\}$и тензор деформации Эйлера $e\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\}$. При такой линеаризации не крутятся нелинейные члены второго порядка тензора конечных деформаций. Таким образом, мы имеем

$E\; =\; 1\; 2\; (\nabla \; X\; u\; +\; (\nabla \; X\; u)\; T\; +\; (\nabla \; X\; u)\; T\; \nabla \; X\; u)\; \approx \; 1\; 2\; (\nabla \; X\; u\; +\; (\nabla \; X\; u)\; T)\; \{\; \backslash \; Displaystyle\; \backslash \; mathbf\; \{E\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (\backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{X\}\}\; \backslash \; mathbf\; \{u\}\; +\; (\backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{X\}\}\; \backslash \; mathbf\; \{u\})\; ^\; \{T\}\; +\; (\backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{X\}\}\; \backslash \; mathbf\; \{u\})\; ^\; \{T\}\; \backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{X\}\}\; \backslash \; mathbf\; \{u\}\; \backslash \; right)\; \backslash \; приблизительно\; \{\backslash \; гидроразрыв\; \{1\}\; \{2\}\}\; \backslash \; left\; (\backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{X\}\}\; \backslash \; mathbf\; \{u\}\; +\; (\backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{X\}\}\; \backslash \; mathbf\; \{u\})\; ^\; \{T\}\; \backslash \; right)\}$

или

$EKL\; =\; 1\; 2\; (\partial \; UK\; \partial \; XL\; +\; \partial \; UL\; \partial \; XK\; +\; \partial \; UM\; \partial \; XK\; \partial \; UM\; \partial \; XL)\; \approx \; 1\; 2\; (\partial \; UK\; \partial \; XL\; +\; \partial \; UL\; \partial \; XK)\; \{\; \backslash \; Displaystyle\; E\_\; \{KL\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; U\_\; \{K\}\}\; \{\backslash \; partial\; X\_\; \{L\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; U\_\; \{L)\; \}\})\; \{\backslash \; partial\; X\_\; \{K\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; U\_\; \{M\}\}\; \{\backslash \; partial\; X\_\; \{K\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; U\_\; \{M\}\}\; \{\backslash \; partial\; X\_\; \{L\; \}\}\}\; \backslash \; right)\; \backslash \; приблизительно\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; U\_\; \{K\}\}\; \{\backslash \; partial\; X\_\; \{L\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; U\_\; \{\; L\}\})\; \{\backslash \; partial\; X\_\; \{K\}\}\}\; \backslash \; right)\}$

и

$e\; Знак\; равно\; 1\; 2\; (\nabla \; xu\; +\; (\nabla \; xu)\; T\; -\; \nabla \; xu\; (\nabla \; xu)\; T)\; \approx \; 1\; 2\; (\nabla \; xu\; +\; (\nabla \; xu)\; T)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; =\; \{\backslash \; frac\; \{1\}\; \{\; 2\}\}\; \backslash \; left\; (\backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{x\}\}\; \backslash \; mathbf\; \{u\}\; +\; (\backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{x\}\}\; \backslash \; mathbf\; \{u\})\; ^\; \{T\}\; -\; \backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{x\}\}\; \backslash \; mathbf\; \{u\}\; (\backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{x\}\}\; \backslash \; mathbf\; \{u\})\; ^\; \{T\}\; \backslash \; right)\; \backslash \; приблизительно\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (\backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{x\}\}\; \backslash \; mathbf\; \{u\}\; +\; (\backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{x\}\}\; \backslash \; mathbf\; \{u\})\; ^\; \{T\}\; \backslash \; right)\}$

или

$ers\; =\; 1\; 2\; (\partial \; ур\; \partial \; xs\; +\; \partial \; нас\; \partial \; xr\; -\; \partial \; uk\; \partial \; xr\; \partial \; uk\; \partial \; xs)\; \approx \; 1\; 2\; (\partial \; ur\; \partial \; xs\; +\; \partial \; us\; \partial \; xr)\; \{\backslash \; displaystyle\; e\_\; \{rs\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{r\}\}\; \{\backslash \; partial\; x\_\; \{s\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{s\}\}\; \{\backslash \; partial\; x\_\; \{r\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; частичный\; u\_\; \{k\}\}\; \{\backslash \; partial\; x\_\; \{r\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{k\}\}\; \{\backslash \; partial\; x\_\; \{s\}\}\}\; \backslash \; right)\; \backslash \; приблизительно\; \{\backslash \; frac\; \{1\}\; \{2\; \}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{r\}\}\; \{\backslash \; partial\; x\_\; \{s\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{s\}\}\; \{\backslash \; partial\; x\_\; \{r\}\}\}\; \backslash \; right)\}$

Эта линеаризация подразумевает, что лагранжевое описание и эйлерово описание представляет собой, поскольку существует небольшая разница в материальных и пространственных координатах данной материальной точки в континууме. Следовательно, компоненты градиента с поверхности материала и градиента пространственного смещения равны. Таким образом, мы имеем

$E\; \approx \; e\; \approx \; \epsilon \; =\; 1\; 2\; ((\nabla \; u)\; T\; +\; \nabla \; u)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{E\}\; \backslash \; приблизительно\; \backslash \; mathbf\; \{e\}\; \backslash \; приблизительно\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\; \}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; ((\backslash \; nabla\; \backslash \; mathbf\; \{u\})\; ^\; \{T\}\; +\; \backslash \; nabla\; \backslash \; mathbf\; \{u\}\; \backslash \; right)\; \backslash \; qquad\}$

или $EKL\; \approx \; ers\; \approx \; \epsilon \; ij\; =\; 1\; 2\; (ui,\; j\; +\; uj,\; i)\; \{\backslash \; displaystyle\; \backslash \; qquad\; E\_\; \{KL\}\; \backslash \; приблизительно\; e\_\; \{rs\}\; \backslash \; приблизительно\; \backslash \; varepsilon\; \_\; \{ij\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\; \}\; \backslash \; left\; (u\_\; \{i,\; j\}\; +\; u\_\; \{j,\; i\}\; \backslash \; right)\}$

где $\epsilon \; ij\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{ij\}\}$- компоненты бесконечно малого тензор деформации $\epsilon \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\}$, также называемый тензором деформации Коши, тензором линейной деформации или тензором малых деформаций.

$ε ij = 1 2 (ui, j + uj, i) = [ε 11 ε 12 ε 13 ε 21 ε 22 ε 23 ε 31 ε 32 ε 33] = [∂ u 1 ∂ x 1 1 2 (∂ u 1 ∂ x 2 + ∂ u 2 ∂ x 1) 1 2 (∂ u 1 ∂ x 3 + ∂ u 3 ∂ x 1) 1 2 (∂ u 2 ∂ x 1 + ∂ u 1 ∂ x 2) ∂ u 2 ∂ x 2 1 2 (∂ u 2 ∂ x 3 + ∂ u 3 ∂ x 2) 1 2 (∂ u 3 ∂ x 1 + ∂ u 1 ∂ x 3) 1 2 (∂ u 3 ∂ x 2 + ∂ u 2) ∂ Икс 3) ∂ U 3 ∂ Икс 3] {\ Displaystyle {\ begin {Выровнено} \ varepsilon _ {ij} = {\ frac {1} {2}} \ left (u_ {i, j} + u_ {j, i} \ right) \\ = \ left [{\ begin {matrix} \ varepsilon _ {11} \ varepsilon _ {12} \ varepsilon _ {13} \\\ varepsilon _ {21} \ varepsilon _ {22} \ varepsilon _ {23} \\\ varepsilon _ {31} \ varepsilon _ {32} \ varepsilon _ {33} \\\ end {matrix}} \ right] \\ = \ left [{\ begin {matrix} {\ frac {\ partial u_ {1}} {\ partial x_ {1}}} {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {1}} {\ partial x_ {2}}} + {\ frac {\ partial u_ {2}} {\ partial x_ {1}}} \ right) {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {1}} {\ partial x_ {3}}} + {\ frac {\ partial u_ {3}} {\ partial x_ {1}}} \ right) \\ {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {2}} {\ partial x_ {1} }} + {\ frac {\ partial u_ {1}} {\ partial x_ {2}}} \ right) {\ frac {\ partial u_ {2}} {\ partial x_ {2}}} {\ frac {1} {2}} \ левый ({\ frac {\ partial u_ {2}} {\ partial x_ {3}}} + {\ frac {\ partial u_ {3}} {\ partial x_ {2}) }} \ right) \\ {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {3}} {\ partial x_ {1}}} + {\ frac {\ partial u_ {1 }} {\ partial x_ {3})}} \ right) {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {3}} {\ partial x_ {2}}} + {\ frac {\ partial u_ {2})} {\ partial x_ {3}}} \ right) {\ frac {\ partial u_ {3}} {\ partial x_ {3}}} \\\ end { матрица}} \ right] \ end {выровнено}}$

или используя другие обозначения:

$[ε xx ε xy ε xz ε yx ε yy ε yz ε zx ε zy ε zz] = [∂ ux ∂ x 1 2 (∂ ux ∂ y + ∂ uy ∂ x) 1 2 (∂ ux ∂ z + ∂ uz ∂ x) 1 2 (∂ uy ∂ x + ∂ ux ∂ y) ∂ uy ∂ y 1 2 (∂ uy ∂ z + ∂ uz ∂ y) 1 2 (∂ uz ∂ x + ∂ ux ∂ z) 1 2 (∂ uz ∂ y + ∂ uy ∂ z) ∂ uz ∂ z] {\ displaystyle \ left [{\ begin {matrix} \ varepsilon _ {xx} \ varepsilon _ {xy} \ varepsilon _ {xz} \\\ varepsilon _ {yx} \ varepsilon _ {yy} \ varepsilon _ { yz} \\\ varepsilon _ {zx} \ varepsilon _ {zy} \ varepsilon _ {zz} \\\ конец {ма trix}} \ right] = \ left [{\ begin {matrix} {\ frac { \ partial u_ {x}} {\ partial x}} {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {x}} {\ partial y}} + {\ frac {\ частичный u_ {y}} {\ partial x}} \ right) {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {x}} {\ partial z}} + {\ frac {\ partial u_ {z}} {\ partial x}} \ right) \\ {\ frac {1} {2}} \ слева ({\ frac {\ partial u_ {y}} {\ partial x}} + {\ frac {\ partial u_ {x}} {\ partial y}} \ right) {\ frac {\ partial u_ {y}} {\ partial y}} {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {y}} {\ partial z}} + {\ frac {\ partial u_ {z})} {\ partial y}} \ right) \\ {\ frac {1} { 2}} \ left ({\ frac {\ partial u_ {z}} {\ partial x}} + {\ frac {\ partial u_ {x}} {\ partial z}} \ right) {\ frac {1} {2}} \ left ({\ frac {\ partial u_ {z}} {\ partial y}} + {\ frac {\ partial u_ {y}} {\ partial z}} \ right) {\ frac {\ partial u_ {z}} {\ partial z}} \\\ end {matrix}} \ right]}$

Кроме того, поскольку градиент деформации может быть выражен как $F\; =\; \nabla \; u\; +\; I\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{F\}\}\; =\; \{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; mathbf\; \{u\}\; +\; \{\backslash \; полужирный\; символ\; \{I\}\}\}$где $I\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{I\}\}\}$- тождественный тензор второго порядка, у нас есть

$\epsilon \; =\; 1\; 2\; (FT\; +\; F)\; -\; I\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (\{\backslash \; boldsymbol\; \{F\}\}\; ^\; \{T\}\; +\; \{\backslash \; boldsymbol\; \{F\}\}\; \backslash \; right)\; -\; \{\backslash \; boldsymbol\; \{I\}\}\}$

Также из в общем выражении для лагранжевых и эйлеровых тензоров конечных деформаций, мы имеем

$E\; (m)\; =\; 1\; 2\; м\; (U\; 2\; m\; -\; I)\; =\; 1\; 2\; м\; [(FTF)\; m\; -\; I]\; \approx \; 1\; 2\; м\; [\{\nabla \; u\; +\; (\nabla \; u)\; T\; +\; I\}\; m\; -\; I]\; \approx \; \epsilon \; e\; (m)\; =\; 1\; 2\; м\; (V\; 2\; m\; -\; I)\; =\; 1\; 2\; м\; [(БПФ)\; m\; -\; I]\; \approx \; \epsilon \; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; mathbf\; \{E\}\; \_\; \{(m)\}\; =\; \{\backslash \; frac\; \{1\}\; \{2m\}\}\; (\backslash \; mathbf\; \{U\}\; ^\; \{2m\}\; -\; \{\backslash \; boldsymbol\; \{I\}\})\; =\; \{\backslash \; frac\; \{1\}\; \{2m\}\}\; [(\{\backslash \; boldsymbol\; \{F\}\}\; ^\; \{T\}\; \{\backslash \; boldsymbol\; \{F\}\})\; ^\; \{m\}\; -\; \{\backslash \; boldsymbol\; \{I\}\}]\; \backslash \; приблизительно\; \{\backslash \; frac\; \{1\}\; \{2m\}\}\; [\backslash \; \{\{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; mathbf\; \{\; u\}\; +\; (\{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; mathbf\; \{u\})\; ^\; \{T\}\; +\; \{\backslash \; boldsymbol\; \{I\}\}\; \backslash \}\; ^\; \{m\}\; -\; \{\backslash \; boldsymbol\; \{I\}\}]\; \backslash \; приблизительно\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; \backslash \backslash \backslash \; mathbf\; \{e\}\; \_\; \{(m)\}\; =\; \{\backslash \; frac\; \{1\}\; \{2m\}\}\; (\backslash \; mathbf\; \{V\}\; ^\; \{2m\}\; -\; \{\backslash \; boldsymbol\; \{I\}\})\; =\; \{\backslash \; frac\; \{1\}\; \{2m\}\}\; [(\{\backslash \; boldsymbol\; \{F\}\}\; \{\backslash \; boldsymbol\; \{F\}\}\; ^\; \{T\})\; ^\; \{m\}\; -\; \{\backslash \; boldsymbol\; \{I\}\}]\; \backslash \; приблизительно\; \{\backslash \; boldsymbol\; \{\; \backslash \; varepsilon\}\}\; \backslash \; end\; \{align\}\}\}$

Геометрический вывод

Рисунок 1. Два -мерная геометрическая деформация бесконечно малого материального элемента.

Рассмотрим двумерную деформацию бесконечно малого материального элемента с размерами $dx\; \{\backslash \; displaystyle\; dx\}$by $dy\; \{\backslash \; displaystyle\; dy\}$(рис. 1), который после деформации принимает форму ромба. Из геометрии рисунка 1 имеем

$ab\; ¯\; =\; (dx\; +\; \partial \; ux\; \partial \; xdx)\; 2\; +\; (\partial \; uy\; \partial \; xdx)\; 2\; =\; dx\; 1\; +\; 2\; \partial \; ux\; \partial \; x\; +\; (\partial \; ux\; \partial \; x)\; 2\; +\; (\partial \; uy\; \partial \; х)\; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; overline\; \{ab\}\}\; =\; \{\backslash \; sqrt\; \{\backslash \; left\; (dx\; +\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; x\}\}\; dx\; \backslash \; right)\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{y\}\}\; \{\backslash \; partial\; x\}\}\; dx\; \backslash \; right)\; ^\; \{2\}\}\}\; \backslash \backslash \; =\; dx\; \{\backslash \; sqrt\; \{1\; +\; 2\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; x\}\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; x\}\}\; \backslash \; right)\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{y\}\}\; \{\backslash \; partial\; x\}\}\; \backslash \; right)\; ^\; \{2\}\}\}\; \backslash \backslash \backslash \; end\; \{align\}\}\}$

Для очень малых градиентов с ущерба, т. е. $\Vert \; \nabla \; U\; \Vert \; \ll \; 1\; \{\backslash \; displaystyle\; \backslash \; |\; \backslash \; nabla\; \backslash \; mathbf\; \{u\}\; \backslash \; |\; \backslash \; ll\; 1\}$, мы имеем

$ab\; ¯\; \approx \; dx\; +\; \partial \; ux\; \partial \; xdx\; \{\backslash \; displaystyle\; \{\backslash \; overline\; \{ab\}\}\; \backslash \; приблизительно\; dx\; +\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; x\}\}\; dx\}$

нормальная деформация в $x\; \{\backslash \; displaystyle\; x\}$-направление прямоугольного элемента определяется как

$\epsilon \; x\; =\; ab\; ¯\; -\; AB\; ¯\; AB\; ¯\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{x\}\; =\; \{\backslash \; frac\; \{\{\backslash \; overline\; \{ab\}\}\; -\; \{\backslash \; overline\; \{AB\}\}\}\; \{\backslash \; overline\; \{AB\}\}\}\}$

и зная, что $AB\; ¯\; =\; dx\; \{\backslash \; displaystyle\; \{\backslash \; overline\; \{AB\}\}\; =\; dx\}$, мы имеем

$\epsilon \; x\; =\; \partial \; ux\; \partial \; x\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{x\}\; =\; \{\; \backslash \; frac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; x\}\}\}$

Аналогично, нормальная деформация в $y\; \{\backslash \; displaystyle\; y\}$-направление и $z\; \{\backslash \; displaystyle\; z\}$-направление, становится

$\epsilon \; y\; =\; \partial \; uy\; \partial \; y,\; \epsilon \; z\; =\; \partial \; uz\; \partial \; z\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{y\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{y\}\; \}\; \{\backslash \; partial\; y\}\}\; \backslash \; quad,\; \backslash \; qquad\; \backslash \; varepsilon\; \_\; \{z\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{z\}\}\; \{\backslash \; partial\; z\}\}\}$

инженерная деформация сд вига или изменение угла между двумя исходно ортогональными линиями материала, в данном случае линия $AC\; ¯\; \{\backslash \; displaystyle\; \{\backslash \; overline\; \{AC\}\}\}$и $AB\; ¯\; \{\backslash \; displaystyle\; \{\; \backslash \; overline\; \{AB\}\}\}$, определяется как

$\gamma \; xy\; =\; \alpha \; +\; \beta \; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{xy\}\; =\; \backslash \; alpha\; +\; \backslash \; beta\}$

Из геометрии рисунка 1 имеет

$tan\; \; \alpha \; =\; \partial \; uy\; \partial \; xdxdx\; +\; \partial \; ux\; \partial \; xdx\; =\; \partial \; uy\; \partial \; x\; 1\; +\; \partial \; ux\; \partial \; x,\; tan\; \; \beta \; =\; \partial \; ux\; \partial \; ydydy\; +\; \partial \; uy\; \partial \; ydy\; =\; \partial \; ux\; \partial \; Y\; 1\; +\; \partial \; uy\; \partial \; Y\; \{\backslash \; displaystyle\; \backslash \; tan\; \backslash \; alpha\; =\; \{\backslash \; frac\; \{\{\backslash \; dfrac\; \{\backslash \; partial\; u\_\; \{y\}\}\; \{\backslash \; partial\; x\}\}\; dx\}\; \{dx\; +\; \{\backslash \; dfrac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; x\; \}\}\; dx\}\}\; =\; \{\backslash \; frac\; \{\backslash \; dfrac\; \{\backslash \; partial\; u\_\; \{y\}\}\; \{\backslash \; partial\; x\}\}\; \{1\; +\; \{\backslash \; dfrac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; x\}\}\}\}\; \backslash \; quad,\; \backslash \; qquad\; \backslash \; tan\; \backslash \; beta\; =\; \{\backslash \; frac\; \{\{\backslash \; dfrac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; y\}\}\; dy\}\; \{dy\; +\; \{\backslash \; dfrac\; \{\backslash \; partial\; u\_\; \{y\}\}\; \{\backslash \; partial\; y\}\; \}\; dy\}\}\; =\; \{\backslash \; frac\; \{\backslash \; dfrac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; y\}\}\; \{1\; +\; \{\backslash \; dfrac\; \{\backslash \; partial\; u\_\; \{y\}\}\; \{\backslash \; partial\; y\}\}\}\}$

Для небольших поворотов, то есть $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$и $\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$$\ll \; 1\; \{\backslash \; displaystyle\; \backslash \; ll\; 1\}$мы имеем

$загар\; \; \alpha \; \approx \; \alpha ,\; загар\; \; \beta \; \approx \; \beta \; \{\backslash \; displaystyle\; \backslash \; tan\; \backslash \; alpha\; \backslash \; приблизительно\; \backslash \; альфа\; \backslash \; quad,\; \backslash \; qquad\; \backslash \; tan\; \backslash \; beta\; \backslash \; приблизительно\; \backslash \; beta\}$

и, опять же, для малых градиентов с ущерба, мы имеем

$\alpha \; =\; \partial \; uy\; \partial \; x,\; \beta \; =\; \partial \; ux\; \partial \; y\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; \{\backslash \; frac\; \{\backslash \; \backslash \; частичный\; u\_\; \{y\}\}\; \{\backslash \; partial\; x\}\}\; \backslash \; quad,\; \backslash \; qquad\; \backslash \; beta\; =\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; y\}\}\}$

, таким образом,

$\gamma \; xy\; =\; \alpha \; +\; \beta \; =\; \partial \; uy\; \partial \; x\; +\; \partial \; ux\; \partial \; y\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{xy\}\; =\; \backslash \; alpha\; +\; \backslash \; beta\; =\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{y\}\}\; \{\backslash \; partial\; x\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; y\}\}\}$

Поменяв местами $x\; \{\backslash \; displaystyle\; x\}$и $y\; \{\backslash \; displaystyle\; y\}$и $ux\; \{\backslash \; displaystyle\; u\_\; \{x\}\}$и $uy\; \{\backslash \; displaystyle\; u\_\; \{y\}\}$, можно показать, что $\gamma \; xy\; =\; \gamma \; yx\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{xy\}\; =\; \backslash \; gamma\; \_\; \{\; yx\}\}$

Аналогично, для $y\; \{\backslash \; displaystyle\; y\}$-$z\; \{\backslash \; displaystyle\; z\}$и $x\; \{\backslash \; displaystyle\; x\}$-$z\; \{\backslash \; displaystyle\; z\}$плоскости, у нас есть

$\gamma \; yz\; =\; \gamma \; zy\; =\; \partial \; uy\; \partial \; z\; +\; \partial \; uz\; \partial \; y,\; \gamma \; zx\; =\; \gamma \; xz\; =\; \partial \; uz\; \partial \; x\; +\; \partial \; ux\; \partial \; z\; \{\backslash \; Displaystyle\; \backslash \; gamma\; \_\; \{yz\}\; =\; \backslash \; gamma\; \_\; \{zy\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{y\}\}\; \{\backslash \; partial\; z\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{z\}\}\; \{\backslash \; partial\; y\}\}\; \backslash \; quad,\; \backslash \; qquad\; \backslash \; gamma\; \_\; \{zx\; \}\; =\; \backslash \; gamma\; \_\; \{xz\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{z\}\}\; \{\backslash \; partial\; x\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{x\}\}\; \{\backslash \; partial\; z\}\}\}$

Видно, компоненты тензорной деформации сдвига тензора бесконечно малых деформаций могут быть выражены с помощью определения деформации, $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$, как

$[\epsilon \; xx\; \epsilon \; xy\; \epsilon \; xz\; \epsilon \; yx\; \epsilon \; yy\; \epsilon \; yz\; \epsilon \; zx\; \epsilon \; zy\; \epsilon \; zz]\; =\; [\epsilon \; xx\; \gamma \; ху\; /\; 2\; \gamma \; xz\; /\; 2\; \gamma \; yx\; /\; 2\; \epsilon \; yy\; \gamma \; yz\; /\; 2\; \gamma \; zx\; /\; 2\; \gamma \; zy\; /\; 2\; \epsilon \; zz]\; \{\backslash \; displaystyle\; \backslash \; left\; [\{\backslash \; begin\; \{матрица\}\; \backslash \; varepsilon\; \_\; \{xx\}\; \backslash \; varepsilon\; \_\; \{xy\}\; \backslash \; varepsilon\; \_\; \{xz\}\; \backslash \backslash \backslash \; varepsilon\; \_\; \{yx\}\; \backslash \; varepsilon\; \_\; \{yy\}\; \backslash \; varepsilon\; \_\; \{yz\}\; \backslash \backslash \backslash \; varepsil\; на\; \_\; \{zx\}\; \backslash \; varepsilon\; \_\; \{zy\}\; \backslash \; varepsilon\; \_\; \{zz\}\; \backslash \backslash \backslash \; end\; \{matrix\}\}\; \backslash \; right]\; =\; \backslash \; left\; [\{\backslash \; begin\; \{matrix\}\; \backslash \; varepsilon\; \_\; \{xx\}\; \backslash \; gamma\; \_\; \{xy\}\; /\; 2\; \backslash \; gamma\; \_\; \{xz\}\; /\; 2\; \backslash \backslash \; \backslash \; gamma\; \_\; \{yx\}\; /\; 2\; \backslash \; varepsilon\; \_\; \{yy\}\; \backslash \; gamma\; \_\; \{yz\}\; /\; 2\; \backslash \backslash \backslash \; gamma\; \_\; \{zx\}\; /\; 2\; \backslash \; gamma\; \_\; \{zy\}\; /\; 2\; \backslash \; varepsilon\; \_\; \{zz\}\; \backslash \backslash \backslash \; end\; \{matrix\}\}\; \backslash \; right]\}$

Физическая интерпретация

Из теории конечных деформаций мы имеем

$dx\; 2\; -\; d\; X\; 2\; =\; d\; X\; \cdot \; 2\; E\; \cdot \; d\; X\; или\; (dx)\; 2\; -\; (d\; X)\; 2\; =\; 2\; EKL\; d\; XK\; d\; XL\; \{\backslash \; displaystyle\; d\; \backslash \; mathbf\; \{x\}\; ^\; \{2\}\; -d\; \backslash \; mathbf\; \{X\}\; ^\; \{2\}\; =\; d\; \backslash \; mathbf\; \{X\}\; \backslash \; cdot\; 2\; \backslash \; mathbf\; \{E\}\; \backslash \; cdot\; d\; \backslash \; mathbf\; \{X\}\; \backslash \; quad\; \{\backslash \; text\; \{или\}\}\; \backslash \; quad\; (dx)\; ^\; \{\; 2\}\; -\; (dX)\; ^\; \{2\}\; =\; 2E\_\; \{KL\}\; \backslash ,\; dX\_\; \{K\}\; \backslash ,\; dX\_\; \{L\}\}$

Для бесконечно малых деформаций мы

$dx\; 2\; -\; d\; X\; 2\; =\; d\; X\; \cdot \; 2\; \epsilon \; \cdot \; d\; Икс\; или\; (dx)\; 2\; -\; (d\; X)\; 2\; знак\; равно\; 2\; \epsilon \; KL\; d\; XK\; d\; XL\; \{\backslash \; displaystyle\; d\; \backslash \; mathbf\; \{x\}\; ^\; \{2\}\; -d\; \backslash \; mathbf\; \{X\}\; ^\; \{2\}\; =\; d\; \backslash \; mathbf\; \{X\}\; \backslash \; cdot\; 2\; \backslash \; mathbf\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; \backslash \; cdot\; d\; \backslash \; mathbf\; \{X\}\; \backslash \; quad\; \{\backslash \; text\; \{или\}\}\; \backslash \; quad\; (dx)\; ^\; \{2\; \}\; -\; (dX)\; ^\; \{2\}\; =\; 2\; \backslash \; varepsilon\; \_\; \{KL\}\; \backslash ,\; dX\_\; \{K\}\; \backslash ,\; dX\_\; \{L\}\}$

Деление на $(d\; X)\; 2\; \{\backslash \; displaystyle\; (dX)\; ^\; \{2\}\}$мы имеем

$dx\; -\; d\; X\; d\; X\; dx\; +\; d\; X\; d\; X\; =\; 2\; \epsilon \; ijd\; X\; id\; X\; d\; X\; jd\; X\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dx-dX\}\; \{\; dX\}\}\; \{\backslash \; frac\; \{dx\; +\; dX\}\; \{dX\}\}\; =\; 2\; \backslash \; varepsilon\; \_\; \{ij\}\; \{\backslash \; frac\; \{dX\_\; \{i\}\}\; \{dX\}\}\; \{\backslash \; frac\; \{dX\_\; \{j\}\}\; \{dX\}\}\}$

Для небольших деформаций мы предполагаем, что $dx\; \approx \; d\; X\; \{\backslash \; displaystyle\; dx\; \backslash \; приблизительно\; dX\}$, таким образом, второй член левой части становится: $dx\; +\; d\; X\; d\; X\; \approx \; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dx\; +\; dX\}\; \{dX\}\}\; \backslash \; приблизительно\; 2\}$.

Тогда мы имеем

$dx\; -\; d\; X\; d\; X\; =\; \epsilon \; ij\; N\; i\; N\; j\; =\; N\; \cdot \; \epsilon \; \cdot \; N\; \{\; \backslash \; displaystyle\; \{\backslash \; frac\; \{dx-dX\}\; \{dX\}\}\; =\; \backslash \; varepsilon\; \_\; \{ij\}\; N\_\; \{i\}\; N\_\; \{j\}\; =\; \backslash \; mathbf\; \{N\}\; \backslash \; cdot\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; \backslash \; cdot\; \backslash \; mathbf\; \{\; N\}\}$

где $N\; i\; =\; d\; X\; id\; X\; \{\backslash \; стиль\; отображения\; N\_\; \{i\}\; =\; \{\backslash \; frac\; \{dX\_\; \{i\}\}\; \{dX\}\}\}$, является единичным вектором в направлении $d\; X\; \{\backslash \; displaystyle\; d\; \backslash \; mathbf\; \{X\}\}$, а выражение в левой части - это нормальная деформация $e\; (N)\; \{\backslash \; displaystyle\; e\; \_\; \{(\backslash \; mathbf\; \{N\})\}\}$в направлении $N\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{N\}\}$. Для частного случая $N\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{N\}\}$в направлении $X\; 1\; \{\backslash \; displaystyle\; X\_\; \{1\}\}$, т. Е. $N\; =\; I\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{N\}\; =\; \backslash \; mathbf\; \{I\}\; \_\; \{1\}\}$, мы имеем

$e\; (I\; 1)\; =\; I\; 1\; \cdot \; \epsilon \; \cdot \; I\; 1\; знак\; равно\; \epsilon \; 11\; \{\backslash \; Displaystyle\; е\; \_\; \{(\backslash \; mathbf\; \{I\}\; \_\; \{1\})\}\; =\; \backslash \; mathbf\; \{I\}\; \_\; \{1\}\; \backslash \; cdot\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; \backslash \; cdot\; \backslash \; mathbf\; \{I\}\; \_\; \{1\}\; =\; \backslash \; varepsilon\; \_\; \{11\}\}$

Аналогично для $N\; =\; I\; 2\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{N\}\; =\; \backslash \; mathbf\; \{I\}\; \_\; \{2\}\}$и $N\; =\; I\; 3\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{N\}\; =\; \backslash \; mathbf\; \{I\}\; \_\; \{3\}\}$мы можем найти нормальные деформации $\epsilon \; 22\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{22\}\; \}$и $\epsilon \; 33\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{33\}\}$соответственно. Следовательно, диагональные элементы тензора бесконечно малых деформаций являются нормальными деформациями в координатных направлениях.

Правила преобразования деформации

Если мы выберем ортонормированную систему координат ($e\; 1,\; e\; 2,\; e\; 3\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{1\; \},\; \backslash \; mathbf\; \{e\}\; \_\; \{2\},\; \backslash \; mathbf\; \{e\}\; \_\; \{3\}\}$) мы можем записать тензор в терминах компонентов по отношению к этому базовым инструментам как

$\epsilon \; Знак\; равно\; \sum \; я\; знак\; равно\; 1\; 3\; \sum \; J\; знак\; равно\; 1\; 3\; \epsilon \; ijei\; \otimes \; ej\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{3\}\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{3\; \}\; \backslash \; varepsilon\; \_\; \{ij\}\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\; \backslash \; otimes\; \backslash \; mathbf\; \{e\}\; \_\; \{j\}\}$

В матричной форме

$\epsilon \; \_\; \_\; =\; [\epsilon \; 11\; \epsilon \; 12\; \epsilon \; 13\; \epsilon \; 12\; \epsilon \; 22\; \epsilon \; 23\; \epsilon \; 13\; \epsilon \; 23\; \epsilon \; 33]\; \{\backslash \; Displaystyle\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; varepsilon\; \_\; \{11\}\; \backslash \; varepsilon\; \_\; \{12\}\; \backslash \; varepsilon\; \_\; \{13\}\; \backslash \backslash \backslash \; varepsilon\; \_\; \{12\}\; \backslash \; varepsilon\; \_\; \{22\}\; \backslash \; varepsilon\; \_\; \{23\}\; \backslash \backslash \backslash \; varepsilon\; \_\; \{13\}\; \backslash \; varepsilon\; \_\; \{23\}\; \backslash \; varepsilon\; \_\; \{33\; \}\; \backslash \; end\; \{bmatrix\}\}\}$

Мы можем легко выбрать другую ортонормированную систему ко ординат ($e\; ^\; 1,\; e\; ^\; 2,\; e\; ^\; 3\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{e\}\})\}\; \_\; \{1\},\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{e\}\}\}\; \_\; \{2\; \},\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{e\}\}\}\; \_\; \{3\}\}$ ) вместо этого. В этом случае компоненты тензора разные, скажем

$\epsilon \; =\; \sum \; i\; =\; 1\; 3\; \sum \; j\; =\; 1\; 3\; \epsilon \; ^\; ije\; ^\; i\; \otimes \; e\; ^\; j\; ⟹\; \epsilon \; ^\; \_\; \_\; =\; [\epsilon \; ^\; 11\; \epsilon \; ^\; 12\; \epsilon \; ^\; 13\; \epsilon \; ^\; 12\; \epsilon \; ^\; 22\; \epsilon \; ^\; 23\; \epsilon \; ^\; 13\; \epsilon \; ^\; 23\; \epsilon \; ^\; 33]\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{3\}\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{3\}\; \{\backslash \; hat\; \{\backslash \; varepsilon\}\}\; \_\; \{ij\}\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{e\}\}\}\; \_\; \{i\}\; \backslash \; otimes\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{e\}\}\}\; \_\; \{j\}\; \backslash \; quad\; \backslash \; подразумевает\; \backslash \; quad\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; hat\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; hat\; \{\backslash \; varepsilon\}\}\; \_\; \{11\}\; \{\backslash \; hat\; \{\backslash \; varepsilon\}\}\; \_\; \{12\}\; \{\backslash \; hat\; \{\backslash \; varepsilon\}\}\; \_\; \{13\}\; \backslash \backslash \; \{\backslash \; hat\; \{\backslash \; varepsilon\}\}\; \_\; \{12\}\; \{\backslash \; hat\; \{\backslash \; varepsilon\}\}\; \_\; \{22\}\; \{\backslash \; hat\; \{\backslash \; varepsilon\}\}\; \_\; \{23\}\; \backslash \backslash \; \{\backslash \; hat\; \{\backslash \; varepsilon\}\}\; \_\; \{13\}\; \{\backslash \; hat\; \{\backslash \; varepsilon\}\}\; \_\; \{23\}\; \{\backslash \; hat\; \{\backslash \; varepsilon\}\}\; \_\; \{33\}\; \backslash \; end\; \{\; bmatrix\}\}$

Компоненты деформации в двух системах с использованием ресурсов

$\epsilon \; ^\; ij\; =\; \ell \; ip\; \ell \; jq\; \epsilon \; pq\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; varepsilon\}\}\; \_\; \{ij\}\; =\; \backslash \; ell\; \_\; \{ip\}\; ~\; \backslash \; ell\; \_\; \{jq\}\; ~\; \backslash \; varepsilon\; \_\; \{pq\}\}$

где использо валось соглашение о суммировании Эйнштейна для повторяющихся индексов и $\ell \; ij\; =\; е\; ^\; я\; \cdot \; ej\; \{\backslash \; displaystyle\; \backslash \; ell\; \_\; \{ij\}\; =\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{e\}\}\}\; \_\; \{i\; \}\; \backslash \; cdot\; \backslash \; mathbf\; \{e\}\; \_\; \{j\}\}$. В матричной форме

$\epsilon \; ^\; \_\; \_\; =\; L\; \_\; \_\; \epsilon \; \_\; \_\; L\; \_\; \_\; T\; \{\backslash \; displaystyle\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; hat\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\}\}\}\; =\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; mathbf\; \{L\}\}\}\}\; ~\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\}\}\; ~\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; mathbf\; \{L\}\}\}\}\; ^\; \{T\}\}$

или

$[ε ^ 11 ε ^ 12 ε ^ 13 ε ^ 21 ε ^ 22 ε ^ 23 ε ^ 31 ε ^ 32 ε ^ 33] = [ℓ 11 ℓ 12 ℓ 13 ℓ 21 ℓ 22 ℓ 23 ℓ 31 ℓ 32 ℓ 33] [ε 11 ε 12 ε 13 ε 21 ε 22 ε 23 ε 31 ε 32 ε 33] [ℓ 11 ℓ 12 ℓ 13 ℓ 21 ℓ 22 ℓ 23 ℓ 31 ℓ 32 ℓ 33] T {\ displaystyle { \ begin {bmatrix} {\ hat {\ varepsilon}} _ {11} {\ hat {\ varepsilon}} _ {12} {\ hat {\ varepsilon}} _ {13} \\ {\ hat {\ varepsilon}} _ {21} {\ hat {\ varepsilon}} _ {22} {\ hat {\ varepsilon}} _ {23} \\ {\ hat {\ varepsilon}} _ {31} {\ hat {\ varepsilon}} _ {32} {\ hat {\ varepsilon}} _ {33} \ end {bmatrix}} = {\ begin {bmatrix} \ ell _ {11} \ ell _ {12} \ ell _ {13} \\\ ell _ {21} \ ell _ {22} \ ell _ {23} \\\ ell _ {31} \ ell _ {32} \ ell _ {33} \ end {bmatrix}} {\ begin {bmatrix} \ varepsilon _ {11} \ varepsilon _ {12} \ varepsilon _ {13} \\\ varepsil на _ {21} \ varepsilon _ {22} \ varepsilon _ {23} \\\ varepsilon _ {31} \ varepsilon _ {32} \ varepsilon _ {33} \ end {bmatrix}} {\ begin {bmatrix} \ ell _ {11} \ ell _ {12} \ ell _ {13} \\\ ell _ {21} \ ell _ {22} \ ell _ {23} \\\ ell _ {31} \ ell _ {32 } \ ell _ {33} \ end {bmatrix}} ^ {T}}$

Инварианты деформации

Некоторые операции с тензором деформации дают тот же результат без относительно того, какая ортонормированная система координат используется для представления компонентов деформации. Результаты этих операций называются инвариантами деформации . Наиболее часто используемые инварианты деформации:

$I\; 1\; =\; tr\; (\epsilon )\; I\; 2\; =\; 1\; 2\; \{[tr\; (\epsilon )]\; 2\; -\; tr\; (\epsilon \; 2)\}\; I\; 3\; =\; det\; (\epsilon )\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{\; выровнено\}\; I\_\; \{1\}\; =\; \backslash \; mathrm\; \{tr\}\; (\{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\})\; \backslash \backslash \; I\_\; \{2\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \; \{[\backslash \; mathrm\; \{tr\}\; (\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\})]\; ^\; \{2\}\; -\; \backslash \; mathrm\; \{tr\}\; (\{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; ^\; \{2\})\; \backslash \}\; \backslash \backslash \; I\_\; \{3\}\; =\; \backslash \; det\; (\{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\})\; \backslash \; end\; \{align\}\}\}$

В терминах компонентов

$I\; 1\; =\; \epsilon \; 11\; +\; \epsilon \; 22\; +\; \epsilon \; 33\; I\; 2\; =\; \epsilon \; 12\; 2\; +\; \epsilon \; 23\; 2\; +\; \epsilon \; 31\; 2\; -\; \epsilon \; 11\; \epsilon \; 22\; -\; \epsilon \; 22\; \epsilon \; 33\; -\; \epsilon \; 33\; \epsilon \; 11\; I\; 3\; =\; \epsilon \; 11\; (\epsilon \; 22\; \epsilon \; 33\; -\; \epsilon \; 23\; 2)\; -\; \epsilon \; 12\; (\epsilon \; 11\; \epsilon \; 33\; -\; \epsilon \; 23\; \epsilon \; 31)\; +\; \epsilon \; 13\; (\epsilon \; 21\; \epsilon \; 32\; -\; \epsilon \; 22\; \epsilon \; 31)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; I\_\; \{1\}\; =\; \backslash \; varepsilon\; \_\; \{11\}\; +\; \backslash \; varepsilon\; \_\; \{22\}\; +\; \backslash \; varepsilon\; \_\; \{33\}\; \backslash \backslash \; I\_\; \{2\}\; =\; \backslash \; varepsilon\; \_\; \{12\}\; ^\; \{2\}\; +\; \backslash \; varepsilon\; \_\; \{23\}\; ^\; \{2\}\; +\; \backslash \; varepsilon\; \_\; \{31\}\; ^\; \{2\}\; -\; \backslash \; varepsilon\; \_\; \{11\}\; \backslash \; varepsilon\; \_\; \{22\}\; -\; \backslash \; varepsilon\; \_\; \{22\}\; \backslash \; varepsilon\; \_\; \{33\}\; -\; \backslash \; varepsilon\; \_\; \{33\}\; \backslash \; varepsilon\; \_\; \{11\}\; \backslash \backslash \; I\_\; \{3\}\; =\; \backslash \; varepsil\; на\; \_\; \{11\}\; (\backslash \; varepsilon\; \_\; \{22\}\; \backslash \; varepsilon\; \_\; \{33\}\; -\; \backslash \; varepsilon\; \_\; \{23\}\; ^\; \{2\})\; -\; \backslash \; varepsilon\; \_\; \{12\}\; (\backslash \; varepsilon\; \_\; \{11\}\; \backslash \; varepsilon\; \_\; \{33\}\; -\; \backslash \; varepsilon\; \_\; \{23\}\; \backslash \; varepsilon\; \_\; \{31\})\; +\; \backslash \; varepsilon\; \_\; \{13\}\; (\backslash \; varepsilon\; \_\; \{21\}\; \backslash \; varepsilon\; \_\; \{32\}\; -\; \backslash \; varepsilon\; \_\; \{22\}\; \backslash \; varepsilon\; \_\; \{31\})\; \backslash \; end\; \{align\}\}\}$

Основные деформации

Можно показать, что можно найти систему координат ($n\; 1,\; n\; 2,\; n\; 3\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{n\}\; \_\; \{1\},\; \backslash \; mathbf\; \{n\}\; \_\; \{2\},\; \backslash \; mathbf\; \{n\}\; \_\; \{3\}\}$), в компонентах тензора деформации

$\epsilon \; \_\; \_\; =\; [\epsilon \; 1\; 0\; 0\; 0\; \epsilon \; 2\; 0\; 0\; 0\; \epsilon \; 3]\; ⟹\; \epsilon \; знак\; равно\; \epsilon \; 1\; N\; 1\; \otimes \; N\; 1\; +\; \epsilon \; 2\; N\; 2\; \otimes \; N\; 2\; +\; \epsilon \; 3\; N\; 3\; \otimes \; N\; 3\; \{\backslash \; Displaystyle\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; varepsilon\; \_\; \{1\}\; 0\; 0\; \backslash \backslash \; 0\; \backslash \; varepsilon\; \_\; \{2\}\; 0\; \backslash \backslash \; 0\; 0\; \backslash \; varepsilon\; \_\; \{3\}\; \backslash \; конец\; \{bmatrix\}\}\; \backslash \; quad\; \backslash \; подразумевает\; \backslash \; quad\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; =\; \backslash \; varepsilon\; \_\; \{1\}\; \backslash \; mathbf\; \{n\}\; \_\; \{1\}\; \backslash \; otimes\; \backslash \; mathbf\; \{n\}\; \_\; \{1\}\; +\; \backslash \; varepsilon\; \_\; \{2\}\; \backslash \; mathbf\; \{n\; \}\; \_\; \{2\}\; \backslash \; ot\; imes\; \backslash \; mathbf\; \{n\}\; \_\; \{2\}\; +\; \backslash \; varepsilon\; \_\; \{3\}\; \backslash \; mathbf\; \{n\}\; \_\; \{3\}\; \backslash \; otimes\; \backslash \; mathbf\; \{n\}\; \_\; \{3\}\}$

Компоненты тензора деформации в ($n\; 1,\; n\; 2,\; n\; 3\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{n\}\; \_\; \{1\},\; \backslash \; mathbf\; \{n\}\; \_\; \{2\},\; \backslash \; mathbf\; \{n\}\; \_\; \{3\}\}$) системы координат называются главными деформациями и направлениями $ni\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{n\}\; \_\; \{i\}\}$называются направлениями основной деформации. В этой системе координат нет компонентов деформации, главные деформации представляют собой максимальное и минимальное растяжение элемента преобразования.

Если нам заданы компоненты тензора деформаций в произвольной ортонормированной системе координат, мы можем найти главные деформации, используя разложение по собственным значениям, определенное путем решения системы уравнений

$(\epsilon \; \_\; \_\; -\; \epsilon \; я\; я\; \_\; \_)\; ni\; знак\; равно\; 0\; \_\; \{\backslash \; displaystyle\; (\{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\}\}\}\}\; -\; \backslash \; varepsilon\; \_\; \{i\}\; ~\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; mathbf\; \{I\; \}\}\}\})\; ~\; \backslash \; mathbf\; \{n\}\; \_\; \{i\}\; =\; \{\backslash \; underline\; \{\backslash \; mathbf\; \{0\}\}\}\}$

Эта система эквивалентна сопоставлению вектора $ni\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{n\}\; \_\; \{i\}\}$, вдоль которого тензор деформации становится чистым растяжением без компонента сдвига.

Объемная деформация

Расширение (относительное изменение объема) - это след тензора:

$\delta \; =\; \Delta \; VV\; 0\; =\; \epsilon \; 11\; +\; \epsilon \; 22\; +\; \epsilon \; 33\; \{\backslash \; displaystyle\; \backslash \; delta\; =\; \{\backslash \; frac\; \{\backslash \; Delta\; V\}\; \{V\_\; \{0\}\}\}\; =\; \backslash \; varepsilon\; \_\; \{11\}\; +\; \backslash \; varepsilon\; \_\; \{22\}\; +\; \backslash \; varepsilon\; \_\; \{33\}\}$

Фактически, если мы рассматриваем куб с длиной ребра a, это квазикуб после деформации (изменение углов не меняет объем) с размерами $a\; \cdot \; (1\; +\; \epsilon \; 11)\; \times \; a\; \cdot \; (1\; +\; \epsilon \; 22)\; \times \; a\; \cdot \; (1\; +\; \epsilon \; 33)\; \{\backslash \; displaystyle\; a\; \backslash \; cdot\; (1+\; \backslash \; varepsilon\; \_\; \{11\})\; \backslash \; times\; a\; \backslash \; cdot\; (1+\; \backslash \; varepsilon\; \_\; \{22\})\; \backslash \; times\; a\; \backslash \; cdot\; (1+\; \backslash \; varepsilon\; \_\; \{33\})\}$и V 0 = a, поэтому

$\Delta \; VV\; 0\; =\; (1\; +\; \epsilon \; 11\; +\; \epsilon \; 22\; +\; \epsilon \; 33\; +\; \epsilon \; 11\; \cdot \; \epsilon \; 22\; +\; \epsilon \; 11\; \cdot \; \epsilon \; 33\; +\; \epsilon \; 22\; \cdot \; \epsilon \; 33\; +\; \epsilon \; 11\; \cdot \; \epsilon \; 22\; \cdot \; \epsilon \; 33)\; \cdot \; a\; 3\; -\; a\; 3\; a\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; Delta\; V\}\; \{V\_\; \{0\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; left\; (1+\; \backslash \; varepsilon\; \_\; \{11\; \}\; +\; \backslash \; varepsilon\; \_\; \{22\}\; +\; \backslash \; varepsilon\; \_\; \{33\}\; +\; \backslash \; varepsilon\; \_\; \{11\}\; \backslash \; cdot\; \backslash \; varepsilon\; \_\; \{22\}\; +\; \backslash \; varepsilon\; \_\; \{11\}\; \backslash \; cdot\; \backslash \; varepsilon\; \_\; \{33\}\; +\; \backslash \; varepsil\; на\; \_\; \{22\}\; \backslash \; cdot\; \backslash \; var\; эпсилон\; \_\; \{33\}\; +\; \backslash \; varepsilon\; \_\; \{11\}\; \backslash \; cdot\; \backslash \; varepsilon\; \_\; \{22\}\; \backslash \; cdot\; \backslash \; varepsilon\; \_\; \{33\}\; \backslash \; right)\; \backslash \; cdot\; a\; ^\; \{3\}\; -a\; ^\; \{3\}\}\; \{a\; ^\; \{3\}\}\}\}$

с учетом малых деформаций

$1\; \gg \; \epsilon \; ii\; \gg \; \epsilon \; ii\; \cdot \; \epsilon \; jj\; \gg \; \epsilon \; 11\; \cdot \; \epsilon \; 22\; \cdot \; \epsilon \; 33\; \{\backslash \; displaystyle\; 1\; \backslash \; gg\; \backslash \; varepsilon\; \_\; \{ii\}\; \backslash \; gg\; \backslash \; varepsilon\; \_\; \{ii\}\; \backslash \; cdot\; \backslash \; varepsilon\; \_\; \{jj\}\; \backslash \; gg\; \backslash \; varepsilon\; \_\; \{11\}\; \backslash \; cdot\; \backslash \; varepsilon\; \_\; \{22\}\; \backslash \; cdot\; \backslash \; varepsilon\; \_\; \{33\}\}$

следовательно, формула.

. Реальное изменение объема (вверху) и приблизительное (внизу): зеленый рисунок показывает расчетный объем, оранжевый рисунок - неучтенный объем

В случае чистого сдвига мы можем видеть, что нет изменения громкость.

Тензор девиатора деформации

Тензор бесконечно малых деформаций $\epsilon \; ij\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{ij\}\}$, аналогично тензору напряжений Коши, может быть выражен сумма как двух других тензоров:

1. a тензор средней деформации или тензор объемной деформации или тензор сферической деформации, $\epsilon \; M\; \delta \; ij\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{M\}\; \backslash \; delta\; \_\; \{ij\}\}$, относящийся к расширению или изменению объема; и
2. девиаторный компонент, называемый тензором девиатора деформации, $\epsilon \; ij\; \text{'}\{\backslash \; displaystyle\; \backslash \; varepsilon\text{'}\; \_\; \{ij\}\}$, относящийся к искажению.

$\epsilon \; ij\; =\; \epsilon \; ij\; \prime \; +\; \epsilon \; M\; \delta \; ij\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{ij\}\; =\; \backslash \; varepsilon\; \text{'}\_\; \{ij\}\; +\; \backslash \; varepsilon\; \_\; \{M\}\; \backslash \; delta\; \_\; \{ij\}\}$

где $\epsilon \; M\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{M\}\}$- средняя деформация, определяемая по формуле

$\epsilon \; M\; =\; \epsilon \; kk\; 3\; =\; \epsilon \; 11\; +\; \epsilon \; 22\; +\; \epsilon \; 33\; 3\; =\; 1\; 3\; I\; 1\; е\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{M\}\; =\; \{\backslash \; frac\; \{\backslash \; varepsilon\; \_\; \{kk\}\}\; \{3\}\}\; =\; \{\backslash \; frac\; \{\backslash \; varepsilon\; \_\; \{11\}\; +\; \backslash \; varepsilon\; \_\; \{22\}\; +\; \backslash \; varepsilon\; \_\; \{\; 33\}\}\; \{3\}\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{3\}\}\; I\_\; \{1\}\; ^\; \{e\}\}$

Девиаторный тензор деформации может быть получен путем вычитания тензора средней деформации из тензора бесконечно малых деформаций:

$ε ij ′ = ε ij - ε kk 3 δ ij [ε 11 ′ ε 12 ′ ε 13 ′ ε 21 ′ ε 22 ′ ε 23 ′ ε 31 ′ ε 32 ′ ε 33 ′] = [ε 11 ε 12 ε 13 ε 21 ε 22 ε 23 ε 31 ε 32 ε 33] - [ε M 0 0 0 ε M 0 0 0 ε M] = [ε 11 - ε M ε 12 ε 13 ε 21 ε 22 - ε M ε 23 ε 31 ε 32 ε 33 - ε M] {\ Displaystyle {\ begin {align} \ \ varepsi lon '_ {ij} = \ varepsilon _ {ij} - {\ frac {\ varepsilon _ {kk}} {3}} \ дельта _ {ij} \\\ влево [{\ begin {matrix} \ varepsilon '_ {11} \ varepsilon' _ {12} \ varepsilon '_ {13} \\\ varepsilon' _ {21} \ varepsilon '_ {22} \ varepsilon '_ {23} \\\ varepsilon' _ {31} \ varepsilon '_ {32} \ varepsilon' _ {33} \\\ end {matrix}} \ right] = \ left [{\ begin { матрица} \ varepsilon _ {11} \ varepsilon _ {12} \ varepsilon _ {13} \\\ varepsilon _ {21} \ varepsilon _ {22} \ varepsilon _ {23} \\\ varepsilon _ { 31} \ varepsilon _ {32} \ varepsilon _ {33} \\\ end {matrix}} \ right] - \ left [{\ begin {matrix} \ varepsilon _ {M} 0 0 \\ 0 \ varepsilon _ {M} 0 \\ 0 0 \ varepsilon _ {M} \\\ end {matrix}} \ right] \\ = \ left [{\ begin {matrix} \ varepsilon _ {11 } - \ varepsilon _ {M} \ varepsilon _ {12} \ varepsilon _ {13} \\\ varepsilon _ {21} \ varepsilon _ {22} - \ varepsilon _ {M} \ varepsilon _ {23 } \\\ varepsilon _ {31} \ varepsilon _ {32} \ varepsilon _ {33} - \ varepsilon _ {M} \\\ end {matrix}} \ right] \\\ end {align}}}$

Октаэдрический ие деформации

Пусть ($n\; 1\; N\; 2,\; N\; 3\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{n\}\; \_\; \{1\},\; \backslash \; mathbf\; \{n\}\; \_\; \{2\},\; \backslash \; mathbf\; \{n\}\; \_\; \{\; 3\}\}$) - направления трех основных деформаций. Октаэдрическая плоскость - это плоскость, нормаль которой образует равные углы с тремя главными направлениями. Техническая деформация сдвига на октаэдрической плоскости называется октаэдрической деформацией сдвига и определяется как

$\gamma \; oct\; =\; 2\; 3\; (\epsilon \; 1\; -\; \epsilon \; 2)\; 2\; +\; (\epsilon \; 2\; -\; \epsilon \; 3)\; 2\; +\; (\epsilon \; 3\; -\; \epsilon \; 1)\; 2\; \{\backslash \; Displaystyle\; \backslash \; gamma\; \_\; \{\backslash \; mathrm\; \{oct\}\}\; =\; \{\backslash \; tfrac\; \{2\}\; \{3\}\}\; \{\backslash \; sqrt\; \{(\backslash \; varepsilon\; \_\; \{1\}\; -\; \backslash \; varepsilon\; \_\; \{2\; \})\; ^\; \{2\}\; +\; (\backslash \; varepsilon\; \_\; \{2\}\; -\; \backslash \; varepsilon\; \_\; \{3\})\; ^\; \{2\}\; +\; (\backslash \; varepsilon\; \_\; \{3\}\; -\; \backslash \; varepsilon\; \_\; \{1\})\; ^\; \{2\}\}\}\}$

где $\epsilon \; 1,\; \epsilon \; 2,\; \epsilon \; 3\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{1\},\; \backslash \; varepsilon\; \_\; \{2\},\; \backslash \; varepsilon\; \_\; \{3\}\}$являются основными деформациями.

Нормальная деформация на октаэдрической плоскости определяется как

$\epsilon \; oct\; =\; 1\; 3\; (\epsilon \; 1\; +\; \epsilon \; 2\; +\; \epsilon \; 3)\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{\backslash \; mathrm\; \{oct\}\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{3\}\}\; (\backslash \; varepsilon\; \_\; \{1\}\; +\; \backslash \; varepsilon\; \_\; \{2\}\; +\; \backslash \; varepsilon\; \_\; \{3\})\}$

Эквивалентная деформация

Скалярная величина, называемая эквивалентной деформацией или эквивалентной деформацией по Мизесу, часто используется для описания состояния деформации в твердых телах. В литературе можно найти несколько определений эквивалентной деформации. Определение, которое обычно используется в литературе по пластичности :

$\epsilon \; e\; q\; =\; 2\; 3\; \epsilon \; d\; e\; v:\; \epsilon \; d\; e\; v\; =\; 2\; 3\; \epsilon \; i\; j\; d\; e\; v\; \epsilon \; i\; j\; d\; e\; v;\; \epsilon \; dev\; =\; \epsilon \; -\; 1\; 3\; тр\; (\epsilon )\; I\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{\backslash \; mathrm\; \{eq\}\}\; =\; \{\backslash \; sqrt\; \{\{\backslash \; tfrac\; \{2\}\; \{3\}\}\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; ^\; \{\; \backslash \; mathrm\; \{dev\}\}:\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; ^\; \{\backslash \; mathrm\; \{dev\}\}\}\; =\; \{\backslash \; sqrt\; \{\{\backslash \; tfrac\; \{2\}\; \{3\}\}\; \backslash \; varepsilon\; \_\; \{ij\}\; ^\; \{\backslash \; mathrm\; \{dev\}\}\; \backslash \; varepsilon\; \_\; \{ij\}\; ^\; \{\backslash \; mathrm\; \{dev\}\}\}\; ~;\; ~~\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; ^\; \{\backslash \; mathrm\; \{dev\}\}\; =\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; -\; \{\backslash \; tfrac\; \{1\}\; \{3\}\}\; \backslash \; mathrm\; \{tr\}\; (\{\backslash \; boldsymbol\; \{\backslash \; varepsilon\; \}\})\; ~\; \{\backslash \; boldsymbol\; \{I\}\}\}$

Эта величина является работой, сопряженной с эквивалентным напряжением, определенным как

$\sigma \; eq\; =\; 3\; 2\; \sigma \; dev:\; \sigma \; dev\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{\backslash \; mathrm\; \{\; eq\}\}\; =\; \{\backslash \; sqrt\; \{\{\backslash \; tfrac\; \{3\}\; \{2\}\}\; \{\backslash \; boldsymbol\; \{\backslash \; sigma\}\}\; ^\; \{\backslash \; mathrm\; \{dev\}\}:\; \{\backslash \; boldsymbol\; \{\backslash \; sigma\}\}\; ^\; \{\backslash \; mathrm\; \{dev\}\; \}\}\}$

Для заданных компонентов деформации $\epsilon \; ij\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{ij\}\}$уравнение тензора деформации $ui,\; j\; +\; uj,\; i\; =\; 2\; \epsilon \; ij\; \{\backslash \; displaystyle\; u\_\; \{i,\; j\}\; +\; u\_\; \{j,\; i\}\; =\; 2\; \backslash \; varepsilon\; \_\; \{ij\}\}$представляет собой систему шести дифференциальных уравнений для определения три компонента смещения $ui\; \{\backslash \; displaystyle\; u\_\; \{i\}\}$, что дает переопределенную систему. Таким образом, решение для произвольного выбора компонентов деформации обычно не существует. Поэтому на компоненты деформации накладываются некоторые ограничения, называемые уравнениями совместимости. С добавлением трех уравнений совместимости количество независимых уравнений сокращается до трех, что соответствует количеству неизвестных компонентов смещения. Эти ограничения на тензор деформации были обнаружены Сен-Венаном и названы «уравнениями совместимости Сен-Венана ».

Функции совместимости служат для обеспечения однозначной функции непрерывного смещения $u\; i\; \{\backslash \; displaystyle\; u\_\; \{i\}\}$. Если упругая среда визуализируется как набор бесконечно малых кубиков в недеформированном состоянии, после того, как среда деформирована, произвольный тензор деформации может не привести к ситуации, в которой искаженные кубы все еще подходят друг к другу без перекрытия.

В индексных обозначениях уравнения совместимости выражаются как

$\epsilon \; ij,\; km\; +\; \epsilon \; km,\; ij\; -\; \epsilon \; ik,\; jm\; -\; \epsilon \; jm,\; ik\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{ij,\; km\; \}\; +\; \backslash \; varepsilon\; \_\; \{km,\; ij\}\; -\; \backslash \; varepsilon\; \_\; \{ik,\; jm\}\; -\; \backslash \; varepsilon\; \_\; \{jm,\; ik\}\; =\; 0\}$

Инженерное обозначение

$\partial \; 2\; ϵ\; x\; \partial \; y\; 2\; +\; \partial \; 2\; ϵ\; y\; \partial \; Икс\; 2\; знак\; равно\; 2\; \partial \; 2\; ϵ\; xy\; \partial \; x\; \partial \; Y\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; epsilon\; \_\; \{x\}\}\; \{\backslash \; partial\; y\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; частичное\; ^\; \{2\}\; \backslash \; epsilon\; \_\; \{y\}\}\; \{\backslash \; partial\; x\; ^\; \{2\}\}\}\; =\; 2\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; epsilon\; \_\; \{xy\}\}\; \{\backslash \; partial\; x\; \backslash \; partial\; y\}\}\; \}$ $\partial \; 2\; ϵ\; y\; \partial \; z\; 2\; +\; \partial \; 2\; ϵ\; z\; \partial \; y\; 2\; =\; 2\; \partial \; 2\; ϵ\; yz\; \partial \; y\; \partial \; z\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; epsilon\; \_\; \{y\}\}\; \{\; \backslash \; partial\; z\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; epsilon\; \_\; \{z\}\}\; \{\backslash \; partial\; y\; ^\; \{2\}\}\}\; =\; 2\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; эпсилон\; \_\; \{yz\}\}\; \{\backslash \; partial\; y\; \backslash \; partial\; z\}\}\}$ $\partial \; 2\; ϵ\; x\; \partial \; z\; 2\; +\; \partial \; 2\; ϵ\; z\; \partial \; x\; 2\; =\; 2\; \partial \; 2\; ϵ\; zx\; \partial \; z\; \partial \; x\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; epsilon\; \_\; \{x\}\}\; \{\backslash \; partial\; z\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; epsilon\; \_\; \{z\}\}\; \{\backslash \; partial\; x\; ^\; \{2\}\; \}\}\; =\; 2\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; epsilon\; \_\; \{zx\}\}\; \{\backslash \; par\; tial\; z\; \backslash \; partial\; x\}\}\}$ $\partial \; 2\; ϵ\; x\; \partial \; y\; \partial \; z\; =\; \partial \; \partial \; x\; (-\; \partial \; ϵ\; yz\; \partial \; x\; +\; \partial \; ϵ\; zx\; \partial \; y\; +\; \partial \; ϵ\; ху\; \partial \; Z)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\; \backslash \; partial\; ^\; \{2\}\; \backslash \; epsilon\; \_\; \{x\}\}\; \{\backslash \; partial\; y\; \backslash \; partial\; z\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; x\}\}\; \backslash \; left\; (-\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; epsilon\; \_\; \{\; yz\}\}\; \{\backslash \; partial\; x\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; epsilon\; \_\; \{zx\}\}\; \{\backslash \; partial\; y\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; epsilon\; \_\; \{xy\}\}\; \{\backslash \; partial\; z\}\}\; \backslash \; справа)\}$ $\partial \; 2\; ϵ\; y\; \partial \; z\; \partial \; x\; =\; \partial \; \partial \; y\; (\partial \; ϵ\; yz\; \partial \; x\; -\; \partial \; ϵ\; zx\; \partial \; y\; +\; \partial \; ϵ\; xy\; \partial \; z)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; epsilon\; \_\; \{y\}\}\; \{\backslash \; partial\; z\; \backslash \; partial\; x\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; y\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; \backslash \; epsilon\; \_\; \{yz\}\}\; \{\backslash \; partial\; x\; \}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; epsilon\; \_\; \{zx\}\}\; \{\backslash \; partial\; y\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; epsilon\; \_\; \{xy\}\}\; \{\backslash \; partial\; z\}\}\; \backslash \; right)\}$ $\partial \; 2\; ϵ\; z\; \partial \; x\; \partial \; y\; знак\; равно\; \partial \; \partial \; z\; (\partial \; ϵ\; yz\; \partial \; x\; +\; \partial \; ϵ\; zx\; \partial \; y\; -\; \partial \; ϵ\; xy\; \partial \; z)\; \{\backslash \; displaystyle\; \{\backslash \; fr\; ac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; epsilon\; \_\; \{z\}\; \}\; \{\backslash \; partial\; x\; \backslash \; partial\; y\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; z\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; \backslash \; epsilon\; \_\; \{yz\}\}\; \{\; \backslash \; partial\; x\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; epsilon\; \_\; \{zx\}\}\; \{\backslash \; partial\; y\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; epsilon\; \_\; \{xy\}\}\; \{\backslash \; partial\; z\}\}\; \backslash \; right)\}$

Плоская деформация

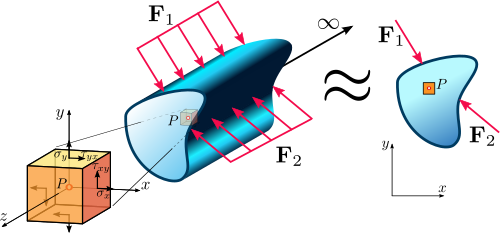
Плоское деформированное состояние в континууме.

В реальных инженерных компонентах напряжение (и деформация) равны 3- D тензоры, но в призматических структурах, таких как длинная металлическая заготовка, длина структуры намного больше, чем два других измерения. Деформации, связанные с длиной, т.е. нормальная деформация $\epsilon \; 33\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{33\}\}$и деформации сдвига $\epsilon \; 13\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{13\}\}$и $\epsilon \; 23\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{23\}\}$(если длина - 3 направления) ограничены близкими инструментами и малы по сравнению с поперечными деформациями. В таком случае плоская деформация является приемлемым приближением. тензор деформации для плоской деформации записывается как:

$\epsilon \; \_\; \_\; =\; [\epsilon \; 11\; \epsilon \; 12\; 0\; \epsilon \; 21\; \epsilon \; 22\; 0\; 0\; 0\; 0]\; \{\backslash \; displaystyle\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; boldsymbol)\; \{\; \backslash \; varepsilon\}\}\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; varepsilon\; \_\; \{11\}\; \backslash \; varepsilon\; \_\; \{12\}\; 0\; \backslash \backslash \backslash \; varepsilon\; \_\; \{21\}\; \backslash \; varepsilon\; \_\; \{22\}\; 0\; \backslash \backslash \; 0\; 0\; 0\; \backslash \; end\; \{bmatrix\}\}\}$

, в котором двойное подчеркивание обозначает тензор второго порядка. Это деформированное состояние называется плоской деформацией. Соответствующий тензор напряжений:

$\sigma \; \_\; \_\; =\; [\sigma \; 11\; \sigma \; 12\; 0\; \sigma \; 21\; \sigma \; 22\; 0\; 0\; 0\; \sigma \; 33]\; \{\backslash \; displaystyle\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; boldsymbol\; \{\backslash \; sigma\}\}\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; sigma\; \_\; \{11\}\; \backslash \; sigma\; \_\; \{12\}\; 0\; \backslash \backslash \backslash \; sigma\; \_\; \{21\}\; \backslash \; sigma\; \_\; \{22\}\; 0\; \backslash \backslash \; 0\; 0\; \backslash \; sigma\; \_\; \{33\}\; \backslash \; end\; \{\; bmatrix\}\}\}$

, в котором ненулевое значение $\sigma \; 33\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{33\}\}$необходимо для поддержания ограничения $ϵ\; 33\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; epsilon\; \_\; \{33\}\; =\; 0\}$. Этот термин напряжения может быть временно удален из анальной проблемы.

Антиплоскостная деформация

Антиплоскостная деформация - это другое особое состояние деформации, которое может возникнуть в теле, например, в области, близкой к винтовой дислокации. тензор деформации для деформации антиплоскости определяется как

$\epsilon \; \_\; \_\; =\; [0\; 0\; \epsilon \; 13\; 0\; 0\; \epsilon \; 23\; \epsilon \; 13\; \epsilon \; 23\; 0]\; \{\backslash \; displaystyle\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon))\}\}\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; 0\; \backslash \; varepsilon\; \_\; \{13\}\; \backslash \backslash \; 0\; 0\; \backslash \; varepsilon\; \_\; \{23\}\; \backslash \backslash \backslash \; varepsilon\; \_\; \{13\}\; \backslash \; varepsilon\; \_\; \{23\}\; 0\; \backslash \; end\; \{bmatrix\}\}\}$

Тензор бесконечно малых деформаций определяется как

$\epsilon \; =\; 1\; 2\; [\nabla \; u\; +\; (\nabla \; u)\; T]\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; [\{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; mathbf\; \{u\}\; +\; (\{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; mathbf\; \{u\})\; ^\; \{T\}\; ]\}$

Таким образом градиент с территории может быть выражен как

$\nabla \; u\; =\; \epsilon \; +\; \omega \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; mathbf\; \{u\}\; =\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; +\; \{\; \backslash \; boldsymbol\; \{\backslash \; omega\}\}\}$

где

$\omega :\; =\; 1\; 2\; [\nabla \; u\; -\; (\nabla \; u)\; T]\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}:\; =\; \{\backslash \; frac\; \{1\}\; \{\; 2\}\}\; [\{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; mathbf\; \{u\}\; -\; (\{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; mathbf\; \{u\; \})\; ^\; \{T\}]\}$

Количество $\omega \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\}$- это тензор бесконечно малого вращения . Этот тензор кососимметричен. Для бесконечно малых деформаций скалярные компоненты $\omega \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\}$удовлетворяют условию $|\; \omega \; i\; j\; |\; \ll \; 1\; \{\backslash \; displaystyle\; |\; \backslash \; omega\; \_\; \{ij\}\; |\; \backslash \; ll\; 1\}$. Обратите внимание, что градиент с повреждением мал только в том случае, если и тензор деформации и тензор вращения бесконечно малы.

Осевой вектор

Кососимметричный тензор второго порядка имеет три независимых скалярных компонента. Эти три компонента используются для определения аксиального вектора, $w\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{w\}\}$, как показано ниже:

$\omega \; i\; j\; =\; -\; ϵ\; i\; j\; k\; w\; k;\; wi\; знак\; равно\; -\; 1\; 2\; ϵ\; ijk\; \omega \; jk\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{ij\}\; =\; -\; \backslash \; epsilon\; \_\; \{ijk\}\; ~\; w\_\; \{k\}\; ~;\; ~~\; w\_\; \{i\}\; =\; -\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; ~\; \backslash \; epsilon\; \_\; \{ijk\}\; ~\; \backslash \; omega\; \_\; \{jk\}\}$

где $ϵ\; ijk\; \{\backslash \; displaystyle\; \backslash \; epsilon\; \_\; \{ijk\; \}\}$- символ перестановки . В матричной форме

$\omega \; \_\; \_\; =\; [0\; -\; w\; 3\; w\; 2\; w\; 3\; 0\; -\; w\; 1\; -\; w\; 2\; w\; 1\; 0];\; вес\; \_\; =\; [вес\; 1\; вес\; 2\; вес\; 3]\; \{\backslash \; displaystyle\; \{\backslash \; underline\; \{\backslash \; underline\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; -w\_\; \{3\}\; w\_\; \{2\}\; \backslash \; \backslash \; w\_\; \{3\}\; 0\; -w\_\; \{1\}\; \backslash \backslash \; -\; w\_\; \{2\}\; w\_\; \{1\}\; 0\; \backslash \; end\; \{bmatrix\}\}\; ~;\; ~~\; \{\backslash \; underline\; \{\backslash \; mathbf\; \{w\}\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; w\_\; \{1\}\; \backslash \backslash \; w\_\; \{2\}\; \backslash \backslash \; w\_\; \{3\}\; \backslash \; end\; \{bmatrix\}\}\}$

Осевой вектор также называется бесконечно малым вектором вращения . Вектор вращения связан с градиентом с нарушением воздействия

$w\; =\; 1\; 2\; \nabla \; \times \; u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{w\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; ~\; \{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; times\; \backslash \; mathbf\; \{\; u\}\}$

В индексной записи

$wi\; =\; 1\; 2\; ϵ\; ijkuk,\; j\; \{\backslash \; displaystyle\; w\_\; \{i\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; ~\; \backslash \; epsilon\; \_\; \{ijk\}\; ~\; u\_\; \{k,\; j\}\}$

Если $\Vert \; \omega \; \Vert \; \ll \; 1\; \{\backslash \; displaystyle\; \backslash \; lVert\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\; \backslash \; rVert\; \backslash \; ll\; 1\}$и $\epsilon \; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; =\; \{\backslash \; boldsymbol\; \{0\}\}\}$, то твердое тело вращается на $|\; w\; |\; \{\backslash \; displaystyle\; |\; \backslash \; mathbf\; \{w\}\; |\}$вокруг вектора $w\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{w\}\}$.

Связь между тензором деформации и вектором вращения

Дано непрерывное однозначное поле с ущербом $u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\}$и соответствующие тензор бесконечно малых деформаций $\epsilon \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\}$, имеем (см Тензорная производная (механика сплошной среды) )

$\nabla \; \times \; \epsilon \; =\; eijk\; \epsilon \; lj,\; iek\; \otimes \; el\; =\; 1\; 2\; eijk\; [ul,\; ji\; +\; uj,\; li]\; ek\; \otimes \; эль\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; nabla\; \}\}\; \backslash \; times\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; =\; e\_\; \{ijk\}\; ~\; \backslash \; varepsilon\; \_\; \{lj,\; i\}\; ~\; \backslash \; mathbf\; \{e\}\; \_\; \{k\}\; \backslash \; otimes\; \backslash \; mathbf\; \{e\}\; \_\; \{l\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; ~\; e\_\; \{ijk\}\; ~\; [u\_\; \{l,\; ji\}\; +\; u\_\; \{j,\; li\}]\; ~\; \backslash \; mathbf\; \{e\}\; \_\; \{k\}\; \backslash \; otimes\; \backslash \; mathbf\; \{e\}\; \_\; \{l\}\; \}$

Временное изменение порядка дифференцирования не меняет результат, $ul,\; ji\; =\; ul,\; ij\; \{\backslash \; displaystyle\; u\_\; \{l,\; ji\}\; =\; u\_\; \{l,\; ij\}\}$. Следовательно,

$eijkul,\; ji\; =\; (e\; 12\; k\; +\; e\; 21\; k)\; ul,\; 12\; +\; (e\; 13\; k\; +\; e\; 31\; k)\; ul,\; 13\; +\; (\; е\; 23\; к\; +\; е\; 32\; к)\; ul,\; 32\; =\; 0\; \{\backslash \; displaystyle\; \backslash ,\; e\_\; \{ijk\}\; u\_\; \{l,\; ji\}\; =\; (e\_\; \{12k\}\; +\; e\_\; \{21k\})\; u\_\; \{l,\; 12\}\; +\; (e\_\; \{\; 13k\}\; +\; e\_\; \{31k\})\; u\_\; \{l,\; 13\}\; +\; (e\_\; \{23k\}\; +\; e\_\; \{32k\})\; u\_\; \{l,\; 32\}\; =\; 0\}$

Также

$1\; 2\; eijkuj,\; li\; =\; (1\; 2\; eijkuj,\; i),\; l\; =\; (1\; 2\; ekijuj,\; i),\; l\; =\; wk,\; l\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; ~\; e\_\; \{ijk\}\; ~\; u\_\; \{j,\; li\}\; =\; \backslash \; left\; (\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; ~\; e\_\; \{ijk\}\; ~\; u\_\; \{j,\; i\}\; \backslash \; right)\; \_\; \{,\; l\}\; =\; \backslash \; left\; (\{\backslash \; tfrac\; \{1\}\; \{2\}\}\; ~\; e\_\; \{kij\}\; ~\; u\_\; \{j,\; i\}\; \backslash \; right)\; \_\; \{,\; l\}\; =\; w\_\; \{k,\; l\}\}$

Следовательно,

$\nabla \; \times \; \epsilon \; =\; wk,\; lek\; \otimes \; el\; =\; \nabla \; w\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; times\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; =\; w\_\; \{k,\; l\}\; ~\; \backslash \; mathbf\; \{e\}\; \_\; \{k\}\; \backslash \; otimes\; \backslash \; mathbf\; \{e\}\; \_\; \{l\}\; =\; \{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; mathbf\; \{w\}\}$

Связь между тензором и вектором вращения

Из важного тождества, касающегося curl тензора, мы знаем, что для непрерывного одиночного -значного поля с $и\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\}$,

$\nabla \; \times \; (\nabla \; u)\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; times\; (\{\; \backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; mathbf\; \{u\})\; =\; \{\backslash \; boldsymbol\; \{0\}\}.\}$

Времен $\nabla \; u\; =\; \epsilon \; +\; \omega \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; mathbf\; \{\; u\}\; =\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; +\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\}$мы имеем $\nabla \; \times \; \omega \; =\; -\; \nabla \; \times \; \epsilon \; =\; -\; ш.\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; times\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\; =\; -\; \{\backslash \; boldsymbol\; \{\backslash \; nabla\}\}\; \backslash \; times\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; =\; -\; \{\backslash \; boldsymbol\; \{\backslash \; nabla\}\; \}\; \backslash \; mathbf\; \{w\}.\}$

В цилиндрических полярных координат ($r,\; \theta ,\; z\; \{\backslash \; displaystyle\; r,\; \backslash \; theta,\; z\; \}$) вектор с ущерба можно записать как

$u\; =\; urer\; +\; u\; \theta \; e\; \theta \; +\; uzez\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\; =\; u\_\; \{r\}\; ~\; \backslash \; mathbf\; \{e\}\; \_\; \{r\}\; +\; u\; \_\; \{\backslash \; theta\}\; ~\; \backslash \; mathbf\; \{e\}\; \_\; \{\backslash \; theta\}\; +\; u\_\; \{z\}\; ~\; \backslash \; mathbf\; \{e\}\; \_\; \{z\}\}$

Компоненты тензора деформации в цилиндрической системе координат задается по формуле: $ε rr = ∂ ur ∂ r ε θ θ = 1 r (∂ u θ ∂ θ + ur) ε zz = ∂ uz ∂ z ε r θ = 1 2 (1 r ∂ ur ∂ θ + ∂ u θ ∂ r - u θ r) ε θ z знак равно 1 2 (∂ u θ ∂ z + 1 r ∂ uz ∂ θ) ε zr = 1 2 (∂ ur ∂ z + ∂ uz ∂ r) {\ displaystyle {\ начало {выровнено} \ varepsilon _ {rr} = {\ cfrac {\ partial u_ {r}} {\ partial r}} \\\ varepsilon _ {\ theta \ theta} = {\ cfrac {1} {r}} \ слева ({\ cfrac {\ partial u _ {\ theta}} {\ partial \ theta}} + u_ {r} \ right) \\\ varepsilon _ {zz} = {\ cfrac {\ partial u_ {z} } {\ partial z}} \\\ varepsilon _ {r \ theta} = {\ cfrac {1} {2}} \ left ({\ cfrac {1} {r}} {\ cfrac {\ partial u_ { r}} {\ partial \ theta}} + {\ cfrac {\ partial u _ {\ theta}} {\ partial r}} - {\ cfrac {u _ {\ theta}} {r}} \ right) \ \\ varepsilon _ {\ theta z} = {\ cfrac {1} {2}} \ left ({\ cfrac {\ частичное u _ {\ theta}} {\ partial z}} + {\ cfrac {1} {r}} {\ cfrac {\ partial u_ {z}} {\ partial \ theta}} \ right) \\\ varepsilon _ {zr} = {\ cfrac {1} {2}} \ left ({\ cfrac {\ partial u_ {r}} {\ partial z}} + {\ cfrac {\ partial u_ {z}} {\ partial r}} \ right) \ end {align}}}$

В сферических координатах ($r,\; \theta ,\; \varphi \; \{\backslash \; displaystyle\; r,\; \backslash \; theta,\; \backslash \; phi\}$), вектор с ущерба можно записать как

Сферические координаты (r, θ, φ), обычно используемые в физике: радиал ьное расстояние r, полярный угол θ (theta ) и азимутальный угол φ (phi ). Символ ρ (rho ) часто используется вместо r.

$u\; =\; urer\; +\; u\; \theta \; e\; \theta \; +\; u\; \varphi \; e\; \varphi \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\; =\; u\_\; \{r\}\; ~\; \backslash \; mathbf\; \{e\}\; \_\; \{r\}\; +\; u\; \_\; \{\backslash \; theta\}\; ~\; \backslash \; mathbf\; \{\; e\}\; \_\; \{\backslash \; theta\}\; +\; u\; \_\; \{\backslash \; phi\}\; ~\; \backslash \; mathbf\; \{e\}\; \_\; \{\backslash \; phi\}\}$

Компоненты тензор деформации в сферической системе координат задается выражением

$ε rr = ∂ ur ∂ r ε θ θ = 1 r (∂ u θ ∂ θ + ur) ε ϕ ϕ = 1 r sin ⁡ θ (∂ u ϕ ∂ ϕ + ur sin ⁡ θ + u θ cos ⁡ θ) ε r θ = 1 2 (1 r ∂ ur ∂ θ + ∂ u θ ∂ r - u θ r) ε θ ϕ = 1 2 r (1 sin ⁡ θ ∂ u θ ∂ ϕ + ∂ u ϕ ∂ θ - u ϕ раскладушка ⁡ θ) ε ϕ r = 1 2 (1 р грех ⁡ θ ∂ ur ∂ ϕ + ∂ u ϕ ∂ r - u ϕ r) {\ displaystyle {\ begin {выровнено} \ varepsilon _ {rr} = {\ cfrac {\ partial u_ {r}} { \ partial r}} \\\ varepsilon _ {\ theta \ theta} = {\ cfrac {1} {r}} \ left ({\ cfrac {\ partial u _ {\ theta}} {\ partial \ theta} } + u_ {r} \ right) \\\ varepsilon _ {\ phi \ phi} = {\ cfrac {1} {r \ sin \ theta}} \ left ({\ cfrac {\ partial u _ {\ phi }} {\ partial \ phi}} + u_ {r} \ sin \ theta + u _ {\ theta} \ cos \ theta \ right) \\\ varepsilon _ {r \ theta} = {\ cfrac {1} {2}} \ left ({\ cfra c {1} {r}} {\ cfrac {\ partial u_ {r}} {\ partial \ theta}} + {\ cfrac {\ partial u _ {\ theta}} {\ partial r}} - {\ cfrac {u _ {\ theta}} {r}} \ right) \\\ varepsilon _ {\ theta \ phi} = {\ cfrac {1} {2r}} \ left ({\ cfrac {1} {\ sin \ theta}} {\ cfrac {\ partial u _ {\ theta}} {\ partial \ phi}} + {\ cfrac {\ частичный u _ {\ phi}} {\ partial \ theta}} - u _ {\ phi} \ cot \ theta \ right) \\\ varepsilon _ {\ phi r} = {\ cfrac {1} {2} } \ left ({\ cfrac {1} {r \ sin \ theta}} {\ cfrac {\ partial u_ {r}} {\ partial \ phi}} + {\ cfrac {\ partial u _ {\ phi}} {\ partial r}} - {\ cfrac {u _ {\ phi}} {r}} \ right) \ end {выровнено}}}$

• Деформация (механика)
• Совместимость (механика)
• Напряжение
• Тензодатчик
• Кривая напряжение-деформации
• Закон Гука
• Коэффициент Пуассона
• Теория конечных деформаций
• Скорость деформации
• Плоское напряжение
• Корреляция цифровых изображений