Циклид Дюпена

редактировать

Циклид Дюпена

В математике Циклид Дюпена или Циклид Дюпена - это любая геометрическая инверсия стандартного тора , цилиндра или двойного конуса. В частности, последние сами являются примерами циклидов Дюпена. Они были обнаружены (и названы в честь) Шарлем Дюпеном в его диссертации 1803 года под заголовком Гаспар Монж. Ключевым свойством циклида Дюпена является то, что он представляет собой поверхность канала (огибающая однопараметрического семейства сфер) двумя разными способами. Это свойство означает, что циклиды Дюпена являются естественными объектами в геометрии сферы Ли.

Циклиды Дюпена часто называют просто циклидами, но последний термин также используется для обозначения более общего класса поверхностей четвертой степени которые важны в теории разделения переменных для уравнения Лапласа в трех измерениях.

Циклиды Дюпена исследовал не только Дюпен, но и А. Кэли, Дж. К. Максвелл и Мейбл М. Янг.

Циклиды Дюпена используются в автоматизированном проектировании, потому что циклидные пластыри имеют рациональное представление и подходят для смешивания поверхностей каналов (цилиндры, конусы, торы, и другие).

Содержание

1 Определения и свойства
2 Параметрическое и неявное представление
- 2.1 Эллиптические циклиды
- 2.2 Параболические циклиды
3 Циклид как поверхность канала
- 3.1 Эллипс как направляющая
- 3.2 Свойство Максвелла
- 3.3 Циклид через 4 точки на оси x
- 3.4 Параллельные поверхности
- 3.5 Гипербола как директриса
- 3.6 Свойство Максвелла (случай гиперболы)
- 3.7 Вывод параметрического представления
  - 3.7.1 Эллиптический циклид
  - 3.7.2 Параболический циклид
4 Циклиды Дюпена и геометрические инверсии
- 4.1 Пример цилиндра
- 4.2 Пример конуса
- 4.3 Пример тора
5 Разделение переменных
6 См. Также
7 Примечания
8 Ссылки
9 Внешние ссылки

Определения и свойства

Существует несколько эквивалентных определений циклидов Дюпена. В $R 3 {\ displaystyle \ mathbb {R} ^ {3}}$ $\mathbb{R} ^{3}$ они могут быть определены как изображения при любой инверсии торов, цилиндров и двойных конусов. Это показывает, что класс циклид Дюпена инвариантен относительно преобразований Мёбиуса (или конформных). В сложном пространстве $C 3 {\ displaystyle \ mathbb {C} ^ {3}}$ $\mathbb {C} ^{3}$ эти три последних разновидности могут быть сопоставлены друг с другом путем инверсии, поэтому циклиды Дюпена могут быть определены как инверсии тор (или цилиндр, или двойной конус).

Поскольку стандартный тор - это орбита точки под двумерной абелевой подгруппой группы Мёбиуса, отсюда следует, что циклиды также являются орбитой, и это обеспечивает второй способ их определения.

Третье свойство, которое характеризует циклиды Дюпена, состоит в том, что их линии кривизны представляют собой все круги (возможно, через точку на бесконечности ). Эквивалентно, сферы , касательные к поверхности с радиусами, равными обратным основным кривизнам в точке касания, постоянны вдоль соответствующие линии кривизны: это касательные сферы, содержащие соответствующие линии кривизны в виде больших окружностей. Аналогично, оба листа фокальной поверхности вырождаются в конические формы. Отсюда следует, что любой циклид Дюпена является поверхностью канала (т.е. огибающей однопараметрического семейства сфер) двумя различными способами, и это дает другую характеристику.

Определение в терминах сфер показывает, что класс циклидов Дюпена инвариантен относительно большей группы всех преобразований сфер Ли ; любые два циклида Дюпена эквивалентны Ли. Они образуют (в некотором смысле) простейший класс инвариантных относительно Ли поверхностей после сфер и поэтому особенно важны в геометрии сфер Ли.

Определение также означает, что циклид Дюпена является огибающей однопараметрического семейство сфер, касающихся трех заданных взаимно касательных сфер. Отсюда следует, что он касается бесконечного множества конфигураций сфер гекслета Содди.

Параметрическое и неявное представление

(CS): Циклид Дюпена может быть представлен двумя способами как огибающая однопараметрического пучка сфер, т.е. поверхность канала с двумя направляющими . Пара направляющих представляет собой фокальные коники и состоит либо из эллипса и гиперболы, либо из двух парабол. В первом случае циклид определяется как эллиптический, во втором - как параболический. В обоих случаях коники содержатся в двух взаимно ортогональных плоскостях. В крайних случаях (если эллипс представляет собой круг) гипербола вырождается в линию, а циклид - это тор вращения.

Еще одно специальное свойство циклида:

(CL): Любое линия кривизны циклида Дюпена представляет собой окружность.

Эллиптические циклиды

Эллиптические циклиды можно параметрически представить следующими формулами (см. Раздел Циклид как поверхность канала):

Значения проектных параметров

a, b, c, d {\ displaystyle a, b, c, d}

a,b,c,d

d {\ displaystyle d}

d

- радиус порождающая сфера в совпадающих вершинах эллипса. Две окружности на плоскости xz с центрами

(± a, 0, 0) {\ displaystyle (\ pm a, 0,0)}

(\pm a,0,0)

имеют радиусы

d ∓ c {\ displaystyle d \ mp c}

d\mp c

.. Здесь:

a = 1, b = 0,98 → c = 0,199 {\ displaystyle a = 1, \; b = 0,98 \ to c = 0,199}

a=1,\;b=0.98\to c=0.199

d = 0,3 {\ displaystyle d = 0,3}

d=0.3

x = d (c - a cos ⁡ u cos ⁡ v) + b 2 cos ⁡ ua - с соз ⁡ U соз ⁡ v, {\ displaystyle x = {\ frac {d (ca \ cos u \ cos v) + b ^ {2} \ cos u} {ac \ cos u \ cos v}} \,}

x=\frac{d(c-a\cos u\cos v)+b^2\cos u}{a-c\cos u \cos v} \,

y = b sin ⁡ u (a - d cos ⁡ v) a - c cos ⁡ u соз ⁡ v, {\ displaystyle y = {\ frac {b \ sin u (ad \ cos v)} {ac \ cos u \ cos v}} \,}

y=\frac{b\sin u (a-d\cos v)}{a-c\cos u \cos v} \,

z = b sin ⁡ v (c cos ⁡ u - d)) a - c соз ⁡ u соз ⁡ v, {\ displaystyle z = {\ frac {b \ sin v (c \ cos ud))} {ac \ cos u \ cos v}} \,}

z=\frac{b\sin v (c \cos u-d))}{a-c\cos u \cos v} \,

0 ≤ u, v < 2 π. {\displaystyle 0\leq u,v<2\pi \.}

0\le u,v <2\pi \.

Числа $a, b, c, d {\ displaystyle a, b, c, d}$ $a,b,c,d$ представляют собой большую и малую полуоси и $c {\ displaystyle c}$ $c$ линейный эксцентриситет эллипса:

x 2 a 2 + y 2 b 2 = 1, z = 0. {\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 1, z = 0 \.}

{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,z=0\.

Гипербола $x 2 c 2 - z 2 b 2 = 1, y = 0 {\ displaystyle {\ frac {x ^ {2}} {c ^ {2}}} - {\ frac {z ^ {2}} {b ^ {2}}} = 1, y = 0}$ $\frac{x^2}{c^2}-\frac{z^2}{b^2}=1, y=0$ - фокальная коника эллипса. Это означает: фокусы / вершины эллипса - это вершины / фокусы гиперболы. Две коники образуют две вырожденные фокальные поверхности циклида.

$d {\ displaystyle d}$ $d$ можно рассматривать как средний радиус генерирующих сфер.

Для $u = const {\ displaystyle u = const}$ $u=const$ , $v = const {\ displaystyle v = const}$ $v=const$ соответственно, получаются линии (окружности) кривизны поверхность.

Соответствующее неявное представление :

(x 2 + y 2 + z 2 + b 2 - d 2) 2 - 4 (ax - cd) 2 - 4 b 2 у 2 = 0. {\ displaystyle (x ^ {2} + y ^ {2} + z ^ {2} + b ^ {2} -d ^ {2}) ^ {2} -4 (ax-cd) ^ {2} - 4b ^ {2} y ^ {2} = 0 \.}

(x^2+y^2+z^2+b^2-d^2)^2-4(ax-cd)^2-4b^2y^2=0 \.

В случае $a = b {\ displaystyle a = b}$ $a=b$ получается $c = 0 {\ displaystyle c = 0}$ $c=0$ , т.е. е. эллипс - это круг, а гипербола вырождается в прямую. Соответствующие циклиды - это торы вращения.

(эллипс.) Циклиды Дюпена для расчетных параметров a, b, c, d
$d = 0 {\ displaystyle d = 0}$ $d=0$	$0 < d < c {\displaystyle 0$ $0<d<c$	$d = c {\ displaystyle d = c}$ $d=c$	$c < d {\displaystyle c$ $c<d$	$d = a {\ displaystyle d = a}$ $d=a$	$a < d {\displaystyle a$ $a<d$

symm. рог циклид	рог циклид	рог циклид	кольцевой циклид	кольцевой циклид	шпиндельный циклид

точки пересечения циклида с осью абсцисс. См. Раздел Циклид через 4 точки на оси x.

Параболические циклиды

Параболический циклид может быть представлен следующим параметрическим представлением (см. Раздел Циклид как поверхность канала) :

параболический циклид с его направляющими (фокальные параболы)

x = p 2 2 v 2 + k (1 - u 2 - v 2) 1 + u 2 + v 2, {\ displaystyle x = {\ frac {p} {2}} \, {\ frac {2v ^ {2} + k (1-u ^ {2} -v ^ {2})} {1 + u ^ {2} + v ^ {2} }} \,}

x=\frac{p}{2}\, \frac{2v^2+k(1-u^2-v^2)}{1+u^2+v^2} \,

y = puv 2 + k 1 + u 2 + v 2, {\ displaystyle y = pu \, {\ frac {v ^ {2} + k} {1 + u ^ {2} + v ^ {2}}} \,}

y=pu\, \frac{v^2+k}{1+u^2+v^2} \,

z = pv 1 + u 2 - k 1 + u 2 + v 2, {\ displaystyle z = pv \, {\ frac {1 + u ^ {2} -k} {1 + u ^ {2} + v ^ {2}}} \,}

z=pv\, \frac{1+u^2-k}{1+u^2+v^2} \,

- ∞ < u, v < ∞. {\displaystyle -\infty

-\infty<u,v<\infty \.

Число $p {\ displaystyle p}$ $p$ определяет форму обеих парабол, которые являются фокальными кониками:

y 2 = p 2 - 2 px, z = 0 {\ displaystyle y ^ {2} = p ^ {2} -2px, \ z = 0 \}

y^{2}=p^{2}-2px,\ z=0\

z 2 = 2 пикселя, y = 0. {\ displaystyle \ z ^ {2} = 2px, \ y = 0 \.}

\ z^{2}=2px,\ y=0\.

$k {\ displaystyle k}$ $k$ определяет соотношение диаметров двух отверстий (см. диаграмму). $k = 0,5 {\ displaystyle k = 0,5}$ $k=0.5$ означает: оба диаметра равны. Для диаграммы $k = 0,7 {\ displaystyle k = 0,7}$ $k=0.7$ .

Соответствующее неявное представление

(x + (k 2-1) p) (x 2 + y 2 + z 2 - k 2 p 2 4) + pz 2 = 0. {\ displaystyle \ left (x + \ left ({\ frac {k} {2}} - 1 \ right) p \ right) \ left (x ^ {2} + y ^ {2} + z ^ {2} - {\ frac {k ^ {2} p ^ {2}} {4}} \ right) + pz ^ {2} = 0 \.}

\left(x+\left({\frac {k}{2}}-1\right)p\right)\left(x^{2}+y^{2}+z^{2}-{\frac {k^{2}p^{2}}{4}}\right)+pz^{2}=0\.

параболические циклиды Дюпена для расчетных параметров p = 1, k
$k = 0,5 {\ displaystyle k = 0,5}$ $k=0.5$	$k = 1 {\ displaystyle k = 1}$ $k=1$	$k = 1,5 {\ displaystyle k = 1,5}$ $k=1.5$

кольцевой циклид	рог циклида	рог циклида

Примечание: при отображении кружков появляются зазоры, которые вызваны необходимым ограничением параметров $u, v {\ displaystyle u, v}$ $u,v$ .

Циклид как поверхность канала

Циклид Дюпена как поверхность канала (оболочка семейства сфер)

Существует два способа создания эллиптического циклида Дюпена как поверхности канала . Первый использует эллипс в качестве директрисы, второй - гиперболу:

Эллипс в качестве директрисы

В плоскости xy директрисой является эллипс с уравнением

x 2 a 2 + y 2 b 2 = 1, z = 0 {\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 1 \, \ z = 0 \ quad}

{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\,\ z=0\quad

a>b {\ displaystyle \ a>b}

\ a>b

Он имеет параметрическое представление

x, = a cos ⁡ Y знак равно б грех ⁡ φ, Z знак равно 0, {\ Displaystyle \ х = а \ соз \ varphi \;, \ у = б \ грех \ varphi \;, \ z = 0 \.}

\ x=a\cos \varphi \;,\ y=b\sin \varphi \;,\ z=0\.

$а {\ Displaystyle a}$ $a$ - большая полуось, а $b {\ displaystyle b}$ $b$ - малая полуось. $c {\ displaystyle c}$ $c$ - линейный эксцентриситет эллипса. Отсюда: $c 2 = a 2 - b 2 {\ displaystyle c ^ {2} = a ^ {2} -b ^ {2}}$ $c^{2}=a^{2}-b^{2}$ . Радиусы производящие сферы:

r (φ) = d - c cos ⁡ φ. {\ displaystyle r (\ va rphi) = d-c \ cos \ varphi \.}

r(\varphi)=d-c\cos \varphi \.

$d {\ displaystyle d}$ $d$ - параметр проекта. Его можно рассматривать как среднее значение радиусов сфер. В случае $c = 0 {\ displaystyle c = 0}$ $c=0$ эллипс представляет собой круг, а циклид - тор вращения с $d {\ displaystyle d}$ $d$ радиус образующей окружности (образующей).

На диаграмме: $a = 1, b = 0,99, d = 0,25 {\ displaystyle \; a = 1, \; b = 0,99, \ d = 0,25 \;}$ $\;a=1,\;b=0.99,\ d=0.25\;$ .

Максвелл : Свойство фокусов эллипса директрис. Эллипс - это эквидистантный набор синих и фиолетовых кругов.

Свойство Максвелла

Следующее простое соотношение между фактическим центром сферы (точкой эллипса) и соответствующим радиусом сферы обусловлено Максвеллу:

Разница / сумма радиуса сферы и расстояния центра сферы (точки эллипса) от одного (но фиксированного) фокусов постоянна.

Доказательство

Фокусы эллипса $E = (a соз φ, b sin ⁡ φ, 0) {\ displaystyle \ E = (a \ cos \ varphi, b \ sin \ varphi, 0) \}$ $\ E=(a\cos \varphi,b\sin \varphi,0)\$ являются $F я знак равно (± с, 0, 0) {\ displaystyle \ F_ {i} = (\ pm c, 0,0) \}$ $\ F_{i}=(\pm c,0,0)\$ . Если выбрать $F 1 = (c, 0, 0) {\ displaystyle \ F_ {1} = (c, 0,0) \}$ $\ F_{1}=(c,0,0)\$ и вычислить расстояние $| E F 1 | {\ displaystyle \ | EF_ {1} | \}$ $\ |EF_{1}|\$ , получается $| E F 1 | знак равно а - с соз ⁡ φ {\ Displaystyle \ | EF_ {1} | = а-с \ соз \ varphi \}$ $\ |EF_{1}|=a-c\cos \varphi \$ . Вместе с радиусом реальной сферы (см. Выше) получаем $| E F 1 | - r = a - d {\ displaystyle \ | EF_ {1} | -r = a-d \}$ $\ |EF_{1}|-r=a-d\$ .. Выбор другого фокуса дает: $| E F 2 | + г = а + д. {\ displaystyle \ | EF_ {2} | + r = a + d \.}$ $\ |EF_{2}|+r=a+d\.$

Следовательно:

В плоскости xy огибающие окружностей сфер представляют собой две окружности с фокусами эллипс в качестве центров и радиусы $a ± d {\ displaystyle a \ pm d}$ $a\pm d$ (см. диаграмму).

Циклид через 4 точки на оси x

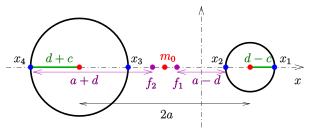
Определение проектных параметров a, b, c, d, принадлежащих заданным реалам

x 1, x 2, x 3, x 4 {\ displaystyle x_ {1}, x_ {2}, x_ {3}, x_ {4}}

x_{1},x_{2},x_{3},x_{4}

top: кольцевой циклид с

x 1 = 3, x 2 = 1, x 3 = - 3, x 4 = - 7 {\ displaystyle x_ {1} = 3, x_ {2} = 1, x_ {3} = - 3, x_ {4} = - 7}

x_{1}=3,x_{2}=1,x_{3}=-3,x_{4}=-7

. в середине: циклид рога с

x 1 = 1, x 2 = 3, x 3 = - 3, x 4 = - 7 {\ displaystyle x_ {1} = 1, x_ {2} = 3, x_ {3} = - 3, x_ {4} = - 7 }

x_{1}=1,x_{2}=3,x_{3}=-3,x_{4}=-7

. внизу: циклид шпинделя с

x 1 = 3, x 2 = - 3, x 3 = 1, x 4 = - 7 {\ displaystyle x_ {1} = 3, x_ {2} = - 3, x_ {3} = 1, x_ {4} = - 7}

x_{1}=3,x_{2}=-3,x_{3}=1,x_{4}=-7

Свойство Максвелла дает основание для определения кольцевого циклида, предписывая его пересечения с осью x:

Дано: четыре точки $x 1>x 2>x 3>x 4 {\ displaystyle x_ {1}>x_ {2}>x_ {3}>x_ {4}}$ $x_{1}>x_ {2}>x_ { 3}>x_ {4}$ on ось x (см. диаграмму).

Требуется: центр $m 0 {\ displaystyle m_ {0}}$ $m_{0}$ , полуоси $a, b {\ displaystyle a, b}$ $a,b$ , линейный эксцентриситет $c {\ displaystyle c}$ $c$ и фокусы эллипса директрисы и параметр $d {\ displaystyle d}$ $d$ соответствующего кольцевого циклида.

Из свойства Максвелла следует

2 (a + d) = x 1 - x 4, 2 (a - d) = x 2 - x 3. {\ displaystyle 2 (a + d) = x_ {1} -x_ {4} \;, \ quad \ 2 (ad) = x_ {2} -x_ {3} \.}

2(a+d)=x_{1}-x_{4}\;,\quad \ 2(a-d)=x_{2}-x_{3}\.

Решение для $a, c {\ displaystyle a, c}$ $a,c$ дает

a = 1 4 (x 1 + x 2 - x 3 - x 4), {\ displaystyle a = {\ frac {1} { 4}} \ left (x_ {1} + x_ {2} -x_ {3} -x_ {4} \ right), \ quad}

a={\frac {1}{4}}\left( x_{1}+x_{2}-x_{3}-x_{4}\right),\quad

d = 1 4 (x 1 - x 2 + x 3 - x 4). {\ displaystyle d = {\ frac {1} {4}} \ left (x_ {1} -x_ {2} + x_ {3} -x_ {4} \ right) \.}

d={\frac {1}{4}}\left(x_{1}-x_{2}+x_{3}-x_{4}\right)\.

Фокус (на ось x) равны

f 1 = 1 2 (x 2 + x 3), f 2 = 1 2 (x 1 + x 4) {\ displaystyle f_ {1} = {\ frac {1} {2 }} (x_ {2} + x_ {3}), \ quad f_ {2} = {\ frac {1} {2}} (x_ {1} + x_ {4})}

f_{1}={\frac {1}{2}}(x_{2}+x_{3}),\quad f_{2}={\frac {1}{2}}(x_{1}+x_{4})

и следовательно,

c = 1 4 (- x 1 + x 2 + x 3 - x 4), b = a 2 - c 2 {\ displaystyle c = {\ frac {1} {4}} \ left (-x_ {1} + x_ {2} + x_ {3} -x_ {4} \ right) \;, \ quad \ b = {\ sqrt {a ^ {2} -c ^ {2}}} \}

c={\frac {1}{4}}\left(-x_{1}+x_{2}+x_{3}-x_{4}\right)\;,\quad \ b={\sqrt {a^{2}-c^{2}}}\

Центр фокальных коник (эллипса и гиперболы) имеет координату x

m 0 = 1 4 (x 1 + x 2 + x 3 + x 4). {\ displaystyle m_ {0} = {\ frac {1} {4}} \ left (x_ {1} + x_ {2} + x_ {3} + x_ {4} \ right) \.}

m_{0}={\frac {1}{4}}\left(x_{1}+x_{2}+x_{3}+x_{4}\right)\.

Если если нужно отобразить циклид с помощью параметрического представления, приведенного выше, необходимо учитывать смещение $m 0 {\ displaystyle m_ {0}}$ $m_{0}$ центра!

Значение порядка чисел $x 1, x 2, x 3, x 4 {\ displaystyle x_ {1}, x_ {2}, x_ {3}, x_ {4}}$ $x_{1},x_{2},x_{3},x_{4}$

(Приведенный выше расчет предполагает $x 1>x 2>x 3>x 4 {\ displaystyle x_ {1}>x_ {2}>x_ {3}>x_ {4}}$ $x_{1}>x_ { 2}>x_ {3}>x_ {4}$ , см. Диаграмму.)

(H) Обмен местами $x 1, x 2 {\ displaystyle x_ {1}, x_ {2}}$ $x_1,x_2$ генерирует рог циклида.. (S) Обмен местами $x 2, x 3 {\ displaystyle x_ {2}, x_ {3}}$ $x_{2},x_{3}$ , генерирует спиндельный циклид.. (H1) Для $x 1 = x 2 = 2 {\ displaystyle x_ {1} = x_ {2} = 2}$ $x_{1}=x_{2}=2$ получается циклид с одним рогом.. (R) Для $x 2 = x 3 = 0 {\ displaystyle x_ {2} = x_ {3} = 0}$ $x_{2}=x_{3}=0$ получается кольцевой циклид, касающийся самого себя в начале координат.

Параллельные поверхности

Параллельные поверхности кольцевого циклида с параметрами

a = 1, b = 0.98, d = 0.30, 0.45, 0.60 {\ displaystyle a = 1, b = 0,98, \ d = 0,30,0,45,0.60}

a=1,b=0.98,\ d=0.30,0.45,0.60

Увеличивая или уменьшая параметр $d {\ displaystyle d}$ $d$ , так что тип не меняется, получается параллельные поверхности (аналогичные параллельным кривым ) одного типа (см. диаграмму).

Гипербола как направляющая

Второй способ создания кольцевого циклида как поверхности канала использует фокальную гиперболу как направляющую. Он имеет уравнение

Циклид с двумя касающимися сферами с центрами на направляющей гиперболе

x 2 c 2 - z 2 b 2 = 1, y = 0. {\ displaystyle {\ frac {x ^ {2}} {c ^ {2}}} - {\ frac {z ^ {2}} {b ^ {2}}} = 1 \, \ y = 0 \. }

{\frac {x^{2}}{c^{2}}}-{\frac {z^{2}}{b^{2}}}=1\,\ y=0\.

В этом случае сферы касаются циклида снаружи во втором семействе окружностей (линиях кривизны). Каждому плечу гиперболы принадлежит подсемейство окружностей. Сферы одного семейства окружают циклид (на диаграмме: фиолетовый). Циклид (синий) касается сфер другого семейства извне.

Параметрическое представление гиперболы:

(± c ch ⁡ ψ, 0, b sinh ⁡ ψ). {\ displaystyle (\ pm c \ cosh \ psi, 0, b \ sinh \ psi) \.}

(\pm c\cosh \psi,0,b\sinh \psi)\.

Радиусы соответствующих сфер равны

R (ψ) = a cosh ⁡ ψ ∓ d. {\ displaystyle R (\ psi) = a \ cosh \ psi \ mp d \.}

R(\psi)=a\cosh \psi \mp d\.

В случае тора ( $c = 0 {\ displaystyle c = 0}$ $c=0$ ) гипербола вырождается в ось тора.

Свойство Максвелла для случая гиперболы. Плечо гиперболы

H + {\ displaystyle H _ {+}}

H_{+}

- это эквидистантная кривая обоих серых кругов.

Свойство Максвелла (случай гиперболы)

Фокусы гиперболы $H ± (ψ) = (± c cosh ⁡ ψ, 0, b sinh ⁡ ψ) {\ displaystyle \; H _ {\ pm} (\ psi) = (\ pm c \ cosh \ psi, 0, b \ sh \ psi) \;}$ $\;H_{\pm }(\psi)=(\pm c\cosh \psi,0,b\sinh \psi)\;$ являются $F i = (± a, 0, 0) {\ displaystyle \; F_ {i} = (\ pm a, 0,0) \;}$ $\;F_{i}=(\pm a,0,0)\;$ . Расстояние до точки гиперболы $H + (ψ) = (c cosh ⁡ ψ, 0, b sinh ⁡ ψ) {\ displaystyle \; H _ {+} (\ psi) = (c \ cosh \ psi, 0, b \ sinh \ psi) \;}$ $\;H_{+}(\psi)=(c\cosh \psi,0,b\sinh \psi)\;$ в фокус $F 1 {\ displaystyle F_ {1}}$ $F_{1}$ is $| H + F 1 | = a cosh ⁡ ψ - c {\ displaystyle \; | H _ {+} F_ {1} | = a \ cosh \ psi -c \;}$ $\;|H_{+}F_{1}|=a\cosh \psi -c\;$ и вместе с радиусом сферы $R + (ψ) = a cosh ⁡ ψ - d {\ displaystyle R _ {+} (\ psi) = a \ cosh \ psi -d}$ $R_{+}(\psi)=a\cosh \psi -d$ получается $| H + F 1 | - R + = d - c {\ displaystyle \; | H _ {+} F_ {1} | -R _ {+} = d-c \;}$ $\;|H_{+}F_{1}|-R_{+}=d-c\;$ . Аналогично получается $| H + F 2 | - R + знак равно d + с {\ displaystyle \; | H _ {+} F_ {2} | -R _ {+} = d + c \;}$ $\;|H_{+}F_{2}|-R_{+}=d+c\;$ . Для точки на втором плече гиперболы выводятся уравнения: $R - - | H - F 1 | = d - c, R - - | H - F 2 | = d + c. {\ displaystyle \; R _ {-} - | H _ {-} F_ {1} | = dc \;, \ R _ {-} - | H _ {-} F_ {2} | = d + c \ ;.}$ $\;R_{-}-|H_{-}F_{1}|=d-c\;,\ R_{-}-|H_{-}F_{2}|=d+c\;.$

Отсюда:

В плоскости xz окружности сфер с центрами $H ± (ψ) {\ displaystyle H _ {\ pm} (\ psi)}$ $H_{\pm }(\psi)$ и радиусы $R ± (ψ) {\ displaystyle R _ {\ pm} (\ psi)}$ $R_{\pm }(\psi)$ имеют две окружности (на серой диаграмме) с центрами $F 1/2 = (± a, 0, 0) {\ displaystyle F_ {1/2} = (\ pm a, 0,0)}$ $F_{1/2}=(\pm a,0,0)$ и радиусы $d ∓ c {\ displaystyle d \ mp c}$ $d\mp c$ как конверты.

Построение точки

Вывод параметрического представления

Эллиптический циклид

Эллипс и гипербола (фокальные коники) - это вырожденные фокальные поверхности эллиптического циклида. Для любой пары $E, H {\ displaystyle E, H}$ $E,H$ точек эллипса и гиперболы верно следующее (из-за определения фокальной поверхности):

1) строка

EH ¯ {\ displaystyle {\ overline {EH}}}

{\overline {EH}}

нормаль к циклиду и

2) соответствующая точка

P {\ displaystyle P}

P

циклида делит хорду

EH {\ displaystyle EH}

EH

с отношением

r: R {\ displaystyle r: R}

r:R

(см. диаграмму).

Из параметрического представления фокальных коник и радиусов сфер

Эллипс:

E (u) = (a cos ⁡ u, b sin ⁡ u, 0), r (u) знак равно d - с соз ⁡ U, {\ Displaystyle \ четырехъядерных \ \ \ E (и) = (а \ соз и, Ь \ грех и, 0), \ четырехъядерных г (и) = постоянного тока \ соз и \ \, }

\quad \ \ \ E(u)=(a\cos u,b\sin u,0),\quad r(u)=d-c\cos u\ \,

Гипербола:

H (v) = (c cos ⁡ v, 0, b tan ⁡ v), R (u) = a cos ⁡ v - d. {\ displaystyle \ quad H (v) = ({\ frac {c} {\ cos v}}, 0, b \ tan v), \ quad R (u) = {\ frac {a} {\ cos v} } -d \.}

\quad H(v)=({\frac {c}{\cos v}},0,b\tan v),\quad R(u)={\frac {a}{\cos v}}-d\.

получает соответствующую точку $P {\ displaystyle P}$ $P$ циклида (см. диаграмму):

P (u, v) = R (v) r (u) + R (v) E (u) + r (u) r (u) + R (v) H (v). {\ Displaystyle \ P (U, v) = {\ гидроразрыва {R (v)} {r (u) + R (v)}} \; E (u) + {\ frac {r (u)} {r (u) + R (v)}} \; H (v) \.}

{\display style \ P(u,v)={\frac {R(v)}{r(u)+R(v)}}\;E(u)+{\frac {r(u)}{r(u)+R(v)}}\;H(v)\.}

(Необычное, но удобное параметрическое представление гиперболы: см. гипербола.)

Детальный расчет приводит к параметрическому представлению эллиптического циклида, заданному выше.

. Если использовать параметрическое представление, данное в статье на поверхностях каналов, то, как правило, только одно семейство параметрических кривых состоит из кругов.

Параболический циклид

Создание параболического циклида в виде поверхности канала

Получение параметрического представления для параболического случая выполняется аналогичным образом:

С параметрическими представлениями фокальных парабол ( вырожденные фокальные поверхности) и радиусы сфер:

P 1 (u) = (p 2 (1 - u 2), pu, 0), r 1 = p 2 (1 - k + u 2) {\ displaystyle P_ {1} (u) = \ left ({\ frac {p} {2}} (1-u ^ {2}), pu, 0 \ right), \ quad r_ {1} = {\ frac { p} {2}} (1-k + u ^ {2}) \;}

P_{1}(u) =\left({\frac {p}{2}}(1-u^{2}),pu,0\right),\quad r_{1}={\frac {p}{2}}(1-k+u^{2})\;

P 2 (v) = (p 2 v 2, 0, pv), r 2 = p 2 (k + v 2) {\ Displaystyle P_ {2} (v) = \ left ({\ frac {p} {2}} v ^ {2}, 0, pv \ right), \ qquad \ qquad r_ {2} = {\ frac {p} {2}} (k + v ^ {2}) \}

P_{2}(v)=\left({\frac {p}{2}}v^{2},0,pv\right),\qquad \qquad r_{2}={\frac {p}{2}}(k+v^{2})\

получается

P (u, v) = r 2 (v) r 1 (u) + r 2 (v) P 1 (и) + р 1 (и) р 1 (и) + р 2 (v) п 2 (v) {\ displaystyle \ P (u, v) = {\ гидроразрыва {r_ {2} (v)} { r_ {1} (u) + r_ {2} (v)}} \; P_ {1} (u) + {\ frac {r_ {1} (u)} {r_ {1} (u) + r_ { 2} (v)}} \; P_ {2} (v)}

\ P(u,v)={\frac {r_{2}(v)}{r_{1}(u)+r_{2}(v)}}\;P_{1}(u)+{\frac {r_{1}(u)}{r_{1}(u)+r_{2}(v)}}\;P_{2}(v)

, который обеспечивает параметрическое представление параболического циклида, приведенное выше.

Циклиды Дюпена и геометрические инверсии

Преимуществом для исследований циклидов является свойство:

(I): Любой циклид Дюпена является изображением любого из правых круговой цилиндр или правый круговой двойной конус или тор вращения посредством инверсии (отражение в сфере).

Инверсия при сфера с уравнением $x 2 + y 2 + z 2 = R 2 {\ displaystyle x ^ {2} + y ^ {2} + z ^ {2} = R ^ {2}}$ $x^2+y^2+z^2=R^2$ можно описать аналитически следующим образом:

(x, y, z) → R 2 ⋅ (x, y, z) x 2 + y 2 + z 2. {\ displaystyle (x, y, z) \ rightarrow {\ frac {R ^ {2} \ cdot (x, y, z)} {x ^ {2} + y ^ {2} + z ^ {2}} } \.}

(x,y,z) \rightarrow \frac{R^2\cdot(x,y,z)}{x^2+y^2+z^2} \.

Наиболее важные свойства инверсии на сфере:

Сферы и круги отображаются на одних и тех же объектах.
Плоскости и линии, содержащие начало координат (центр инверсии), являются отображаются сами на себя.
Плоскости и линии, не содержащие начало координат, отображаются на сферы или окружности, проходящие через начало координат.
Инверсия инволютивно (идентично обратному отображению).
Инверсия сохраняет углы.

С помощью инверсии можно отобразить произвольные поверхности. Приведенные выше формулы в любом случае дают параметрические или неявные представления поверхности изображения, если поверхности заданы параметрически или неявно. В случае параметрической поверхности получаем:

(x (u, v), y (u, v), z (u, v)) → R 2 ⋅ (x (u, v), y (u, v), z (u, v)) x (u, v) 2 + y (u, v) 2 + z (u, v) 2. {\ Displaystyle (Икс (U, v), Y (U, v), Z (U, v)) \ rightarrow {\ frac {R ^ {2} \ cdot (x (u, v), y (u, v), z (u, v))} {x (u, v) ^ {2} + y (u, v) ^ {2} + z (u, v) ^ {2}}} \.}

(x(u,v),y(u,v),z(u,v)) \rightarrow \frac{R^2\cdot(x(u,v),y(u,v),z(u,v))}{x(u,v)^2+y(u,v)^2+z(u,v)^2} \.

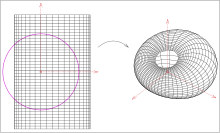
кольцевой циклид, генерируемый инверсией цилиндра в сфере (пурпурный)

параболический кольцевой циклид, генерируемый инверсией цилиндра, содержащего исходный

рог циклид, образованный инверсией конуса

кольцевого циклида порождается инверсией тора

Но: Только в случае правильных круговых цилиндров и конусов и торов вращения получаются циклиды Дюпена и наоборот.

Пример цилиндра

a) Поскольку линии, которые не содержат начало координат, отображаются путем инверсии в сфере (на рисунке: пурпурный) на окружности, содержащие начало координат, изображение цилиндра представляет собой кольцевой циклид с соприкасающимися кругами в начале координат. Как изображения сегментов линии, показанные на рисунке, так и появляются сегменты круга в виде изображений. Сферы, которые касаются цилиндра с внутренней стороны, отображаются на первом пучке сфер, которые образуют циклид как поверхность канала. Изображения касательных плоскостей цилиндра становятся вторым пучком сфер, касающимся циклида. Последние проходят через начало координат.. b) Второй пример инвертирует цилиндр, содержащий начало координат. Линии, проходящие через начало координат, отображаются сами на себя. Следовательно, поверхность неограничена и представляет собой параболический циклид.

Пример конуса

Линии, образующие конус, отображаются на окружности, которые пересекаются в начале координат и изображении вершины конуса. Изображение конуса - двухрогий циклид. На картинке показаны изображения отрезков прямой (конуса), которые на самом деле являются отрезками окружностей.

Пример тора

Оба пучка окружностей на торе (показанном на рисунке) отображаются на соответствующие пучки окружностей на циклиде. В случае самопересекающегося тора получился бы циклид веретена.

Круги Вильярсо

Кольцевой циклид с кругами Вильярсо

Поскольку кольцевые циклиды Дюпена можно рассматривать как изображения торов с помощью подходящих инверсий, а инверсия отображает круг на круг или линию, изображения Окружности Вильярсо образуют еще два семейства окружностей на циклиде (см. Диаграмму).

Определение проектных параметров $a, b, c, d {\ displaystyle a, b, c, d}$ $a,b,c,d$

Формула инверсии параметрической поверхности (см. Выше) обеспечивает параметрическое представление циклида (как инверсия тора) с окружностями как параметрическими кривыми. Но точки параметрической сети плохо распределены. Поэтому лучше рассчитать проектные параметры $a, b, c, d {\ displaystyle a, b, c, d}$ $a,b,c,d$ и использовать параметрическое представление выше:

Cyclide (синий) как изображение путем инверсии тора (черный) на единичной сфере (красный)

Дано: Тор, который смещен из стандартного положения вдоль оси x. Пусть будет $x 1, x 2, x 3, x 4 {\ displaystyle x_ {1}, x_ {2}, x_ {3}, x_ {4}}$ $x_{1},x_{2},x_{3},x_{4}$ пересечения тора с осью абсцисс (см. диаграмму). Все не ноль. В противном случае инверсия тора не была бы кольцевым циклидом.. Требуются: полуоси $a, b {\ displaystyle a, b}$ $a,b$ и линейный эксцентриситет $c {\ displaystyle c}$ $c$ эллипса (директрисы) и параметр $d {\ displaystyle d}$ $d$ кольца-циклида, который представляет собой изображение тора при инверсии на юнитсфера.

Инверсия отображает $xi {\ displaystyle x_ {i}}$ $x_{i}$ на $1 xi {\ displaystyle {\ tfrac {1} {x_ {i}}}}$ ${\tfrac {1}{x_{i}}}$ , которые представляют собой x-координаты 4 точек кольца-циклида (см. Диаграмму). Из раздела Циклид через 4 точки на оси x получается

a = 1 4 (1 x 1 + 1 x 2 - 1 x 3 - 1 x 4), {\ displaystyle a = { \ frac {1} {4}} \ left ({\ frac {1} {x_ {1}}} + {\ frac {1} {x_ {2}}} - {\ frac {1} {x_ {3 }}} - {\ frac {1} {x_ {4}}} \ right), \ quad}

a={\frac {1}{4}}\left({\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}-{\frac {1}{x_{3}}}-{\frac {1}{x_{4}}}\right),\quad

d = 1 4 (- 1 x 1 + 1 x 2 - 1 x 3 + 1 x 4) { \ displaystyle d = {\ frac {1} {4}} \ left (- {\ frac {1} {x_ {1}}} + {\ frac {1} {x_ {2}}} - {\ frac { 1} {x_ {3}}} + {\ frac {1} {x_ {4}}} \ right) \}

d={\frac {1}{4}}\left(-{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}-{\frac {1}{x_{3}}}+{\frac {1}{x_{4}}}\right)\

c = 1 4 (1 x 1 - 1 x 2 - 1 x 3 + 1 x 4), b = a 2 - c 2 {\ displaystyle c = {\ frac {1} {4}} \ left ({\ frac {1} {x_ {1}}} - { \ frac {1} {x_ {2}}} - {\ frac {1} {x_ {3}}} + {\ frac {1} {x_ {4}}} \ right) \;, \ quad \ b = {\ sqrt {a ^ {2} -c ^ {2}}} \}

c={\frac {1}{4}}\left({\frac {1}{x_{1}}}-{\frac {1}{x_{2}}}-{\frac {1}{x_{3}}}+{\frac {1}{x_{4}}}\right)\;,\quad \ b={\sqrt {a^{2}-c^{2}}}\

Центр фокусных коник имеет координату x

m 0 = 1 4 (1 x 1 + 1 x 2 + 1 х 3 + 1 х 4). {\ displaystyle m_ {0} = {\ frac {1} {4}} \ left ({\ frac {1} {x_ {1}}} + {\ frac {1} {x_ {2}}} + { \ frac {1} {x_ {3}}} + {\ frac {1} {x_ {4}}} \ right) \.}

m_{0}={\frac {1}{4}}\left({\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+{\frac {1}{x_{3}}}+{\frac {1}{x_{4}}}\right)\.

Разделение переменных

Циклиды Дюпена - особый случай более общего понятия циклиды, которое является естественным расширением понятия квадратичной поверхности. В то время как квадрика может быть описана как набор нулей полинома второго порядка в декартовых координатах (x 1,x2,x3), циклид задается набором нулей полинома второго порядка в (x 1,x2,x3, r), где г = х 1+x2+x3. Таким образом, это поверхность четвертой степени в декартовых координатах с уравнением вида:

A r 4 + ∑ i = 1 3 P ixir 2 + ∑ i, j = 1 3 Q ijxixj + ∑ i = 1 3 R ixi + В = 0 {\ displaystyle Ar ^ {4} + \ sum _ {i = 1} ^ {3} P_ {i} x_ {i} r ^ {2} + \ sum _ {i, j = 1} ^ {3} Q_ {ij} x_ {i} x_ {j} + \ sum _ {i = 1} ^ {3} R_ {i} x_ {i} + B = 0}

Ar^{4}+\sum _{{i=1}}^{3}P_{i}x_{i}r^{2}+\sum _{{i,j=1}}^{3}Q_{{ij}}x_{i}x_{j}+\sum _{{i=1}}^{3}R_{i}x_{i}+B=0

где Q - матрица 3x3, P и R - трехмерные векторы, а A и B - константы.

Семейства циклидов порождают различные геометрии циклических координат.

В диссертации Максима Бохера 1891 года Ueber die Reihenentwickelungen der Potentialtheorie было показано, что уравнение Лапласа в трех переменных может быть решено с использованием разделения переменных в 17 конформно различных геометриях квадратичных и циклических координат. Многие другие циклические геометрии могут быть получены путем изучения R-разделения переменных для уравнения Лапласа.

См. Также

Инверсия кривых и поверхностей (немецкий)

Примечания

Ссылки

Сесил, Томас Э. (1992), Геометрия сферы Ли, Нью-Йорк: Universitext, Springer-Verlag, ISBN 978-0-387-97747-8.
Эйзенхарт, Лютер П.. (1960), «§133 Циклиды Дюпена», Трактат о дифференциальной геометрии кривых и поверхностей, Нью-Йорк: Довер, стр. 312–314.
Гильберт, Дэвид ; Кон-Фоссен, Стефан (1999), Геометрия и воображение, Американское математическое общество, ISBN 0-8218-1998-4.
Мун, Парри; Спенсер, Домина Эберле (1961), Справочник по теории поля: включая системы координат, дифференциальные уравнения и их решения, Springer, ISBN 0-387-02732-7.
О'Коннор, Джон J.; Робертсон, Эдмунд Ф. (2000), «Пьер Шарль Франсуа Дюпен», Архив истории математики MacTutor.
Пинкалл, Ульрих (1986), «§3.3 Циклиды Дюпена», в G Фишер (редактор), Математические модели из собраний университетов и музеев, Брауншвейг, Германия: Vieweg, стр. 28–30.
Миллер, Уиллард (1977), Симметрия и разделение переменных.
А. Кэли (1873 г.) "На циклиде", Ежеквартальный журнал чистой и прикладной математики 12: стр. 148–163.
В. Чандру, Д. Дутта, К.М. Хоффманн (1989) "О геометрии циклид Дюпена", Визуальный компьютер. (5), стр. 277–290.
С. Дюпен (1822) Приложения де геометрии и механики. Башелье, Париж.
Ф. Кляйн, В. Блашке (1926) Vorlesungen Über Höhere Geometrie. Springer-Verlag, ISBN 978-3-642-98494-5, p. 56.
J. C. Maxwell (1868) "On the cyclide", Quarterly Journal of Pure and Applied Mathematics 9: p. 111–126.
M. J. Pratt (1989) Cyclide Blending in Solid Modelling. In: Wolfgang Strasser, Hans-Peter Seidel (Hrsg.): Theory and Practice in Geometric Modelling. Springer-Verlag, ISBN 0-387-51472-4, p. 235.
Y. L. Srinivas, V. Kumar, D. Dutta (1996) "Surface design using cyclide patches", Computer-Aided Design 28(4): 263–276.
Mabel M. Young (1916) "Dupin's cyclide as a self-dual surface", American Journal of Mathematics 38(3): 269–286

External links

Wikimedia Commons has media related to Dupin cyclide.

Weisstein, Eric W. "Cyclide". MathWorld.
E. Berberich, M. Kerber: Arrangements on Surfaces of Genus One: Tori and Dupin Cyclides.