Аналитический сигнал

В математике и обработке сигналов, аналитический сигнал - это комплексная функция, не имеющая компонентов отрицательной частоты. Реальная и мнимая части аналитического сигнала - это функции с действительными значениями, связанные друг с другом с помощью преобразования Гильберта.

Аналитическое представление функции вещественных значений имеет следующий вид: аналитический сигнал, содержащий исходную функцию и ее преобразование Гильберта. Это представление облегчает многие математические манипуляции. Основная идея заключается в том, что отрицательные частотные компоненты преобразования Фурье (или спектра ) действительной функции являются излишними из-за эрмитовой симметрии функции такой спектр. Эти отрицательные частотные составляющие можно отбросить без потери информации, при условии, что вместо этого вы захотите иметь дело с комплексной функцией. Это делает определенные атрибуты функции более доступными и облегчает получение методов модуляции и демодуляции, таких как односторонняя полоса.

Пока управляемая функция не имеет отрицательных частотных составляющих (то есть она все еще аналитическая), преобразование из комплексного обратно в реальное - это просто вопрос отбрасывания мнимой части. Аналитическое представление является обобщением концепции фазора : в то время как вектор ограничен неизменными во времени амплитудой, фазой и частотой, аналитический сигнал допускает параметры, изменяющиеся во времени.

• 1 Определение
  • 1.1 Отрицательные частотные составляющие
• 2 Примеры
  • 2.1 Пример 1
  • 2.2 Пример 2
  • 2.3 Пример 3
• 3 Свойства
  • 3.1 Мгновенная амплитуда и фаза
  • 3.2 Комплексная огибающая / основная полоса
• 4 Расширения аналитического сигнала до сигналов нескольких переменных
  • 4.1 Многомерный аналитический сигнал на основе специального направления
  • 4.2 Моногенный сигнал
• 5 См. Также
  • 5.1 Приложения
• 6 Примечания
• 7 Ссылки
• 8 Дополнительная литература
• 9 Внешние ссылки

Передаточная функция для создания аналитического сигнала

Если $s\; (t)\; \{\backslash \; displaystyle\; s\; (t)\}$- функция с действительным знаком с преобразованием Фурье $S\; (f)\; \{\backslash \; displaystyle\; S\; (f)\}$, тогда преобразование имеет эрмитову симметрию относительно оси $f\; =\; 0\; \{\backslash \; displaystyle\; f\; =\; 0\}$:

$S\; (-\; f)\; =\; S\; (f)\; \ast ,\; \{\; \backslash \; Displaystyle\; S\; (-f)\; =\; S\; (f)\; ^\; \{*\},\}$

где $S\; (f)\; \ast \; \{\backslash \; displaystyle\; S\; (f)\; ^\; \{*\}\}$- это комплексно сопряженное из $S\; (f)\; \{\backslash \; di\; splaystyle\; S\; (f)\}$. Функция:

, где

• $u\; \; (f)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{u\}\; (f)\}$- Ступенчатая функция Хевисайда,
• $sgn\; \; (f)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{sgn\}\; (f)\}$- знаковая функция ,

содержит только неотрицательные частотные компоненты $S\; (е)\; \{\backslash \; Displaystyle\; S\; (f)\}$. И операция обратима из-за эрмитовой симметрии $S\; (f)\; \{\backslash \; displaystyle\; S\; (f)\}$:

. Аналитический сигнал из $s\; (t)\; \{\backslash \; displaystyle\; s\; (t)\}$- это обратное преобразование Фурье для $S\; a\; (f)\; \{\backslash \; displaystyle\; S\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (f)\}$:

$sa\; (t)\; \triangleq \; F\; -\; 1\; [S\; a\; (f)]\; =\; F\; -\; 1\; [S\; (f)\; +\; sign\; \; (f)\; \cdot \; S\; (f)]\; =\; F\; -\; 1\; \{S\; (f)\}\; ⏟\; s\; (t)\; +\; F\; -\; 1\; \{sign\; \; (f)\}\; ⏟\; j\; 1\; \pi \; t\; \ast \; F\; -\; 1\; \{S\; (f)\}\; ⏟\; s\; (t)\; ⏞\; свертка\; =\; s\; (t)\; +\; j\; [1\; \pi \; t\; \ast \; s\; (t)]\; ⏟\; H\; \; [s\; (t)]\; =\; s\; (t)\; +\; js\; ^\; (t),\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)\; \backslash \; треугольникq\; \{\backslash \; mathcal\; \{F\}\}\; ^\; \{-\; 1\}\; [S\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (f)]\; \backslash \backslash \; =\; \{\backslash \; mathcal\; \{F\}\}\; ^\; \{-\; 1\}\; [S\; (f)\; +\; \backslash \; operatorname\; \{sgn\}\; (f)\; \backslash \; cdot\; S\; (\; f)]\; \backslash \backslash \; =\; \backslash \; underbrace\; \{\{\backslash \; mathcal\; \{F\}\}\; ^\; \{-\; 1\}\; \backslash \; \{S\; (f)\; \backslash \}\}\; \_\; \{s\; (t)\}\; +\; \backslash \; overbrace\; \{\backslash \; underbrace\; \{\{\backslash \; mathcal\; \{F\; \}\}\; ^\; \{-\; 1\}\; \backslash \; \{\backslash \; operatorname\; \{sgn\}\; (f)\; \backslash \}\}\; \_\; \{j\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; t\}\}\}\; *\; \backslash \; underbrace\; \{\{\backslash \; mathcal\; \{F\}\}\; ^\; \{-\; 1\}\; \backslash \; \{S\; (f)\; \backslash \}\}\; \_\; \{s\; (t)\}\}\; ^\; \{\backslash \; text\; \{convolution\}\}\; \backslash \backslash \; =\; s\; (t)\; +\; j\; \backslash \; underbrace\; \{\backslash \; left\; [\{1\; \backslash \; over\; \backslash \; pi\; t\; \}\; *\; s\; (t)\; \backslash \; right]\}\; \_\; \{\backslash \; operatorname\; \{\backslash \; mathcal\; \{H\}\}\; [s\; (t)]\}\; \backslash \backslash \; =\; s\; (t)\; +\; j\; \{\backslash \; hat\; \{s\}\}\; (t),\; \backslash \; конец\; \{выровнен\}\}\}$

где

• $s\; ^\; (t)\; \triangleq \; H\; \; [s\; (t)]\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{s\}\}\; (t)\; \backslash \; треугольникq\; \backslash \; operatorname\; \{\backslash \; mathcal\; \{H\}\; \}\; [s\; (t)]\}$- это преобразование Гильберта из $s\; (t)\; \{\backslash \; displaystyle\; s\; (t)\}$;
• $\ast \; \{\backslash \; displaystyle\; *\}$- символ свертки ;
• $j\; \{\backslash \; displaystyle\; j\}$- мнимая единица.

. Отметим, что $s\; (t)\; =\; s\; (t)\; \ast \; \delta \; (t),\; \{\backslash \; displaystyle\; s\; (t)\; =\; s\; (t)\; *\; \backslash \; delta\; (t),\}$это также можно выразить как операцию фильтрации, которая непосредственно удаляет отрицательные частотные составляющие :

$sa\; (t)\; =\; s\; (t)\; \ast \; [\delta \; (t)\; +\; j\; 1\; \pi \; t]\; ⏟\; F\; -\; 1\; \{2\; u\; (f)\}.\; \{\backslash \; Displaystyle\; s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)\; =\; s\; (t)\; *\; \backslash \; underbrace\; \{\backslash \; left\; [\backslash \; delta\; (t)\; +\; j\; \{1\; \backslash \; over\; \backslash \; pi\; t\}\; \backslash \; right]\}\; \_\; \{\{\backslash \; mathcal\; \{F\}\}\; ^\; \{-\; 1\}\; \backslash \; \{2u\; (f)\; \backslash \}\}.\}$

Отрицательные частотные компоненты

Так как $s\; (t)\; =\; Re\; \; [sa\; (t)]\; \{\; \backslash \; displaystyle\; s\; (t)\; =\; \backslash \; operatorname\; \{Re\}\; [s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)]\}$, восстановление отрицательных частотных составляющих - это простой вопрос отбрасывания $Im\; \; [\; sa\; (t)]\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Im\}\; [s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)]\}$, что может показаться нелогичным. Мы также можем отметить, что комплексное сопряжение $s\; a\; \ast \; (t)\; \{\backslash \; displaystyle\; s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; ^\; \{*\}\; (t)\}$содержит только отрицательные частотные компоненты. И поэтому $s\; (t)\; =\; Re\; \; [sa\; \ast \; (t)]\; \{\backslash \; displaystyle\; s\; (t)\; =\; \backslash \; operatorname\; \{Re\}\; [s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; ^\; \{*\}\; (t)]\}$восстанавливает подавленные положительные частотные составляющие. Другая точка зрения состоит в том, что мнимая составляющая в любом случае - это член, который вычитает частотные составляющие из s (t). Оператор $Re\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Re\}\}$удаляет вычитание, создавая впечатление добавления новых компонентов.

Пример 1

$s\; (t)\; =\; cos\; \; (\omega \; t),\; \{\backslash \; displaystyle\; s\; (t)\; =\; \backslash \; cos\; (\backslash \; omega\; t),\}$где $\omega >0.\; \{\backslash \; displaystyle\; \backslash \; omega>0.\}$

Тогда:

$s\; ^\; (t)\; =\; cos\; \; (\omega \; t\; -\; \pi \; 2)\; =\; sin\; \; (\omega \; t),\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{s\}\}\; (\; t)\; =\; \backslash \; cos\; \backslash \; left\; (\backslash \; omega\; t\; -\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (\backslash \; omega\; t),\}$

$sa\; (t)\; =\; s\; (t)\; +\; js\; ^\; (T)\; знак\; равно\; соз\; \; (\omega \; T)\; +\; J\; грех\; \; (\omega \; T)\; =\; Ej\; \omega \; T.\; \{\backslash \; Displaystyle\; s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)\; =\; s\; (t)\; +\; j\; \{\backslash \; hat\; \{s\; \}\}\; (t)\; =\; \backslash \; cos\; (\backslash \; omega\; t)\; +\; j\; \backslash \; sin\; (\backslash \; omega\; t)\; =\; e\; ^\; \{j\; \backslash \; omega\; t\}.\}$Третье равенство - это формула Эйлера.

A следствие из формулы Эйлера : $cos\; \; (\omega \; t)\; =\; 1\; 2\; (ej\; \omega \; t\; +\; ej\; (-\; \omega )\; t).\; \{\backslash \; displaystyle\; \backslash \; cos\; (\backslash \; omega\; t)\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \; left\; (e\; ^\; \{j\; \backslash \; omega\; t\}\; +\; e\; ^\; \{j\; (-\; \backslash \; omega)\; t\}\; \backslash \; right).\}$В общем, аналитический представление простой синусоиды получается выражением ее в терминах комплексных экспонент, отбрасывая отрицательную частотную составляющую и удваивая положительную частотную составляющую энт. А аналитическое представление суммы синусоид - это сумма аналитических представлений отдельных синусоид.

Пример 2

Здесь мы используем формулу Эйлера, чтобы идентифицировать и отбросить отрицательную частоту.

$s\; (t)\; знак\; равно\; соз\; \; (\omega \; t\; +\; \theta )\; =\; 1\; 2\; (ej\; (\omega \; t\; +\; \theta )\; +\; e\; -\; j\; (\omega \; t\; +\; \theta ))\; \{\backslash \; displaystyle\; s\; (t)\; =\; \backslash \; cos\; (\backslash \; омега\; t\; +\; \backslash \; theta)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (e\; ^\; \{j\; (\backslash \; omega\; t\; +\; \backslash \; theta)\}\; +\; e\; ^\; \{-\; j\; (\backslash \; omega\; t\; +\; \backslash \; theta)\}\; \backslash \; right)\}$

Тогда:

Пример 3

Это еще один пример использования метода преобразования Гильберта для удаления отрицательных частотных составляющих. Заметим, что ничто не мешает нам вычислить $sa\; (t)\; \{\backslash \; displaystyle\; s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)\}$для комплексного значения $s\; (t)\; \{\backslash \; displaystyle\; s\; (t)\}$. Но это может быть не обратимое представление, потому что исходный спектр в целом несимметричен. Таким образом, за исключением этого примера, в общем обсуждении предполагается, что вещественное значение $s\; (t)\; \{\backslash \; displaystyle\; s\; (t)\}$.

$s\; (t)\; =\; e\; -\; j\; \omega \; t\; \{\backslash \; displaystyle\; s\; (t)\; =\; e\; ^\; \{-\; j\; \backslash \; omega\; t\}\}$, где $\omega >0\; \{\backslash \; displaystyle\; \backslash \; omega>0\}$.

Затем:

$s\; ^\; (t)\; =\; je\; -\; j\; \omega \; t,\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{s\}\}\; (t)\; =\; je\; ^\; \{-\; j\; \backslash \; omega\; t\},\}$

$sa\; (t)\; =\; e\; -\; j\; \omega \; t\; +\; j\; 2\; e\; -\; j\; \omega \; t\; =\; e\; -\; j\; \omega \; T\; -\; E\; -\; J\; \omega \; T\; =\; 0.\; \{\backslash \; Displaystyle\; s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)\; =\; e\; ^\; \{-\; j\; \backslash \; omega\; t\}\; +\; j\; ^\; \{2\}\; e\; ^\; \{-\; j\; \backslash \; omega\; t\}\; =\; e\; ^\; \{-\; j\; \backslash \; omega\; t\}\; -e\; ^\; \{-\; j\; \backslash \; omega\; t\}\; =\; 0.\}$

Мгновенные амплитуда и фаза

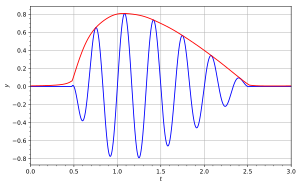
Функция, выделенная синим цветом, и величина ее аналитическое представление красным цветом, показывающее эффект огибающей.

Аналитический сигнал также может быть выражен в полярных координатах :

$sa\; (t)\; =\; sm\; (t)\; ej\; \varphi \; (t),\; \{\backslash \; displaystyle\; s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)\; =\; s\; \_\; \{\backslash \; mathrm\; \{m\}\}\; (t)\; e\; ^\; \{j\; \backslash \; phi\; (t)\},\}$

где вводятся следующие изменяющиеся во времени величины:

• $s\; m\; (t)\; \triangleq \; |\; s\; a\; (t)\; |\; \{\backslash \; displaystyle\; s\; \_\; \{\backslash \; mathrm\; \{m\}\}\; (t)\; \backslash \; triangleq\; |\; s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)\; |\}$называется мгновенной амплитудой или огибающей ;
• $\varphi \; (t)\; \triangleq \; arg\; [са\; (t)]\; \{\backslash \; displaystyle\; \backslash \; phi\; (t)\; \backslash \; треугольникq\; \backslash \; arg\; \backslash !\; \backslash \; left\; [s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)\; \backslash \; right]\}$называется мгновенной фазой или фазовым углом.

На прилагаемой диаграмме синяя кривая изображает $s\; (t)\; \{\backslash \; displaystyle\; s\; (t)\}$и красная кривая изображает соответствующую $см\; (t)\; \{\backslash \; displaystyle\; s\; \_\; \{\backslash \; mathrm\; \{m\}\}\; (t)\}$.

Производная по времени от развернутой мгновенной фазы имеет единицы радиан / секунду, и называется мгновенной угловой частотой:

$\omega \; (t)\; \triangleq \; d\; \varphi \; dt\; (t).\; \{\backslash \; displaystyle\; \backslash \; omega\; (t)\; \backslash \; треугольникq\; \{\backslash \; frac\; \{d\; \backslash \; phi\}\; \{dt\}\}\; (t).\}$

мгновенная частота (в герцах ) следовательно:

$f\; (t)\; \triangleq \; 1\; 2\; \pi \; \omega \; (t).\; \{\backslash \; displaystyle\; f\; (t)\; \backslash \; Triangleq\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; pi\}\}\; \backslash \; omega\; (t).\}$

Мгновенная амплитуда, мгновенная фаза и частота используются в некоторых приложениях для измерения и обнаружения локальные особенности сигнала. Другое применение аналитического представления сигнала относится к демодуляции модулированных сигналов. Полярные координаты удобно разделяют эффекты амплитудной модуляции и фазовой (или частотной) модуляции и эффективно демодулируют определенные виды сигналов.

Комплексная огибающая / основная полоса

Аналитические сигналы часто смещены по частоте (преобразованы с понижением частоты) в сторону 0 Гц, что может создавать [несимметричные] отрицательные частотные компоненты:

$sa\; \downarrow \; (t)\; \triangleq \; sa\; (t)\; е\; -\; j\; \omega \; 0\; T\; знак\; равно\; sm\; (t)\; ej\; (\varphi \; (t)\; -\; \omega \; 0\; t),\; \{\backslash \; displaystyle\; \{s\; \_\; \{\backslash \; mathrm\; \{a\}\}\}\; \_\; \{\backslash \; downarrow\}\; (t)\; \backslash \; треугольник\; q\; s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)\; e\; ^\; \{-\; j\; \backslash \; omega\; \_\; \{0\}\; t\}\; =\; s\; \_\; \{\backslash \; mathrm\; \{m\}\}\; (t)\; e\; ^\; \{j\; (\backslash \; phi\; (t)\; -\; \backslash \; omega\; \_\; \{0\}\; t)\},\}$

где $\omega \; 0\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{0\}\}$- произвольная опорная угловая частота.

Эта функция имеет различные названия, такие как сложный конверт и сложный baseband. Сложный конверт не уникален; он определяется выбором $\omega \; 0\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{0\}\}$. Эта концепция часто используется при работе с сигналами полосы пропускания. Если $s\; (t)\; \{\backslash \; displaystyle\; s\; (t)\}$является модулированным сигналом, $\omega \; 0\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{0\}\}$может быть приравнивается к его несущей частоте.

. В других случаях $\omega \; 0\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{0\}\}$выбирается где-то посередине желаемой полосы пропускания. Тогда простой фильтр нижних частот с действительными коэффициентами может вырезать интересующую часть. Другой мотив - снизить максимальную частоту, что снижает минимальную скорость выборки без псевдонимов. Сдвиг частоты не подрывает математическую управляемость представления комплексного сигнала. Таким образом, в этом смысле сигнал, преобразованный с понижением частоты, остается аналитическим. Однако восстановление представления с действительным знаком - это уже не просто извлечение реального компонента. Может потребоваться преобразование с повышением частоты, и если сигнал был дискретизирован (дискретное время), также может потребоваться интерполяция (повышающая дискретизация ), чтобы избежать алиасинг.

Если $\omega \; 0\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{0\}\}$выбрано больше максимальной частоты $sa\; (t),\; \{\backslash \; displaystyle\; s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t),\}$, затем $sa\; \downarrow \; (t)\; \{\backslash \; displaystyle\; \{s\; \_\; \{\backslash \; mathrm\; \{a\}\}\}\; \_\; \{\backslash \; downarrow\}\; (t)\}$не имеет положительных частот. В этом случае извлечение реального компонента восстанавливает их, но в обратном порядке; низкочастотные компоненты теперь высокие, и наоборот. Это может использоваться для демодуляции типа сигнала одной боковой полосы, называемого нижней боковой полосой или инвертированной боковой полосой.

Другие варианты задания частоты

Иногда $\omega \; 0\; \{\backslash \; displaystyle\; \backslash \; омега\; \_\; \{0\}\}$выбрано, чтобы минимизировать

$\int \; 0\; +\; \infty \; (\omega \; -\; \omega \; 0)\; 2\; |\; S\; a\; (\omega )\; |\; 2\; d\; \omega .\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{+\; \backslash \; infty\}\; (\backslash \; omega\; -\; \backslash \; omega\; \_\; \{0\})\; ^\; \{2\}\; |\; S\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (\backslash \; omega)\; |\; ^\; \{2\}\; \backslash ,\; d\; \backslash \; omega.\}$

В качестве альтернативы можно выбрать $\omega \; 0\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{0\}\}$, чтобы минимизировать среднеквадратичную ошибку при линейной аппроксимации развернутой мгновенной фазы $\varphi \; (t)\; \{\backslash \; displaystyle\; \backslash \; phi\; (t)\}$:

$\int \; -\; \infty \; +\; \infty \; [\omega \; (t)\; -\; \omega \; 0]\; 2\; |\; s\; a\; (t)\; |\; 2\; dt\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{+\; \backslash \; infty\}\; [\backslash \; omega\; (t)\; -\; \backslash \; omega\; \_\; \{0\}]\; ^\; \{2\}\; |\; s\; \_\; \{\backslash \; mathrm\; \{a\}\}\; (t)\; |\; ^\; \{2\}\; \backslash ,\; dt\}$

или другая альтернатива (для некоторого оптимального $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$):

$\int \; -\; \infty \; +\; \infty \; [\varphi \; (t)\; -\; (\omega \; 0\; t\; +\; \theta )]\; 2\; dt.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{+\; \backslash \; infty\}\; [\backslash \; phi\; (t)\; -\; (\backslash \; omega\; \_\; \{0\}\; t\; +\; \backslash \; theta)]\; ^\; \{2\}\; \backslash ,\; dt.\}$

В В области частотно-временной обработки сигналов было показано, что аналитический сигнал был необходим для определения распределения Вигнера – Вилля, чтобы метод мог иметь желаемые свойства, необходимые для практических приложений.

Иногда фраза «комплексная огибающая» имеет более простой смысл комплексной амплитуды вектора (постоянной частоты); в других случаях комплексная огибающая $s\; m\; (t)\; \{\backslash \; displaystyle\; s\_\; \{m\}\; (t)\}$, как определено выше, интерпретируется как зависящее от времени обобщение комплексной амплитуды. Их соотношение мало чем отличается от реального случая: изменяющаяся огибающая обобщающая константа амплитуда.

Концепция аналитического signal четко определен для сигналов одной переменной, которая обычно является временем. Для сигналов двух или более переменных аналитический сигнал может быть определен по-разному, и ниже представлены два подхода.

Многомерный аналитический сигнал на основе специального направления

Прямое обобщение аналитического сигнала может быть выполнено для многомерного сигнала после того, как установлено, что подразумевается под отрицательными частотами для Это дело. Это можно сделать, введя единичный вектор $u\; ^\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{u\}\}\}\}$в область Фурье и пометив любой частотный вектор $\xi \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; xi\}\}\}$как отрицательное, если . Затем получают аналитический сигнал путем удаления всех отрицательных частот и умножения результата на 2 в соответствии с процедурой, описанной для случая сигналов с одной переменной. Однако нет конкретного направления для $u\; ^\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{u\}\}\}\}$, которое следует выбрать, если нет дополнительных ограничений. Следовательно, выбор $u\; ^\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{u\}\}\}\}$является специальным или зависит от приложения.

Моногенный сигнал

Реальная и мнимая части аналитического сигнала соответствуют двум элементам векторно-значного сигнала, как это определено для сигналов с одной переменной. Однако моногенный сигнал может быть расширен до произвольного числа переменных прямым способом, создавая (n + 1) -мерную векторнозначную функцию для случая сигналов с n переменными.

• Практические соображения по вычислению преобразований Гильберта
• Отрицательная частота

Приложения

• Модуляция с одной боковой полосой
• Квадратурный фильтр
• Причинный фильтр

• Леон Коэн, Частотно-временной анализ, Prentice Hall, Upper Saddle River, 1995.
• Frederick W. King, Hilbert Transforms, vol. II, Cambridge University Press, Кембридж, 2009.
• B. Боашаш, Частотно-временной анализ и обработка сигналов: исчерпывающий справочник, Elsevier Science, Oxford, 2003.

• Аналитические сигналы и фильтры преобразования Гильберта