Лемма Спернера

По поводу теоремы из экстремальной теории множеств см . Теорему Спернера.

В математике, лемма Шпернера является комбинаторным аналогом из теоремы Брауэра о неподвижной точке, которая является эквивалентной ей.

Лемма состояние Шпернера, что каждые шпернеровы окраски ( как описано ниже) в триангуляции из п - мерного симплекса содержит ячейку окрашенную с полным набором цветов.

Первоначальный результат такого рода был доказан Эмануэлем Спернером в связи с доказательствами инвариантности области. Раскраски Спернера использовались для эффективного вычисления фиксированных точек и в алгоритмах поиска корня, а также в алгоритмах справедливого деления (вырезания торта). В настоящее время считается трудноразрешимой вычислительной задачей найти неподвижную точку Брауэра или, что эквивалентно, раскраску Спернера, даже на плоскости, в общем случае. Проблема заключается в том PPAD-полной, класс сложности изобретен Пападимитриу.

Согласно Советской математической энциклопедии (под ред. И. М. Виноградова ), родственная теорема 1929 г. ( Кнастера, Борсука и Мазуркевича ) также стала известна как лемма Спернера - этот момент обсуждается в английском переводе (под ред. М. Хазевинкеля). Сейчас она широко известна как лемма Кнастера – Куратовского – Мазуркевича.

• 1 Заявление
  • 1.1 Одномерный случай
  • 1.2 Двумерный случай
  • 1.3 Многомерный случай
• 2 Доказательство
  • 2.1 Комментарий
• 3 Обобщения
  • 3.1 Подмножества этикеток
  • 3.2 Многогранники
  • 3.3 Вариант радуги
  • 3.4 Множественные надписи
  • 3,5 градуса
  • 3.6 Деревья и циклы
  • 3.7 Кубическая лемма Шпернера
• 4 Приложения
• 5 Эквивалентные результаты
• 6 См. Также
• 7 ссылки
• 8 Внешние ссылки

Одномерный случай

Пример одномерного случая

В одном измерении лемму Спернера можно рассматривать как дискретную версию теоремы о промежуточном значении. В этом случае, по сути, говорится, что если дискретная функция принимает только значения 0 и 1, начинается со значения 0 и заканчивается значением 1, то она должна переключать значения нечетное количество раз.

Двумерный случай

Пример двумерного случая

Наиболее часто упоминается двумерный случай. Утверждается следующее:

Для треугольника ABC и триангуляции T треугольника множество S вершин графа T раскрашено в три цвета таким образом, что

1. A, B и C имеют цвета 1, 2 и 3 соответственно.
2. Каждая вершина на ребре ABC должна быть окрашена только в один из двух цветов концов этого ребра. Например, каждая вершина на AC должна иметь цвет 1 или 3.

Тогда существует треугольник из T, вершины которого раскрашены в три разных цвета. Точнее, таких треугольников должно быть нечетное количество.

Многомерный случай

В общем случае лемма относится к n -мерному симплексу

${\ displaystyle {\ mathcal {A}} = A_ {1} A_ {2} \ ldots A_ {n + 1}.}$

Мы рассматриваем триангуляцию T, которая является непересекающимся делением на меньшие n -мерные симплексы. Обозначим красящего функцию как F  :  S  → {1,2,3,..., п, п + 1}, где S снова множество вершин Т. Правила раскраски таковы: ${\ displaystyle {\ mathcal {A}}}$

1. Вершины большого симплекса раскрашены в разные цвета, т. Е. Для.${\ displaystyle f (A_ {i}) = i}$${\ Displaystyle 1 \ Leq я \ Leq п + 1}$
2. Вершины T, расположенные на любой k -мерной подповерхности большого симплекса

${\ displaystyle A_ {i_ {1}} A_ {i_ {2}} \ ldots A_ {i_ {k + 1}}}$

раскрашены только цветами

${\ displaystyle i_ {1}, i_ {2}, \ ldots, i_ {k + 1}.}$

Тогда существует нечетное количество симплексов из T, вершины которых раскрашены во все n + 1 цвета. В частности, должен быть хотя бы один.

Случайная спернеровская раскраска правильной треугольной формы. Каждый тупик представляет собой RGB-треугольник.

Сначала мы обратимся к двумерному случаю. Рассмотрим граф G, построенный из триангуляции T следующим образом:

Вершины G - это элементы T плюс площадь вне треугольника. Две вершины соединяются ребром, если их соответствующие области имеют общую границу, причем одна конечная точка окрашена в 1, а другая - в 2.

Обратите внимание, что на интервале AB есть нечетное количество границ, окрашенных в 1-2 (просто потому, что A окрашен в 1, B окрашен в 2; и когда мы движемся по AB, должно быть нечетное количество изменений цвета, чтобы получить разные цвета в начале и в конце). Следовательно, вершина G, соответствующая внешней области, имеет нечетную степень. Но известно ( лемма о рукопожатии ), что в конечном графе есть четное число вершин нечетной степени. Таким образом, оставшийся граф, исключая внешнюю область, имеет нечетное число вершин с нечетной степенью, соответствующими членам T.

Легко видеть, что единственная возможная степень треугольника из T равна 0, 1 или 2, и что степень 1 соответствует треугольнику, раскрашенному тремя цветами 1, 2 и 3.

Таким образом, мы получили немного более сильный вывод, который говорит, что в триангуляции T существует нечетное количество (и по крайней мере один) полноцветных треугольников.

Многомерный случай доказывается индукцией по размерности симплекса. Мы применяем те же рассуждения, что и в двумерном случае, чтобы заключить, что в n- мерной триангуляции существует нечетное число полноцветных симплексов.

Комментарий

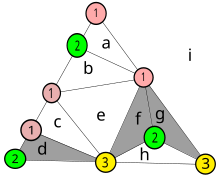Простая двумерная триангуляция примерной фигуры, раскрашенная и названная в соответствии с предположениями леммы Спернера. График, полученный из примера рисунка

Вот уточнение ранее приведенного доказательства для читателя, плохо знакомого с теорией графов.

На этой диаграмме нумеруются цвета вершин приведенного ранее примера. Маленькие треугольники, все вершины которых имеют разные номера, на графике заштрихованы. Каждый маленький треугольник становится узлом в новом графе, полученном в результате триангуляции. Маленькие буквы обозначают области, восемь внутри фигуры, а область i обозначает пространство за ее пределами.

Как описано ранее, те узлы, которые имеют общее ребро, конечные точки которого пронумерованы 1 и 2, соединяются в производном графе. Например, узел d имеет общее ребро с внешней областью i, а все его вершины имеют разные номера, поэтому он также закрашен. Узел b не закрашен, потому что две вершины имеют одинаковые номера, но он присоединен к внешней области.

Можно добавить новый треугольник с полным номером, скажем, вставив узел с номером 3 на ребро между 1 и 1 узла a и соединив этот узел с другой вершиной a. Для этого потребуется создать пару новых узлов, как в случае с узлами f и g.

Подмножества этикеток

Предположим, что каждая вершина триангуляции может быть помечена несколькими цветами, так что функция окраски будет f  :  S  → 2 ^{[n + 1]}.

Для каждого суб-симплекса набор маркировок на его вершинах является набором-семейством над набором цветов. Это семейство множеств можно рассматривать как гиперграф. ${\ Displaystyle [п + 1]}$

Если для каждой вершины на грани симплекса цвета в являются подмножеством набора цветов на концах грани, то существует под-симплекс со сбалансированной разметкой - разметка, в которой соответствующий гиперграф допускает совершенный дробное соответствие. Чтобы проиллюстрировать это, вот несколько примеров сбалансированной маркировки для: ${\ displaystyle v}$${\ Displaystyle f (v)}$ ${\ displaystyle n = 2}$

• ({1}, {2}, {3}) - уравновешиваются весами (1, 1, 1).
• ({1,2}, {2,3}, {3,1}) - уравновешиваются весами (1/2, 1/2, 1/2).
• ({1,2}, {2,3}, {1}) - уравновешивается весами (0, 1, 1).

Это было доказано Шепли в 1973 году. Это комбинаторный аналог леммы KKMS.

Многогранники

Предположим, что вместо -мерного симплекса у нас есть -мерный многогранник с вершинами. ${\ displaystyle n-1}$${\ displaystyle d}$ ${\ displaystyle n}$

Тогда есть по крайней мере полностью помеченные симплексы, где «полностью помечены» означает, что каждая метка на симплексе имеет свой цвет. Например, если (двумерный) многоугольник с n вершинами триангулирован и раскрашен в соответствии с критерием Спернера, то есть по крайней мере полностью помеченные треугольники. ${\ displaystyle nd}$${\ displaystyle n-2}$

Это общее утверждение было выдвинуто Атанасовым в 1996 году, который доказал его на практике. Доказательство общего случая было впервые дано де Лоэрой, Петерсоном и Су в 2002 году. ${\ displaystyle d = 2}$

Вариант радуги

Предположим, что вместо одной разметки у нас есть разные разметки Спернера. ${\ displaystyle n}$

Мы рассматриваем пары (симплекс, перестановка) такие, что метка каждой вершины симплекса выбирается из разных разметок (так что для каждого симплекса существуют разные пары). ${\ displaystyle n!}$

Тогда есть по крайней мере полностью помеченные пары. Это доказал Равиндра Бапат. ${\ displaystyle n!}$

Другой способ сформулировать эту лемму состоит в следующем. Предположим, что есть люди, каждый из которых производит разные разметки Спернера для одной и той же триангуляции. Тогда существует симплекс и соответствие людей его вершинам, так что каждая вершина помечена своим владельцем по-разному (один человек маркирует свою вершину цифрой 1, другой человек маркирует ее вершину цифрой 2 и т. Д.). Более того, таких совпадений не меньше. Это может быть использовано, чтобы найти нарезку для торта без зависти с соединенными кусочками. ${\ displaystyle n}$${\ displaystyle n!}$

Множественные надписи

Предположим, что вместо одной разметки у нас есть разные разметки Спернера. Потом: ${\ displaystyle m}$

1. Для любых положительных целых чисел, сумма которых равна, существует детский симплекс, на котором для каждого числа разметки используются по крайней мере (из) различные метки. Причем каждая метка используется как минимум в одной (вне) маркировке.${\ displaystyle k_ {1}, \ ldots, k_ {m}}$${\ Displaystyle м + п-1}$${\ Displaystyle я \ в \ {1, \ ldots, м \}}$${\ displaystyle i}$${\ displaystyle k_ {i}}$${\ displaystyle n}$${\ displaystyle m}$
2. Для любых положительных целых чисел, сумма которых равна, существует детский симплекс, на котором для каждого метка используется по крайней мере (из) различных разметок.${\ Displaystyle l_ {1}, \ ldots, l_ {n}}$${\ Displaystyle м + п-1}$${\ displaystyle j \ in \ {1, \ ldots, n \}}$${\ displaystyle j}$${\ displaystyle l_ {j}}$${\ displaystyle m}$

Обе версии сводятся к лемме Спернера, когда или когда все разметки идентичны. ${\ displaystyle m = 1}$${\ displaystyle m}$

См. Аналогичные обобщения.

Градусы

Последовательность	Степень
123	1 (один переключатель 1-2 и нет переключателя 2-1)
12321	0 (один переключатель 1-2 минус один переключатель 2-1)
1232	0 (как указано выше; последовательность отзыва циклическая)
1231231	2 (два переключателя 1-2 и нет переключателя 2-1)

Предположим, что треугольник триангулирован и помечен {1,2,3}. Рассмотрим циклическую последовательность меток на границе треугольника. Определите степень маркировки как разницу между количеством переключателей от 1 до 2 и количеством переключателей от 2 до 1. См. Примеры в таблице справа. Обратите внимание, что степень одинакова, если мы считаем переключатели от 2 до 3 минус 3 до 2 или от 3 до 1 минус 1 до 3.

Мусин доказал, что количество полностью помеченных треугольников не меньше степени маркировки. В частности, если степень отлична от нуля, то существует хотя бы один полностью помеченный треугольник.

Если разметка удовлетворяет условию Спернера, то ее степень равна 1: переключатели 1-2 и 2-1 находятся только на стороне между вершинами 1 и 2, а количество переключателей 1-2 должно быть на единицу больше, чем число 2–1 переключений (при переходе от вершины 1 к вершине 2). Следовательно, первоначальная лемма Шпернера следует из теоремы Мусина.

Деревья и циклы

Аналогичная лемма есть о конечных и бесконечных деревьях и циклах.

Кубическая лемма Шпернера

Вариант леммы Спернера о кубе (вместо симплекса) был доказан Гарольдом В. Куном. Это связано с теоремой Пуанкаре – Миранды.

Раскраски Спернера использовались для эффективного вычисления фиксированных точек. Раскраска Спернера может быть построена так, что полностью помеченные симплексы соответствуют неподвижным точкам данной функции. Делая триангуляцию все меньше и меньше, можно показать, что предел полностью помеченных симплексов - это в точности фиксированная точка. Следовательно, этот метод позволяет приблизить фиксированные точки.

По этой причине, лемма Шпернера также может быть использована в алгоритмах корневых ознакомительный и справедливое разделение алгоритмах; см. протоколы Симмонса – Су.

Лемма Спернера - один из ключевых ингредиентов доказательства теоремы Монски о том, что квадрат нельзя разрезать на нечетное количество треугольников равной площади.

Лемму Спернера можно использовать для поиска конкурентного равновесия в экономике обмена, хотя есть более эффективные способы его найти.

Спустя пятьдесят лет после первой публикации Спернер представил обзор развития, влияния и применения своей комбинаторной леммы.

Существует несколько теорем о неподвижной точке, которые представлены в трех эквивалентных вариантах: вариант алгебраической топологии, комбинаторный вариант и вариант покрытия множества. Каждый вариант можно доказать отдельно, используя совершенно разные аргументы, но каждый вариант также можно свести к другим вариантам в своем ряду. Кроме того, каждый результат в верхней строке можно вывести из результата, находящегося под ним в том же столбце.

Алгебраическая топология	Комбинаторика	Установить покрытие
Теорема Брауэра о неподвижной точке	Лемма Спернера	Лемма Кнастера – Куратовского – Мазуркевича.
Теорема Борсука – Улама.	Лемма Такера	Теорема Люстерника – Шнирельмана.

• Топологическая комбинаторика

• Доказательство леммы Шпернера в вырезе на-узле
• Лемма Спернера и игра треугольников на n-богатом сайте.
• Лемма Спернера в 2D, веб-игра на itch.io.