Вытянутые сфероидальные координаты

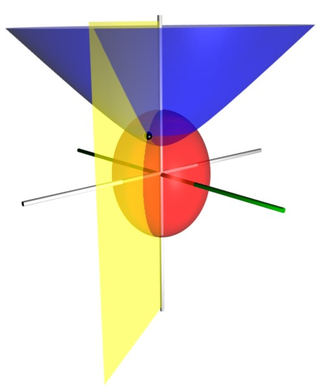
Три координатных поверхности вытянутых сфероидальных координат. Красный вытянутый сфероид (растянутая сфера) соответствует μ = 1, а синий двухлистный гиперболоид соответствует ν = 45 °. Желтая полуплоскость соответствует φ = −60 °, которая измеряется относительно оси x (выделена зеленым). Черная сфера представляет собой точку пересечения трех поверхностей, которая имеет декартовы координаты примерно (0,831, -1,439, 2,182).

Вытянутые сфероидальные координаты являются трехмерными ортогональная система координат, которая возникает в результате вращения двумерной эллиптической системы координат вокруг фокальной оси эллипса, то есть оси симметрии, на которой расположены фокусы. Вращение вокруг другой оси дает сжатые сфероидальные координаты. Вытянутые сфероидальные координаты также можно рассматривать как предельный случай для эллипсоидальных координат, в котором две наименьшие главные оси равны по длине.

Вытянутые сфероидальные координаты могут использоваться для решения различных дифференциальных уравнений в частных производных, в которых граничные условия соответствуют его симметрии и форме, например, решение для поля, создаваемого двумя центрами, которые принимаются как фокусы на оси z. Одним из примеров является решение для волновой функции электрона , движущегося в электромагнитном поле двух положительно заряженных ядер, как в молекулярный ион водорода, H 2. Другой пример - решение для электрического поля, создаваемого двумя небольшими наконечниками электрода. Другие ограничивающие случаи включают области, созданные отрезком линии (μ = 0) или линией с отсутствующим сегментом (ν = 0).

• 1 Определение
• 2 Масштабные коэффициенты
• 3 Альтернативное определение
• 4 Альтернативные масштабные коэффициенты
• 5 Ссылки
• 6 Библиография
  • 6.1 Без условных обозначений углов
  • 6.2 Угол соглашение
  • 6.3 Необычное соглашение
• 7 Внешние ссылки

Выдвинуть сфероидальные координаты μ и ν для a = 1. Линии равных значений μ и ν показаны на плоскости xz, т. е. для φ = 0. Поверхности постоянных μ и ν получаются вращением вокруг оси z, так что диаграмма действительна для любой плоскости, содержащей ось z, т.е. для любого φ.

Наиболее распространенное определение вытянутого сфероидальные координаты $(\mu ,\; \nu ,\; \phi )\; \{\backslash \; displaystyle\; (\backslash \; mu,\; \backslash \; nu,\; \backslash \; varphi)\}$is

$x\; =\; a\; sinh\; \; \mu \; sin\; \; \nu \; cos\; \; \phi \; \{\backslash \; displaystyle\; x\; =\; a\; \backslash \; sinh\; \backslash \; mu\; \backslash \; sin\; \backslash \; nu\; \backslash \; cos\; \backslash \; varphi\}$

$y\; =\; a\; sinh\; \; \mu \; sin\; \; \nu \; sin\; \; \phi \; \{\backslash \; displaystyle\; y\; =\; a\; \backslash \; sinh\; \backslash \; mu\; \backslash \; sin\; \backslash \; nu\; \backslash \; sin\; \backslash \; varphi\; \}$

$z\; =\; a\; cos\; \; \mu \; cos\; \; \nu \; \{\backslash \; displaystyle\; z\; =\; a\; \backslash \; cosh\; \backslash \; mu\; \backslash \; cos\; \backslash \; nu\}$

где $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$- неотрицательный действительное число и $\nu \; \in \; [0,\; \pi ]\; \{\backslash \; displaystyle\; \backslash \; nu\; \backslash \; in\; [0,\; \backslash \; pi]\}$. Азимутальный угол $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$принадлежит интервалу $[0,\; 2\; \pi ]\; \{\backslash \; displaystyle\; [0,2\; \backslash \; pi]\}$.

Тригонометрическое тождество

$z\; 2\; a\; 2\; cosh\; 2\; \; \mu \; +\; x\; 2\; +\; y\; 2\; a\; 2\; sinh\; 2\; \; \mu \; =\; cos\; 2\; \; \nu \; +\; sin\; 2\; \; \nu \; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{z\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\; \backslash \; cosh\; ^\; \{2\}\; \backslash \; mu\}\}\; +\; \{\backslash \; frac\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\; \backslash \; sinh\; ^\; \{2\}\; \backslash \; mu\}\}\; =\; \backslash \; cos\; ^\; \{2\}\; \backslash \; nu\; +\; \backslash \; sin\; ^\; \{2\}\; \backslash \; nu\; =\; 1\}$

показывает, что поверхности постоянной $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$формы вытянуты сфероидов, поскольку они представляют собой эллипсы, повернутые вокруг оси, соединяющей их фокусы. Точно так же гиперболическое тригонометрическое тождество

$z\; 2\; a\; 2\; cos\; 2\; \; \nu \; -\; x\; 2\; +\; y\; 2\; a\; 2\; sin\; 2\; \; \nu \; =\; cosh\; 2\; \; \mu \; -\; sinh\; 2\; \; \mu \; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{z\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\; \backslash \; cos\; ^\; \{2\}\; \backslash \; nu\}\}\; -\; \{\backslash \; frac\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\}\; \backslash \; nu\}\}\; =\; \backslash \; cosh\; ^\; \{2\}\; \backslash \; mu\; -\; \backslash \; sinh\; ^\; \{2\}\; \backslash \; mu\; =\; 1\}$

показывает, что поверхности постоянной $\nu \; \{\backslash \; displaystyle\; \backslash \; nu\}$формы гиперболоиды революции.

Расстояния от фокусов, расположенных в $(x,\; y,\; z)\; =\; (0,\; 0,\; \pm \; a)\; \{\backslash \; displaystyle\; (x,\; y,\; z)\; =\; (0,0,\; \backslash \; pm\; a)\}$равны

$r\; \pm \; =\; x\; 2\; +\; y\; 2\; +\; (z\; \mp \; a)\; 2\; =\; a\; (ch\; \; \mu \; \mp \; cos\; \; \nu ).\; \{\backslash \; displaystyle\; r\; \_\; \{\backslash \; pm\}\; =\; \{\backslash \; sqrt\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; (z\; \backslash \; mp\; a)\; ^\; \{2\}\}\}\; =\; a\; (\backslash \; cosh\; \backslash \; mu\; \backslash \; mp\; \backslash \; cos\; \backslash \; nu).\}$

Масштабные коэффициенты для эллиптических координат $(\mu ,\; \nu )\; \{\backslash \; displaystyle\; (\backslash \; mu,\; \backslash \; nu)\}$равны

$час\; \mu \; знак\; равно\; час\; \nu \; =\; зп\; 2\; \; \mu \; +\; грех\; 2\; \; \nu \; \{\backslash \; displaystyle\; h\; \_\; \{\backslash \; mu\}\; =\; h\; \_\; \{\backslash \; nu\}\; =\; a\; \{\backslash \; sqrt\; \{\backslash \; sinh\; ^\; \{2\}\; \backslash \; mu\; +\; \backslash \; sin\; ^\; \{\; 2\}\; \backslash \; nu\}\}\}$

, тогда как коэффициент азимутального масштаба равен

$h\; \phi \; =\; a\; sinh\; \; \mu \; sin\; \; \nu ,\; \{\backslash \; displaystyle\; h\; \_\; \{\backslash \; varphi\}\; =\; a\; \backslash \; sinh\; \backslash \; mu\; \backslash \; sin\; \backslash \; nu,\}$

, что дает метрику

$ds\; 2\; =\; h\; \mu \; 2\; d\; \mu \; 2\; +\; h\; \nu \; 2\; d\; \nu \; 2\; +\; h\; \phi \; 2\; d\; \phi \; 2\; =\; a\; 2\; [(sinh\; 2\; \; \mu \; +\; sin\; 2\; \; \nu )\; d\; \mu \; 2\; +\; (sh\; 2\; \; \mu \; +\; sin\; 2\; \; \nu )\; d\; \nu \; 2\; +\; (sh\; 2\; \; \mu \; sin\; 2\; \; \nu )\; d\; \phi \; 2].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; ds\; ^\; \{2\}\; =\; h\; \_\; \{\backslash \; mu\}\; ^\; \{2\}\; d\; \backslash \; mu\; ^\; \{2\}\; +\; h\; \_\; \{\backslash \; nu\}\; ^\; \{2\}\; d\; \backslash \; nu\; ^\; \{2\}\; +\; h\; \_\; \{\backslash \; varphi\}\; ^\; \{2\}\; d\; \backslash \; varphi\; ^\; \{2\}\; \backslash \backslash \; =\; a\; ^\; \{2\}\; \backslash \; left\; [(\backslash \; sinh\; ^\; \{2\}\; \backslash \; mu\; +\; \backslash \; sin\; ^\; \{2\}\; \backslash \; nu)\; d\; \backslash \; mu\; ^\; \{2\}\; +\; (\backslash \; sh\; ^\; \{2\}\; \backslash \; mu\; +\; \backslash \; sin\; ^\; \{2\}\; \backslash \; nu)\; d\; \backslash \; nu\; ^\; \{2\}\; +\; (\backslash \; sinh\; ^\; \{2\}\; \backslash \; mu\; \backslash \; sin\; ^\; \{2\}\; \backslash \; nu)\; d\; \backslash \; varphi\; ^\; \{2\}\; \backslash \; right].\; \backslash \; end\; \{align\}\}\}$

Следовательно, бесконечно малый элемент объема равен

$d\; V\; =\; a\; 3\; sinh\; \; \mu \; sin\; \; \nu \; (sinh\; 2\; \; \mu \; +\; sin\; 2\; \; \nu )\; d\; \mu \; d\; \nu \; d\; \phi \; \{\backslash \; displaystyle\; dV\; =\; a\; ^\; \{3\}\; \backslash \; sinh\; \backslash \; mu\; \backslash \; sin\; \backslash \; nu\; (\backslash \; sinh\; ^\; \{2\}\; \backslash \; mu\; +\; \backslash \; sin\; ^\; \{2\}\; \backslash \; nu)\; \backslash ,\; d\; \backslash \; mu\; \backslash ,\; d\; \backslash \; nu\; \backslash ,\; d\; \backslash \; varphi\}$

и лапласиан можно записать как

$\nabla \; 2\; \Phi \; =\; 1\; a\; 2\; (sh\; 2\; \; \mu \; +\; sin\; 2\; \; \nu )\; [\partial \; 2\; \Phi \; \partial \; \mu \; 2\; +\; \partial \; 2\; \Phi \; \partial \; \nu \; 2\; +\; coth\; \; \mu \; \partial \; \Phi \; \partial \; \mu \; +\; детская\; кроватка\; \; \nu \; \partial \; \Phi \; \partial \; \nu ]\; +\; 1\; a\; 2\; sinh\; 2\; \; \mu \; sin\; 2\; \; \nu \; \partial \; 2\; \Phi \; \partial \; \phi \; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; Phi\; =\; \{\}\; \{\backslash \; frac\; \{1\}\; \{a\; ^\; \{2\}\; (\backslash \; sinh\; ^\; \{2\}\; \backslash \; mu\; +\; \backslash \; sin\; ^\; \{2\}\; \backslash \; nu)\}\}\; \backslash \; left\; [\{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; Phi\}\; \{\backslash \; partial\; \backslash \; mu\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; Phi\}\; \{\backslash \; partial\; \backslash \; nu\; ^\; \{2\}\}\}\; +\; \backslash \; coth\; \backslash \; mu\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Phi\}\; \{\backslash \; partial\; \backslash \; mu\}\}\; +\; \backslash \; cot\; \backslash \; nu\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Phi\}\; \{\backslash \; partial\; \backslash \; nu\}\}\; \backslash \; right]\; \backslash \; \backslash \; [6pt]\; \{\}\; +\; \{\backslash \; frac\; \{1\}\; \{a\; ^\; \{2\}\; \backslash \; sinh\; ^\; \{2\}\; \backslash \; mu\; \backslash \; sin\; ^\; \{2\}\; \backslash \; nu\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; Phi\; \}\; \{\backslash \; partial\; \backslash \; varphi\; ^\; \{2\}\}\}\; \backslash \; end\; \{align\}\}\}$

Другие дифференциальные операторы, такие как $\nabla \; \cdot \; F\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{F\}\}$и $\nabla \; \times \; F\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{F\}\}$можно выразить в координатах $(\mu ,\; \nu ,\; \phi )\; \{\backslash \; displaystyle\; (\backslash \; mu,\; \backslash \; nu,\; \backslash \; varphi)\}$путем подстановки масштабных коэффициентов в общие формулы, найденные в ортогональных координатах.

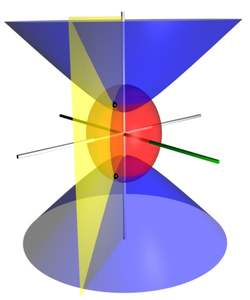
В принципе, определение вытянутых сфероидальных координат может быть вырожденным. Другими словами, один набор координат может соответствовать двум точкам в декартовых координатах ; это проиллюстрировано здесь двумя черными сферами, по одной на каждом листе гиперболоида и расположенными в точках (x, y, ± z). Однако ни одно из представленных здесь определений не является вырожденным.

Альтернативный и геометрически интуитивный набор вытянутых сфероидальных координат $(\sigma ,\; \tau ,\; \varphi )\; \{\backslash \; displaystyle\; (\backslash \; sigma,\; \backslash \; tau,\; \backslash \; phi)\}$иногда используются, где $\sigma \; =\; cosh\; \; \mu \; \{\backslash \; displaystyle\; \backslash \; sigma\; =\; \backslash \; cosh\; \backslash \; mu\}$и $\tau \; =\; cos\; \; \nu \; \{\backslash \; displaystyle\; \backslash \; tau\; =\; \backslash \; cos\; \backslash \; nu\}$. Следовательно, кривые константы $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$представляют собой вытянутые сфероиды, тогда как кривые константы $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$являются гиперболоидами революция. Координата $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$принадлежит интервалу [-1, 1], тогда как координата $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$должна быть больше или равно единице.

Координаты $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$и $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$имеют простое отношение к расстояниям до фокусы $F\; 1\; \{\backslash \; displaystyle\; F\_\; \{1\}\}$и $F\; 2\; \{\backslash \; displaystyle\; F\_\; \{2\}\}$. Для любой точки на плоскости сумма $d\; 1\; +\; d\; 2\; \{\backslash \; displaystyle\; d\_\; \{1\}\; +\; d\_\; \{2\}\}$расстояний до фокусов равна $2\; a\; \sigma \; \{\; \backslash \; displaystyle\; 2a\; \backslash \; sigma\}$, а их разность $d\; 1\; -\; d\; 2\; \{\backslash \; displaystyle\; d\_\; \{1\}\; -d\_\; \{2\}\}$равна $2\; a\; \tau \; \{\backslash \; Displaystyle\; 2а\; \backslash \; тау\}$. Таким образом, расстояние до $F\; 1\; \{\backslash \; displaystyle\; F\_\; \{1\}\}$равно $a\; (\sigma \; +\; \tau )\; \{\backslash \; displaystyle\; a\; (\backslash \; sigma\; +\; \backslash \; tau)\}$, тогда как расстояние до $F\; 2\; \{\backslash \; displaystyle\; F\_\; \{2\}\}$равно $a\; (\sigma \; -\; \tau )\; \{\backslash \; displaystyle\; a\; (\backslash \; sigma\; -\; \backslash \; tau)\}$. (Напомним, что $F\; 1\; \{\backslash \; displaystyle\; F\_\; \{1\}\}$и $F\; 2\; \{\backslash \; displaystyle\; F\_\; \{2\}\}$расположены в $z\; =\; -\; a\; \{\backslash \; displaystyle\; z\; =\; -a\}$и $z\; =\; +\; a\; \{\backslash \; displaystyle\; z\; =\; +\; a\}$соответственно.) Это дает следующие выражения для $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$, $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$и $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$:

$\sigma \; =\; 1\; 2\; a\; (x\; 2\; +\; y\; 2\; +\; (z\; +\; a)\; 2\; +\; x\; 2\; +\; y\; 2\; +\; (z\; -\; a)\; 2)\; \{\backslash \; displaystyle\; \backslash \; sigma\; =\; \{\backslash \; frac\; \{1\}\; \{2a\}\}\; \backslash \; left\; (\{\backslash \; sqrt\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; (z\; +\; a)\; ^\; \{2\}\}\}\; +\; \{\backslash \; sqrt\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; (za)\; ^\; \{2\}\}\}\; \backslash \; right)\}$

$\tau \; знак\; равно\; 1\; 2\; a\; (x\; 2\; +\; y\; 2\; +\; (z\; +\; a)\; 2\; -\; x\; 2\; +\; y\; 2\; +\; (z\; -\; a)\; 2)\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; \{\backslash \; frac\; \{1\}\; \{2a\}\}\; \backslash \; left\; (\{\backslash \; sqrt\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; (z\; +\; a)\; ^\; \{2\}\}\}\; -\; \{\backslash \; sqrt\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; (za)\; ^\; \{\; 2\}\}\}\; \backslash \; right)\}$

$\phi \; =\; arctan\; \; (yx)\; \{\backslash \; displaystyle\; \backslash \; varphi\; =\; \backslash \; arctan\; \backslash \; left\; (\{\backslash \; frac\; \{y\}\; \{x\}\}\; \backslash \; right)\}$

В отличие от аналогичного сжатые сфероидальные координаты, координаты вытянутого сфероида (σ, τ, φ) не вырождены; другими словами, существует уникальное обратимое соответствие между ними и декартовыми координатами

$x\; =\; a\; (\sigma \; 2\; -\; 1)\; (1\; -\; \tau \; 2)\; cos\; \; \phi \; \{\backslash \; displaystyle\; x\; =\; a\; \{\backslash \; sqrt\; \{(\backslash \; sigma\; ^\; \{2\}\; -1)\; (1-\; \backslash \; tau\; ^\; \{2\})\}\}\; \backslash \; cos\; \backslash \; varphi\}$

$y\; =\; a\; (\sigma \; 2\; -\; 1)\; (1\; -\; \tau \; 2)\; грех\; \; \phi \; \{\backslash \; displaystyle\; y\; =\; a\; \{\backslash \; sqrt\; \{(\backslash \; sigma\; ^\; \{2\}\; -1)\; (1-\; \backslash \; tau\; ^\; \{2\})\}\}\; \backslash \; sin\; \backslash \; varphi\}$

$z\; =\; a\; \sigma \; \tau \; \{\backslash \; displaystyle\; z\; =\; a\; \backslash \; \backslash \; sigma\; \backslash \; \backslash \; tau\}$

Масштабные коэффициенты для альтернативных эллиптических координат $(\sigma ,\; \tau ,\; \phi )\; \{\backslash \; displaystyle\; (\backslash \; sigma,\; \backslash \; тау,\; \backslash \; varphi)\}$равны

$час\; \sigma \; =\; a\; \sigma \; 2\; -\; \tau \; 2\; \sigma \; 2\; -\; 1\; \{\backslash \; displaystyle\; h\; \_\; \{\backslash \; sigma\}\; =\; a\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; sigma\; ^\; \{2\}\; -\; \backslash \; tau\; ^\; \{2\}\}\; \{\backslash \; sigma\; ^\; \{2\}\; -1\}\}\}\}$

$час\; \tau \; =\; a\; \sigma \; 2\; -\; \tau \; 2\; 1\; -\; \tau \; 2\; \{\backslash \; displaystyle\; h\; \_\; \{\backslash \; tau\}\; =\; a\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; sigma\; ^\; \{2\}\; -\; \backslash \; tau\; ^\; \{2\}\}\; \{1-\; \backslash \; tau\; ^\; \{2\}\}\}\}$

, а коэффициент азимутального масштаба теперь составляет

$h\; \phi \; =\; a\; (\sigma \; 2-1)\; (1\; -\; \tau \; 2)\; \{\backslash \; displaystyle\; h\; \_\; \{\backslash \; varphi\}\; =\; a\; \{\backslash \; sqrt\; \{\backslash \; left\; (\backslash \; sigma\; ^\; \{2\}\; -1\; \backslash \; right)\; \backslash \; left\; (1-\; \backslash \; tau\; ^\; \{\; 2\}\; \backslash \; right)\}\}\}$

Следовательно, бесконечно малое vo элемент просвета становится

$d\; V\; =\; a\; 3\; (\sigma \; 2\; -\; \tau \; 2)\; d\; \sigma \; d\; \tau \; d\; \phi \; \{\backslash \; displaystyle\; dV\; =\; a\; ^\; \{3\}\; (\backslash \; sigma\; ^\; \{2\}\; -\; \backslash \; tau\; ^\; \{2\})\; \backslash ,\; d\; \backslash \; sigma\; \backslash ,\; d\; \backslash \; tau\; \backslash ,\; d\; \backslash \; varphi\}$

и лапласиан равен

$\nabla \; 2\; \Phi \; =\; 1\; a\; 2\; (\sigma \; 2\; -\; \tau \; 2)\; \{\partial \; \partial \; \sigma \; [(\sigma \; 2\; -\; 1)\; \partial \; \Phi \; \partial \; \sigma ]\; +\; \partial \; \partial \; \tau \; [(1\; -\; \tau \; 2)\; \partial \; \Phi \; \partial \; \tau ]\}\; +\; 1\; a\; 2\; (\sigma \; 2\; -\; 1)\; (1\; -\; \tau \; 2)\; \partial \; 2\; \Phi \; \partial \; \phi \; 2\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; Phi\; =\; \{\}\; \{\backslash \; frac\; \{1\}\; \{a\; ^\; \{2\}\; (\backslash \; sigma\; ^\; \{2\}\; -\; \backslash \; tau\; ^\; \{2\})\}\}\; \backslash \; left\; \backslash \; \{\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; sigma\}\}\; \backslash \; left\; [\backslash \; left\; (\backslash \; sigma\; ^\; \{2\}\; -1\; \backslash \; right)\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Phi\}\; \{\backslash \; partial\; \backslash \; sigma\}\}\; \backslash \; right]\; +\; \{\; \backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; tau\}\}\; \backslash \; left\; [(1-\; \backslash \; tau\; ^\; \{2\})\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Phi\}\; \{\backslash \; partial\; \backslash \; tau\}\}\; \backslash \; right]\; \backslash \; right\; \backslash \}\; \backslash \; \backslash \; \{\}\; +\; \{\backslash \; frac\; \{1\}\; \{a\; ^\; \{2\}\; (\backslash \; sigma\; ^\; \{2\}\; -1)\; (1-\; \backslash \; tau\; ^\; \{2\})\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; Phi\}\; \{\backslash \; partial\; \backslash \; varphi\; ^\; \{2\}\}\}\; \backslash \; end\; \{align\}\}\}$

Другие дифференциальные операторы, такие как $\nabla \; \cdot \; F\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{F\}\}$и $\nabla \; \times \; F\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{F\}\}$можно выразить в координатах $(\sigma ,\; \tau )\; \{\backslash \; displaystyle\; (\backslash \; s\; igma,\; \backslash \; tau)\}$путем подстановки масштабных коэффициентов в общие формулы, найденные в ортогональных координатах.

Как и в случае с сферическими координатами, уравнение Лапласа может быть решено методом разделения переменных для получения решений в виде вытянутых сфероидальных гармоник, которые удобно использовать, когда граничные условия заданы на поверхности с постоянной вытянутой сфероидальной координатой ( Смайт, 1968).

Без соглашения об углах

• Morse PM, Feshbach H (1953). Методы теоретической физики, часть I. Нью-Йорк: МакГроу-Хилл. п. 661. Использует ξ 1 = a ch μ, ξ 2 = sin ν и ξ 3 = cos φ.
• Zwillinger D ( 1992). Справочник по интеграции. Бостон, Массачусетс: Джонс и Бартлетт. п. 114. ISBN 0-86720-293-9.То же, что и Morse Feshbach (1953), заменяя u k на ξ k.
• Smythe, WR (1968). Статическое и динамическое электричество (3-е изд.). Нью-Йорк: Макгроу-Хилл.
• Зауэр Р., Сабо I (1967). Mathematische Hilfsmittel des Ingenieurs. Нью-Йорк: Springer Verlag. п. 97. LCCN 67025285.Использует координаты ξ = ch μ, η = sin ν и φ.

Угловое соглашение

• Korn GA, Korn TM (1961). Математический справочник для ученых и инженеров. Нью-Йорк: Макгроу-Хилл. п. 177. LCCN 59014456.Корн и Корн используют координаты (μ, ν, φ), но также вводят вырожденные координаты (σ, τ, φ).
• Margenau H, Murphy GM (1956). Математика физики и химии. Нью-Йорк: Д. ван Ностранд. Стр. 180 –182. LCCN 55010911.Подобно Korn and Korn (1961), но использует широту θ = 90 ° - ν вместо широты ν.
• PH Луны, Спенсер Д.Е. (1988). «Вытянутые сфероидальные координаты (η, θ, ψ)». Справочник по теории поля, включая системы координат, дифференциальные уравнения и их решения (исправленное 2-е изд., 3-е изд.). Нью-Йорк: Springer Verlag. С. 28–30 (таблица 1.06). ISBN 0-387-02732-7.Мун и Спенсер используют условное обозначение широты θ = 90 ° - ν и переименовывают φ как ψ.

Необычное соглашение

• Ландау Л.Д., Лифшиц Е.М., Питаевский Л.П. (1984). Электродинамика сплошных сред (Том 8 из Курса теоретической физики ) (2-е изд.). Нью-Йорк: Pergamon Press. С. 19–29. ISBN 978-0-7506-2634-7.Обрабатывает вытянутые сфероидальные координаты как предельный случай общих эллипсоидальных координат. Использует координаты (ξ, η, ζ), которые имеют единицы расстояния в квадрате.

• Описание MathWorld вытянутых сфероидальных координат