Уравнения движения поршня

Движение поршня без смещения, соединенного с кривошипом через шатун (как можно найти в двигатели внутреннего сгорания ), можно выразить с помощью нескольких математических уравнений. В этой статье показано, как выводятся эти уравнения движения, и показан пример графика.

• 1 Геометрия коленчатого вала
  • 1.1 Определения
  • 1.2 ″ Угловая скорость ″
  • 1.3 Соотношение треугольника
• 2 Уравнения относительно углового положения (угловая область)
  • 2.1 Положение
  • 2.2 Скорость
  • 2.3 Ускорение
• 3 Уравнения относительно времени (временная область)
  • 3.1 Производные угловой скорости
  • 3.2 Преобразование из угловой области во временную область
  • 3.3 Положение
  • 3.4 Скорость
  • 3.5 Ускорение
  • 3.6 Масштабирование угловой скорости
• 4 Максимумы / минимумы скорости
  • 4.1 Переход через нулевую точку ускорения
  • 4.2 Угол поворота шатуна не является прямым
  • 4.3 Пример
• 5 Пример графика движение поршня
• 6 См. также
• 7 Ссылки
• 8 Дополнительная литература
• 9 Внешние ссылки

Диаграмма, показывающая геометрическое расположение поршневого пальца, кривошипного пальца и центра кривошипа

Определения

$l\; \{\backslash \; displaystyle\; l\}$длина штока (расстояние между поршневым пальцем и коленчатым пальцем ).

$r\; \{\backslash \; displaystyle\; r\}$кривошипом радиус (расстояние между кривошипом p в и центр кривошипа, т.е. половина хода ).

$A\; \{\backslash \; displaystyle\; A\}$угол поворота коленчатого вала (от цилиндра осевой линии отверстия в ВМТ ).

$x\; \{\backslash \; displaystyle\; x\}$положение поршневого пальца (вверх от центра кривошипа по средней линии отверстия цилиндра).

$v\; \{\backslash \; displaystyle\; v\}$скорость поршневого пальца ( вверх от центра кривошипа по средней линии отверстия цилиндра).

$a\; \{\backslash \; displaystyle\; a\}$ускорение поршневого пальца (вверх от центра кривошипа по средней линии отверстия цилиндра).

$\omega \; \{\backslash \; displaystyle\; \backslash \; omega\}$коленчатый вал угловая скорость

″ угловая скорость ″

коленчатый вал угловая скорость относится к двигателю оборотов в минуту (об / мин):

$\omega \; =\; 2\; \pi \; \cdot \; об\; /\; мин\; 60\; \{\backslash \; displaystyle\; \backslash \; omega\; =\; \{\backslash \; frac\; \{2\; \backslash \; pi\; \backslash \; cdot\; \backslash \; mathrm\; \{RPM\}\}\; \{60\}\}\}$

отношение треугольника

Как показано на схеме, шатун, центр кривошипа и поршневой палец образуют треугольник NOP.. По закону косинуса видно, что:.

$l\; 2\; =\; r\; 2\; +\; x\; 2\; -\; 2\; \cdot \; r\; \cdot \; x\; \cdot \; cos\; \; A\; \{\backslash \; displ\; aystyle\; l\; ^\; \{2\}\; =\; r\; ^\; \{2\}\; +\; x\; ^\; \{2\}\; -2\; \backslash \; cdot\; r\; \backslash \; cdot\; x\; \backslash \; cdot\; \backslash \; cos\; A\}$

Следующие уравнения описывают возвратно-поступательное движение поршня относительно угла поворота коленчатого вала.. Примеры графиков этих уравнений показаны ниже.

Положение

Положение относительно угла поворота коленчатого вала (путем изменения соотношения треугольника):

$l\; 2\; -\; r\; 2\; =\; x\; 2\; -\; 2\; \cdot \; r\; \cdot \; x\; \cdot \; cos\; \; A\; \{\backslash \; displaystyle\; l\; ^\; \{2\}\; -r\; ^\; \{2\}\; =\; x\; ^\; \{2\}\; -2\; \backslash \; cdot\; r\; \backslash \; cdot\; x\; \backslash \; cdot\; \backslash \; cos\; A\}$

$l\; 2\; -\; r\; 2\; =\; x\; 2\; -\; 2\; \cdot \; r\; \cdot \; x\; \cdot \; соз\; \; A\; +\; р\; 2\; [(соз\; 2\; \; A\; +\; грех\; 2\; \; A)\; -\; 1]\; \{\backslash \; displaystyle\; l\; ^\; \{2\}\; -r\; ^\; \{2\}\; =\; x\; ^\; \{2\}\; -2\; \backslash \; cdot\; r\; \backslash \; cdot\; x\; \backslash \; cdot\; \backslash \; cos\; A\; +\; r\; ^\; \{2\}\; [(\backslash \; cos\; ^\; \{2\}\; A\; +\; \backslash \; sin\; ^\; \{2\}\; A)\; -1]\}$

$l\; 2\; -\; r\; 2\; +\; r\; 2\; -\; r\; 2\; sin\; 2\; \; A\; =\; Икс\; 2\; -\; 2\; \cdot \; р\; \cdot \; Икс\; \cdot \; соз\; \; A\; +\; r\; 2\; соз\; 2\; \; A\; \{\backslash \; displaystyle\; l\; ^\; \{2\}\; -r\; ^\; \{2\}\; +\; r\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\; \}\; A\; =\; x\; ^\; \{2\}\; -2\; \backslash \; cdot\; r\; \backslash \; cdot\; x\; \backslash \; cdot\; \backslash \; cos\; A\; +\; r\; ^\; \{2\}\; \backslash \; cos\; ^\; \{2\}\; A\}$

$l\; 2\; -\; r\; 2\; sin\; 2\; \; A\; =\; (x\; -\; р\; \cdot \; соз\; \; A)\; 2\; \{\backslash \; displaystyle\; l\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\}\; A\; =\; (xr\; \backslash \; cdot\; \backslash \; cos\; A)\; ^\; \{2\}\}$

$x\; -\; r\; \cdot \; соз\; \; A\; =\; l\; 2\; -\; r\; 2\; грех\; 2\; \; A\; \{\backslash \; displaystyle\; xr\; \backslash \; cdot\; \backslash \; cos\; A\; =\; \{\backslash \; sqrt\; \{l\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\}\; A\}\}\}$

$Икс\; знак\; равно\; г\; \cdot \; соз\; \; А\; +\; l\; 2\; -\; г\; 2\; грех\; 2\; \; А.\; \{\backslash \; displaystyle\; x\; =\; r\; \backslash \; cdot\; \backslash \; cos\; A\; +\; \{\backslash \; sqrt\; \{l\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\}\; A\}\}.\}$

Скорость

Скорость относительно до угла поворота коленчатого вала (возьмите первую производную, используя цепное правило ):

$x\; \prime \; =\; dxd\; A\; =\; -\; r\; sin\; \; A\; +\; (1\; 2).\; (-\; 2).\; r\; 2\; sin\; \; A\; cos\; \; A\; l\; 2\; -\; r\; 2\; sin\; 2\; \; A\; =\; -\; r\; sin\; \; A\; (1\; +\; r\; cos\; \; A\; l\; 2\; -\; r\; 2\; sin\; 2\; \; A).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{lcl\}\; x\; \text{'}=\; \{\backslash \; frac\; \{dx\}\; \{dA\}\}\; \backslash \backslash \; =\; -\; r\; \backslash \; sin\; A\; +\; \{\backslash \; frac\; \{(\{\backslash \; frac\; \{1\}\; \{2\; \}\}).\; (-\; 2).r\; ^\; \{2\}\; \backslash \; sin\; A\; \backslash \; cos\; A\}\; \{\backslash \; sqrt\; \{l\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\}\; A\}\}\}\; \backslash \backslash \; =\; -r\; \backslash \; sin\; A\; \backslash \; left\; (1\; +\; \{\backslash \; frac\; \{r\; \backslash \; cos\; A\}\; \{\backslash \; sqrt\; \{l\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\}\; A\}\}\}\; \backslash \; right).\; \backslash \; end\; \{array\}\}\}$

Скорость отрицательна, когда x уменьшается со временем (A < 180 degrees) and is positive when x increases with time(A>180 градусов). Величина второго члена всегда меньше rsinA и, следовательно, не влияет на знак (так как l>= 2 * r).

Acceleration

Ускорение относительно угла поворота коленчатого вала (возьмите секунду производная, используя правило цепочки и правило частного ):

$x ″ = d 2 xd A 2 = - r cos ⁡ A - r 2 cos 2 ⁡ A l 2 - r 2 sin 2 ⁡ A - - r 2 sin 2 ⁡ A l 2 - r 2 sin 2 ⁡ A - r 2 sin ⁡ A cos ⁡ A. (- 1 2) ⋅ (- 2). r 2 sin ⁡ A cos ⁡ A (l 2 - r 2 sin 2 ⁡ A) 3 = - r cos ⁡ A - r 2 (cos 2 ⁡ A - sin 2 ⁡ A) l 2 - r 2 sin 2 ⁡ A - r 4 sin 2 ⁡ A cos 2 ⁡ A (l 2 - r 2 sin 2 ⁡ A) 3 = r (r (l 2 (sin 2 ⁡ A - cos 2 ⁡ A) - r 2 sin 4 ⁡ A) (l 2 - r 2 sin 2 ⁡ A) 3/2 - cos A). {\ displaystyle {\ begin {array} {lcl} x '' = {\ frac {d ^ {2} x} {dA ^ {2}}} \\ = - r \ cos A - {\ frac {r ^ {2} \ cos ^ {2} A} {\ sqrt {l ^ {2} -r ^ {2} \ sin ^ {2} A}}} - {\ frac {-r ^ {2 } \ sin ^ {2} A} {\ sqrt {l ^ {2} -r ^ {2} \ sin ^ {2} A}}} - {\ frac {r ^ {2} \ sin A \ cos A. \ left (- {\ frac {1} {2}} \ right) \ cdot (-2).r ^ {2} \ sin A \ cos A} {\ left ({\ sqrt {l ^ {2}) -r ^ {2} \ sin ^ {2} A}} \ right) ^ {3}}} \\ = - r \ cos A - {\ frac {r ^ {2} \ left (\ cos ^ {2} A- \ sin ^ {2} A \ right)} {\ sqrt {l ^ {2} -r ^ {2} \ sin ^ {2} A}}} - {\ frac {r ^ {4 } \ sin ^ {2} A \ cos ^ {2} A} {\ left ({\ sqrt {l ^ {2} -r ^ {2} \ sin ^ {2} A}} \ right) ^ {3 }}} \\ = r \ left ({\ frac {r \ left (l ^ {2} \ left (\ sin ^ {2} A- \ cos ^ {2} A \ right) -r ^ {2 } \ sin ^ {4} A \ right)} {\ left (l ^ {2} -r ^ {2} \ sin ^ {2} A \ right) ^ {3/2}}} - \ cos A \ справа). \ end {array}}}$

Производные угловой скорости

Если угловая скорость постоянна, то

$A\; =\; \omega \; t\; \{\backslash \; displaystyle\; A\; =\; \backslash \; omega\; t\; \backslash ,\}$

и применяются следующие соотношения:

$d\; A\; dt\; =\; \omega \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dA\}\; \{dt\}\}\; =\; \backslash \; omega\}$

$d\; 2\; A\; dt\; 2\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; A\}\; \{dt\; ^\; \{\; 2\}\}\}\; =\; 0\}$

Преобразование из угловой области во временную область

Следующие уравнения описывают возвратно-поступательное движение поршня во времени. Если вместо угловой области требуется временная область, сначала замените A на ωt в уравнениях, а затем scale для угловой скорости следующим образом:

Position

Положение относительно времени просто:

$x\; \{\backslash \; displaystyle\; x\; \backslash ,\}$

Скорость

Скорость относительно времени (с использованием правила цепочки ):

$v\; =\; dxdt\; =\; dxd\; A\; \cdot \; d\; A\; dt\; =\; dxd\; A\; \cdot \; \omega \; =\; x\; \prime \; \cdot \; \omega \; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{lcl\}\; v\; =\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{dx\}\; \{dA\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{dA\}\; \{dt\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{dx\}\; \{dA\}\}\; \backslash \; cdot\; \backslash \; \backslash \; omega\; \backslash \backslash \; =\; x\; \text{'}\backslash \; cdot\; \backslash \; omega\; \backslash \backslash \backslash \; end\; \{array\}\}\}$

Ускорение

Ускорение по времени (с использованием правила цепочки и правила продукта, и производные угловой скорости ):

$a\; =\; d\; 2\; xdt\; 2\; =\; ddtdxdt\; =\; ddt\; (dxd\; A\; \cdot \; d\; A\; dt)\; =\; ddt\; (dxd\; A)\; \cdot \; d\; A\; dt\; +\; dxd\; A\; \cdot \; ddt\; (\; d\; A\; dt)\; =\; dd\; A\; (dxd\; A)\; \cdot \; (d\; A\; dt)\; 2\; +\; dxd\; A\; \cdot \; d\; 2\; A\; dt\; 2\; =\; d\; 2\; xd\; A\; 2\; \cdot \; (d\; A\; dt)\; 2\; +\; dxd\; A\; \cdot \; d\; 2\; A\; dt\; 2\; =\; d\; 2\; xd\; A\; 2\; \cdot \; \omega \; 2\; +\; dxd\; A\; \cdot \; 0\; =\; x\; ″\; \cdot \; \omega \; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{lcl\}\; a\; =\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; x\}\; \{dt\; ^\; \{2\}\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; (\{\backslash \; frac\; \{dx\}\; \{dA\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{\; dA\}\; \{dt\}\})\; \backslash \backslash \; =\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; (\{\backslash \; frac\; \{dx\}\; \{dA\}\})\; \backslash \; cdot\; \{\backslash \; frac\; \{dA\}\; \{dt\}\}\; +\; \{\backslash \; frac\; \{dx\}\; \{dA\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; (\{\backslash \; frac\; \{dA\}\; \{dt\}\})\; \backslash \backslash \; =\; \{\backslash \; frac\; \{d\}\; \{dA\}\}\; (\{\backslash \; frac\; \{dx\}\; \{dA\}\})\; \backslash \; cdot\; (\{\backslash \; frac\; \{dA\}\; \{dt\}\})\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{dx\}\; \{dA\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; A\}\; \{dt\; ^\; \{2\}\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; x\}\; \{dA\; ^\; \{2\}\}\}\; \backslash \; cdot\; (\{\backslash \; frac\; \{dA\}\; \{dt\}\})\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{dx\}\; \{dA\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; A\}\; \{dt\; ^\; \{2\}\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; x\}\; \{dA\; ^\; \{2\}\}\}\; \backslash \; cdot\; \backslash \; omega\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{dx\}\; \{dA\}\}\; \backslash \; cdot\; 0\; \backslash \backslash \; =\; x\; \text{'}\text{'}\; \backslash \; cdot\; \backslash \; omega\; ^\; \{2\}\; \backslash \backslash \backslash \; end\; \{array\}\; \}\}$

Масштабирование угловой скорости

Вы можете видеть, что x не масштабируется, x 'масштабируется на ω, а x "масштабируется на ω². Чтобы преобразовать x 'из скорости в зависимости от угла [дюйм / рад] в скорость в зависимости от времени [дюйм / с], умножьте x' на ω [рад / с]. Чтобы преобразовать x "из ускорения в зависимости от угла [дюйм / рад²] в ускорение в зависимости от времени [дюйм / с²], умножьте x» на ω² [рад² / с²]. Обратите внимание, что анализ размеров показывает, что единицы согласованы.

Переходы через ноль ускорения

Максимумы и минимумы скорости не возникают при углах поворота коленчатого вала (A) плюс или минус 90 °. Максимумы и минимумы скорости возникают при углах поворота коленчатого вала, которые зависят от длины штока (l) и половины хода (r), и соответствуют углам поворота коленчатого вала, где ускорение равно нулю (пересечение горизонтальной оси).

Угол поворота кривошипа неправильный

Максимумы и минимумы скорости не обязательно возникают, когда кривошип находится под прямым углом к ​​штоку. Существуют контрпримеры, чтобы опровергнуть идею о том, что максимумы / минимумы скорости возникают, когда угол поворота коленчатого вала является прямым.

Пример

Для длины штока 6 дюймов и радиуса кривошипа 2 дюйма численное решение пересечений нуля ускорения обнаруживает, что максимумы / минимумы скорости находятся при углах поворота кривошипа ± 73,17615 °. Затем, используя закон синусоидального треугольника, можно найти, что угол поворота шатуна составляет 88,21738 °, а угол стержня по вертикали равен 18,60647 °. Очевидно, что в этом примере угол между кривошипом и стержнем не является прямым. Суммируя углы треугольника 88,21738 ° + 18,60647 ° + 73,17615 °, получаем 180,00000 °. Единственного контрпримера достаточно, чтобы опровергнуть утверждение «максимумы / минимумы скорости возникают, когда кривошип делает прямой угол со штоком».

На графике показаны x, x ', x "относительно угла поворота коленчатого вала для различных половин хода, где L = длина штока (l) и R = половина хода (r):

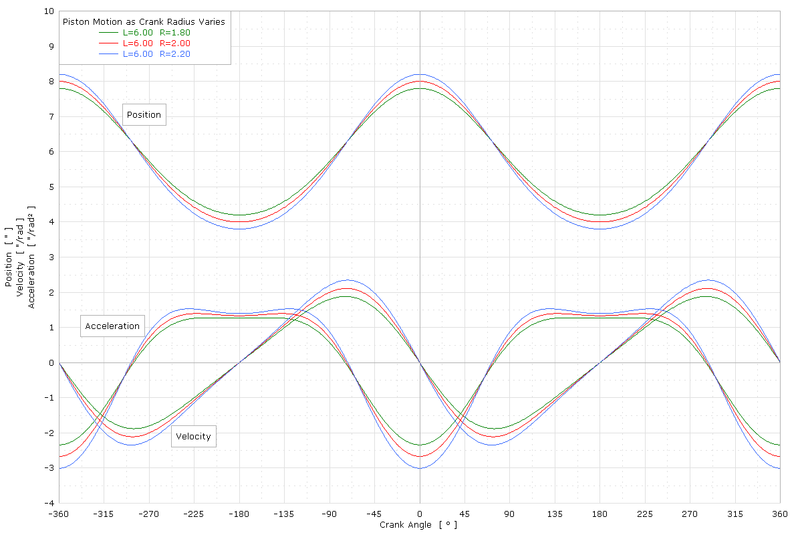
Единицы измерения по вертикальной оси: дюймы для положения, [дюймы / рад] для скорости, [дюймы / рад²] для ускорения.. Единицы измерения по горизонтальной оси - угол поворота коленчатого вала градусов.

Анимация движения поршня с одинаковыми значениями длины штока и радиуса кривошипа на графике выше:.

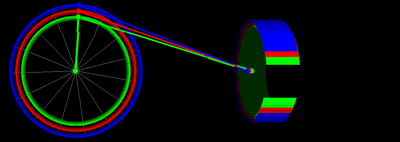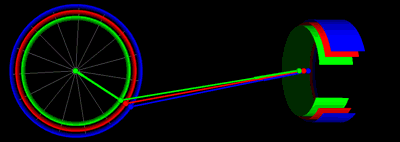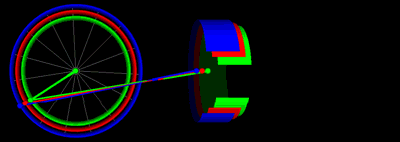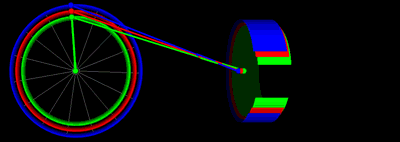
Анимация движения поршня с различными половинными ходами

• Двигатель внутреннего сгорания
• Поршневой двигатель
• Ползунок -кривошип
• Хомут

• http://www.epi-eng.com/piston_engine_technology/piston_motion_basics.htm

• Джон Бенджамин Хейвуд, Основы двигателя внутреннего сгорания, McGraw Hill, 1989.
• Чарльз Файетт Тейлор, Двигатель внутреннего сгорания в теории и практике, том 1 и 2, 2-е издание, MIT Press, 1985.

• epi-eng Код движения поршня
• cogs Скорость и ускорение поршня
• Анимированные двигатели Четырехтактный двигатель
• desmos интерактивная анимация кривошипа
• networcs Механизмы DT - Интерактивные инструменты для учителей
• mecamedia Анимация движения поршня

• youtube Вращающийся короткий блок chevy 350.
• youtube 3D-анимация ДВИГАТЕЛЯ V8
• youtube Внутри двигателя V8 на холостом ходу
• desmos интерактивный ход в зависимости от соотношения штока и положения поршня