Распределение Ирвина – Холла

Распределение Ирвина – Холла

Функция плотности вероятности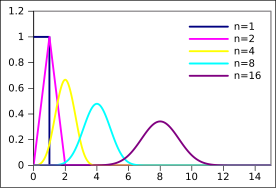
Кумулятивная функция распределения
Параметры	n ∈ N0
Поддержка	$x\; \in \; [\; 0,\; n]\; \{\backslash \; displaystyle\; x\; \backslash \; in\; [0,\; n]\}$
PDF	$1\; (n\; -\; 1)!\; \sum \; К\; знак\; равно\; 0\; \lfloor \; Икс\; \rfloor \; (-\; 1)\; К\; (NK)\; (Икс\; -\; К)\; N\; -\; 1\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{1\}\; \{(п-1)!\}\}\; \backslash \; Sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; lfloor\; x\; \backslash \; rfloor\}\; (-\; 1)\; ^\; \{k\}\; \{\backslash \; binom\; \{n\}\; \{k\}\}\; (xk)\; ^\; \{n-1\}\}$
CDF	$1\; n!\; \sum \; К\; знак\; равно\; 0\; \lfloor \; Икс\; \rfloor \; (-\; 1)\; К\; (NK)\; (Икс\; -\; К)\; N\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{1\}\; \{n!\}\}\; \backslash \; Sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; lfloor\; x\; \backslash \; rfloor\; \}\; (-\; 1)\; ^\; \{k\}\; \{\backslash \; binom\; \{n\}\; \{k\}\}\; (xk)\; ^\; \{n\}\}$
Среднее	$n\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{n\}\; \{2\}\}\}$
Медиана	$n\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{n\}\; \{2\}\}\}$
Mode	$\{любое\; значение\; в\; [0,\; 1]\; для\; n\; =\; 1\; n\; 2\; в\; противном\; случае\; \{\backslash \; displaystyle\; \{\; \backslash \; begin\; \{cases\}\; \{\backslash \; text\; \{любое\; значение\; в\}\}\; [0,1]\; \{\backslash \; text\; \{for\}\}\; n\; =\; 1\; \backslash \backslash \; \{\backslash \; frac\; \{n\}\; \{2\}\}\; \{\backslash \; text\; \{иначе\}\}\; \backslash \; end\; \{cases\}\}\}$
Дисперсия	$n\; 12\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{n\}\; \{12\}\}\}$
Асимметрия	0
Пример. эксцесс	$-\; 6\; 5\; n\; \{\backslash \; displaystyle\; -\; \{\backslash \; tfrac\; \{6\}\; \{5n\}\}\}$
MGF	$(et\; -\; 1\; t)\; n\; \{\backslash \; displaystyle\; \{\backslash \; left\; (\{\backslash \; frac\; \{\backslash \; mathrm\; \{e\}\; ^\; \{t\}\; -1\}\; \{t\}\}\; \backslash \; right)\}\; ^\; \{n\}\}$
CF	$(eit\; -\; 1\; it)\; n\; \{\backslash \; displaystyle\; \{\backslash \; left\; (\{\backslash \; frac\; \{\backslash \; mathrm\; \{e\}\; ^)\; \{it\}\; -1\}\; \{it\}\}\; \backslash \; right)\}\; ^\; \{n\}\}$

В вероятности и статистике, распределение Ирвина – Холла, названный в честь Джозефа Оскара Ирвина и Филиппа Холла, представляет собой распределение вероятностей для случайной величины, определяемой как сумма ряда независимые случайные величины, каждая из которых имеет равномерное распределение. По этой причине оно также известно как равномерное распределение суммы .

. Генерация псевдослучайных чисел, имеющих приблизительно нормальное распределение, иногда достигается путем вычисления суммы ряд псевдослучайных чисел, имеющих равномерное распределение; обычно ради простоты программирования. Изменение масштаба распределения Ирвина – Холла обеспечивает точное распределение генерируемых случайных величин.

Это распределение иногда путают с распределением Бейтса, которое является средним (не суммой ) n независимых случайных величин, равномерно распределенных из От 0 до 1.

• 1 Определение
• 2 Особые случаи
• 3 Подобные и родственные распределения
• 4 Расширения к распределению Ирвина – Холла
• 5 См. Также
• 6 Примечания
• 7 Ссылки

Распределение Ирвина – Холла - это непрерывное распределение вероятностей для суммы n независимых и одинаково распределенных U ( 0, 1) случайные величины:

$X\; =\; \sum \; k\; =\; 1\; n\; U\; k.\; \{\backslash \; displaystyle\; X\; =\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; U\_\; \{k\}.\}$

Функция плотности вероятности (pdf) определяется как

$f\; X\; (x;\; п)\; =\; 1\; 2\; (п\; -\; 1)!\; \sum \; К\; знак\; равно\; 0\; N\; (-\; 1)\; К\; (NK)\; (Икс\; -\; К)\; N\; -\; 1\; знак\; \; (Икс\; -\; К)\; \{\backslash \; Displaystyle\; F\_\; \{X\}\; (х;\; п)\; =\; \{\backslash \; гидроразрыва\; \{1\}\; \{2\; (\; n-1)!\}\}\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{n\}\; (-\; 1)\; ^\; \{k\}\; \{n\; \backslash \; choose\; k\}\; (xk)\; ^\; \{n-1\}\; \backslash \; operatorname\; \{sgn\}\; (xk)\; \}$

где sgn (x - k) обозначает знаковую функцию :

Таким образом, pdf представляет собой сплайн (кусочно-полиномиальная функция) степени n - 1 над узлами 0, 1,..., n. Фактически, для x между узлами, расположенными в k и k + 1, pdf равно

$е\; Икс\; (Икс;\; N)\; знак\; равно\; 1\; (N\; -\; 1)!\; \sum \; J\; =\; 0\; N\; -\; 1\; aj\; (K,\; N)\; XJ\; \{\backslash \; Displaystyle\; F\_\; \{X\}\; (х;\; п)\; =\; \{\backslash \; гидроразрыва\; \{1\}\; \{(\; n-1)!\}\}\; \backslash \; sum\; \_\; \{j\; =\; 0\}\; ^\; \{n-1\}\; a\_\; \{j\}\; (k,\; n)\; x\; ^\; \{j\}\}$

где коэффициенты a j (k, n) можно найти из рекуррентного соотношения по k

Компания эффективными также являются A188816 в OEIS. Коэффициенты для кумулятивного распределения равны A188668.

. Среднее значение и дисперсия равны n / 2 и n / 12 соответственно.

• Для n = 1 X следует равномерному распределению :

$f\; X\; (x)\; =\; \{1\; 0\; \le \; x\; \le \; 1\; 0\; в\; противном\; случае\; \{\backslash \; displaystyle\; f\_\; \{X\}\; (\; x)\; =\; \{\backslash \; begin\; \{cases\}\; 1\; 0\; \backslash \; leq\; x\; \backslash \; leq\; 1\; \backslash \backslash \; 0\; \{\backslash \; text\; \{else\}\}\; \backslash \; end\; \{cases\}\}\}$

• Для n = 2 X следует треугольному распределению :

$е\; Икс\; (Икс)\; =\; \{Икс\; 0\; \le \; Икс\; \le \; 1\; 2\; -\; Икс\; 1\; \le \; Икс\; \le \; 2\; \{\backslash \; Displaystyle\; F\_\; \{X\}\; (x)\; =\; \{\backslash \; begin\; \{cases\}\; x\; 0\; \backslash \; Leq\; x\; \backslash \; Leq\; 1\; \backslash \backslash \; 2\; -x\; 1\; \backslash \; leq\; x\; \backslash \; leq\; 2\; \backslash \; end\; \{ases\}\}$

• Для n = 3,

$f\; X\; (x)\; =\; \{1\; 2\; x\; 2\; 0\; \le \; x\; \le \; 1\; 1\; 2\; (-\; 2\; x\; 2\; +\; 6\; x\; -\; 3)\; 1\; \le \; x\; \le \; 2\; 1\; 2\; (x\; -\; 3)\; 2\; 2\; \le \; x\; \le \; 3\; \{\backslash \; displaystyle\; f\_\; \{X\}\; (x)\; =\; \{\backslash \; begin\; \{cases\}\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; x\; ^\; \{2\}\; 0\; \backslash \; leq\; x\; \backslash \; leq\; 1\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (-\; 2x\; ^\; \{2\}\; +\; 6x-3)\; 1\; \backslash \; leq\; x\; \backslash \; leq\; 2\; \backslash \backslash \; \{\backslash \; frac\; \{1\; \}\; \{2\}\}\; (x-3)\; ^\; \{2\}\; 2\; \backslash \; leq\; x\; \backslash \; leq\; 3\; \backslash \; end\; \{cases\}\}\}$

• Для n = 4,

$f\; X\; (x)\; =\; \{1\; 6\; x\; 3\; 0\; \le \; x\; \le \; 1\; 1\; 6\; (-\; 3\; x\; 3\; +\; 12\; x\; 2\; -\; 12\; x\; +\; 4)\; 1\; \le \; x\; \le \; 2\; 1\; 6\; (3\; x\; 3\; -\; 24\; x\; 2\; +\; 60\; x\; -\; 44)\; 2\; \le \; x\; \le \; 3\; 1\; 6\; (-\; x\; +\; 4)\; 3\; 3\; \le \; x\; \le \; 4\; \{\backslash \; displaystyle\; f\_\; \{X\}\; (x)\; =\; \{\backslash \; begin\; \{cases\}\; \{\backslash \; frac\; \{1\}\; \{6\}\}\; x\; ^\; \{3\}\; 0\; \backslash \; leq\; x\; \backslash \; leq\; 1\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{6\}\}\; (-\; 3x\; ^\; \{3\}\; +\; 12x\; ^\; \{2\}\; -12x\; +\; 4)\; 1\; \backslash \; leq\; x\; \backslash \; leq\; 2\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{6\}\}\; (3x\; ^\; \{3\}\; -24x\; ^\; \{2\}\; +\; 60x-44)\; 2\; \backslash \; leq\; x\; \backslash \; leq\; 3\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{6\}\}\; (-\; x\; +\; 4)\; ^\; \{3\}\; 3\; \backslash \; leq\; x\; \backslash \; leq\; 4\; \backslash \; end\; \{case\}\}\; \}$

• Для n = 5,

$f\; X\; (x)\; =\; \{1\; 24\; x\; 4\; 0\; \le \; x\; \le \; 1\; 1\; 24\; (-\; 4\; x\; 4\; +\; 20\; x\; 3\; -\; 30\; x\; 2\; +\; 20\; x\; -\; 5)\; 1\; \le \; x\; \le \; 2\; 1\; 24\; (6\; x\; 4\; -\; 60\; x\; 3\; +\; 210\; x\; 2\; -\; 300\; x\; +\; 155)\; 2\; \le \; x\; \le \; 3\; 1\; 24\; (-\; 4\; x\; 4\; +\; 60\; x\; 3\; -\; 330\; x\; 2\; +\; 780\; x\; -\; 655)\; 3\; \le \; x\; \le \; 4\; 1\; 24\; (x\; -\; 5)\; 4\; 4\; \le \; x\; \le \; 5\; \{\backslash \; displaystyle\; f\_\; \{X\}\; (x)\; =\; \{\backslash \; begin\; \{cases\}\; \{\backslash \; frac\; \{1\}\; \{24\}\}\; x\; ^\; \{4\}\; 0\; \backslash \; leq\; x\; \backslash \; leq\; 1\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{24\}\}\; (-\; 4x\; ^\; \{4\}\; +\; 20x\; ^\; \{3\}\; -30x\; ^\; \{2\}\; +\; 20x-5)\; 1\; \backslash \; leq\; x\; \backslash \; leq\; 2\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{24\}\}\; (6x\; ^\; \{4\}\; -60x\; ^\; \{3\}\; +\; 210x\; ^\; \{2\}\; -300x\; +\; 155)\; 2\; \backslash \; leq\; x\; \backslash \; leq\; 3\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{24\}\}\; (-\; 4x\; ^\; \{4\}\; +\; 60x\; ^\; \{3\}\; -330x\; ^\; \{2\}\; +\; 780x-655)\; 3\; \backslash \; leq\; x\; \backslash \; leq\; 4\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{24\}\}\; (x-\; 5)\; ^\; \{4\}\; 4\; \backslash \; leq\; x\; \backslash \; leq\; 5\; \backslash \; end\; \{cases\}\}\}$

Распределение Ирвина – Холла аналогично распределению Бейтса, но по-прежнему с целыми числами в качестве параметра. Расширение до параметров с действительным знаком возможно путем добавления случайной однородной переменной с N - trunc (N) в качестве ширины.

При использовании Ирвина – Холла для подбора данных одна проблема заключается в том, что IH не очень гибок, поскольку параметр n должен быть целым числом. Однако вместо суммирования n равных равномерных распределений мы могли бы также добавить, например, U + 0,5U также для случая n = 1,5 (что дает трапециевидное распределение).

• Распределение Бейтса
• Нормальное распределение
• Центральная предельная теорема
• Равномерное распределение (непрерывное)
• Треугольное распределение

• Холл, Филипп. (1927) «Распределение средних значений для выборок размера N, взятых из популяции, в которой переменная принимает значения от 0 до 1, все такие значения равновероятны». Биометрика, Vol. 19, № 3/4., С. 240–245. doi :10.1093/biomet/19.3-4.240 JSTOR 2331961
• Ирвин, Дж. (1927) «О частотном распределении средних значений выборок из популяции, имеющей любой закон частоты с конечными моментами, с особым упором на тип II Пирсона». Биометрика, Vol. 19, № 3/4., Стр. 225–239. doi :10.1093/biomet/19.3-4.225 JSTOR 2331960