Общий кадр

редактировать

В логике , общие кадры (или просто кадры ) - это фреймы Крипке с дополнительной структурой, которые используются для моделирования модальной и промежуточной логики. Общая семантика фрейма сочетает в себе основные достоинства семантики Крипке и алгебраической семантики : она разделяет прозрачное геометрическое понимание первой и надежную полноту последней.

Содержание

1 Определение
2 Типы фреймов
3 Операции и морфизмы над фреймами
4 Полнота
5 Двойственность Йонссона – Тарского
6 Интуиционистские фреймы
7 Ссылки

Определение

A модальный общий фрейм - это тройка $F = ⟨F, R, V⟩ {\ displaystyle \ mathbf {F} = \ langle F, R, V \ rangle}$ ${\ mathbf F} = \ langle F, R, V \ rangle$ , где $⟨F, R⟩ {\ displaystyle \ langle F, R \ rangle}$ ${\ displaystyle \ langle F, R \ rangle}$ - фрейм Крипке (т. Е. R - двоичное отношение на множестве F), а V - это набор подмножеств F, который замкнут при следующих условиях:

булевы операции (двоичного) пересечения, union и дополнения,
операция $◻ {\ displaystyle \ Box}$ $\ Box$ , определенная как $◻ A = {x ∈ F; ∀ Y ∈ F (Икс R Y → Y ∈ A)} {\ Displaystyle \ Box A = \ {x \ in F; \, \ forall y \ in F \, (x \, R \, y \ to y \ в A) \}}$ ${\ displaystyle \ Box A = \ {x \ in F; \, \ forall y \ in F \, (x \, R \, y \ to y \ in A) \}}$ .

Таким образом, они являются частным случаем полей наборов с дополнительной структурой. Цель V - ограничить допустимые оценки во фрейме: модель $⟨F, R, ⊩⟩ {\ displaystyle \ langle F, R, \ Vdash \ rangle}$ ${\ displaystyle \ langle F, R, \ Vdash \ rangle}$ на основе модели Крипке кадр $⟨F, R⟩ {\ displaystyle \ langle F, R \ rangle}$ ${\ displaystyle \ langle F, R \ rangle}$ является допустимым в общем кадре F, если

{x ∈ F; x ⊩ p} ∈ V {\ displaystyle \ {x \ in F; \, x \ Vdash p \} \ in V}

{\ displaystyle \ {x \ in F; \, x \ Vdash p \ } \ in V}

для каждой пропозициональной переменной p.

. Условия замыкания на V, тогда убедитесь, что ${x ∈ F; x ⊩ A} {\ displaystyle \ {x \ in F; \, x \ Vdash A \}}$ ${\ displaystyle \ {x \ in F; \, x \ Vdash A \}}$ принадлежит V для каждой формулы A (не только переменной).

Формула A действительна в F, если $x ⊩ A {\ displaystyle x \ Vdash A}$ ${\ displaystyle x \ Vdash A}$ для всех допустимых оценки $⊩ {\ Displaystyle \ Vdash}$ $\ Vdash$ , и все точки $x ∈ F {\ displaystyle x \ in F}$ $x \ in F$ . нормальная модальная логика L действительна в кадре F, если все аксиомы (или, что эквивалентно, все теоремы) L действительны в F . В этом случае мы называем F рамкой L- .

рамкой Крипке $⟨F, R⟩ {\ displaystyle \ langle F, R \ rangle}$ ${\ displaystyle \ langle F, R \ rangle}$ может быть отождествлен с общим фреймом, в котором допустимы все оценки: т. е. $⟨F, R, P (F)⟩ {\ displaystyle \ langle F, R, {\ mathcal {P}} (F) \ rangle }$ ${\ displaystyle \ langle F, R, {\ mathcal {P}} (F) \ rangle}$ , где $P (F) {\ displaystyle {\ mathcal {P}} (F)}$ ${\ displaystyle {\ mathcal {P}} (F)}$ обозначает набор мощности F.

Типы рамок

В общем, общие рамки - это не более чем причудливое название для моделей Крипке; в частности, теряется соответствие модальных аксиом свойствам отношения доступности. Это можно исправить, наложив дополнительные условия на множество допустимых оценок.

Рамка $F = ⟨F, R, V⟩ {\ displaystyle \ mathbf {F} = \ langle F, R, V \ rangle}$ ${\ mathbf F} = \ langle F, R, V \ rangle$ называется

дифференцированный, если $∀ A ∈ V (x ∈ A ⇔ y ∈ A) {\ displaystyle \ forall A \ in V \, (x \ in A \ Leftrightarrow y \ in A)}$ ${\ displaystyle \ forall A \ in V \, (x \ in A \ Leftrightarrow y \ in A)}$ подразумевает $x = y {\ displaystyle x = y}$ $x = y$ ,
плотно, если $∀ A ∈ V (x ∈ ◻ A ⇒ y ∈ A) {\ displaystyle \ forall A \ in V \, (x \ in \ Box A \ Rightarrow y \ in A)}$ ${\ displaystyle \ forall A \ in V \, (x \ in \ Box A \ Rightarrow y \ in A)}$ подразумевает $x R y {\ displaystyle x \, R \, y}$ ${\ displaystyle x \, R \, y}$ ,
компактный, если каждое подмножество V со свойством конечного пересечения имеет непустое пересечение,
атомарное, если V содержит все синглтоны,
уточненный, если он дифференцирован и плотный,
описательный,, если он изящный и компактный.

Фреймы Крипке изящны и атомарны. Однако бесконечные рамки Крипке никогда не бывают компактными. Каждая конечная дифференцированная или атомарная система отсчета является шкалой Крипке.

Описательные фреймы являются наиболее важным классом фреймов из-за теории двойственности (см. Ниже). Уточненные фреймы полезны как общее обобщение описательных фреймов и фреймов Крипке.

Операции и морфизмы на фреймах

Каждая модель Крипке $⟨F, R, ⊩⟩ {\ displaystyle \ langle F, R, {\ Vdash} \ rangle}$ ${\ displaystyle \ langle F, R, {\ Vdash} \ rangle}$ индуцирует общий фрейм $⟨F, R, V⟩ {\ displaystyle \ langle F, R, V \ rangle}$ ${\ displaystyle \ langle F, R, V \ rangle}$ , где V определяется как

V = {{x ∈ F; x ⊩ A}; A - это формула}. {\ displaystyle V = {\ big \ {} \ {x \ in F; \, x \ Vdash A \}; \, A {\ hbox {- формула}} {\ big \}}.}

{\ displaystyle V = {\ big \ {} \ {x \ in F; \, x \ Vdash A \}; \, A {\ hbox {- формула}} {\ big \}}.}

Фундаментальные сохраняющие истину операции над порожденными подфреймами, p-морфическими изображениями и непересекающимися объединениями фреймов Крипке имеют аналоги на общих фреймах. Кадр $G = ⟨G, S, W⟩ {\ displaystyle \ mathbf {G} = \ langle G, S, W \ rangle}$ ${\ displaystyle \ mathbf {G} = \ langle G, S, W \ rangle}$ - это сгенерированный подкадр рамка $F = ⟨F, R, V⟩ {\ displaystyle \ mathbf {F} = \ langle F, R, V \ rangle}$ ${\ mathbf F} = \ langle F, R, V \ rangle$ , если рамка Крипке $⟨G, S⟩ {\ displaystyle \ langle G, S \ rangle}$ ${\ displaystyle \ langle G, S \ rangle}$ - сгенерированный подкадр кадра Крипке $⟨F, R⟩ {\ displaystyle \ langle F, R \ rangle}$ ${\ displaystyle \ langle F, R \ rangle}$ (т. Е. $G {\ displaystyle G}$ $G$ является подмножеством $F {\ displaystyle F}$ $F$ , закрытым вверх под $R {\ displaystyle R }$ $R$ и $S = R ∩ G × G {\ displaystyle S = R \ cap G \ times G}$ ${\ displaystyle S = R \ cap G \ times G }$ ), и

W = {A ∩ G ; A ∈ V}. {\ displaystyle W = \ {A \ cap G; \, A \ in V \}.}

{\ displaystyle W = \ {A \ cap G; \, A \ in V \}. }

A p-морфизм (или ограниченный морфизм ) $f: F → G {\ displaystyle f \ двоеточие \ mathbf {F} \ to \ mathbf {G}}$ ${\ displaystyle f \ двоеточие \ mathbf {F} \ to \ mathbf {G}}$ - это функция от F до G, которая является p-морфизмом фреймов Крипке $⟨F, R⟩ {\ displaystyle \ langle F, R \ rangle}$ ${\ displaystyle \ langle F, R \ rangle}$ и $⟨G, S⟩ {\ displaystyle \ langle G, S \ rangle}$ ${\ displaystyle \ langle G, S \ rangle}$ и удовлетворяет дополнительному ограничению

f - 1 [A] ∈ V {\ displaystyle f ^ {- 1} [A] \ in V}

{\ displaystyle f ^ {- 1} [A] \ in V}

для каждого

A ∈ W {\ displaystyle A \ in W}

{\ displaystyle A \ in W}

непересекающееся объединение индексированного набора фреймов $F i = ⟨F i, R i, V i⟩ {\ displaystyle \ mathbf {F} _ {i} = \ langle F_ {i }, R_ {i}, V_ {i} \ rangle}$ ${\ displaystyle \ mathbf {F} _ {i} = \ langle F_ {i}, R_ {i}, V_ {i} \ rangle}$ , $i ∈ I {\ displaystyle i \ in I}$ $i \ in I$ , это рамка $F = ⟨F, R, V⟩ {\ displaystyle \ mathbf {F} = \ langle F, R, V \ rangle}$ ${\ mathbf F} = \ langle F, R, V \ rangle$ , где F - несвязное объединение ${F i; i ∈ I} {\ displaystyle \ {F_ {i}; \, i \ in I \}}$ ${\ displaystyle \ {F_ {i}; \, i \ in I \}}$ , R - объединение ${R i; i ∈ I} {\ displaystyle \ {R_ {i}; \, i \ in I \}}$ ${\ displaystyle \ {R_ {i}; \, i \ in I \}}$ и

V = {A ⊆ F; ∀ i ∈ I (A ∩ F i ∈ V i)}. {\ displaystyle V = \ {A \ substeq F; \, \ forall i \ in I \, (A \ cap F_ {i} \ in V_ {i}) \}.}

{\ displaystyle V = \ {A \ substeq F; \, \ forall i \ in I \, (A \ ca p F_ {i} \ in V_ {i}) \}.}

Уточнение фрейма $F = ⟨F, R, V⟩ {\ displaystyle \ mathbf {F} = \ langle F, R, V \ rangle}$ ${\ mathbf F} = \ langle F, R, V \ rangle$ - усовершенствованный фрейм $G Знак равно ⟨G, S, W⟩ {\ displaystyle \ mathbf {G} = \ langle G, S, W \ rangle}$ ${\ displaystyle \ mathbf {G} = \ langle G, S, W \ rangle}$ определяется следующим образом. Мы рассматриваем отношение эквивалентности

x ∼ y ⟺ ∀ A ∈ V (x ∈ A ⇔ y ∈ A), {\ displaystyle x \ sim y \ iff \ forall A \ in V \, (x \ in A \ Leftrightarrow y \ in A),}

{\ displaystyle x \ sim y \ iff \ forall A \ in V \, (x \ in A \ Leftrightarrow y \ in A),}

и пусть $G = F / ∼ {\ displaystyle G = F / {\ sim}}$ ${\ displaystyle G = F / {\ sim}}$ будет набором классов эквивалентности $∼ {\ Displaystyle \ sim}$ $\ sim$ . Затем положим

⟨x / ∼, y / ∼⟩ ∈ S ⟺ ∀ A ∈ V (x ∈ ◻ A ⇒ y ∈ A), {\ displaystyle \ langle x / {\ sim}, y / {\ sim } \ rangle \ in S \ iff \ forall A \ in V \, (x \ in \ Box A \ Rightarrow y \ in A),}

{\ displaystyle \ langle x / {\ sim}, y / {\ sim} \ rangle \ in S \ iff \ forall A \ in V \, (x \ in \ Box A \ Rightarrow y \ in A),}

A / ∼ ∈ W ⟺ A ∈ V. {\ displaystyle A / {\ sim} \ in W \ iff A \ in V.}

{\ displaystyle A / {\ sim} \ in W \ iff A \ in V.}

Полнота

В отличие от фреймов Крипке, каждая нормальная модальная логика L завершена по отношению к классу общих фреймов. Это является следствием того факта, что L полна относительно класса моделей Крипке $⟨F, R, ⊩⟩ {\ displaystyle \ langle F, R, {\ Vdash} \ rangle}$ ${\ displaystyle \ langle F, R, {\ Vdash} \ rangle}$ : поскольку L замкнут при подстановке, общий фрейм, индуцированный $⟨F, R, ⊩⟩ {\ displaystyle \ langle F, R, {\ Vdash} \ rangle}$ ${\ displaystyle \ langle F, R, {\ Vdash} \ rangle}$ , является L- Рамка. Более того, каждая логика L полна относительно единственного описательного фрейма. Действительно, L полна по отношению к своей канонической модели, а общая шкала, индуцированная канонической моделью (называемая канонической системой отсчета L), является описательной.

Двойственность Йонссона – Тарского

Лестница Ригера – Нисимуры: 1-универсальная интуиционистская шкала Крипке.

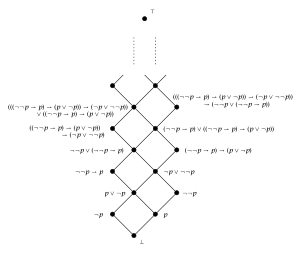
Ее двойственная алгебра Гейтинга, решетка Ригера – Нисимуры. Это бесплатная алгебра Гейтинга над генератором 1.

Общие системы отсчета тесно связаны с модальными алгебрами. Пусть $F = ⟨F, R, V⟩ {\ displaystyle \ mathbf {F} = \ langle F, R, V \ rangle}$ ${\ mathbf F} = \ langle F, R, V \ rangle$ будет общим фреймом. Множество V замкнуто относительно булевых операций, поэтому оно является подалгеброй набора степеней булевой алгебры $⟨P (F), ∩, ∪, -⟩ {\ displaystyle \ langle {\ mathcal {P}} (F), \ cap, \ cup, - \ rangle}$ ${\ displaystyle \ langle {\ mathcal {P}} (F), \ cap, \ cup, - \ rangle}$ . Он также выполняет дополнительную унарную операцию, $◻ {\ displaystyle \ Box}$ $\ Box$ . Комбинированная структура $⟨V, ∩, ∪, -, ◻⟩ {\ displaystyle \ langle V, \ cap, \ cup, -, \ Box \ rangle}$ ${\ displaystyle \ langle V, \ cap, \ cup, -, \ Box \ rangle}$ представляет собой модальную алгебру, которая называется дуальной алгеброй к F и обозначается $F + {\ displaystyle \ mathbf {F} ^ {+}}$ ${\ displaystyle \ mathbf {F} ^ {+}}$ .

В противоположном направлении это можно построить двойной фрейм $A + = ⟨F, R, V⟩ {\ displaystyle \ mathbf {A} _ {+} = \ langle F, R, V \ rangle}$ ${\ displaystyle \ mathbf {A} _ {+} = \ langle F, R, V \ rangle}$ в любую модальную алгебру $A = ⟨A, ∧, ∨, -, ◻⟩ {\ displaystyle \ mathbf {A} = \ langle A, \ wedge, \ vee, -, \ Box \ rangle}$ ${\ displaystyle \ mathbf {A} = \ langle A, \ wedge, \ vee, -, \ Box \ rangle}$ . Булева алгебра $⟨A, ∧, ∨, -⟩ {\ displaystyle \ langle A, \ wedge, \ vee, - \ rangle}$ ${\ displaystyle \ langle A, \ wedge, \ vee, - \ rangle}$ имеет каменное пространство, базовый набор F - это набор всех ультрафильтров из A . Множество V допустимых оценок в $A + {\ displaystyle \ mathbf {A} _ {+}}$ ${\ displaystyle \ mathbf {A} _ {+} }$ состоит из clopen подмножеств F и отношения доступности R определяется формулой

Икс R Y ⟺ ⟺ a ∈ A (◻ a ∈ x ⇒ a ∈ y) {\ displaystyle x \, R \, y \ iff \ forall a \ in A \, (\ Box a \ in x \ Rightarrow a \ in y)}

{\ displaystyle x \, R \, y \ iff \ forall a \ in A \, (\ Box a \ in x \ Rightarrow a \ in y)}

для всех ультрафильтров x и y.

Фрейм и его двойник проверяют одни и те же формулы, поэтому общая семантика фрейма и алгебраическая семантика в некотором смысле эквивалентны. Двойное двойственное число $(A +) + {\ displaystyle (\ mathbf {A} _ {+}) ^ {+}}$ ${\ displaystyle (\ mathbf {A} _ {+}) ^ {+}}$ любой модальной алгебры изоморфно $A {\ displaystyle \ mathbf {A}}$ $\ mathbf {A}$ сам. В общем случае это неверно для двойных двойников фреймов, поскольку двойник каждой алгебры описательный. Фактически, фрейм $F {\ displaystyle \ mathbf {F}}$ $\ mathbf {F }$ является описательным тогда и только тогда, когда он изоморфен своему двойному двойному $(F +) + {\ displaystyle (\ mathbf {F} ^ {+}) _ {+}}$ ${\ displaystyle (\ mathbf {F} ^ {+}) _ {+}}$ .

Также возможно определить двойники p-морфизмов, с одной стороны, и гомоморфизмы модальной алгебры, с другой. Таким образом, операторы $(⋅) + {\ displaystyle (\ cdot) ^ {+}}$ $(\ cdot) ^ {+}$ и $(⋅) + {\ displaystyle (\ cdot) _ {+}}$ ${\ displaystyle (\ cdot) _ {+}}$ становится парой контравариантных функторов между категорией общих шкал и категорией модальных алгебр. Эти функторы обеспечивают двойственность (названную двойственностью Йонссона-Тарского после Бьярни Йонссона и Альфреда Тарски ) между категориями описательных фреймов, и модальные алгебры. Это частный случай более общей двойственности между комплексными алгебрами и полями множеств в реляционных структурах.

Интуиционистские фреймы

Семантика фреймов для интуиционистской и промежуточной логики может развиваться параллельно с семантикой. для модальной логики. интуиционистский общий фрейм - это тройка $⟨F, ≤, V⟩ {\ displaystyle \ langle F, \ leq, V \ rangle}$ ${\ displaystyle \ langle F, \ leq, V \ rangle }$ , где $≤ { \ displaystyle \ leq}$ $\ leq$ - это частичный порядок на F, а V - это набор верхних подмножеств (конусов) F, который содержит пустой набор, и закрывается при

пересечении и объединении,
операция $A → B = ◻ (- A ∪ B) {\ displaystyle A \ to B = \ Box (-A \ cup B)}$ ${\ displaystyle A \ to B = \ Box (-A \ чашка B)}$ .

Затем вводятся валидность и другие концепции, аналогично модальным фреймам, с некоторыми изменениями, необходимыми для учета более слабых свойств замыкания множества допустимых оценок. В частности, интуиционистский фрейм $F = ⟨F, ≤, V⟩ {\ displaystyle \ mathbf {F} = \ langle F, \ leq, V \ rangle}$ ${\ mathbf F} = \ langle F, \ leq, V \ rangle$ называется

плотным, если $∀ A ∈ V (x ∈ A ⇔ y ∈ A) {\ displaystyle \ forall A \ in V \, (x \ in A \ Leftrightarrow y \ in A)}$ ${\ displaystyle \ forall A \ in V \, (x \ in A \ Leftrightarrow y \ in A)}$ подразумевает $x ≤ y {\ displaystyle x \ leq y}$ $x \ leq y$ ,
compact, если каждое подмножество $V ∪ {F - A; A ∈ V} {\ displaystyle V \ cup \ {FA; \, A \ in V \}}$ ${\ Displaystyle V \ чашка \ {FA; \, A \ in V \}}$ со свойством конечного пересечения имеет непустое пересечение.

Тесные интуиционистские рамки автоматически дифференцируются, следовательно, уточнены.

Двойник интуиционистской рамки $F = ⟨F, ≤, V⟩ {\ displaystyle \ mathbf {F} = \ langle F, \ leq, V \ rangle}$ ${\ mathbf F} = \ langle F, \ leq, V \ rangle$ это алгебра Гейтинга $F + = ⟨V, ∩, ∪, →, ∅⟩ {\ displaystyle \ mathbf {F} ^ {+} = \ langle V, \ cap, \ cup, \ to, \ emptyset \ rangle}$ ${\ displaystyle \ mathbf {F} ^ {+} = \ langle V, \ cap, \ чашка, \ to, \ emptyset \ rangle}$ . Двойственная алгебра Гейтинга $A = ⟨A, ∧, ∨, →, 0⟩ {\ displaystyle \ mathbf {A} = \ langle A, \ wedge, \ vee, \ to, 0 \ rangle}$ ${\ displaystyle \ mathbf {A} = \ langle A, \ wedge, \ vee, \ to, 0 \ rangle}$ - интуиционистский фрейм. $A + = ⟨F, ≤, V⟩ {\ displaystyle \ mathbf {A} _ {+} = \ langle F, \ leq, V \ rangle}$ ${\ displaystyle \ mathbf {A} _ {+} = \ langle F, \ leq, V \ rangle}$ , где F - набор всех простых фильтров из A, порядок $≤ {\ displaystyle \ leq}$ $\ leq$ - включение, а V состоит из всех подмножеств F вида

{x ∈ F; a ∈ x}, {\ displaystyle \ {x \ in F; \, a \ in x \},}

{\ displaystyle \ {x \ in F; \, a \ in x \},}

где $a ∈ A {\ displaystyle a \ in A}$ $a \ in A$ . Как и в модальном случае, $(⋅) + {\ displaystyle (\ cdot) ^ {+}}$ $(\ cdot) ^ {+}$ и $(⋅) + {\ displaystyle (\ cdot) _ {+} }$ ${\ displaystyle (\ cdot) _ {+}}$ - пара контравариантных функторов, которые делают категорию алгебр Гейтинга двойственно эквивалентной категории описательных интуиционистских фреймов.

Можно построить интуиционистские общие фреймы из транзитивных рефлексивных модальных фреймов и наоборот, см. модальный компаньон.

Ссылки

Александр Чагров и Михаил Захарьящев, Модальная логика, т. 35 из Oxford Logic Guides, Oxford University Press, 1997.
Патрик Блэкберн, Маартен де Рийке и Иде Венема, Modal Logic, vol. 53 Кембриджских трактатов по теоретической информатике, Cambridge University Press, 2001.