ЭрлангФункция плотности вероятности  |
Кумулятивная функция распределения 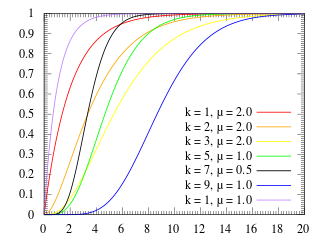 |
| Параметры |  shape. shape.  скорость. alt.: скорость. alt.:  scale scale |
|---|
| Support |  |
|---|
| PDF |  |
|---|
| CDF |  |
|---|
| Среднее |  |
|---|
| Медиана | Нет простой закрытой формы |
|---|
| Режим |  |
|---|
| Дисперсия |  |
|---|
| Асимметрия |  |
|---|
| Пример. эксцесс |  |
|---|
| Энтропия | ![{\ displaystyle (1-k) \ psi (k) + \ ln \ left [{\ frac {\ Gamma (k)} {\ lambda}} \ right] + k}](https://wikimedia.org/api/rest_v1/media/math/render/svg/274f6ef68b61a8f859d3c49d5ba4a0fec6590ed8) |
|---|
| MGF |  для для  |
|---|
| CF |  |
|---|
Распределение Эрланга - это двухпараметрическое семейство непрерывных распределения вероятностей с поддержкой  . Двумя параметрами являются:
. Двумя параметрами являются:
- положительное целое число
 «форма» и
«форма» и - положительное вещественное число
 «скорость». Вместо этого иногда используется "масштаб",
«скорость». Вместо этого иногда используется "масштаб",  , обратная скорости.
, обратная скорости.
Распределение Эрланга с параметром формы  упрощается до экспоненциального распределения. Это частный случай гамма-распределения. Это распределение суммы
упрощается до экспоненциального распределения. Это частный случай гамма-распределения. Это распределение суммы  независимых экспоненциальных переменных со средним значением
независимых экспоненциальных переменных со средним значением  каждый.
каждый.
Распределение Эрланга было разработано А. К. Эрланг для проверки количества телефонных звонков, которые могут быть сделаны одновременно операторам коммутационных станций. Эта работа по организации телефонного трафика была расширена с учетом времени ожидания в системах очередей в целом. Распределение также используется в области случайных процессов.
Содержание
- 1 Характеристика
- 1.1 Функция плотности вероятности
- 1.2 Кумулятивная функция распределения (CDF)
- 1.3 Медиана
- 2 Создание Случайные переменные, распределенные по Эрлангу
- 3 Приложения
- 3.1 Время ожидания
- 3.2 Другие приложения
- 4 Свойства
- 5 Связанные распределения
- 6 См. Также
- 7 Примечания
- 8 Ссылки
- 9 Внешние ссылки
Характеристика
Функция плотности вероятности
функция плотности вероятности распределения Эрланга равна

Параметр k называется параметром формы, а параметр  называется параметром скорости.
называется параметром скорости.
Альтернативная, но эквивалентная параметризация использует параметр масштаба  , который является обратной величиной параметра скорости (т. Е.
, который является обратной величиной параметра скорости (т. Е.  ):
):

Если параметр масштаба  равно 2, распределение упрощается до распределения хи-квадрат с 2k степенями свободы. Следовательно, его можно рассматривать как обобщенное распределение хи-квадрат для четного числа степеней свободы.
равно 2, распределение упрощается до распределения хи-квадрат с 2k степенями свободы. Следовательно, его можно рассматривать как обобщенное распределение хи-квадрат для четного числа степеней свободы.
Кумулятивная функция распределения (CDF)
Кумулятивная функция распределения распределения Эрланга:

где  - нижняя неполная гамма-функция, а
- нижняя неполная гамма-функция, а  - нижняя регуляризованная гамма-функция. CDF также может быть выражен как
- нижняя регуляризованная гамма-функция. CDF также может быть выражен как

Медиана
Известно асимптотическое разложение для медианы распределения Эрланга, для которого можно вычислить коэффициенты и известны границы. Приближение:  т.е. ниже среднего
т.е. ниже среднего 
Генерация случайных величин, распределенных по Эрлангу
Случайные величины, распределенные по Эрлангу, можно сгенерировать из равномерно распределенных случайных чисел (![U \ in (0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/123458e6968de4b251de863aa008e7dd442c51f3) ) по следующей формуле:
) по следующей формуле:

Приложения
Время ожидания
События, которые происходят независимо с некоторой средней скоростью, моделируются с помощью пуассоновского процесса. Время ожидания между k появлением события распределяется по Эрлангу (связанный вопрос количества событий за заданный промежуток времени описывается распределением Пуассона.)
Распределение Эрланга, которое измеряет время между входящими вызовами, может использоваться в сочетании с ожидаемая продолжительность входящих вызовов для получения информации о загруженности трафика, измеряемой в эрлангах. Это можно использовать для определения вероятности потери или задержки пакета в соответствии с различными предположениями о том, прерываются ли заблокированные вызовы (формула Эрланга B) или ставятся в очередь до обслуживания (формула Эрланга C). Формулы Erlang-B и C до сих пор ежедневно используются для моделирования трафика для таких приложений, как проектирование центров обработки вызовов.
других приложений
Распределение по возрасту рака заболеваемости часто следует распределению Эрланга, тогда как параметры формы и масштаба предсказывают, соответственно, количество событий водителя и временной интервал между их. В более общем плане распределение Эрланга было предложено как хорошее приближение распределения времени цикла ячеек в результате многоступенчатых моделей.
Оно также использовалось в экономике бизнеса для описания времени между покупками.
Свойства
- Если
 , то
, то  с
с 
- Если
 и
и  затем
затем 
Связанные распределения
- Распределение Эрланга - это распределение суммы k независимых и одинаково распределенные случайные величины, каждая из которых имеет экспоненциальное распределение. Долгосрочная скорость, с которой происходят события, является обратной величиной ожидания
 , то есть
, то есть  Частота (возрастных событий) распределения Эрланга для
Частота (возрастных событий) распределения Эрланга для  монотонный в
монотонный в  увеличивается от 0 при
увеличивается от 0 при  до
до  as
as  стремится к бесконечности.
стремится к бесконечности. - То есть: если
 , затем
, затем 
- Из-за факториальной функции в знаменателе PDF и CDF, распределение Эрланга определяется только тогда, когда параметр k является положительным целым числом. Фактически, это распределение иногда называют Эрланг-k распределение (например, распределение Эрланга-2 является распределением Эрланга с
 ). Гамма-распределение обобщает распределение Эрланга, позволяя k быть любым положительным вещественным числом, используя гамма-функцию вместо факториальной функции.
). Гамма-распределение обобщает распределение Эрланга, позволяя k быть любым положительным вещественным числом, используя гамма-функцию вместо факториальной функции. - То есть: если k является целым числом и
 , тогда
, тогда 
- Если
 и
и  , затем
, затем 
- Распределение Эрланга является частным случаем распределения Пирсона типа III
- Распределение Эрланга связано с распределением хи-квадрат. Если
 , то
, то 
- Распределение Эрланга связано с распределением Пуассона посредством процесса Пуассона : Если
 такой, что
такой, что  , затем
, затем  и
и  Если взять различия в
Если взять различия в  , получим распределение Пуассона.
, получим распределение Пуассона.
См. Также
Примечания
- ^Чой, К.П. (1994). «О медианах гамма-распределений и уравнении Рамануджана». Proceedings of the American Mathematical Society. 121 : 245–251. doi : 10.1090 / S0002-9939-1994-1195477-8. JSTOR 2160389.
- ^Adell, JA; Jodrá, P. (2007). «Об уравнении Рамануджана соедините с медианой гамма-распределения ". Труды Американского математического общества. 360 (7): 3631. doi : 10.1090 / S0002-9947-07-04411-X.
- ^Йодра, П. (2012). «Вычисление асимптотического разложения медианы распределения Эрланга». Математическое моделирование и анализ. 17 (2): 281–292. doi : 10.3846 / 13926292.2012.664571.
- ^Баннехека, BMSG; Эканаяке, GEMUPD (2009). «Новая точечная оценка медианы гамма-распределения». Viyodaya J Science. 14 : 95–103.
- ^Resa. «Статистические распределения - Распределение Эрланга - Генератор случайных чисел». www.xycoon.com. Дата обращения 4 апреля 2018 г.
- ^Беликов Алексей В. (22 сентября 2017 г.). «Количество ключевых канцерогенных событий можно предсказать по заболеваемости раком». Научные отчеты. 7 (1). DOI : 10.1038 / s41598-017-12448-7. PMC 5610194. PMID 28939880.
- ^Йейтс, Кристиан А. (21 апреля 2017 г.). «Многоступенчатое представление клеточной пролиферации как марковского процесса». Вестник математической биологии. 79 (1): 2905–2928. doi : 10.1007 / s11538-017-0356-4.
- ^Гаваньин, Энрико (14 октября 018 г.). «Скорость вторжения моделей миграции клеток с реалистичным распределением времени клеточного цикла». Журнал теоретической биологии. 79 (1): 91–99. arXiv : 1806.03140. doi : 10.1016 / j.jtbi.2018.09.010.
- ^C. Чатфилд и Г.Дж. Гудхардт: «Модель потребительских закупок с учетом времени межпокупок в Эрланге»; Журнал Американской статистической ассоциации, декабрь 1973 г., том 68, стр. 828-835
- ^Кокс, Д. (1967) Теория обновления, стр. 20, Метуэн.
Ссылки
- Ян Ангус «Введение в Erlang B и Erlang C», Telemanagement # 187 (документ PDF - содержит термины и формулы, а также краткую биографию)
- Стюарт Харрис «Вычисления Erlang против моделирования»
Внешние ссылки


 shape.
shape.  скорость. alt.:
скорость. alt.:  scale
scale 







![{\ displaystyle (1-k) \ psi (k) + \ ln \ left [{\ frac {\ Gamma (k)} {\ lambda}} \ right] + k}](https://wikimedia.org/api/rest_v1/media/math/render/svg/274f6ef68b61a8f859d3c49d5ba4a0fec6590ed8)
 для
для 


 «форма» и
«форма» и «скорость». Вместо этого иногда используется "масштаб",
«скорость». Вместо этого иногда используется "масштаб",  , обратная скорости.
, обратная скорости.













![U \ in (0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/123458e6968de4b251de863aa008e7dd442c51f3)

 , то
, то  с
с 
 и
и  затем
затем 
 , то есть
, то есть  Частота (возрастных событий) распределения Эрланга для
Частота (возрастных событий) распределения Эрланга для  монотонный в
монотонный в  увеличивается от 0 при
увеличивается от 0 при  до
до  as
as  стремится к бесконечности.
стремится к бесконечности.  , затем
, затем 
 ). Гамма-распределение обобщает распределение Эрланга, позволяя k быть любым положительным вещественным числом, используя гамма-функцию вместо факториальной функции.
). Гамма-распределение обобщает распределение Эрланга, позволяя k быть любым положительным вещественным числом, используя гамма-функцию вместо факториальной функции.  , тогда
, тогда 
 и
и  , затем
, затем 
 , то
, то 
 такой, что
такой, что  , затем
, затем  и
и  Если взять различия в
Если взять различия в  , получим распределение Пуассона.
, получим распределение Пуассона.