Уравнение Бете – Солпитера

Уравнение Бете – Солпитера (названо в честь Ганса Бете и Эдвин Солпетер ) описывает связанные состояния двухчастичной квантовой теоретико-полевой системы в релятивистски ковариантном формализме. Фактически это уравнение было впервые опубликовано в 1950 году в конце статьи Йохиро Намбу, но без вывода.

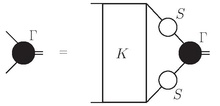Графическое представление уравнения Бете – Солпитера, показывающее его рекурсивное определение

Из-за Благодаря своей общности и применению во многих разделах теоретической физики уравнение Бете – Солпитера проявляется во многих различных формах. Одна форма, которая довольно часто используется в физике высоких энергий, - это

$\Gamma \; (P,\; p)\; =\; \int \; d\; 4\; k\; (2\; \pi )\; 4\; K\; (P,\; p,\; k)\; S\; (k\; -\; П\; 2)\; \Gamma \; (п,\; к)\; S\; (к\; +\; п\; 2)\; \{\backslash \; displaystyle\; \backslash \; Gamma\; (P,\; p)\; =\; \backslash \; int\; \backslash !\; \{\backslash \; Frac\; \{d\; ^\; \{4\}\; k\}\; \{(2\; \backslash \; pi)\; ^\; \{\; 4\}\}\}\; \backslash ;\; K\; (P,\; p,\; k)\; \backslash ,\; S\; (k\; -\; \{\backslash \; tfrac\; \{P\}\; \{2\}\})\; \backslash ,\; \backslash \; Gamma\; (P,\; k)\; \backslash ,\; S\; (k\; +\; \{\backslash \; tfrac\; \{P\; \}\; \{2\}\})\}$

где Γ - амплитуда Бете – Солпитера, K - взаимодействие и S - пропагаторы двух участвующих частиц.

В квантовой теории связанные состояния - это объекты, которые существуют в течение бесконечного времени (иначе их называют резонансами ), поэтому составляющие взаимодействуют бесконечно много раз. Суммируя бесконечно много раз все возможные взаимодействия, которые могут происходить между двумя составляющими, уравнение Бете – Солпитера является инструментом для вычисления свойств связанных состояний. Ее решение - амплитуда Бете – Солпитера - описывает рассматриваемое связанное состояние.

Поскольку он может быть получен путем идентификации связанных состояний с полюсами в S-матрице, его можно связать с квантово-теоретическим описанием процессов рассеяния и функциями Грина.

Уравнение Бете – Солпитера - это общий инструмент квантовой теории поля, поэтому его приложения можно найти в любой квантовой теории поля. Некоторыми примерами являются позитроний (связанное состояние пары электрон - позитрон ), экситоны (связанное состояние электрон - дырка пара) и мезоны (как кварк -антикварковое связанное состояние).

Даже для простых систем, таких как позитрония уравнение нельзя решить точно, хотя в принципе его можно точно сформулировать. Классификация состояний может быть достигнута без необходимости точного решения. Если одна из частиц значительно массивнее, чем другая, проблема значительно упрощается, поскольку решается уравнение Дирака для более легкой частицы под внешним потенциалом более тяжелой частицы.

• 1 Деривация
• 2 Радужно-лестничное приближение
• 3 Нормализация
• 4 См. Также
• 5 Ссылки
• 6 Библиография
• 7 Внешние ссылки

Отправной точкой для вывода уравнения Бете – Солпитера является двухчастичное (или четырехточечное) уравнение Дайсона

$G\; =\; S\; 1\; S\; 2\; +\; S\; 1\; S\; 2\; K\; 12\; G\; \{\backslash \; displaystyle\; G\; =\; S\_\; \{1\}\; \backslash ,\; S\_\; \{2\}\; +\; S\_\; \{1\}\; \backslash ,\; S\_\; \{2\}\; \backslash ,\; K\_\; \{12\}\; \backslash ,\; G\}$

в импульсном пространстве, где "G" - двухчастичная Функция Грина $⟨\Omega \; |\; \varphi \; 1\; \varphi \; 2\; \varphi \; 3\; \varphi \; 4\; |\; Ом⟩\; \{\backslash \; Displaystyle\; \backslash \; langle\; \backslash \; Omega\; |\; \backslash \; phi\; \_\; \{1\}\; \backslash ,\; \backslash \; phi\; \_\; \{2\}\; \backslash ,\; \backslash \; phi\; \_\; \{3\}\; \backslash ,\; \backslash \; phi\; \_\; \{4\}\; |\; \backslash \; Omega\; \backslash \; rangle\}$, «S» - это свободные пропагаторы, а «K» - ядро ​​взаимодействия, которое содержит все возможные взаимодействия между двумя частицами. Решающим шагом теперь является предположение, что связанные состояния появляются как полюсы в функции Грина. Предполагается, что две частицы объединяются и образуют связанное состояние с массой "M", это связанное состояние распространяется свободно, а затем связанное состояние снова распадается на две составляющие. Поэтому вводится волновая функция Бете – Солпитера $\Psi \; =\; ⟨\Omega \; |\; \varphi \; 1\; \varphi \; 2\; |\; \psi ⟩\; \{\backslash \; displaystyle\; \backslash \; Psi\; =\; \backslash \; langle\; \backslash \; Omega\; |\; \backslash \; phi\; \_\; \{1\}\; \backslash ,\; \backslash \; phi\; \_\; \{2\}\; |\; \backslash \; psi\; \backslash \; rangle\}$, что представляет собой амплитуду перехода двух составляющих $\varphi \; i\; \{\backslash \; displaystyle\; \backslash \; phi\; \_\; \{i\}\}$в связанное состояние $\psi \; \{\backslash \; displaystyle\; \backslash \; psi\}$, а затем делает анзац для функции Грина в окрестность полюса как

$G\; \approx \; \Psi \; \Psi \; ¯\; P\; 2\; -\; M\; 2,\; \{\backslash \; displaystyle\; G\; \backslash \; приблизительно\; \{\backslash \; frac\; \{\backslash \; Psi\; \backslash ;\; \{\backslash \; bar\; \{\backslash \; Psi\}\}\}\; \{P\; ^\; \{2\}\; -\; M\; ^\; \{2\}\}\},\}$

где P - полный импульс системы. Видно, что если для этого импульса выполняется уравнение $P\; 2\; =\; M\; 2\; \{\backslash \; displaystyle\; P\; ^\; \{2\}\; =\; M\; ^\; \{2\}\}$, то какова именно энергия Эйнштейна отношение -импульс (с Четыре-импульсом $P\; \mu \; =\; (E\; /\; c,\; p\; \to )\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; mu\}\; =\; \backslash \; left\; (E\; /\; c,\; \{\backslash \; vec\; \{p\}\}\; \backslash \; right)\}$и $P\; 2\; =\; P\; \mu \; P\; \mu \; \{\backslash \; displaystyle\; P\; ^\; \{2\}\; =\; P\; \_\; \{\backslash \; mu\}\; \backslash ,\; P\; ^\; \{\backslash \; mu\}\}$) четырехточечная функция Грина содержит полюс. Если подставить этот анзац в приведенное выше уравнение Дайсона и установить полный импульс «P» таким образом, чтобы соблюдалось соотношение энергии-импульса, по обе стороны от члена появится полюс.

$\Psi \; \Psi \; ¯\; п\; 2\; -\; M\; 2\; знак\; равно\; S\; 1\; S\; 2\; +\; S\; 1\; S\; 2\; K\; 12\; \Psi \; \Psi \; ¯\; п\; 2\; -\; M\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; Psi\; \backslash ;\; \{\backslash \; bar\; \{\backslash \; Psi\}\}\; \}\; \{P\; ^\; \{2\}\; -M\; ^\; \{2\}\}\}\; =\; S\_\; \{1\}\; \backslash ,\; S\_\; \{2\}\; +\; S\_\; \{1\}\; \backslash ,\; S\_\; \{2\}\; \backslash ,\; K\_\; \{12\}\; \{\backslash \; frac\; \{\backslash \; Psi\; \backslash \; ;\; \{\backslash \; bar\; \{\backslash \; Psi\}\}\}\; \{P\; ^\; \{2\}\; -M\; ^\; \{2\}\}\}\}$

Сравнение остатков дает

$\Psi \; =\; S\; 1\; S\; 2\; K\; 12\; \Psi ,\; \{\backslash \; displaystyle\; \backslash \; Psi\; =\; S\_\; \{1\}\; \backslash ,\; S\_\; \{2\}\; \backslash ,\; K\_\; \{12\}\; \backslash \; Psi,\; \backslash ,\}$

Это уже уравнение Бете – Солпитера, записанное в терминах волновых функций Бете – Солпитера. Чтобы получить вышеуказанную форму, вводятся амплитуды Бете – Солпитера «Γ»

$\Psi \; =\; S\; 1\; S\; 2\; \Gamma \; \{\backslash \; displaystyle\; \backslash \; Psi\; =\; S\_\; \{1\}\; \backslash ,\; S\_\; \{2\}\; \backslash ,\; \backslash \; Gamma\}$

и окончательно получает

$\Gamma \; =\; K\; 12\; S\; 1\; S\; 2\; \Gamma \; \{\backslash \; displaystyle\; \backslash \; Gamma\; =\; K\_\; \{12\}\; \backslash ,\; S\_\; \{1\}\; \backslash ,\; S\_\; \{2\}\; \backslash ,\; \backslash \; Gamma\}$

, который записан выше, с явной зависимостью от импульса.

Графическое представление уравнения Бете – Солпитера в лестничном приближении

В принципе ядро ​​взаимодействия K содержит все возможные двухчастичные неприводимые взаимодействия, которые могут происходить между ними. составляющие. Таким образом, в практических расчетах необходимо смоделировать это и выбрать только подмножество взаимодействий. Как и в квантовых теориях поля, взаимодействие описывается через обмен частицами (например, фотонами в квантовой электродинамике или глюонами в квантовая хромодинамика ), самое простое взаимодействие - это обмен только одной из этих сил-частиц.

Поскольку уравнение Бете – Солпитера суммирует взаимодействие бесконечно много раз, результирующий граф Фейнмана имеет форму лестницы (или радуги).

В то время как в квантовой электродинамике лестничное приближение вызывало проблемы с перекрестной симметрией и калибровочной инвариантностью, и, следовательно, необходимо было включить перекрестные лестничные члены, в квантовой хромодинамике это приближение используется феноменологически довольно сложно вычислить массы адронов, поскольку он учитывает нарушение киральной симметрии и, следовательно, является важной частью генерации этих масс.

Как и для любого однородного уравнения, решение уравнения Бете – Солпитера определяется только с точностью до числового коэффициента. Этот коэффициент должен быть указан определенным условием нормировки. Для амплитуд Бете – Солпитера это обычно делается путем требования сохранения вероятности (аналогично нормировке квантово-механической волновой функции ), что соответствует уравнению

$2\; P\; \mu \; =\; \Gamma \; ¯\; (\partial \; \partial \; П\; \mu \; (S\; 1\; \otimes \; S\; 2)\; -\; S\; 1\; S\; 2\; (\partial \; \partial \; P\; \mu \; K)\; S\; 1\; S\; 2)\; \Gamma \; \{\backslash \; displaystyle\; 2P\; \_\; \{\backslash \; mu\}\; =\; \{\backslash \; bar\; \{\backslash \; Gamma\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; P\; \_\; \{\backslash \; mu\}\}\}\; \backslash \; left\; (S\_\; \{1\}\; \backslash \; otimes\; S\_\; \{2\}\; \backslash \; right)\; -S\_\; \{1\}\; \backslash ,\; S\_\; \{2\}\; \backslash ,\; \backslash \; left\; (\{\backslash \; frac\; \{\; \backslash \; partial\}\; \{\backslash \; partial\; P\; \_\; \{\backslash \; mu\}\}\}\; \backslash ,\; K\; \backslash \; right)\; \backslash ,\; S\_\; \{1\}\; \backslash ,\; S\_\; \{2\}\; \backslash \; right)\; \backslash \; Gamma\}$

Нормализация к тензору заряда и энергии-импульса связанное состояние приводит к тому же уравнению. В лестничном приближении ядро ​​взаимодействия не зависит от полного импульса амплитуды Бете – Солпитера, поэтому в этом случае второй член условия нормировки обращается в нуль.

• ABINIT - плоская волна
• Поправка Араки – Сухера
• Уравнение Брейта
• Уравнение Липпмана – Швингера
• Уравнение Швингера – Дайсона
• Двухчастичное Уравнения Дирака
• Код ЯМБО - плоская волна

Многие современные учебники по квантовой теории поля и несколько статей содержат педагогические объяснения контекста уравнения Бете – Солпитера и использует. См.:

• W. Грейнер, Дж. Рейнхардт (2003). Квантовая электродинамика (3-е изд.). Спрингер. ISBN 978-3-540-44029-1.
• Z.K. Силагадзе (1998). «Модель Вика – Каткоски: Введение». arXiv : hep-ph / 9803307.

Тем не менее, хорошее введение дает обзорная статья Наканиши

• Н. Наканиши (1969). «Общий обзор теории уравнения Бете – Солпитера». Приложение к прогрессу теоретической физики. 43: 1–81. Bibcode : 1969PThPS..43.... 1N. doi : 10.1143 / PTPS.43.1.

Исторические аспекты см. В

• E.E. Солпитер (2008). «Уравнение Бете – Солпитера (истоки)». Scholarpedia. 3(11): 7483. arXiv : 0811.1050. Bibcode : 2008SchpJ... 3.7483S. doi : 10.4249 / scholarpedia.7483.

• BerkeleyGW - метод плоских волн псевдопотенциала
• ExC - плоская волна
• Fiesta - Гауссовский полностью электронный метод