Спираль Эйлера

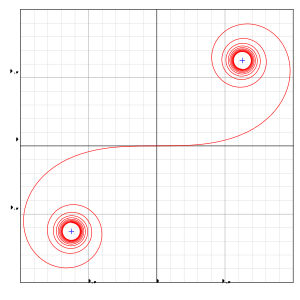
Двусторонняя спираль Эйлера. Кривая продолжает сходиться к отмеченным точкам, поскольку t стремится к положительной или отрицательной бесконечности.

Спираль Эйлера - это кривая, кривизна которой изменяется линейно с длиной кривой ( кривизна круговой кривой равна обратной величине радиуса). Спирали Эйлера также обычно называют спиралями, клотоидами или спиралями Корну .

Спирали Эйлера имеют приложения для дифракционных вычислений. Они также широко используются в качестве переходных кривых в железнодорожном строительстве / дорожном строительстве для соединения и перехода геометрии между касательной и круговой кривой. Аналогичное применение также можно найти в фотонных интегральных схемах. Принцип линейного изменения кривизны переходной кривой между касательной и круговой кривой определяет геометрию спирали Эйлера:

• Ее кривизна начинается с нуля на прямом участке (касательной) и линейно увеличивается с увеличением длины кривой..
• Там, где спираль Эйлера встречается с круговой кривой, ее кривизна становится равной кривизне последней.

• 1 Приложения
  • 1.1 Кривая перехода трека
  • 1.2 Оптика
  • 1.3 Интегрированная оптика
  • 1.4 Автогонки
  • 1.5 Типографика и цифровая векторная графика
  • 1.6 Проекция карты
  • 1.7 Формы усов
• 2 Формулировка
  • 2.1 Символы
  • 2.2 Расширение интеграла Френеля
  • 2.3 Нормализация и заключение
    • 2.3.1 Иллюстрация
  • 2.4 Другие свойства нормализованных спиралей Эйлера
• 3 Код для создания спирали Эйлера
• 4 См. Также
• 5 Ссылки
• 6 Дополнительная литература
• 7 Внешние ссылки

Кривая перехода трека

Анимация, изображающая эволюцию Cornu sp Параллельно с тангенциальным кругом с таким же радиусом кривизны, что и на его вершине, также известный как соприкасающийся круг.

Чтобы двигаться по круговой траектории, объект должен подвергаться центростремительному ускорению (например: луна вращается вокруг земли под действием силы тяжести; автомобиль поворачивает свои передние колеса внутрь, чтобы создать центростремительную силу). Если транспортное средство, движущееся по прямой дороге, внезапно перейдет на тангенциальную круговую траекторию, это потребует внезапного переключения центростремительного ускорения в точке касания с нуля на требуемое значение; Этого было бы трудно достичь (представьте себе водителя, который мгновенно переводит рулевое колесо из прямого положения в положение поворота, и машина фактически делает это), оказывая механическую нагрузку на детали автомобиля и вызывая сильный дискомфорт (из-за бокового рывок ).

На ранних железных дорогах это мгновенное приложение поперечной силы не было проблемой, поскольку использовались низкие скорости и повороты с широким радиусом (поперечные силы на пассажиров и поперечное колебание были небольшими и допустимыми). По мере того как скорость рельсовых транспортных средств с годами увеличивалась, стало очевидно, что необходим сервитут, так что центростремительное ускорение увеличивается линейно с пройденным расстоянием. Учитывая выражение центростремительного ускорения V² / R, очевидным решением является создание кривой сервитута, кривизна которой, 1 / R, увеличивается линейно с пройденным расстоянием. Эта геометрия представляет собой спираль Эйлера.

Не зная о решении геометрии Леонарда Эйлера, Ранкин процитировал кубическую кривую (полиномиальная кривая степени 3), которая представляет собой приближение спирали Эйлера для малых угловых изменений так же, как парабола является приближением круговой кривой.

Мари Альфред Корню (а позже и некоторые инженеры-строители) также независимо решила исчисление спирали Эйлера. Спирали Эйлера теперь широко используются в строительстве железных дорог и шоссе для обеспечения перехода или облегчения между касательной и горизонтальной круговой кривой.

Оптика

Спираль Корню может использоваться для описания дифракционной картины. Рассмотрим плоскую волну с амплитудой фазора $E\; oe\; -\; jkz\; \{\backslash \; displaystyle\; E\_\; \{o\}\; e\; ^\; \{-\; jkz\}\}$, которая дифрагирует на «острие лезвия» высотой $h\; \{\; \backslash \; displaystyle\; h\}$выше $x\; =\; 0\; \{\backslash \; displaystyle\; x\; =\; 0\}$на $z\; =\; 0\; \{\backslash \; displaystyle\; z\; =\; 0\}$самолет. Тогда поле дифрагированной волны можно выразить как

$E\; (x,\; z)\; =\; E\; oe\; -\; jkz\; F\; r\; (\infty )\; -\; F\; r\; (2\; \lambda \; z\; (h\; -\; x))\; F\; r\; (\infty )\; -\; F\; r\; (\; -\; \infty )\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{E\}\}\; (x,\; z)\; =\; E\_\; \{o\}\; e\; ^\; \{-\; jkz\}\; \{\backslash \; frac\; \{Fr\; (\backslash \; infty)\; -Fr\; (\{\backslash \; sqrt\; \{\backslash \; frac\; \{2\})\; \{\backslash \; lambda\; z\}\}\}\; (hx))\}\; \{Fr\; (\backslash \; infty)\; -Fr\; (-\; \backslash \; infty)\}\}\}$,

где $F\; r\; (x)\; \{\backslash \; displaystyle\; Fr\; (x)\}$- интегральная функция Френеля, которая образует спираль Корню на комплексной плоскости.

Итак, чтобы упростить расчет затухания плоской волны при ее дифрагировании от острия ножа, можно использовать диаграмму спирали Корню, представив величины $F\; r\; (a)\; -\; F\; r\; (b)\; \{\backslash \; displaystyle\; Fr\; (a)\; -Fr\; (b)\}$как физические расстояния между точками, представленные $F\; r\; (a)\; \{\backslash \; displaystyle\; Fr\; (a)\}$и $F\; r\; (b)\; \{\backslash \; displaystyle\; Fr\; (b)\}$для соответствующих $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$. Это облегчает грубое вычисление затухания плоской волны на острие высоты $h\; \{\backslash \; displaystyle\; h\}$в местоположении $(x,\; z)\; \{\backslash \; displaystyle\; (x,\; z)\}$за острием ножа.

Интегральная оптика

Изгибы с непрерывно изменяющимся радиусом кривизны, следующие по спирали Эйлера, также используются для снижения потерь в фотонных интегральных схемах, либо в одномодовых волноводах, чтобы сгладить резкое изменение кривизны и связь с модами излучения, или в многомодовых волноводах, чтобы подавить связь с модами более высокого порядка и обеспечить эффективную одномодовую работу. Новаторское и очень элегантное применение спирали Эйлера к волноводам было сделано еще в 1957 году с полым металлическим волноводом для микроволн. Идея заключалась в том, чтобы использовать тот факт, что прямой металлический волновод можно физически согнуть, чтобы естественным образом принять форму постепенного изгиба, напоминающую спираль Эйлера.

Автогонки

Автор автоспорта Адам Бруйяр продемонстрировал использование спирали Эйлера для оптимизации гоночной трассы на участке входа в поворот.

Типографика и цифровая векторная графика

Raph Levien выпустил Spiro в качестве инструментария для дизайна кривых, особенно шрифтов, в 2007 году под бесплатной лицензией. Этот набор инструментов был довольно быстро реализован впоследствии в инструменте разработки шрифтов Fontforge и цифровом векторном рисунке Inkscape.

Картографическая проекция

Вырезание сферы по спирали шириной 1 / N и сглаживание получившейся формы дает спираль Эйлера, когда N стремится к бесконечности. Если сфера является глобусом, это создает проекцию карты, искажение которой стремится к нулю, когда N стремится к бесконечности.

Форма усов

Естественные формы вибрисс мистициальных подушечек крысы (усы ) хорошо аппроксимируются кусочками спирали Эйлера. Когда все эти части одной крысы собраны вместе, они охватывают интервал, простирающийся от одной спиральной области спирали Эйлера до другой.

Символы

$R\; \{\backslash \; displaystyle\; R\}$	Радиус кривизны
$R\; c\; \{\backslash \; displaystyle\; R\_\; \{c\}\}$	Радиус круговой кривой в конце спирали
$\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$	Угол кривой от начала спирали (бесконечное $R\; \{\backslash \; displaystyle\; R\}$) до определенной точки спирали.
	Это также можно измерить как угол между начальной касательной и касательной в соответствующей точке.
$\theta \; s\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{s\}\}$	Угол полной спиральной кривой
$L,\; s\; \{\backslash \; displaystyle\; L,\; s\}$	Длина, измеренная вдоль спиральной кривой от ее исходного положения
$L\; s,\; поэтому\; \{\backslash \; displaystyle\; L\_\; \{s\},\; s\_\; \{o\}\}$	Длина спиральной кривой

Выведение

На графике справа показана спираль Эйлера, используемая в качестве кривой сервитута (перехода) между двумя заданными кривыми, в данном случае прямой линией (отрицательная ось x) и окружностью. Спираль начинается в начале координат в положительном направлении x и постепенно поворачивается против часовой стрелки, касаясь окружности. Спираль - это небольшой сегмент двухконцевой спирали Эйлера в первом квадранте. Из определения кривизны: $1\; R\; =\; d\; \theta \; ds\; \propto \; s\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{R\}\}\; =\; \{\backslash \; frac\; \{d\; \backslash \; theta\}\; \{ds\}\}\; \backslash \; propto\; s\; \}$ т.е. $R\; s\; =\; константа\; =\; R\; cso\; \{\backslash \; displaystyle\; Rs\; =\; \{\backslash \; text\; \{constant\}\}\; =\; R\_\; \{c\}\; s\_\; \{o\}\}$ $d\; \theta \; ds\; =\; s\; R\; cso\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; theta\}\; \{ds\}\}\; =\; \{\backslash \; frac\; \{s\}\; \{R\_\; \{c\}\; s\_\; \{o\}\}\}\}$ Мы пишем в формате, $d\; \theta \; ds\; =\; 2\; a\; 2\; s\; \{\backslash \; displaystyle\; \{\; \backslash \; frac\; \{d\; \backslash \; theta\}\; \{ds\}\}\; =\; 2a\; ^\; \{2\}\; s\}$ Где $2\; a\; 2\; =\; 1\; R\; cso\; \{\backslash \; displaystyle\; 2a\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{1\}\; \{R\_\; \{c\}\; s\_\; \{o\}\}\}\}$ Или $a\; =\; 1\; 2\; R\; cso\; \{\backslash \; displaystyle\; a\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2R\_\; \{c\}\; s\_\; \{o\}\}\}\}\}$ Таким образом, $\theta \; =\; (as)\; 2\; \{\backslash \; displaystyle\; \backslash \; theta\; =\; (as)\; ^\; \{2\}\}$ Теперь $x\; =\; \int \; 0\; L\; cos\; \; \theta \; ds\; =\; \int \; 0\; L\; cos\; \; [\; (as)\; 2]\; ds\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; x\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\}\; \backslash \; cos\; \backslash \; theta\; \backslash ,\; ds\; \backslash \backslash \; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\}\; \backslash \; cos\; \backslash \; left\; [(as)\; ^\; \{2\}\; \backslash \; right]\; ds\; \backslash \; end\; \{align\}\}\}$ Если $s\; \prime \; =\; as\; \{\backslash \; displaystyle\; s\; \text{'}=\; as\}$ Тогда $ds\; =\; ds\; \prime \; A\; \{\backslash \; displaystyle\; ds\; =\; \{\backslash \; frac\; \{ds\; \text{'}\}\; \{a\}\}\}$ Таким образом, $x\; =\; 1\; a\; \int \; 0\; L\; \prime \; cos\; \; s\; 2\; ds\; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; frac\; \{1\}\; \{a\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\; \text{'}\}\; \backslash \; cos\; \{s\}\; ^\; \{2\}\; ds\}$ $y\; =\; \int \; 0\; L\; sin\; \; \theta \; ds\; =\; \int \; 0\; L\; sin\; \; [(as)\; 2]\; ds\; знак\; равно\; 1\; a\; \int \; 0\; L\; \text{'}грех\; \; s\; 2\; ds\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнен\}\; y\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\}\; \backslash \; sin\; \backslash \; theta\; \backslash ,\; ds\; \backslash \backslash \; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\}\; \backslash \; sin\; \backslash \; left\; [(as)\; ^\; \{2\}\; \backslash \; справа]\; ds\; \backslash \backslash \; =\; \{\backslash \; frac\; \{1\}\; \{a\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\; \text{'}\}\; \backslash \; sin\; \{s\}\; ^\; \{2\}\; \backslash ,\; ds\; \backslash \; end\; \{align\}\}\}$

Разложение интеграла Френеля

Если a = 1, что имеет место для нормализованной кривой Эйлера, то декартовы координаты задаются интегралами Френеля (или интегралами Эйлера):

$C\; (L)\; =\; \int \; 0\; L\; соз\; \; (s\; 2)\; ds\; S\; (L)\; знак\; равно\; \int \; 0\; L\; грех\; \; (s\; 2)\; ds\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; C\; (L)\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\}\; \backslash \; cos\; (\; s\; ^\; \{2\})\; \backslash ,\; ds\; \backslash \backslash \; S\; (L)\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\}\; \backslash \; sin\; (s\; ^\; \{2\})\; \backslash ,\; ds\; \backslash \; end\; \{align\}\}\}$

Нормализация и заключение

Для данной кривой Эйлера с:

$2\; RL\; =\; 2\; R\; c\; L\; s\; =\; 1\; a\; 2\; \{\backslash \; displaystyle\; 2RL\; =\; 2R\_\; \{c\}\; L\_\; \{s\}\; =\; \{\backslash \; frac\; \{1\}\; \{a\; ^\; \{2\}\}\}\}$

или

$1\; R\; =\; LR\; c\; L\; s\; =\; 2\; a\; 2\; L\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{R\}\}\; =\; \{\backslash \; frac\; \{L\}\; \{R\_\; \{c\}\; L\_\; \{s\}\}\}\; =\; 2a\; ^\; \{2\}\; L\}$

, тогда

$x\; =\; 1\; a\; \int \; 0\; L\; \prime \; cos\; \; s\; 2\; ds\; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; frac\; \{1\}\; \{a\; \}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\; \text{'}\}\; \backslash \; cos\; s\; ^\; \{2\}\; \backslash ,\; ds\}$

$y\; =\; 1\; a\; \int \; 0\; L\; \prime \; sin\; \; s\; 2\; ds\; \{\backslash \; displaystyle\; y\; =\; \{\backslash \; frac\; \{1\; \}\; \{a\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\; \text{'}\}\; \backslash \; sin\; s\; ^\; \{2\}\; \backslash ,\; ds\}$

где $L\; \prime \; =\; a\; L\; \{\backslash \; displaystyle\; L\; \text{'}=\; aL\}$и $a\; =\; 1\; 2\; R\; c\; L\; s\; \{\backslash \; displaystyle\; a\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2R\_\; \{c\}\; L\_\; \{s\}\}\}\}\}$.

Таким образом, процесс получения решения (x, y) спирали Эйлера можно описать как:

• Отображение L исходной спирали Эйлера путем умножения на множитель a в L ′ нормализованной спирали Эйлера;
• Найти (x ′, y ′) из интегралов Френеля; и
• Сопоставить (x ′, y ′) с (x, y) путем увеличения (денормализации) с коэффициентом $1\; /\; a\; \{\backslash \; displaystyle\; 1\; /\; a\}$. Обратите внимание, что $1\; /\; a>1\; \{\backslash \; displaystyle\; 1\; /\; a>1\}$.

В процессе нормализации

$R\; c\; \prime \; =\; R\; c\; 2\; R\; c\; L\; s\; =\; R\; c\; 2\; L\; s\; \{\backslash \; displaystyle\; \{\; \backslash \; begin\; \{align\}\; R\; \text{'}\_\; \{c\}\; =\; \{\backslash \; frac\; \{R\_\; \{c\}\}\; \{\backslash \; sqrt\; \{2R\_\; \{c\}\; L\_\; \{s\}\}\}\}\; \backslash \backslash \; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{R\_\; \{\; c\}\}\; \{2L\_\; \{s\}\}\}\}\; \backslash \backslash \backslash \; конец\; \{выровнено\}\}\}$

$L\; s\; \prime \; =\; L\; s\; 2\; R\; c\; L\; s\; =\; L\; s\; 2\; R\; c\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; L\; \text{'}\_\; \{s\}\; =\; \{\backslash \; frac\; \{L\_\; \{s\}\}\; \{\backslash \; sqrt\; \{2R\_\; \{c\}\; L\_\; \{s\}\}\}\}\; \backslash \backslash \; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{L\_\; \{s\}\}\; \{2R\_\; \{\; c\}\}\}\}\; \backslash \; end\; \{align\}\}\}$

Тогда

$2\; R\; c\; \prime \; L\; s\; \prime \; =\; 2\; R\; c\; 2\; L\; s\; L\; s\; 2\; R\; c\; =\; 2\; 2\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{\; выровнено\}\; 2R\; \text{'}\_\; \{c\}\; L\text{'}\; \_\; \{s\}\; =\; 2\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{R\_\; \{c\}\}\; \{2L\_\; \{s\}\}\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{L\_\; \{s\}\}\; \{\; 2R\_\; \{c\}\}\}\}\; \backslash \backslash \; =\; \{\backslash \; tfrac\; \{2\}\; \{2\}\}\; \backslash \backslash \; =\; 1\; \backslash \; end\; \{align\}\}\}$

Обычно нормализация уменьшает L 'до небольшого значения (<1) and results in good converging characteristics of the Fresnel integral manageable with only a few terms (at a price of increased числовая нестабильность расчета, особенно для больших $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$значений.).

.

Иллюстрация

Дано:

$R\; c\; =\; 300\; м\; L\; s\; =\; 100\; м\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; R\_\; \{c\}\; =\; 300\; \{\backslash \; t\_dv\; \{m\}\}\; \backslash \backslash \; L\_\; \{s\}\; =\; 100\; \{\backslash \; t\_dv\; \{m\}\}\; \backslash \; конец\; \{выровнен\}\}\}$

Тогда

$\theta \; s\; =\; L\; s\; 2\; R\; c\; =\; 100\; 2\; \times \; 300\; =\; 0,1667\; радиан\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; theta\; \_\; \{s\}\; =\; \{\backslash \; frac\; \{\; L\_\; \{s\}\}\; \{2R\_\; \{c\}\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{100\}\; \{2\; \backslash \; times\; 300\}\}\; \backslash \backslash \; =\; 0,1667\; \backslash \; \{\backslash \; t\_dv\; \{радиан\}\}\; \backslash \backslash \backslash \; конец\; \{выровнено\}\}\; \}$

И

$2\; R\; c\; L\; s\; =\; 60\; 000\; \{\backslash \; displaystyle\; 2R\_\; \{c\}\; L\_\; \{s\}\; =\; 60\; 000\}$

Мы уменьшаем спираль Эйлера на √60 000, т.е. 100√6 до нормализованного Спираль Эйлера, имеющая:

$R\; c\; \text{'}=\; 3\; 6\; м\; L\; s\text{'}\; =\; 1\; 6\; м\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; R\; \text{'}\_\; \{c\}\; =\; \{\backslash \; tfrac\; \{3\}\; \{\backslash \; sqrt\; \{6\}\; \}\}\; \{\backslash \; t\_dv\; \{m\}\}\; \backslash \backslash \; L\; \text{'}\_\; \{s\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{\backslash \; sqrt\; \{6\}\}\}\; \{\backslash \; t\_dv\; \{m\}\}\; \backslash \backslash \backslash \backslash \backslash \; конец\; \{выровнено\}\}\}$

$2\; R\; c\; \prime \; L\; s\; \prime \; =\; 2\; \times \; 3\; 6\; \times \; 1\; 6\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; 2R\; \text{'}\_\; \{c\}\; L\text{'}\; \_\; \{s\}\; =\; 2\; \backslash \; times\; \{\backslash \; tfrac\; \{\; 3\}\; \{\backslash \; sqrt\; \{6\}\}\}\; \backslash \; times\; \{\backslash \; tfrac\; \{1\}\; \{\backslash \; sqrt\; \{6\}\}\}\; \backslash \backslash \; =\; 1\; \backslash \; end\; \{align\}\}\}$

И

$\theta \; s\; =\; L\; s\; \prime \; 2\; R\; c\; \prime \; =\; 1\; 6\; 2\; \times \; 3\; 6\; =\; 0,1667\; радиан\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; theta\; \_\; \{s\}\; =\; \{\backslash \; frac\; \{L\; \text{'}\_\; \{s\}\}\; \{2R\text{'}\; \_\; \{c\}\; \}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{\backslash \; tfrac\; \{1\}\; \{\backslash \; sqrt\; \{6\}\}\}\; \{2\; \backslash \; times\; \{\backslash \; tfrac\; \{3\; \}\; \{\backslash \; sqrt\; \{6\}\}\}\}\}\; \backslash \backslash \; =\; 0,1667\; \backslash \; \{\backslash \; t\_dv\; \{radian\}\}\; \backslash \backslash \backslash \; end\; \{align\}\}\}$

Два угла $\theta \; s\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{s\}\}$такие же. Таким образом, это подтверждает, что исходная и нормализованная спирали Эйлера геометрически подобны. Геометрическое место нормализованной кривой может быть определено с помощью интеграла Френеля, а геометрическое место исходной спирали Эйлера может быть получено путем масштабирования назад / вверх или денормализации.

Другие свойства нормализованных спиралей Эйлера

Нормализованные спирали Эйлера могут быть выражены как:

$x\; =\; \int \; 0\; L\; cos\; \; s\; 2\; ds\; \{\backslash \; displaystyle\; x\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\}\; \backslash \; cos\; s\; ^\; \{2\}\; ds\}$

$y\; =\; \int \; 0\; L\; sin\; \; s\; 2\; ds\; \{\backslash \; displaystyle\; y\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\}\; \backslash \; sin\; s\; ^\; \{2\}\; ds\}$

Или выражается как степенной ряд :

$x\; =\; \sum \; i\; =\; 0\; \infty \; (-\; 1)\; i\; (2\; i)!\; s\; 4\; i\; +\; 1\; 4\; i\; +\; 1\; |\; 0\; L\; знак\; равно\; \sum \; я\; знак\; равно\; 0\; \infty \; (-\; 1)\; я\; (2\; я)!\; L\; 4\; я\; +\; 1\; 4\; я\; +\; 1\; \{\backslash \; displaystyle\; x\; =\; \backslash \; left.\; \backslash \; Sum\; \_\; \{i\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{i\}\}\; \{(2i)!\}\}\; \{\backslash \; frac\; \{s\; ^\; \{4i\; +\; 1\}\}\; \{4i\; +\; 1\}\}\; \backslash \; right\; |\; \_\; \{0\}\; ^\; \{L\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{i\}\}\; \{(2i)!\}\}\; \{\backslash \; frac\; \{L\; ^\; \{4i\; +\; 1\}\}\; \{4i\; +\; 1\}\}\}$

$y\; =\; \sum \; i\; =\; 0\; \infty \; (-\; 1)\; i\; (2\; i\; +\; 1)!\; с\; 4\; я\; +\; 3\; 4\; я\; +\; 3\; |\; 0\; L\; знак\; равно\; \sum \; я\; знак\; равно\; 0\; \infty \; (-\; 1)\; я\; (2\; я\; +\; 1)!\; L\; 4\; я\; +\; 3\; 4\; я\; +\; 3\; \{\backslash \; displaystyle\; y\; =\; \backslash \; left.\; \backslash \; Sum\; \_\; \{i\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{i\}\}\; \{(2i\; +\; 1)!\; \}\}\; \{\backslash \; frac\; \{s\; ^\; \{4i\; +\; 3\}\}\; \{4i\; +\; 3\}\}\; \backslash \; right\; |\; \_\; \{0\}\; ^\; \{L\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(\; -1)\; ^\; \{i\}\}\; \{(2i\; +\; 1)!\}\}\; \{\backslash \; Frac\; \{L\; ^\; \{4i\; +\; 3\}\}\; \{4i\; +\; 3\}\}\}$

Нормализованная спираль Эйлера сходится к одной точке в предел, который может быть выражен как:

$x\; \prime \; =\; lim\; L\; \to \; \infty \; \int \; 0\; L\; cos\; \; (s\; 2)\; ds\; =\; 1\; 2\; \pi \; 2\; \approx \; 0,6267\; \{\backslash \; displaystyle\; x\; ^\; \{\backslash \; prime\}\; =\; \backslash \; lim\; \_\; \{\; L\; \backslash \; to\; \backslash \; infty\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\}\; \backslash \; cos\; (s\; ^\; \{2\})\; ds\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\; \}\}\; \backslash \; приблизительно\; 0,6267\}$

$y\; \prime \; =\; lim\; L\; \to \; \infty \; \int \; 0\; L\; sin\; \; (s\; 2)\; ds\; =\; 1\; 2\; \pi \; 2\; \approx \; 0,6267\; \{\backslash \; displaystyle\; y\; ^\; \{\backslash \; prime\}\; =\; \backslash \; lim\; \_\; \{L\; \backslash \; to\; \backslash \; infty\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\}\; \backslash \; sin\; (s\; ^\; \{2\})\; ds\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\}\; \backslash \; приблизительно\; 0,6267\}$

Нормализованные спирали Эйлера обладают следующими свойствами:

$2\; R\; c\; L\; s\; =\; 1\; \{\backslash \; displaystyle\; 2R\_\; \{c\}\; L\_\; \{s\}\; =\; 1\}$

$\theta \; s\; =\; L\; s\; 2\; R\; c\; =\; L\; s\; 2\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{s\}\; =\; \{\backslash \; frac\; \{L\_\; \{s\}\}\; \{2R\_\; \{c\}\}\}\; =\; L\_\; \{s\}\; ^\; \{2\}\}$

и

$\theta \; =\; \theta \; s\; \cdot \; L\; 2\; L\; s\; 2\; знак\; равно\; L\; 2\; \{\backslash \; Displaystyle\; \backslash \; theta\; =\; \backslash \; theta\; \_\; \{s\}\; \backslash \; cdot\; \{\backslash \; frac\; \{L\; ^\; \{2\}\}\; \{L\_\; \{s\}\; ^\; \{2\}\; \}\}\; =\; L\; ^\; \{2\}\}$

$1\; R\; =\; d\; \theta \; d\; L\; =\; 2\; L\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{R\}\}\; =\; \{\backslash \; frac\; \{d\; \backslash \; theta\}\; \{dL\}\}\; =\; 2L\; \}$

Обратите внимание, что $2\; R\; c\; L\; s\; =\; 1\; \{\backslash \; displaystyle\; 2R\_\; \{c\}\; L\_\; \{s\}\; =\; 1\}$также означает $1\; /\; R\; c\; =\; 2\; L\; s\; \{\; \backslash \; displaystyle\; 1\; /\; R\_\; \{c\}\; =\; 2L\_\; \{s\}\}$в соответствии с последним математическим утверждением.

Следующий код SageMath создает второй график выше. Первые четыре строки выражают компонент спирали Эйлера. Функции Френеля найти не удалось. Вместо этого приняты интегралы двух расширенных рядов Тейлора. Остающийся код выражает, соответственно, касательную и окружность, включая вычисление координат центра.

var ('L') p = интеграл (taylor (cos (L ^ 2), L, 0, 12), L) q = интеграл (taylor (sin (L ^ 2), L, 0, 12), L) r1 = параметрический_площадь ([p, q], (L, 0, 1), color = 'красный') r2 = line ([(- 1.0, 0), (0,0)], rgbcolor = 'синий ') x1 = p.subs (L = 1) y1 = q.subs (L = 1) R = 0,5 x2 = x1 - R * sin (1.0) y2 = y1 + R * cos (1.0) r3 = circle (( x2, y2), R, rgbcolor = 'green') show (r1 + r2 + r3, aspect_ratio = 1, axes = false)

Далее следует код Mathematica для компонента спирали Эйлера (it работает непосредственно в wolframalpha.com):

ParametricPlot [{FresnelC [Sqrt [2 / \ [Pi]] t] / Sqrt [2 / \ [Pi]]], FresnelS [Sqrt [2 / \ [Pi]] t ] / Sqrt [2 / \ [Pi]]}, {t, -10, 10}]

Далее следует код Xcas для компонента спирали Эйлера:

plotparam ( [int (cos (u ^ 2), u, 0, t), int (sin (u ^ 2), u, 0, t)], t, -4,4)

Ниже приводится SageMath код для полной двусторонней спирали Эйлера:

s = var ('s') Parametric_plot ((lambda s: numerical_integral (cos (x ** 2), 0, s) [0]), лямбда s: числовой_интеграл (sin (x ** 2), 0, s) [0]), (-3 * pi / 2, 3 * pi / 2))

Ниже приведен код JavaScript для рисования спирали Эйлера на элементе холста :

function drawEulerSpiral (canvas, T, N, scale) {ctx = canvas.getContext ("2d"); var dx, dy, t = 0, prev = {x: 0, y: 0}, current; var dt = T / N; ctx.beginPath (); а (N--) {dx = Math.cos (t * t) * dt; dy = Math.sin (t * t) * dt; t + = dt; текущий = {x: предыдущий x + dx, y: предыдущий y + dy}; ctx.lineTo (current.x * scale, current.y * scale); пред = текущий; } ctx.stroke (); } drawEulerSpiral (document.getElementById ("myCanvas"), 10,10000,100)

Ниже приводится код логотипа (язык программирования) для рисования спирали Эйлера с использованием спрайта черепахи.

rt 90 repeat 720 [fd 10 lt repcount]

• Архимедова спираль
• Интеграл Френеля
• Геометрический дизайн дорог
• Список спиралей
• Переходная кривая пути

Примечания

Источники

• Спираль Эйлера на 2-мерных математических кривых
• Интерактивный пример с JSXGraph
• Спиральная картографическая проекция Эйлера