Совместимость (механика)

редактировать

В механике сплошной среды, совместимаядеформация (или деформация ) тензорное поле в теле - это то уникальное тензорное поле, которое получается, когда тело подвергается непрерывному, однозначному, поле смещения. Совместимость - это исследование условий, при которых может быть гарантировано такое поле смещения. Условия совместимости являются частными случаями условий интегрируемости и были впервые выведены для линейной упругости Барре де Сен-Венаном в 1864 году и строго доказаны Бельтрами в 1886 году.

В описании континуума твердого тела мы представляем себе, что тело состоит из набора бесконечно малых объемов или материальных точек. Предполагается, что каждый объем соединен со своими соседями без каких-либо зазоров или перекрытий. Для обеспечения t При деформации сплошного тела зазоры / нахлёстки не возникают. Тело, которое деформируется без образования каких-либо зазоров / перекрытий, называется совместимым телом. Условия совместимости - это математические условия, которые определяют, оставит ли конкретная деформация тело в совместимом состоянии.

В контексте теории бесконечно малых деформаций эти условия эквивалентны к заявлению, что смещения в теле могут быть получены путем интегрирования деформаций. Такое интегрирование возможно, если тензор Сен-Венана (или тензор несовместимости) $R (ε) {\ displaystyle {\ boldsymbol {R}} ({\ boldsymbol {\ varepsilon}})}$ ${\boldsymbol {R}}({\boldsymbol {\varepsilon }})$ исчезает в односвязном теле, где $ε {\ displaystyle {\ boldsymbol {\ varepsilon}}}$ $\boldsymbol{\varepsilon}$ - тензор бесконечно малых деформаций и

R: = ∇ × (∇ × ε) = 0. {\ displaystyle {\ boldsymbol {R}}: = {\ boldsymbol {\ nabla}} \ times ({\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ varepsilon}}) = {\ boldsymbol {0}} ~.}

{\boldsymbol {R}}:={\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }})={\boldsymbol {0}}~.

Для конечных деформаций условия совместимости принимают форму

R: = ∇ × F = 0 {\ displaystyle {\ boldsymbol {R}}: = {\ boldsymbol {\ nabla }} \ times {\ boldsymbol {F}} = {\ boldsymbol {0}}}

{\boldsymbol {R}}:={\boldsymbol {\nabla }}\times {\boldsymbol {F}}={\boldsymbol {0}}

где $F {\ displaystyle {\ boldsymbol {F}}}$ ${\boldsymbol {F}}$ - это градиент деформации.

Содержание

1 Условия совместимости для бесконечно малых деформаций
- 1.1 2-мерные
- 1,2 3-хмерные
2 Условия совместимости для конечных деформаций
- 2.1 Условия совместимости для правых Коши-Грина тензор деформации
3 Общая проблема совместимости
- 3.1 Необходимые условия
- 3.2 Достаточные условия
4 Совместимость градиента деформации
5 Совместимость бесконечно малых деформаций
- 5.1 Необходимые условия
- 5.2 Достаточно условия
6 Совместимость для правого поля деформации Коши-Грина
- 6.1 Необходимые условия
- 6.2 Достаточные условия
7 См. Также
8 Ссылки
9 Внешние ссылки

Условия совместимости для бесконечно малых деформаций

Условия совместимости в линейной упругости получены, наблюдая, что существует шесть соотношений деформация-смещение, которые являются функциями только трех неизвестных смещений. Это говорит о том, что три смещения могут быть удалены из системы уравнений без потери информации. Полученные выражения в терминах только деформаций обеспечивают ограничения на возможные формы поля деформаций.

2-мерные

Для двумерных задач плоской деформации соотношения деформация-смещение следующие:

ε 11 = ∂ u 1 ∂ x 1; ε 12 = 1 2 [∂ u 1 ∂ x 2 + ∂ u 2 ∂ x 1]; ε 22 знак равно ∂ U 2 ∂ Икс 2 {\ Displaystyle \ varepsilon _ {11} = {\ cfrac {\ partial u_ {1}} {\ partial x_ {1}}} ~; ~~ \ varepsilon _ {12} = {\ cfrac {1} {2}} \ left [{\ cfrac {\ partial u_ {1}} {\ partial x_ {2}}} + {\ cfrac {\ partial u_ {2}} {\ partial x_ { 1}}} \ right] ~; ~~ \ varepsilon _ {22} = {\ cfrac {\ partial u_ {2}} {\ partial x_ {2}}}}

\varepsilon _{{11}}={\cfrac {\partial u_{1}}{\partial x_{1}}}~;~~\varepsilon _{{12}}={\cfrac {1}{2}}\left[{\cfrac {\partial u_{{1}}}{\partial x_{2}}}+{\cfrac {\partial u_{{2}}}{\partial x_{1}}}\right]~;~~\varepsilon _{{22}}={\cfrac {\partial u_{{2}}}{\partial x_{2}}}

Повторное дифференцирование этих отношений по порядку чтобы удалить смещения $u 1 {\ displaystyle u_ {1}}$ $u_{1}$ и $u 2 {\ displaystyle u_ {2}}$ $u_{2}$ , дает нам двумерный условие совместимости деформаций

∂ 2 ε 11 ∂ x 2 2 - 2 ∂ 2 ε 12 ∂ x 1 ∂ x 2 + ∂ 2 ε 22 ∂ x 1 2 = 0 {\ displaystyle {\ cfrac {\ partial ^ {2 } \ varepsilon _ {11}} {\ partial x_ {2} ^ {2}}} - 2 {\ cfrac {\ partial ^ {2} \ varepsilon _ {12}} {\ partial x_ {1} \ partial x_ {2}}} + {\ cfrac {\ partial ^ {2} \ varepsilon _ {22}} {\ partial x_ {1} ^ {2}}} = 0}

{\cfrac {\partial ^{2}\varepsilon _{{11}}}{\partial x_{2}^{2}}}-2{\cfrac {\partial ^{2}\varepsilon _{{12}}}{\partial x_{1}\partial x_{2}}}+{\cfrac {\partial ^{2}\varepsilon _{{22}}}{\partial x_{1}^{2}}}=0

Единственное поле смещения, которое разрешено совместимое поле плоской деформации - это поле смещения плоскости, т. е. $u = u (x 1, x 2) {\ displaystyle \ mathbf {u} = \ mathbf {u} (x_ {1}, x_ {2})}$ ${\mathbf {u}}={\mathbf {u}}(x_{1},x_{2})$ .

3-х мерный

В трех измерениях, в дополнение к еще двум уравнениям в форме двух измерений, есть еще три уравнения вида

∂ 2 ε 33 ∂ x 1 ∂ x 2 = ∂ ∂ x 3 [∂ ε 23 ∂ x 1 + ∂ ε 31 ∂ x 2 - ∂ ε 12 ∂ x 3] {\ displaystyle {\ cfrac {\ partial ^ {2} \ varepsilon _ {33}} {\ partial x_ {1} \ partial x_ {2}}} = {\ cfrac {\ partial} {\ partial x_ {3}}} \ left [{ \ cfrac {\ partial \ varepsilon _ {23}} {\ partial x_ {1}}} + {\ cfrac {\ partial \ varepsilon _ {31}} {\ partial x_ {2}}} - {\ cfrac {\ partial \ varepsilon _ {12}} {\ partial x_ {3}}} \ right]}

{\cfrac {\partial ^{2}\varepsilon _{{33}}}{\partial x_{1}\partial x_{2}}}={\cfrac {\partial }{\partial x_{3}}}\left[{\cfrac {\partial \varepsilon _{{23}}}{\partial x_{1}}}+{\cfrac {\partial \varepsilon _{{31}}}{\partial x_{2}}}-{\cfrac {\partial \varepsilon _{{12}}}{\partial x_{3}}}\right]

Следовательно, существует 3 = 81 дифференциальное уравнение в частных производных, однако из-за условий симметрии это число сокращается до шести разные условия совместимости. Мы можем записать эти условия в индексном обозначении как

eikrejls ε ij, kl = 0 {\ displaystyle e_ {ikr} ~ e_ {jls} ~ \ varepsilon _ {ij, kl} = 0}

e_{{ikr}}~e_{{jls}}~\varepsilon _{{ij,kl}}=0

где $eijk {\ displaystyle e_ {ijk}}$ $e_{ijk}$ - символ перестановки . В прямой тензорной записи

∇ × (∇ × ε) = 0 {\ displaystyle {\ boldsymbol {\ nabla}} \ times ({\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ varepsilon}}) = {\ boldsymbol {0}}}

{\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }})={\boldsymbol {0}}

где оператор curl может быть выражен в ортонормированной системе координат как $∇ × ε = eijk ε rj, iek ⊗ er {\ displaystyle {\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ varepsilon}} = e_ {ijk} \ varepsilon _ {rj, i} \ mathbf {e} _ {k} \ otimes \ mathbf {e} _ {r}}$ ${\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }}=e_{{ijk}}\varepsilon _{{rj,i}}{\mathbf {e}}_{k}\otimes {\mathbf {e}}_{r}$ .

Второй порядок тензор

R: = ∇ × (∇ × ε); R rs: = eikrejls ε ij, kl {\ displaystyle {\ boldsymbol {R}}: = {\ boldsymbol {\ nabla}} \ times ({\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ varepsilon}}) ~; ~~ R_ {rs}: = e_ {ikr} ~ e_ {jls} ~ \ varepsilon _ {ij, kl}}

{\boldsymbol {R}}:={\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }})~;~~R_{{rs}}:=e_{{ikr}}~e_{{jls}}~\varepsilon _{{ij,kl}}

известен как тензор несовместимости и эквивалентен тензор совместимости Сен-Венана

Условия совместимости для конечных деформаций

Для твердых тел, в которых не требуется, чтобы деформации были малыми, условия совместимости принимают вид

∇ × F = 0 {\ displaystyle {\ boldsymbol {\ nabla}} \ times {\ boldsymbol {F}} = {\ boldsymbol {0}}}

{\boldsymbol {\nabla }}\times {\boldsymbol {F}}={\boldsymbol {0}}

где $F {\ displaystyle {\ boldsymbol {F}}}$ ${\boldsymbol {F}}$ - это градиент деформации. В терминах компонентов в декартовой системе координат мы можем записать эти отношения совместимости как

e ABC ∂ F i B ∂ XA = 0 {\ displaystyle e_ {ABC} ~ {\ cfrac {\ partial F_ {iB}} {\ partial X_ {A}}} = 0}

e_{{ABC}}~{\cfrac {\partial F_{{iB}}}{\partial X_{A}}}=0

Это условие необходимо, если деформация должна быть непрерывной и получена из отображения $x = χ (X, t) {\ displaystyle \ mathbf {x} = {\ boldsymbol {\ chi}} (\ mathbf {X}, t)}$ ${\mathbf {x}}={\boldsymbol {\chi }}({\mathbf {X}},t)$ (см. Теория конечных деформаций ). Это же условие также достаточно для обеспечения совместимости в односвязном теле.

Условие совместимости для правого тензора деформации Коши-Грина

Условие совместимости для правого тензора деформации Коши-Грина можно выразить как

R α β ρ γ: знак равно ∂ ∂ X ρ [Γ α β γ] - ∂ ∂ X β [Γ α ρ γ] + Γ μ ρ γ Γ α β μ - Γ μ β γ Γ α ρ μ = 0 {\ Displaystyle R _ {\ альфа \ бета \ rho} ^ {\ gamma}: = {\ frac {\ partial} {\ partial X ^ {\ rho}}} [\ Gamma _ {\ alpha \ beta} ^ {\ gamma}] - {\ гидроразрыв {\ partial} {\ partial X ^ {\ beta}}} [\ Gamma _ {\ alpha \ rho} ^ {\ gamma}] + \ Gamma _ {\ mu \ rho} ^ {\ gamma} ~ \ Gamma _ {\ alpha \ beta} ^ {\ mu} - \ Gamma _ {\ mu \ beta} ^ {\ gamma} ~ \ Gamma _ {\ alpha \ rho} ^ {\ mu} = 0}

R_{{\alpha \beta \rho }}^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\Gamma _{{\alpha \beta }}^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\Gamma _{{\alpha \rho }}^{\gamma }]+\Gamma _{{\mu \rho }}^{\gamma }~\Gamma _{{\alpha \beta }}^{\mu }-\Gamma _{{\mu \beta }}^{\gamma }~\Gamma _{{\alpha \rho }}^{\mu }=0

где $Γ ijk {\ displaystyle \ Gamma _ {ij} ^ {k}}$ $\Gamma^k_{ij}$ - это символ Кристоффеля второго рода. Величина $R ijkm {\ displaystyle R_ {ijk} ^ {m}}$ $R_{{ijk}}^{m}$ представляет смешанные компоненты тензора кривизны Римана-Кристоффеля.

Общая проблема совместимости

Проблема совместимости в механике сплошных сред включает определение допустимых однозначных непрерывных полей на односвязных телах. Точнее, проблему можно сформулировать следующим образом.

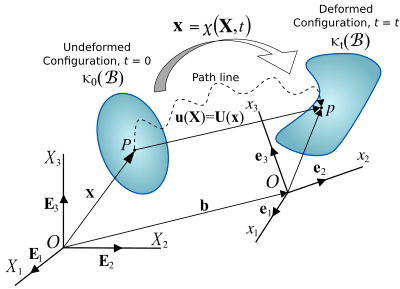
Рис. 1. Движение сплошного тела.

Рассмотрим деформацию тела, показанного на рисунке 1. Если мы выразим все векторы через опорную координату система ${(E 1, E 2, E 3), O} {\ displaystyle \ {(\ mathbf {E} _ {1}, \ mathbf {E} _ {2}, \ mathbf {E} _ {3}), O \}}$ $\{({\mathbf {E}}_{1},{\mathbf {E}}_{2},{\mathbf {E}}_{3}),O\}$ , смещение точки в теле задается как

u = x - X; ui = xi - X i {\ displaystyle \ mathbf {u} = \ mathbf {x} - \ mathbf {X} ~; ~~ u_ {i} = x_ {i} -X_ {i}}

{\mathbf {u}}={\mathbf {x}}-{\mathbf {X}}~;~~u_{i}=x_{i}-X_{i}

Также

∇ u = ∂ u ∂ X; ∇ Икс знак равно ∂ Икс ∂ Икс {\ Displaystyle {\ boldsymbol {\ nabla}} \ mathbf {u} = {\ frac {\ partial \ mathbf {u}} {\ partial \ mathbf {X}}} ~; ~~ {\ boldsymbol {\ nabla}} \ mathbf {x} = {\ frac {\ partial \ mathbf {x}} {\ partial \ mathbf {X}}}}

{\boldsymbol {\nabla }}{\mathbf {u}}={\frac {\partial {\mathbf {u}}}{\partial {\mathbf {X}}}}~;~~{\boldsymbol {\nabla }}{\mathbf {x}}={\frac {\partial {\mathbf {x}}}{\partial {\mathbf {X}}}}

Какие условия для данного тензорного поля второго порядка $A (X) {\ displaystyle {\ boldsymbol {A}} (\ mathbf {X})}$ ${\boldsymbol {A}}({\mathbf {X}})$ на теле необходимы и достаточны, чтобы существовало уникальное векторное поле $v (Икс) {\ Displaystyle \ mathbf {v} (\ mathbf {X})}$ ${\mathbf {v}}({\mathbf {X}})$ , который удовлетворяет

∇ v = A ≡ vi, j = A ij {\ displaystyle {\ boldsymbol {\ nabla }} \ mathbf {v} = {\ boldsymbol {A}} \ quad \ Equiv \ quad v_ {i, j} = A_ {ij}}

{\boldsymbol {\nabla }}{\mathbf {v}}={\boldsymbol {A}}\quad \equiv \quad v_{{i,j}}=A_{{ij}}

Необходимые условия

В качестве необходимых условий принимаем что поле $v {\ displaystyle \ mathbf {v}}$ $\mathbf {v}$ существует и удовлетворяет $vi, j = A ij {\ displaystyle v_ {i, j} = A_ {ij}}$ $v_{{i,j}}=A_{{ij}}$ . Тогда

v i, j k = A i j, k; vi, kj = A ik, j {\ displaystyle v_ {i, jk} = A_ {ij, k} ~; ~~ v_ {i, kj} = A_ {ik, j}}

v_{{i,jk}}=A_{{ij,k}}~;~~v_{{i,kj}}=A_{{ik,j}}

Поскольку изменение порядка дифференцирование не влияет на результат, который мы имеем

vi, jk = vi, kj {\ displaystyle v_ {i, jk} = v_ {i, kj}}

v_{{i,jk}}=v_{{i,kj}}

Следовательно,

A ij, k = A ik, j {\ displaystyle A_ {ij, k} = A_ {ik, j}}

A_{{ij,k}}=A_{{ik,j}}

Из известного тождества для ротора тензора получаем необходимое условие

∇ × A = 0 {\ displaystyle {\ boldsymbol {\ nabla}} \ times {\ boldsymbol {A}} = {\ boldsymbol {0}}}

{\boldsymbol {\nabla }}\times {\boldsymbol {A}}={\boldsymbol {0}}

Достаточные условия

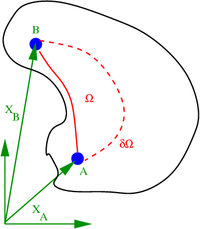
Рис. 2. Пути интеграции, используемые при доказательстве условий достаточности для совместимость.

Чтобы доказать, что этого условия достаточно, чтобы гарантировать существование совместимого тензорного поля второго порядка, мы начнем с предположения, что поле $A {\ displaystyle {\ boldsymbol {A}}}$ ${\boldsymbol {A}}$ существует такое, что $∇ × A = 0 {\ displaystyle {\ boldsymbol {\ nabla}} \ times {\ boldsymbol {A}} = {\ boldsymbol {0}}}$ ${\boldsymbol {\nabla }}\times {\boldsymbol {A}}={\boldsymbol {0}}$ . Мы интегрируем это поле, чтобы найти векторное поле $v {\ displaystyle \ mathbf {v}}$ $\mathbf {v}$ вдоль линии между точками $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ (см. Рисунок 2), то есть

v (XB) - v (XA) = ∫ XAXB ∇ v ⋅ d X = ∫ XAXBA (X) X d Икс {\ displaystyle \ mathbf {v} (\ mathbf {X} _ {B}) - \ mathbf {v} (\ mathbf {X} _ {A}) = \ int _ {\ mathbf {X} _ { A}} ^ {\ mathbf {X} _ {B}} {\ boldsymbol {\ nabla}} \ mathbf {v} \ cdot ~ d \ mathbf {X} = \ int _ {\ mathbf {X} _ {A }} ^ {\ mathbf {X} _ {B}} {\ boldsymbol {A}} (\ mathbf {X}) \ cdot d \ mathbf {X}}

{\mathbf {v}}({\mathbf {X}}_{B})-{\mathbf {v}}({\mathbf {X}}_{A})=\int _{{{\mathbf {X}}_{A}}}^{{{\mathbf {X}}_{B}}}{\boldsymbol {\nabla }}{\mathbf {v}}\cdot ~d{\mathbf {X}}=\int _{{{\mathbf {X}}_{A}}}^{{{\mathbf {X}}_{B}}}{\boldsymbol {A}}({\mathbf {X}})\cdot d{\mathbf {X}}

Если векторное поле $v {\ displaystyle \ mathbf {v}}$ $\mathbf {v}$ должен быть однозначным, тогда значение интеграла не должно зависеть от пути, взятого для перехода от $A {\ displaystyle A}$ $A$ по $B {\ displaystyle B}$ $B$ .

Из теоремы Стокса интеграл от тензора второго порядка вдоль замкнутого пути определяется как

∮ ∂ Ω A ⋅ ds = ∫ Ω п ⋅ (∇ × A) да {\ Displaystyle \ oint _ {\ partial \ Omega} { \ boldsymbol {A}} \ cdot d \ mathbf {s} = \ int _ {\ Omega} \ mathbf {n} \ cdot ({\ boldsymbol {\ nabla}} \ times {\ boldsymbol {A}}) ~ да }

\oint _{\partial \Omega }{\boldsymbol {A}}\cdot d\mathbf {s} =\int _{\Omega }\mathbf {n} \cdot ({\boldsymbol {\nabla }}\times {\boldsymbol {A}})~da

Используя предположение, что локон $A {\ displaystyle {\ boldsymbol {A}}}$ ${\boldsymbol {A}}$ равен нулю, мы получаем

∮ ∂ Ω A ⋅ ds = 0 ⟹ ∫ ABA ⋅ d Икс + ∫ BAA ⋅ d Икс знак равно 0 {\ displaystyle \ oint _ {\ partial \ Omega} {\ boldsymbol {A}} \ cdot d \ mathbf {s} = 0 \ quad \ подразумевает \ quad \ int _ {AB} {\ boldsymbol {A}} \ cdot d \ mathbf {X} + \ int _ {BA} {\ boldsymbol {A}} \ cdot d \ mathbf {X} = 0}

\oint _{\partial \Omega }{\boldsymbol {A}}\cdot d\mathbf {s} =0\quad \implies \quad \int _{AB}{\boldsymbol {A}}\cdot d\mathbf {X} +\int _{BA}{\boldsymbol {A}}\cdot d\mathbf {X} =0

Следовательно, интеграл равен не зависит от пути, и условия совместимости достаточно для обеспечения уникального поля $v {\ displaystyle \ mathbf {v}}$ $\mathbf {v}$ при условии, что тело просто подключено.

Совместимость градиента деформации

Условие совместимости градиента деформации получается непосредственно из приведенного выше доказательства путем наблюдения, что

F = ∂ x ∂ X = ∇ x {\ displaystyle { \ boldsymbol {F}} = {\ cfrac {\ partial \ mathbf {x}} {\ partial \ mathbf {X}}} = {\ boldsymbol {\ nabla}} \ mathbf {x}}

{\boldsymbol {F}}={\cfrac {\partial {\mathbf {x}}}{\partial {\mathbf {X}}}}={\boldsymbol {\nabla }}{\mathbf {x}}

Тогда необходимое и достаточными условиями существования совместимого поля $F {\ displaystyle {\ boldsymbol {F}}}$ ${\boldsymbol {F}}$ над односвязным телом являются

∇ × F = 0 {\ displaystyle {\ boldsymbol {\ nabla}} \ times {\ boldsymbol {F}} = {\ boldsymbol {0}}}

{\boldsymbol {\nabla }}\times {\boldsymbol {F}}={\boldsymbol {0}}

Совместимость бесконечно малых деформаций

Проблема совместимости малых деформаций может быть сформулирована следующим образом.

Дано симметричное тензорное поле второго порядка $ϵ {\ displaystyle {\ boldsymbol {\ epsilon}}}$ $\boldsymbol{\epsilon}$ , когда можно построить векторное поле $u {\ displaystyle \ mathbf {u}}$ $\mathbf {u}$ такой, что

ϵ = 1 2 [∇ u + (∇ u) T] {\ displaystyle {\ boldsymbol {\ epsilon}} = {\ frac {1} {2}} [{\ boldsymbol {\ nabla}} \ mathbf {u} + ({\ boldsymbol {\ nabla}} \ mathbf {u}) ^ {T}]}

{\boldsymbol {\epsilon }}={\frac {1}{2}}[{\boldsymbol {\nabla }}{\mathbf {u}}+({\boldsymbol {\nabla }}{\mathbf {u}})^{T}]

Необходимые условия

Предположим, что существует $u {\ displaystyle \ mathbf {u}}$ $\mathbf {u}$ такое, что выражение для $ϵ {\ displaystyle {\ boldsymbol {\ epsilon}}}$ $\boldsymbol{\epsilon}$ держит. Теперь

∇ u = ϵ + ω {\ displaystyle {\ boldsymbol {\ nabla}} \ mathbf {u} = {\ boldsymbol {\ epsilon}} + {\ boldsymbol {\ omega}}}

{\boldsymbol {\nabla }}{\mathbf {u}}={\boldsymbol {\epsilon }}+{\boldsymbol {\omega }}

, где

ω: = 1 2 [∇ u - (∇ u) T] {\ displaystyle {\ boldsymbol {\ omega}}: = {\ frac {1} {2}} [{\ boldsymbol {\ nabla}} \ mathbf {u} - ({\ boldsymbol {\ nabla}} \ mathbf {u}) ^ {T}]}

{\boldsymbol {\omega }}:={\frac {1}{2}}[{\boldsymbol {\nabla }}{\mathbf {u}}-({\boldsymbol {\nabla }}{\mathbf {u}})^{T}]

Следовательно, в индексной записи

∇ ω ≡ ω ij, k = 1 2 (ui, jk - uj, ik) знак равно 1 2 (ui, jk + uk, ji - uj, ik - uk, ji) = ε ik, j - ε jk, я {\ displaystyle {\ boldsymbol {\ nabla}} {\ полужирный символ {\ omega}} \ Equiv \ omega _ {ij, k} = {\ frac {1} {2}} (u_ {i, jk} -u_ {j, ik}) = {\ frac {1} { 2}} (u_ {i, jk} + u_ {k, ji} -u_ {j, ik} -u_ {k, ji}) = \ varepsilon _ {ik, j} - \ varepsilon _ {jk, i} }

{\boldsymbol {\nabla }}{\boldsymbol {\omega }}\equiv \omega _{{ij,k}}={\frac {1}{2}}(u_{{i,jk}}-u_{{j,ik}})={\frac {1}{2}}(u_{{i,jk}}+u_{{k,ji}}-u_{{j,ik}}-u_{{k,ji}})=\varepsilon _{{ik,j}}-\varepsilon _{{jk,i}}

Если $ω {\ displaystyle {\ boldsymbol {\ omega}}}$ ${\boldsymbol {\omega }}$ непрерывно дифференцируемо, мы имеем $ω ij, kl = ω ij, lk {\ displaystyle \ omega _ {ij, kl} = \ omega _ {ij, lk}}$ $\omega _{{ij,kl}}=\omega _{{ij,lk}}$ . Следовательно,

ε ik, jl - ε jk, il - ε il, jk + ε jl, ik = 0 {\ displaystyle \ varepsilon _ {ik, jl} - \ varepsilon _ {jk, il} - \ varepsilon _ {il, jk} + \ varepsilon _ {jl, ik} = 0}

\varepsilon _{{ik,jl}}-\varepsilon _{{jk,il}}-\varepsilon _{{il,jk}}+\varepsilon _{{jl,ik}}=0

В прямой тензорной записи

∇ × (∇ × ϵ) = 0 {\ displaystyle {\ boldsymbol {\ nabla}} \ times ( {\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ epsilon}}) = {\ boldsymbol {0}}}

{\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})={\boldsymbol {0}}

Вышеуказанные условия являются необходимыми. Если $w {\ displaystyle \ mathbf {w}}$ $\mathbf {w}$ является вектором бесконечно малого вращения, то $∇ × ϵ = ∇ w + ∇ w T {\ displaystyle {\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ epsilon}} = {\ boldsymbol {\ nabla}} \ mathbf {w} + {\ boldsymbol {\ nabla}} \ mathbf {w} ^ {T}}$ ${\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }}={\boldsymbol {\nabla }}{\mathbf {w}}+{\boldsymbol {\nabla }}{\mathbf {w}}^{T}$ . Следовательно, необходимое условие можно также записать как $∇ × (∇ w + ∇ w T) = 0 {\ displaystyle {\ boldsymbol {\ nabla}} \ times ({\ boldsymbol {\ nabla}} \ mathbf {w } + {\ boldsymbol {\ nabla}} \ mathbf {w} ^ {T}) = {\ boldsymbol {0}}}$ ${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}{\mathbf {w}}+{\boldsymbol {\nabla }}{\mathbf {w}}^{T})={\boldsymbol {0}}$ .

Достаточные условия

Предположим теперь, что условие $∇ × (∇ × ϵ) = 0 {\ displaystyle {\ boldsymbol {\ nabla}} \ times ({\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ epsilon}}) = {\ boldsymbol {0}} }$ ${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})={\boldsymbol {0}}$ выполняется в части тела. Достаточно ли этого условия, чтобы гарантировать существование непрерывного однозначного поля смещения $u {\ displaystyle \ mathbf {u}}$ $\mathbf {u}$ ?

Первый шаг в процессе - показать, что это условие подразумевает, что тензор бесконечно малого вращения $ω {\ displaystyle {\ boldsymbol {\ omega}}}$ ${\boldsymbol {\omega }}$ определен однозначно. Для этого мы интегрируем $∇ w {\ displaystyle {\ boldsymbol {\ nabla}} \ mathbf {w}}$ ${\boldsymbol {\nabla }}{\mathbf {w}}$ по пути $XA {\ displaystyle \ mathbf {X} _ { A}}$ ${\mathbf {X}}_{A}$ до $XB {\ displaystyle \ mathbf {X} _ {B}}$ ${\mathbf {X}}_{B}$ , т.е.

w (XB) - w (XA) = ∫ XAXB ∇ вес ⋅ d Икс знак равно ∫ XAXB (∇ × ϵ) ⋅ d X {\ displaystyle \ mathbf {w} (\ mathbf {X} _ {B}) - \ mathbf {w} (\ mathbf {X} _ { A}) = \ int _ {\ mathbf {X} _ {A}} ^ {\ mathbf {X} _ {B}} {\ boldsymbol {\ nabla}} \ mathbf {w} \ cdot d \ mathbf {X } = \ int _ {\ mathbf {X} _ {A}} ^ {\ mathbf {X} _ {B}} ({\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ epsilon}}) \ cdot d \ mathbf {X}}

{\mathbf {w}}({\mathbf {X}}_{B})-{\mathbf {w}}({\mathbf {X}}_{A})=\int _{{{\mathbf {X}}_{A}}}^{{{\mathbf {X}}_{B}}}{\boldsymbol {\nabla }}{\mathbf {w}}\cdot d{\mathbf {X}}=\int _{{{\mathbf {X}}_{A}}}^{{{\mathbf {X}}_{B}}}({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})\cdot d{\mathbf {X}}

Обратите внимание, что нам нужно знать ссылку $w (XA) {\ displaystyle \ mathbf {w} (\ mathbf {X} _ {A})}$ ${\mathbf {w}}({\mathbf {X}}_{A})$ исправить вращение твердого тела. Поле $w (X) {\ displaystyle \ mathbf {w} (\ mathbf {X})}$ ${\mathbf {w}}({\mathbf {X}})$ определяется однозначно, только если контурный интеграл по замкнутому контуру между $XA {\ displaystyle \ mathbf {X} _ {A}}$ ${\mathbf {X}}_{A}$ и $X b {\ displaystyle \ mathbf {X} _ {b}}$ ${\mathbf {X}}_{b}$ равно нулю, т. е.

∮ XAXB (∇ × ϵ) ⋅ d Икс знак равно 0 {\ displaystyle \ oint _ {\ mathbf {X} _ {A}} ^ {\ mathbf {X} _ {B}} ({\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ epsilon}}) \ cdot d \ mathbf {X} = {\ boldsymbol {0}}}

\oint _{{{\mathbf {X}}_{A}}}^{{{\mathbf {X}}_{B}}}({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})\cdot d{\mathbf {X}}={\boldsymbol {0}}

Но из теоремы Стокса для односвязного тела и необходимого условия совместимости

∮ XAXB (∇ × ϵ) ⋅ d X = ∫ Ω AB n ⋅ (∇ × ∇ × ϵ) da = 0 {\ displaystyle \ oint _ {\ mathbf {X} _ {A}} ^ {\ mathbf {X } _ {B}} ({\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ epsilon}}) \ cdot d \ mathbf {X} = \ int _ {\ Omega _ {AB}} \ mathbf {n } \ cdot ({\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ epsilon}}) ~ da = {\ boldsymbol {0}}}

\oint _{{{\mathbf {X}}_{A}}}^{{{\mathbf {X}}_{B}}}({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})\cdot d{\mathbf {X}}=\int _{{\Omega _{{AB}}}}{\mathbf {n}}\cdot ({\boldsymbol {\nabla }}\times {\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})~da={\boldsymbol {0}}

Следовательно, поле $w {\ displaystyle \ mathbf {w}}$ $\mathbf {w}$ i s однозначно определен, что означает, что тензор бесконечно малого вращения $ω {\ displaystyle {\ boldsymbol {\ omega}}}$ ${\boldsymbol {\omega }}$ также однозначно определен, при условии, что тело односвязно.

На следующем этапе процесса мы рассмотрим уникальность поля смещения $u {\ displaystyle \ mathbf {u}}$ $\mathbf {u}$ . Как и раньше, мы интегрируем градиент смещения

u (XB) - u (XA) = ∫ XAXB ∇ u ⋅ d X = ∫ XAXB (ϵ + ω) ⋅ d X {\ displaystyle \ mathbf {u} (\ mathbf { X} _ {B}) - \ mathbf {u} (\ mathbf {X} _ {A}) = \ int _ {\ mathbf {X} _ {A}} ^ {\ mathbf {X} _ {B} } {\ boldsymbol {\ nabla}} \ mathbf {u} \ cdot d \ mathbf {X} = \ int _ {\ mathbf {X} _ {A}} ^ {\ mathbf {X} _ {B}} ( {\ boldsymbol {\ epsilon}} + {\ boldsymbol {\ omega}}) \ cdot d \ mathbf {X}}

{\mathbf {u}}({\mathbf {X}}_{B})-{\mathbf {u}}({\mathbf {X}}_{A})=\int _{{{\mathbf {X}}_{A}}}^{{{\mathbf {X}}_{B}}}{\boldsymbol {\nabla }}{\mathbf {u}}\cdot d{\mathbf {X}}=\int _{{{\mathbf {X}}_{A}}}^{{{\mathbf {X}}_{B}}}({\boldsymbol {\epsilon }}+{\boldsymbol {\omega }})\cdot d{\mathbf {X}}

Из теоремы Стокса и с использованием соотношений $∇ × ϵ = ∇ w = - ∇ × ω {\ displaystyle {\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ epsilon}} = {\ boldsymbol {\ nabla}} \ mathbf {w} = - {\ boldsymbol {\ nabla}} \ times \ omega}$ ${\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }}={\boldsymbol {\nabla }}\mathbf {w} =-{\boldsymbol {\nabla }}\times \omega$ мы имеем

∮ XAXB (ϵ + ω) ⋅ d X = ∫ Ω AB n ⋅ (∇ × ϵ + ∇ × ω) da = 0 {\ displaystyle \ oint _ {\ mathbf {X} _ {A}} ^ {\ mathbf {X} _ {B}} ({\ boldsymbol {\ epsilon}} + {\ boldsymbol {\ omega}}) \ cdot d \ mathbf {X} = \ int _ {\ Omega _ {AB}} \ mathbf {n} \ cdot ({\ boldsymbol {\ nabla}} \ times {\ boldsymbol {\ epsilon}} + {\ boldsymbol {\ nabla}} \ times {\ boldsymbol { \ o mega}}) ~ da = {\ boldsymbol {0}}}

\oint _{{{\mathbf {X}}_{A}}}^{{{\mathbf {X}}_{B}}}({\boldsymbol {\epsilon }}+{\boldsymbol {\omega }})\cdot d{\mathbf {X}}=\int _{{\Omega _{{AB}}}}{\mathbf {n}}\cdot ({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }}+{\boldsymbol {\nabla }}\times {\boldsymbol {\omega }})~da={\boldsymbol {0}}

Следовательно, поле смещения $u {\ displaystyle \ mathbf {u}}$ $\mathbf {u}$ также определяется однозначно. Следовательно, условий совместимости достаточно, чтобы гарантировать существование уникального поля смещения $u {\ displaystyle \ mathbf {u}}$ $\mathbf {u}$ в односвязном теле.

Совместимость для правого поля деформации Коши-Грина

Проблема совместимости для правого поля деформации Коши-Грина может быть поставлена следующим образом.

Задача: Пусть $C (X) {\ displaystyle {\ boldsymbol {C}} (\ mathbf {X})}$ ${\boldsymbol {C}}({\mathbf {X}})$ будет положительно определенным симметричным тензорным полем, определенным на эталонная конфигурация. При каких условиях на $C {\ displaystyle {\ boldsymbol {C}}}$ ${\boldsymbol {C}}$ существует деформированная конфигурация, отмеченная полем положения $x (X) {\ displaystyle \ mathbf {x } (\ mathbf {X})}$ ${\mathbf {x}}({\mathbf {X}})$ такой, что

(1) (∂ x ∂ X) T (∂ x ∂ X) = C {\ displaystyle (1) \ quad \ left ({ \ frac {\ partial \ mathbf {x}} {\ partial \ mathbf {X}}} \ right) ^ {T} \ left ({\ frac {\ partial \ mathbf {x}} {\ partial \ mathbf {X }}} \ right) = {\ boldsymbol {C}}}

(1)\quad \left({\frac {\partial {\mathbf {x}}}{\partial {\mathbf {X}}}}\right)^{T}\left({\frac {\partial {\mathbf {x}}}{\partial {\mathbf {X}}}}\right)={\boldsymbol {C}}

Необходимые условия

Предположим, что поле $x (X) {\ displaystyle \ mathbf {x} (\ mathbf {X })}$ ${\mathbf {x}}({\mathbf {X}})$ существует, удовлетворяющее условию (1). В терминах компонентов относительно прямоугольного декартова базиса

∂ xi ∂ X α ∂ xi ∂ X β = C α β {\ displaystyle {\ frac {\ partial x ^ {i}} {\ partial X ^ {\ alpha}}} {\ frac {\ partial x ^ {i}} {\ partial X ^ {\ beta}}} = C _ {\ alpha \ beta}}

{\frac {\partial x^{i}}{\partial X^{\alpha }}}{\frac {\partial x^{i}}{\partial X^{\beta }}}=C_{{\alpha \beta }}

Из теории конечных деформаций мы знайте, что $C α β = g α β {\ displaystyle C _ {\ alpha \ beta} = g _ {\ alpha \ beta}}$ $C_{{\alpha \beta }}=g_{{\alpha \beta }}$ . Следовательно, мы можем написать

δ ij ∂ xi ∂ X α ∂ xj ∂ X β = g α β {\ displaystyle \ delta _ {ij} ~ {\ frac {\ partial x ^ {i}} {\ partial X ^ {\ alpha}}} ~ {\ frac {\ partial x ^ {j}} {\ partial X ^ {\ beta}}} = g _ {\ alpha \ beta}}

\delta _{{ij}}~{\frac {\partial x^{i}}{\partial X^{\alpha }}}~{\frac {\partial x^{j}}{\partial X^{\beta }}}=g_{{\alpha \beta }}

Для двух симметричных тензорных полей второго порядка которые отображаются взаимно однозначно, мы также имеем отношение

G ij = ∂ X α ∂ xi ∂ X β ∂ xjg α β {\ displaystyle G_ {ij} = {\ frac {\ partial X ^ {\ alpha}} {\ partial x ^ {i}}} ~ {\ frac {\ partial X ^ {\ beta}} {\ partial x ^ {j}}} ~ g _ {\ alpha \ beta}}

G_{{ij}}={\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}~g_{{\alpha \beta }}

Из отношения между $G ij {\ displaystyle G_ {ij}}$ $G_{{ij}}$ и $g α β {\ displaystyle g _ {\ alpha \ beta}}$ $g_{\alpha\beta}$ , что $δ ij = G ij {\ displaystyle \ delta _ {ij} = G_ {ij}}$ $\delta _{{ij}}=G_{{ij}}$ , мы имеем

(x) Γ ijk = 0 {\ displaystyle _ {(x) } \ Gamma _ {ij} ^ {k} = 0}

_{{(x)}}\Gamma _{{ij}}^{k}=0

Тогда из соотношения

∂ 2 xm ∂ X α ∂ X β = ∂ xm ∂ X μ (X) Γ α β μ - ∂ xi ∂ Икс α ∂ xj ∂ Икс β (x) Γ ijm {\ displaystyle {\ frac {\ partial ^ {2} x ^ {m}} {\ partial X ^ {\ alpha} \ partial X ^ {\ beta}} } = {\ frac {\ partial x ^ {m}} {\ pa rtial X ^ {\ mu}}} \, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ mu} - {\ frac {\ partial x ^ {i}} {\ partial X ^ { \ alpha}}} ~ {\ frac {\ partial x ^ {j}} {\ partial X ^ {\ beta}}} \, _ {(x)} \ Gamma _ {ij} ^ {m}}

{\frac {\partial ^{2}x^{m}}{\partial X^{\alpha }\partial X^{\beta }}}={\frac {\partial x^{m}}{\partial X^{\mu }}}\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }-{\frac {\partial x^{i}}{\partial X^{\alpha }}}~{\frac {\partial x^{j}}{\partial X^{\beta }}}\,_{{(x)}}\Gamma _{{ij}}^{m}

имеем

∂ F α m ∂ X β = F μ m (X) Γ α β μ; F α я: знак равно ∂ xi ∂ Икс α {\ displaystyle {\ frac {\ partial F_ {~ \ alpha} ^ {m}} {\ partial X ^ {\ beta}}} = F_ {~ \ mu} ^ { m} \, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ mu} \ qquad; ~~ F_ {~ \ alpha} ^ {i}: = {\ frac {\ partial x ^ { i}} {\ partial X ^ {\ alpha}}}}

{\frac {\partial F_{{~\alpha }}^{m}}{\partial X^{\beta }}}=F_{{~\mu }}^{m}\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }\qquad ;~~F_{{~\alpha }}^{i}:={\frac {\partial x^{i}}{\partial X^{\alpha }}}

Из теории конечных деформаций мы также имеем

(X) Γ α β γ = 1 2 (∂ g α γ ∂ X β + ∂ g β γ ∂ X α - ∂ g α β ∂ X γ); (X) Γ α β ν = g ν γ (X) Γ α β γ; g α β = C α β; g α β знак равно C α β {\ Displaystyle _ {(X)} \ Gamma _ {\ alpha \ beta \ gamma} = {\ frac {1} {2}} \ left ({\ frac {\ partial g _ {\ alpha \ gamma}} {\ partial X ^ {\ beta}}} + {\ frac {\ partial g _ {\ beta \ gamma}} {\ partial X ^ {\ alpha}}} - {\ frac {\ partial g_ {\ alpha \ beta}} {\ partial X ^ {\ gamma}}} \ right) ~; ~~ _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ nu} = g ^ {\ nu \ gamma} \, _ {(X)} \ Gamma _ {\ alpha \ beta \ gamma} ~; ~~ g _ {\ alpha \ beta} = C _ {\ alpha \ beta} ~; ~~ g ^ {\ alpha \ beta} = C ^ {\ alpha \ beta}}

_{{(X)}}\Gamma _{{\alpha \beta \gamma }}={\frac {1}{2}}\left({\frac {\partial g_{{\alpha \gamma }}}{\partial X^{\beta }}}+{\frac {\partial g_{{\beta \gamma }}}{\partial X^{\alpha }}}-{\frac {\partial g_{{\alpha \beta }}}{\partial X^{\gamma }}}\right)~;~~_{{(X)}}\Gamma _{{\alpha \beta }}^{\nu }=g^{{\nu \gamma }}\,_{{(X)}}\Gamma _{{\alpha \beta \gamma }}~;~~g_{{\alpha \beta }}=C_{{\alpha \beta }}~;~~g^{{\alpha \beta }}=C^{{\alpha \beta }}

Следовательно,

(X) Γ α β μ = C μ γ 2 (∂ C α γ ∂ X β + ∂ C β γ ∂ X α - ∂ С α β ∂ Икс γ) {\ Displaystyle \, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ mu} = {\ cfrac {C ^ {\ mu \ gamma}} {2 }} \ left ({\ frac {\ partial C _ {\ alpha \ gamma}} {\ partial X ^ {\ beta}}} + {\ frac {\ partial C _ {\ beta \ gamma}} {\ partial X ^ {\ alpha}}} - {\ frac {\ partial C _ {\ alpha \ beta}} {\ partial X ^ {\ gamma}}} \ right)}

\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }={\cfrac {C^{{\mu \gamma }}}{2}}\left({\frac {\partial C_{{\alpha \gamma }}}{\partial X^{\beta }}}+{\frac {\partial C_{{\beta \gamma }}}{\partial X^{\alpha }}}-{\frac {\partial C_{{\alpha \beta }}}{\partial X^{\gamma }}}\right)

и мы имеем

∂ F α m ∂ Икс β знак равно F μ м С μ γ 2 (∂ C α γ ∂ X β + ∂ C β γ ∂ X α - ∂ C α β ∂ X γ) {\ displaystyle {\ frac {\ partial F_ {~ \ alpha} ^ {m}} {\ partial X ^ {\ beta}}} = F_ {~ \ mu} ^ {m} ~ {\ cfrac {C ^ {\ mu \ gamma}} {2}} \ left ({\ frac {\ partial C _ {\ alpha \ gamma}} {\ partial X ^ {\ beta}}} + {\ frac { \ partial C _ {\ beta \ gamma}} {\ partial X ^ {\ alpha}}} - {\ frac {\ partial C _ {\ alpha \ beta}} {\ partial X ^ {\ gamma}}} \ right) }

{\frac {\partial F_{{~\alpha }}^{m}}{\partial X^{\beta }}}=F_{{~\mu }}^{m}~{\cfrac {C^{{\mu \gamma }}}{2}}\left({\frac {\partial C_{{\alpha \gamma }}}{\partial X^{\beta }}}+{\frac {\partial C_{{\beta \gamma }}}{\partial X^{\alpha }}}-{\frac {\partial C_{{\alpha \beta }}}{\partial X^{\gamma }}}\right)

Опять же, используя коммутативный характер порядка дифференцирования, мы имеем

∂ 2 F α m ∂ X β ∂ X ρ = ∂ 2 F α m ∂ X ρ ∂ X β ⟹ ∂ F μ m ∂ X ρ (X) Γ α β μ + F μ m ∂ ∂ X ρ [(X) Γ α β μ] = ∂ F μ m ∂ X β (X) Γ α ρ μ + F μ m ∂ ∂ X β [ (X) Γ α ρ μ] {\ Displaystyle {\ frac {\ partial ^ {2} F_ {~ \ alpha} ^ {m}} {\ partial X ^ {\ beta} \ partial X ^ {\ rho}} } = {\ frac {\ partial ^ {2} F_ {~ \ alpha} ^ {m}} {\ partial X ^ {\ rho} \ partial X ^ {\ beta}}} \ подразумевает {\ frac {\ partial F_ {~ \ mu} ^ {m}} {\ partial X ^ {\ rho}}} \, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ mu} + F_ {~ \ mu } ^ {m} ~ {\ frac {\ partial} {\ partial X ^ {\ rho}}} [\, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ mu}] = { \ frac {\ partial F_ {~ \ mu} ^ {m}} {\ partial X ^ {\ beta}}} \, _ {(X)} \ Gamma _ {\ alpha \ rho} ^ {\ mu} + F_ {~ \ mu} ^ {m} ~ {\ frac {\ partial} {\ partial X ^ {\ beta}}} [\, _ {(X) } \ Gamma _ {\ alpha \ rho} ^ {\ mu}]}

{\frac {\partial ^{2}F_{{~\alpha }}^{m}}{\partial X^{\beta }\partial X^{\rho }}}={\frac {\partial ^{2}F_{{~\alpha }}^{m}}{\partial X^{\rho }\partial X^{\beta }}}\implies {\frac {\partial F_{{~\mu }}^{m}}{\partial X^{\rho }}}\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }+F_{{~\mu }}^{m}~{\frac {\partial }{\partial X^{\rho }}}[\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }]={\frac {\partial F_{{~\mu }}^{m}}{\partial X^{\beta }}}\,_{{(X)}}\Gamma _{{\alpha \rho }}^{\mu }+F_{{~\mu }}^{m}~{\frac {\partial }{\partial X^{\beta }}}[\,_{{(X)}}\Gamma _{{\alpha \rho }}^{\mu }]

или

F γ m (X) Γ μ ρ γ (X) Γ α β μ + F μ m ∂ ∂ X ρ [ (Икс) Γ α β μ] знак равно F γ м (Икс) Γ μ β γ (X) Γ α ρ μ + F μ м ∂ ∂ X β [(X) Γ α ρ μ] {\ Displaystyle F_ {~ \ gamma} ^ {m} \, _ {(X)} \ Gamma _ {\ mu \ rho} ^ {\ gamma} \, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ mu} + F_ {~ \ mu} ^ {m} ~ {\ frac {\ partial} {\ partial X ^ {\ rho}}} [\, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ { \ mu}] = F_ {~ \ gamma} ^ {m} \, _ {(X)} \ Gamma _ {\ mu \ beta} ^ {\ gamma} \, _ {(X)} \ Gamma _ {\ альфа \ rho} ^ {\ mu} + F_ {~ \ mu} ^ {m} ~ {\ frac {\ partial} {\ partial X ^ {\ beta}}} [\, _ {(X)} \ Gamma _ {\ alpha \ rho} ^ {\ mu}]}

F_{{~\gamma }}^{m}\,_{{(X)}}\Gamma _{{\mu \rho }}^{\gamma }\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }+F_{{~\mu }}^{m}~{\frac {\partial }{\partial X^{\rho }}}[\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }]=F_{{~\gamma }}^{m}\,_{{(X)}}\Gamma _{{\mu \beta }}^{\gamma }\,_{{(X)}}\Gamma _{{\alpha \rho }}^{\mu }+F_{{~\mu }}^{m}~{\frac {\partial }{\partial X^{\beta }}}[\,_{{(X)}}\Gamma _{{\alpha \rho }}^{\mu }]

Собрав члены, мы получаем

F γ m ((X) Γ μ ρ γ (X) Γ α β μ + ∂ ∂ X ρ [( Икс) Γ α β γ] - (X) Γ μ β γ (X) Γ α ρ μ - ∂ ∂ X β [(X) Γ α ρ γ]) = 0 {\ displaystyle F_ {~ \ gamma} ^ { m} \ left (\, _ {(X)} \ Gamma _ {\ mu \ rho} ^ {\ gamma} \, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ mu} + {\ frac {\ partial} {\ partial X ^ {\ rho}}} [\, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ gamma}] - \, _ {(X) } \ Gamma _ {\ mu \ beta} ^ {\ gamma} \, _ {(X)} \ Gamma _ {\ alpha \ r ho} ^ {\ mu} - {\ frac {\ partial} {\ partial X ^ {\ beta}}} [\, _ {(X)} \ Gamma _ {\ alpha \ rho} ^ {\ gamma}] \ right) = 0}

F_{{~\gamma }}^{m}\left(\,_{{(X)}}\Gamma _{{\mu \rho }}^{\gamma }\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }+{\frac {\partial }{\partial X^{\rho }}}[\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\gamma }]-\,_{{(X)}}\Gamma _{{\mu \beta }}^{\gamma }\,_{{(X)}}\Gamma _{{\alpha \rho }}^{\mu }-{\frac {\partial }{\partial X^{\beta }}}[\,_{{(X)}}\Gamma _{{\alpha \rho }}^{\gamma }]\right)=0

Из определения $F γ m {\ displaystyle F _ {\ gamma} ^ {m}}$ $F_{{\gamma }}^{m}$ мы видим, что он обратим и, следовательно, не может быть нулевым. Следовательно,

R α β ρ γ: = ∂ ∂ X ρ [(X) Γ α β γ] - ∂ ∂ X β [(X) Γ α ρ γ] + (X) Γ μ ρ γ (X) Γ α β μ - (Икс) Γ μ β γ (X) Γ α ρ μ знак равно 0 {\ displaystyle R _ {\ alpha \ beta \ rho} ^ {\ gamma}: = {\ frac {\ partial} {\ partial X ^ {\ rho}}} [\, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ gamma}] - {\ frac {\ partial} {\ partial X ^ {\ beta}} } [\, _ {(X)} \ Gamma _ {\ alpha \ rho} ^ {\ gamma}] + \, _ {(X)} \ Gamma _ {\ mu \ rho} ^ {\ gamma} \, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ mu} - \, _ {(X)} \ Gamma _ {\ mu \ beta} ^ {\ gamma} \, _ {(X) } \ Gamma _ {\ alpha \ rho} ^ {\ mu} = 0}

R_{{\alpha \beta \rho }}^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\,_{{(X)}}\Gamma _{{\alpha \rho }}^{\gamma }]+\,_{{(X)}}\Gamma _{{\mu \rho }}^{\gamma }\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }-\,_{{(X)}}\Gamma _{{\mu \beta }}^{\gamma }\,_{{(X)}}\Gamma _{{\alpha \rho }}^{\mu }=0

Мы можем показать, что это смешанные компоненты тензора кривизны Римана-Кристоффеля. Следовательно, необходимые условия для $C {\ displaystyle {\ boldsymbol {C}}}$ ${\boldsymbol {C}}$ -совместимости заключаются в том, что кривизна деформации по Риману-Кристоффелю равна нулю.

Достаточные условия

Доказательство достаточности немного сложнее. Начнем с предположения, что

R α β ρ γ = 0; g α β знак равно C α β {\ Displaystyle R _ {\ alpha \ beta \ rho} ^ {\ gamma} = 0 ~; ~~ g _ {\ alpha \ beta} = C _ {\ alpha \ beta}}

R_{{\alpha \beta \rho }}^{\gamma }=0~;~~g_{{\alpha \beta }}=C_{{\alpha \beta }}

Мы должны показать, что существуют $x {\ displaystyle \ mathbf {x}}$ $\mathbf {x}$ и $X {\ displaystyle \ mathbf {X}}$ $\mathbf {X}$ такие, что

∂ xi ∂ X α ∂ xi ∂ X β знак равно C α β {\ displaystyle {\ frac {\ partial x ^ {i}} {\ partial X ^ {\ alpha}}} {\ frac {\ partial x ^ {i }} {\ partial X ^ {\ beta}}} = C _ {\ alpha \ beta}}

{\frac {\partial x^{i}}{\partial X^{\alpha }}}{\frac {\partial x^{i}}{\partial X^{\beta }}}=C_{{\alpha \beta }}

Из теоремы Т.Ю. Томаса мы знаем, что система уравнений

∂ F α i ∂ X β = F γ я (Икс) Γ α β γ {\ Displaystyle {\ frac {\ partial F_ {~ \ alpha} ^ {i}} {\ partial X ^ {\ beta}}} = F_ {~ \ gamma} ^ {я } ~ \, _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ gamma}}

{\frac {\partial F_{{~\alpha }}^{i}}{\partial X^{\bet a }}}=F_{{~\gamma }}^{i}~\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\gamma }

имеет уникальные решения $F α i {\ displaystyle F_ {~ \ alpha} ^ {i} }$ $F_{{~\alpha }}^{i}$ над односвязными областями, если

(X) Γ α β γ = (X) Γ β α γ; Р α β ρ γ знак равно 0 {\ Displaystyle _ {(X)} \ Gamma _ {\ alpha \ beta} ^ {\ gamma} = _ {(X)} \ Gamma _ {\ beta \ alpha} ^ {\ gamma } ~; ~~ R _ {\ alpha \ beta \ rho} ^ {\ gamma} = 0}

_{{(X)}}\Gamma _{{\alpha \beta }}^{\gamma }=_{{(X)}}\Gamma _{{\beta \alpha }}^{\gamma }~;~~R_{{\alpha \beta \rho }}^{\gamma }=0

Первое из них верно из определения $Γ jki {\ displaystyle \ Gamma _ {jk} ^ {i}}$ $\Gamma _{{jk}}^{i}$ , и предполагается второе. Следовательно, предполагаемое условие дает нам уникальный $F α i {\ displaystyle F_ {~ \ alpha} ^ {i}}$ $F_{{~\alpha }}^{i}$ , то есть $C 2 {\ displaystyle C ^ {2}}$ $C^{2}$ непрерывно.

Затем рассмотрим систему уравнений

∂ xi ∂ X α = F α i {\ displaystyle {\ frac {\ partial x ^ {i}} {\ partial X ^ {\ alpha}}} = F_ {~ \ alpha} ^ {i}}

{\frac {\partial x^{i}}{\partial X^{\alpha }}}=F_{{~\alpha }}^{i}

Поскольку $F α i {\ displaystyle F_ {~ \ alpha} ^ {i}}$ $F_{{~\alpha }}^{i}$ равно $C 2 {\ displaystyle C ^ {2}}$ $C^{2}$ и тело односвязно, существует некоторое решение $xi (X α) {\ displaystyle x ^ {i} (X ^ {\ alpha})}$ $x^{i}(X^{\alpha })$ к приведенным выше уравнениям. Мы можем показать, что $x i {\ displaystyle x ^ {i}}$ $x^{i}$ также удовлетворяет свойству

det | ∂ x i ∂ X α | ≠ 0 {\ displaystyle \ det \ left | {\ frac {\ partial x ^ {i}} {\ partial X ^ {\ alpha}}} \ right | \ neq 0}

\det \left|{\frac {\partial x^{i}}{\partial X^{\alpha }}}\right|\neq 0

Мы также можем показать, что отношение

∂ xi ∂ X α g α β ∂ xj ∂ X β = δ ij {\ displaystyle {\ frac {\ partial x ^ {i}} {\ partial X ^ {\ alpha}}} ~ g ^ {\ alpha \ beta} ~ {\ frac {\ partial x ^ {j}} {\ partial X ^ {\ beta}}} = \ delta ^ {ij}}

{\frac {\partial x^{i}}{\partial X^{\alpha }}}~g^{{\alpha \beta }}~{\frac {\partial x^{j}}{\partial X^{\beta }}}=\delta ^{{ij}}

означает, что

g α β = C α β знак равно ∂ xk ∂ X α ∂ xk ∂ X β {\ displaystyle g _ {\ alpha \ beta} = C _ {\ alpha \ beta} = {\ frac {\ partial x ^ {k}} {\ partial X ^ {\ alpha}}} ~ {\ frac {\ partial x ^ {k}} {\ partial X ^ {\ beta}}}}

g_{{\alpha \beta }}=C_{{\alpha \beta }}={\frac {\partial x^{k}}{\partial X^{\alpha }}}~{\frac {\partial x^{k}}{\partial X^{\beta }}}

Если мы свяжем эти величины с тензорными полями, мы можем показать, что $∂ x ∂ X {\ displaystyle {\ frac {\ partial \ mathbf {x}} {\ partial \ mathbf {X}}}}$ ${\frac {\partial {\mathbf {x}}}{\partial {\mathbf {X}}}}$ обратимо, и построенное тензорное поле удовлетворяет выражению для $C {\ displaystyle {\ boldsymbol {C}}}$ ${\boldsymbol {C}}$ .

См. также

Ссылки

^C. Amrouche, PG Ciarlet, L Gratie, S. Kesavan, On the Saint Venant's совместимость и лемма Пуанкаре, C.R. Acad. Sci. Париж, сер. I, 342 (2006), 887-891. doi : 10.1016 / j.crma.2006.03.026
^Барбер, Дж. Р., 2002, Эластичность - 2-е изд., Kluwer Academic Publications.
^Н.И. Мусхелишвили, Некоторые основные проблемы математической теории упругости. Лейден: Noordhoff Intern. Publ., 1975.
^Slaughter, W. S., 2003, The linearized theory of elasticity, Birkhauser
^ Acharya, A., 1999, On Compatibility Conditions for the Left Cauchy–Green Deformation Field in Three Dimensions, Journal of Elasticity, Volume 56, Number 2, 95-105
^Blume, J. A., 1989, "Compatibility conditions for a left Cauchy-Green strain field", J. Elasticity, v. 21, p. 271-308.
^Thomas, T. Y., 1934, "Systems of total differential equations defined over simply connected domains", Annals of Mathematics, 35(4), p. 930-734

External links