Тождество Бельтрами

редактировать

Частный случай уравнений Эйлера-Лагранжа

Эудженио Бельтрами

Тождество Бельтрами, названное в честь Эухенио Бельтрами, является частным случаем уравнения Эйлера – Лагранжа в исчислении v ariations.

Уравнение Эйлера – Лагранжа служит для экстремума действия функционалов вида

I [u] = ∫ ab L [x, u (x), u ′ (x)] dx, {\ displaystyle I [u] = \ int _ {a} ^ {b} L [x, u (x), u '(x)] \, dx \,,}

I[u]=\int_a^b L[x,u(x),u'(x)] \, dx \,,

где $a {\ displaystyle a}$ $a$ и $b {\ displaystyle b}$ $b$ являются константами, а $u ′ (x) = dudx {\ displaystyle u '(x) = {\ frac {du} {dx}}}$ $u'(x)={\frac {du}{dx}}$ .

Если $∂ L ∂ x = 0 {\ displaystyle {\ frac {\ partial L} {\ partial x}} = 0}$ ${\ displaystyle {\ frac {\ partial L} {\ partial x}} = 0}$ , то Уравнение Эйлера – Лагранжа сводится к тождеству Бельтрами,

$L - u ′ ∂ L ∂ u ′ = C, {\ displaystyle L-u '{\ frac {\ partial L} {\ partial u'}} = C \,,}$ $L-u'{\frac {\partial L}{\partial u'}}=C\,,$

где C - константа.

Содержание

1 Выведение
2 Приложения
- 2.1 Решение проблемы брахистохрона
3 Примечания
4 Ссылки

Выведение

Следующий вывод тождества Бельтрами начинается с уравнения Эйлера – Лагранжа,

∂ L ∂ u = ddx ∂ L ∂ u ′. {\ displaystyle {\ frac {\ partial L} {\ partial u}} = {\ frac {d} {dx}} {\ frac {\ partial L} {\ partial u '}} \,.}

{\frac {\partial L}{\partial u}}={\frac {d}{dx}}{\frac {\partial L}{\partial u'}}\,.

Умножая обе части на u ′,

u ′ ∂ L ∂ u = u ′ ddx ∂ L ∂ u ′. {\ displaystyle u '{\ frac {\ partial L} {\ partial u}} = u' {\ frac {d} {dx}} {\ frac {\ partial L} {\ partial u '}} \,. }

u'{\frac {\partial L}{\partial u}}=u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}\,.

Согласно правилу цепочки ,

d L dx = ∂ L ∂ uu ′ + ∂ L ∂ u ′ u ″ + ∂ L ∂ x, {\ displaystyle {dL \ over dx} = {\ частичное L \ over \ partial u} u '+ {\ partial L \ over \ partial u'} u '' + {\ partial L \ over \ partial x} \,,}

{dL \over dx}={\partial L \over \partial u}u'+{\partial L \over \partial u'}u''+{\partial L \over \partial x}\,,

где $u ″ = du ′ dx = d 2 udx 2 {\ displaystyle u '' = {\ frac {du '} {dx}} = {\ frac {d ^ {2} u} {dx ^ {2}}}}$ $u''={\frac {du'}{dx}}={\frac {d^{2}u}{dx^{2}}}$ .

Перестановка этого дает

u ′ ∂ L ∂ u = d L dx - ∂ L ∂ u ′ u ″ - ∂ L ∂ x. {\ displaystyle u '{\ partial L \ over \ partial u} = {dL \ over dx} - {\ partial L \ over \ partial u'} u '' - {\ partial L \ over \ partial x} \,.}

u'{\partial L \over \partial u}={dL \over dx}-{\partial L \over \partial u'}u''-{\partial L \over \partial x}\,.

Таким образом, подставляя это выражение для $u ′ ∂ L ∂ u {\ displaystyle u '{\ frac {\ partial L} {\ partial u}}}$ $u'{\frac {\partial L}{\partial u}}$ во второе уравнение этого вывода

d L dx - ∂ L ∂ u ′ u ″ - ∂ L ∂ x - u ′ ddx ∂ L ∂ u ′ = 0. {\ displaystyle {dL \ over dx} - {\ partial L \ over \ partial u '} u' '- {\ partial L \ over \ partial x} -u' {\ frac {d} {dx}} {\ frac {\ partial L} {\ partial u '}} = 0 \,.}

{dL \over dx}-{\partial L \over \partial u'}u''-{\partial L \over \partial x}-u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}=0\,.

По правилу произведения последний член повторно выражается как

u ′ ddx ∂ L ∂ u ′ = ddx (∂ L ∂ u ′ u ′) - ∂ L ∂ u ′ u ″, {\ displaystyle u '{\ frac {d} {dx}} {\ frac {\ partial L} {\ partial u'}} = {\ frac {d} {dx}} \ left ({\ frac {\ partial L} {\ partial u '}} u' \ right) - {\ frac {\ partial L} {\ partial u '}} u' '\,,}

u'\frac{d}{dx}\frac{\partial L}{\partial u'}=\frac{d}{dx}\left( \frac{\partial L}{\partial u'}u' \right)-\frac{\partial L}{\partial u'}u'' \,

и переставляя,

ddx (L - u ′ ∂ L ∂ u ′) = ∂ L ∂ x. {\ displaystyle {d \ over dx} \ left ({L-u '{\ frac {\ partial L} {\ partial u'}}} \ right) = {\ partial L \ over \ partial x} \,. }

{d \over dx}\left({L-u'{\frac {\partial L}{\partial u'}}}\right)={\partial L \over \partial x}\,.

В случае $∂ L ∂ x = 0 {\ displaystyle {\ frac {\ partial L} {\ partial x}} = 0}$ ${\ displaystyle {\ frac {\ partial L} {\ partial x}} = 0}$ это сокращается до

ddx (L - и '∂ L ∂ u') знак равно 0, {\ displaystyle {d \ over dx} \ left ({L-u '{\ frac {\ partial L} {\ partial u'}}} \ right) = 0 \,,}

{d \over dx}\left({L-u'{\frac {\partial L}{\partial u'}}}\right)=0\,,

, так что взятие первообразной приводит к тождеству Бельтрами,

L - u ′ ∂ L ∂ u ′ = C, {\ displaystyle L-u '{ \ frac {\ partial L} {\ partial u '}} = C \,,}

L-u'{\frac {\partial L}{\partial u'}}=C\,,

где C - константа.

Приложения

Решение проблемы брахистохрона

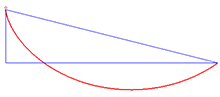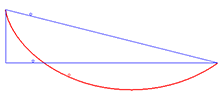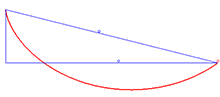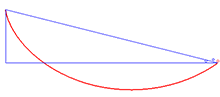
Решением проблемы брахистохрона является циклоида.

Примером применения тождества Бельтрами является проблема брахистохрона, которая включает в себя поиск кривой $y = y (x) {\ displaystyle y = y (x)}$ ${\ displaystyle y = y (x)}$ , который минимизирует интеграл

I [y] = ∫ 0 a 1 + y ′ 2 ydx. {\ displaystyle I [y] = \ int _ {0} ^ {a} {\ sqrt {{1 + y '^ {\, 2}} \ over y}} dx \,.}

I[y] = \int_0^a \sqrt { {1+y'^{\, 2}} \over y } dx \,.

Подынтегральное выражение

L (y, y ′) = 1 + y ′ 2 y {\ displaystyle L (y, y ') = {\ sqrt {{1 + y' ^ {\, 2}} \ over y}}}

L(y,y') = \sqrt{ {1+y'^{\, 2}} \over y }

явно не зависит от переменной интегрирования $x {\ displaystyle x}$ $x$ , поэтому применяется тождество Бельтрами,

L - y ′ ∂ L ∂ y ′ = C. {\ displaystyle L-y '{\ frac {\ partial L} {\ partial y'}} = C \,.}

L-y'{\frac {\partial L}{\partial y'}}=C\,.

Замена на $L {\ displaystyle L}$ $L$ и упрощение

y (1 + y ′ 2) = 1 / C 2 (константа), {\ displaystyle y (1 + y '^ {\, 2}) = 1 / C ^ {2} ~~ {\ text {(константа)}} \,,}

y(1+y'^{\, 2}) = 1/C^2 ~~\text {(constant)} \,

, которая может быть решена в виде параметрических уравнений

x = A (ϕ - sin ⁡ ϕ) {\ displaystyle x = A ( \ phi - \ sin \ phi)}

x = A (\ phi - \ sin \ phi)

y = A (1 - cos ⁡ ϕ) {\ displaystyle y = A (1- \ cos \ phi)}

y = A (1 - \ cos \ phi)

с $A {\ displaystyle A}$ $A$ равняется половине указанной выше константы, $1 2 C 2 {\ displaystyle {\ frac {1} {2C ^ {2}}}}$ ${\ displaystyle {\ frac {1} {2C ^ {2 }}}}$ и $ϕ { \ displaystyle \ phi}$ $\ phi$ - переменная. Это параметрические уравнения для циклоиды.

Примечания

^Таким образом, преобразование Лежандра лагранжиана , гамильтониан, является постоянным по динамичному пути.

Ссылки