Единая норма

редактировать

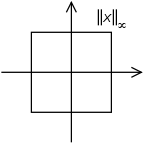
Периметр квадрата - это набор точек в R, где sup norm равен фиксированной положительной константе.

В математическом анализе единообразная норма (или sup norm ) присваивается вещественному- или комплексному -значные ограниченные функции f, определенные на множестве S неотрицательное число

‖ f ‖ ∞ = ‖ f ‖ ∞, S = sup {| f (x) | : x ∈ S}. {\ Displaystyle \ | е \ | _ {\ infty} = \ | е \ | _ {\ infty, S} = \ sup \ left \ {\, \ left | f (x) \ right |: x \ in S \, \ right \}.}

\ | f \ | _ {\ infty} = \ | f \ | _ {\ infty, S} = \ sup \ left \ {\, \ left | f (x) \ right |: x \ in S \, \ right \}.

Эта норма также называется нормой супремума, нормой Чебышева, нормой бесконечности, или, когда супремум фактически является максимумом, максимальной нормой . Название «единая норма» происходит от того факта, что последовательность функций ${fn} {\ displaystyle \ {f_ {n} \}}$ $\ {f_ {n} \}$ сходится к $f {\ displaystyle f}$ $f$ в соответствии с метрикой, полученной из единой нормы тогда и только тогда, когда $fn {\ displaystyle f_ {n}}$ $f_ {n}$ сходится к $f {\ displaystyle f}$ $f$ равномерно.

Метрика, порождаемая этой нормой, называется метрикой Чебышева, в честь Пафнутия Чебышева, который первым ее систематически изучил.

Если мы допускаем неограниченные функции, эта формула не дает норму или метрику в строгом смысле, хотя полученная так называемая расширенная метрика все же позволяет определить топологию на функции рассматриваемое пространство.

Если f является непрерывной функцией на закрытом интервале или, в более общем смысле, компактным множеством, то она ограничена и супремум в приведенном выше определении достигается с помощью теоремы Вейерштрасса об экстремальных значениях, поэтому мы можем заменить верхнюю грань на максимум. В этом случае норма также называется максимальной нормой . В частности, в случае вектора $x = (x 1,…, xn) {\ displaystyle x = (x_ {1}, \ dots, x_ {n})}$ $x = (x_ {1}, \ dots, x_ {n})$ in конечное мерное координатное пространство, оно принимает вид

‖ x ‖ ∞ = max {| х 1 |,…, | х п | }. {\ displaystyle \ | x \ | _ {\ infty} = \ max \ {| x_ {1} |, \ dots, | x_ {n} | \}.}

\ | x \ | _ {\ infty} = \ max \ {| x_ {1} |, \ dots, | x_ {n} | \}.

Причина для нижнего индекса «∞» - что всякий раз, когда f непрерывно

lim p → ∞ ‖ f ‖ p = ‖ f ‖ ∞, {\ displaystyle \ lim _ {p \ rightarrow \ infty} \ | f \ | _ {p} = \ | f \ | _ {\ infty},}

\ lim _ {p \ rightarrow \ infty} \ | f \ | _ {p} = \ | f \ | _ {\ infty},

где

‖ е ‖ p = (∫ D | f | pd μ) 1 / p {\ displaystyle \ | f \ | _ {p} = \ left (\ int _ {D} \ left | f \ right | ^ {p} \, d \ mu \ right) ^ {1 / p}}

\ | f \ | _ {p} = \ left (\ int _ {D} \ left | f \ right | ^ {p} \, d \ mu \ right) ^ {1 / p}

где D - область определения f (а интеграл равен сумме, если D равен a дискретный набор ).

Двоичная функция

d (f, g) = ‖ f - g ‖ ∞ {\ displaystyle d (f, g) = \ | fg \ | _ {\ infty}}

d (f, g) = \ | fg \ | _ {\ infty}

тогда метрика на пространстве всех ограниченных функций (и, очевидно, любого из ее подмножеств) в определенной области. Последовательность {f n : n = 1, 2, 3,...} равномерно сходится к функции f тогда и только тогда, когда

lim n → ∞ ‖ fn - е ‖ ∞ = 0. {\ displaystyle \ lim _ {n \ rightarrow \ infty} \ | f_ {n} -f \ | _ {\ infty} = 0. \,}

\ lim _ {n \ rightarrow \ infty} \ | f_ {n} -f \ | _ {\ infty} = 0. \,

Мы можем определять замкнутые множества и замыкания множеств относительно этой метрической топологии; замкнутые множества в равномерной норме иногда называют равномерно замкнутыми и замыкающие равномерные замыкания. Равномерное замыкание набора функций A - это пространство всех функций, которые могут быть аппроксимированы последовательностью равномерно сходящихся функций на A. Например, одно из повторений теоремы Стоуна – Вейерштрасса состоит в том, что набор всех непрерывных функций на $[a, b] {\ displaystyle [a, b]}$ $[a, b]$ - это равномерное замыкание набора многочленов на $[a, b] {\ displaystyle [a, b]}$ $[a, b]$ .

Для сложных непрерывных функций над компактным пространством это превращает его в алгебру C *.

См. также

Литература