Солитон (оптика)

В оптике термин солитон используется для обозначения любого оптическое поле, которое не изменяется во время распространения из-за тонкого баланса между нелинейными и линейными эффектами в среде. Существует два основных типа солитонов:

• пространственные солитоны : нелинейный эффект может уравновесить дифракцию. Электромагнитное поле может проб показатель преломления среды при распространении, создаваемом таким образом распространенной, волокну с градиентным коэффициентом преломления.
• временные солитоны : если поле уже пространственно ограничено, то оно останется ограниченным и будет изменяться без изменений своей формы
• временные солитоны : эффекты уравновешивают дисперсию. Эти солитоны были открыты первыми, и в оптике их часто называют просто «солитонами».

• 1 Пространственные солитоны
  • 1.1 Доказательство
  • 1.2 Генерация пространственных солитонов
  • 1.3 Поперечная синхронизация мод солитонов
• 2 Временные солитоны
  • 2.1 История временных солитонов
  • 2.2 Доказательство для временного солитонов
• 3 Устойчивость солитонов
• 4 Влияние потерь мощности
  • 4.1 Генерация солитонного импульса
• 5 Темные солитоны
• 6 См. Также
• 7 Ссылки
• 8 Библиография
• 9 Внешние ссылки

Чтобы понять, как можно существовать пространственный солитон, мы должны сделать некоторые соображения о простая выпуклая линза. Как показано на рисунке справа, оптическое поле приближается к линзе, а затем фокусируется. Эффект линзы состоит в том, чтобы вызвать неравномерное изменение фазы, вызывающее фокусировку. Эта фаза изменения является функцией пространства и может быть представлена ​​с помощью $\phi \; (x)\; \{\backslash \; displaystyle\; \backslash \; varphi\; (x)\}$, форма которого представлена ​​на рисунке.

Изменение фазы можно выразить как произведение пройденной фазовой постоянной и ширины пути, поленного полем. Мы можем записать это как:

$\phi \; (x)\; =\; k\; 0\; n\; L\; (x)\; \{\backslash \; displaystyle\; \backslash \; varphi\; (x)\; =\; k\_\; \{0\}\; nL\; (x)\}$

где $L\; (x)\; \{\backslash \; displaystyle\; L\; (x)\}$- ширина линзы, изменяющаяся в каждой форме, аналогичной $\phi \; (x)\; \{\backslash \; displaystyle\; \backslash \; varphi\; (x)\}$, потому что что $k\; 0\; \{\backslash \; displaystyle\; k\_\; \{0\}\}$и являются константами. Другими словами, чтобы получить доступ к изменению фазы. Если оставить ширину L фиксированной в каждой точке, но изменить значение показателя преломления $n\; (x)\; \{\backslash \; displaystyle\; n\; (x)\}$, мыим точно такой же эффект, но с совершенно другим подходом.

Это имеет применение в световодах с градиентным коэффициентом преломления : изменение показателя преломления вводит эффект фокусировки, который может уравновесить естественную дифракцию поля. Если эти два эффекта идеально уравновешивают друг друга, то внутри волокна ограниченное поле.

Пространственные солитоны основаны на том же принципе: эффект Керра вводит фазовую самомодуляцию, которая изменяет показатель преломления в зависимости от силы:

$\phi \; (Икс)\; знак\; равно\; К\; 0\; N\; (Икс)\; L\; знак\; равно\; К\; 0\; L\; [N\; +\; N\; 2\; I\; (Икс)]\; \{\backslash \; Displaystyle\; \backslash \; varphi\; (х)\; =\; к\_\; \{0\}\; п\; (х)\; L\; =\; к\_\; \{0\}\; L\; [n\; +\; n\_\; \{2\}\; I\; (x)]\}$

если $I\; (x)\; \{\backslash \; displaystyle\; I\; (x)\}$имеет форму, аналогичную показанной на рисунке, тогда мы создали желаемое фазовое поведение, и поле покажет эффект самофокусировки. Другими словами, при распространении силовую нервную направляющую структуру. Линейные эффекты оптимизированы, не изменяются, не изменяются, не изменяются. очевидно). Чтобы получить эффект самофокусировки, мы должны иметь положительный $n\; 2\; \{\backslash \; displaystyle\; n\_\; \{2\}\}$, иначе мы получим противоположный эффект и не заметим нелинейного поведения.

Оптический волновод, создаваемый солитоном при распространении, является не только математической моделью, но и существует и другое направление движения других волн на разных частотах. Таким образом, можно использовать свету взаимодействовать со светом на разных частотах (это невозможно в линейных средах).

Доказательство

В среде распространяется электрическое поле, демонстрирующее оптический эффект Керра, поэтому показатель преломления определяет как:

$n\; (I)\; =\; n\; +\; n\; 2\; I\; \{\; \backslash \; displaystyle\; n\; (I)\; =\; n\; +\; n\_\; \{2\}\; I\}$

Напомним, что связь между энергетической освещенностью и электрическим полем (в комплексном представлении) составляет

$I\; =\; |\; E\; |\; 2\; 2\; \eta \; \{\backslash \; displaystyle\; I\; =\; \{\backslash \; frac\; \{|\; E\; |\; ^\; \{2\}\}\; \{2\; \backslash \; eta\}\}\}$

где $\eta \; =\; \eta \; 0\; /\; n\; \{\backslash \; displaystyle\; \backslash \; eta\; =\; \backslash \; eta\; \_\; \{0\}\; /\; n\}$и $\eta \; 0\; \{\backslash \; displaystyle\; \backslash \; eta\; \_\; \{0\}\}$- это импеданс свободного пространства, определяемый как

$\eta \; 0\; =\; \mu \; 0\; \epsilon \; 0\; \approx \; 377\; Ом.\; \{\backslash \; displaystyle\; \backslash \; eta\; \_\; \{0\}\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; mu\; \_\; \{0\}\}\; \{\backslash \; varepsilon\; \_\; \{0\}\}\}\}\; \backslash \; приблизительно\; 377\; \backslash \; Omega.\}$

Поле распространяется в $z\; \{\backslash \; displaystyle\; z\}$направление с фазовой $k\; 0\; n\; \{\backslash \; displaystyle\; k\_\; \{0\}\; n\}$. Сейчас мы будем игнорировать любую зависимость от оси y, предполагая, что она бесконечна в этом направлении. Тогда поле можно выразить как:

$E\; (x,\; z,\; t)\; =\; A\; ma\; (x,\; z)\; ei\; (k\; 0\; nz\; -\; \omega \; t)\; \{\backslash \; displaystyle\; E\; (x,\; z,\; t)\; =\; A\_\; \{m\}\; a\; (x,\; z)\; e\; ^\; \{i\; (k\_\; \{0\}\; nz-\; \backslash \; omega\; t)\}\}$

где $A\; m\; \{\backslash \; displaystyle\; A\_\; \{m\}\}$- это максимальная амплитуда поля и $a\; (x,\; z)\; \{\backslash \; displaystyle\; a\; (x,\; z)\}$- безразмерная нормализованная функция (так что ее максимальное значение равно 1), которая представляет собой электрическое поле между осью x. В общем, это зависит от z, потому что поля меняют свою форму при распространении. Теперь нам нужно решить уравнение Гельмгольца :

$\nabla \; 2\; E\; +\; k\; 0\; 2\; n\; 2\; (I)\; E\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; E\; +\; k\_\; \{0\}\; ^\; \{2\}\; n\; ^\; \{2\; \}\; (I)\; E\; =\; 0\}$

, где было четко указано, что показатель преломления (следовательно, фазовая постоянная) зависит от интенсивности. Если мы заменим выражение электрического поля в уравнении предполагаемой, что огибающая $a\; (x,\; z)\; \{\backslash \; displaystyle\; a\; (x,\; z)\}$медленно изменяется при распространении, т.е.

$|\; \partial \; 2\; a\; (x,\; z)\; \partial \; z\; 2\; |\; \ll \; |\; k\; 0\; \partial \; a\; (x,\; z)\; \partial \; z\; |\; \{\backslash \; displaystyle\; \backslash \; left\; |\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; a\; (x,\; z)\}\; \{\backslash \; partial\; z\; ^\; \{2\}\}\}\; \backslash \; right\; |\; \backslash \; ll\; \backslash \; left\; |\; k\_\; \{0\}\; \{\backslash \; frac\; \{\backslash \; partial\; a\; (x,\; z)\}\; \{\backslash \; partial\; z\}\}\; \backslash \; right\; |\}$

уравнение принимает следующий вид:

$\partial \; 2\; a\; \partial \; x\; 2\; +\; i\; 2\; k\; 0\; n\; \partial \; a\; \partial \; z\; +\; k\; 0\; 2\; [N\; 2\; (I)\; -\; n\; 2]\; a\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; a\}\; \{\backslash \; partial\; x\; ^\; \{2\}\}\}\; +\; i2k\_\; \{\; 0\}\; n\; \{\backslash \; frac\; \{\backslash \; partial\; a\}\; \{\backslash \; partial\; z\}\}\; +\; k\_\; \{0\}\; ^\; \{2\}\; [n\; ^\; \{2\}\; (I)\; -n\; ^\; \{2\}]\; a\; =\; 0.\}$

Давайте представим приближение, это действительно потому, что нелинейные эффекты всегда намного меньше линейных:

$[n\; 2\; (I)\; -\; n\; 2]\; =\; [n\; (I)\; -\; n]\; [n\; (I)\; +\; n]\; =\; n\; 2\; I\; (2\; n\; +\; n\; 2\; I)\; \approx \; 2\; nn\; 2\; I\; \{\backslash \; displaystyle\; [n\; ^\; \{2\}\; (I)\; -n\; ^\; \{2\}]\; =\; [n\; (I)\; -n]\; [n\; (I)\; +\; n]\; =\; n\_\; \{2\}\; I\; (2n\; +\; n\_\; \{2\}\; I)\; \backslash \; приблизительно\; 2nn\_\; \{2\}\; I\}$

теперь мы выражаем напряженность через электрическое поле:

$[n\; 2\; (I)\; -\; n\; 2]\; \approx \; 2\; nn\; 2\; |\; А\; м\; |\; 2\; |\; а\; (х,\; z)\; |\; 2\; 2\; \eta \; 0\; /\; n\; =\; n\; 2\; n\; 2\; |\; А\; м\; |\; 2\; |\; а\; (х,\; z)\; |\; 2\; \eta \; 0\; \{\backslash \; displaystyle\; [n\; ^\; \{2\}\; (I)\; -n\; ^\; \{2\}]\; \backslash \; приблизительно\; 2nn\_\; \{2\}\; \{\backslash \; frac\; \{|\; A\_\; \{m\}\; |\; ^\; \{2\}\; |\; а\; (х,\; z)\; |\; ^\; \{2\}\}\; \{2\; \backslash \; eta\; \_\; \{0\}\; /\; n\}\}\; =\; n\; ^\; \{2\}\; n\_\; \{2\}\; \{\backslash \; frac\; \{|\; A\_\; \{m\}\; |\; ^\; \{2\}\; |\; а\; (х,\; z)\; |\; ^\; \{2\}\}\; \{\backslash \; eta\; \_\; \{0\}\}\}\}$

уравнение принимает следующий вид:

$1\; 2\; k\; 0\; n\; \partial \; 2\; a\; \partial \; x\; 2\; +\; i\; \partial \; a\; \partial \; z\; +\; k\; 0\; nn\; 2\; |\; А\; м\; |\; 2\; 2\; \eta \; 0\; |\; а\; |\; 2\; a\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{2k\_\; \{0\}\; n\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; a\}\; \{\backslash \; partial\; x\; ^\; \{2\}\}\}\; +\; i\; \{\backslash \; frac\; \{\; \backslash \; partial\; a\}\; \{\backslash \; partial\; z\}\}\; +\; \{\backslash \; frac\; \{k\_\; \{0\}\; nn\_\; \{2\}\; |\; A\_\; \{m\}\; |\; ^\; \{2\}\}\; \{2\; \backslash \; eta\; \_\; \{0\}\}\}\; |\; а\; |\; ^\; \{2\}\; a\; =\; 0.\}$

Теперь предположим, что $n\; 2>0\; \{\backslash \; displaystyle\; n\_\; \{2\}>0\}$, так что нелинейный эффект вызовет самофокусировку.>n 2 = | n 2 | {\ displaystyle n_ {2} = | n_ {2} |}Давайте теперь определим некоторые параметры и заменим их в уравнении:

• $\xi \; =\; x\; X\; 0\; \{\backslash \; displaystyle\; \backslash \; xi\; =\; \{\backslash \; frac\; \{x\}\; \{X\_\; \{0\}\}\}\}$, поэтому мы можем выразить зависимость от оси x с помощью безразмерного параметра; $X\; 0\; \{\backslash \; displaystyle\; X\_\; \{0\}\; \}$- длина, физический смысл которой будет яснее позже.
• $L\; d\; =\; X\; 0\; 2\; k\; 0\; n\; \{\backslash \; displaystyle\; L\_\; \{d\}\; =\; X\_\; \{0\}\; ^\; \{2\}\; k\_\; \{0\}\; n\; \}$, после того, как нельзя электрическое поле распространилось через z для этой длины больше пренебрегать линейными эффектами дифракции.
• $\zeta \; =\; z\; L\; d\; \{\backslash \; displaystyle\; \backslash \; zeta\; =\; \{\backslash \; frac\; \{\; z\}\; \{L\_\; \{d\}\}\}\}$, для исследования z-зависимости с безразмерной батареей.
• $L\; n\; \ell \; =\; 2\; \eta \; 0\; k\; 0\; n\; |\; п\; 2\; |\; \cdot \; |\; А\; м\; |\; 2\; \{\backslash \; displaystyle\; L\_\; \{n\; \backslash \; ell\}\; =\; \{\backslash \; frac\; \{2\; \backslash \; eta\; \_\; \{0\}\}\; \{k\_\; \{0\}\; n\; |\; n\_\; \{2\}\; |\; \backslash \; cdot\; |\; A\_\; \{m\}\; |\; ^\; \{2\}\}\}\}$, после того, как электрическое поле распространилось по z на этой длине, нелинейными эффектами больше нельзя пренебрегать. Этот параметр зависит от напряженности электрического поля, что типично для нелинейных параметров.
• $N\; 2\; =\; L\; d\; L\; n\; \ell \; \{\backslash \; displaystyle\; N\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{L\_\; \{d\}\}\; \{L\_\; \{n\; \backslash \; ell\}\}\}\}$

Уравнение принимает следующий вид:

$1\; 2\; \partial \; 2\; a\; \partial \; \xi \; 2\; +\; i\; \partial \; a\; \partial \; \zeta \; +\; N\; 2\; |\; а\; |\; 2\; a\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; a\}\; \{\backslash \; partial\; \backslash \; xi\; ^\; \{2\}\}\}\; +\; i\; \{\backslash \; frac\; \{\backslash \; partial\; a\}\; \{\backslash \; partial\; \backslash \; zeta\}\}\; +\; N\; ^\; \{2\}\; |\; а\; |\; ^\; \{2\}\; a\; =\; 0\}$

это обычное уравнение, известное как нелинейное уравнение Шредингера. Из этой формы мы можем понять физический смысл параметра N:

• , если $N\; \ll \; 1\; \{\backslash \; displaystyle\; N\; \backslash \; ll\; 1\}$, то мы можем пренебречь нелинейной части уравнения. Это означает, что $L\; d\; \ll \; L\; n\; \ell \; \{\backslash \; displaystyle\; L\_\; \{d\}\; \backslash \; ll\; L\_\; \{n\; \backslash \; ell\}\}$, тогда на поле будет влиять линейный эффект (дифракция) намного раньше, чем нелинейный эффект, он будет просто дифрагировать без какого-либо нелинейного поведения.
• если $N\; \gg \; 1\; \{\backslash \; displaystyle\; N\; \backslash \; gg\; 1\}$, то нелинейный эффект будет более очевидным, чем дифракция и из-за фазовой самомодуляции, поле будет стремиться к фокусировке.
• если $N\; \approx \; 1\; \{\backslash \; displaystyle\; N\; \backslash \; приблизительно\; 1\}$, то два эффекта уравновешивают каждый другой, и мы должны решить уравнение.

Для $N\; =\; 1\; \{\backslash \; displaystyle\; N\; =\; 1\}$решение уравнения простое, и это фундаментальный солитон:

$a\; (\xi ,\; \zeta )\; знак\; равно\; sech\; \; (\xi )\; ei\; \zeta \; /\; 2\; \{\backslash \; displaystyle\; a\; (\backslash \; xi,\; \backslash \; zeta)\; =\; \backslash \; operatorname\; \{sech\}\; (\backslash \; xi)\; e\; ^\; \{i\; \backslash \; zeta\; /\; 2\}\}$

где sech - это гиперболический секанс. Это по-прежнему зависит от z, но только по фазе, поэтому форма поля не изменится во время распространения.

Для $N\; =\; 2\; \{\backslash \; displaystyle\; N\; =\; 2\}$все еще можно выразить решение в закрытой форме, но оно имеет более сложную форму:

$a\; (\xi ,\; \zeta )\; =\; 4\; [ch\; (3\; \xi )\; +\; 3\; e\; 4\; i\; \zeta \; ch\; \; (\xi )]\; ei\; \zeta \; /\; 2\; ch\; (4\; \xi )\; +\; 4\; ch\; (2\; \xi )\; +\; 3\; cos\; \; (4\; \zeta ).\; \{\backslash \; Displaystyle\; a\; (\backslash \; xi,\; \backslash \; zeta)\; =\; \{\backslash \; frac\; \{4\; [\backslash \; cosh\; (3\; \backslash \; xi)\; +\; 3e\; ^\; \{4i\; \backslash \; zeta\}\; \backslash \; cosh\; (\backslash \; xi)]\; e\; ^\; \{i\; \backslash \; zeta\; /\; 2\}\}\; \{\backslash \; ch\; (4\; \backslash \; xi)\; +4\; \backslash \; ch\; (2\; \backslash \; xi)\; +3\; \backslash \; cos\; (4\; \backslash \; zeta)\}\}.\}$

Он действительно меняет свою форму во время распространения, но это периодическая функция z с период $\zeta \; =\; \pi \; /\; 2\; \{\backslash \; displaystyle\; \backslash \; zeta\; =\; \backslash \; pi\; /\; 2\}$.

Форма солитона при распространении с N = 1, она не меняет свою форму

Форма солитона при распространении с N = 2, он меня периодическиет свою форму

Для солитонных решений N должно быть целым числом и называется порядком или солитоном. Для $N\; =\; 3\; \{\backslash \; displaystyle\; N\; =\; 3\}$также существует точное решение в закрытой форме; он имеет еще более сложный вид, но имеет ту же периодичность. Фактически, все солитоны с $N\; \ge \; 2\; \{\backslash \; displaystyle\; N\; \backslash \; geq\; 2\}$имеют период $\zeta \; =\; \pi \; /\; 2\; \{\backslash \; displaystyle\; \backslash \; zeta\; =\; \backslash \; pi\; /\; 2\}$. Их форму можно легко выразить только сразу после генерации:

$a\; (\xi ,\; \zeta \; =\; 0)\; =\; N\; sech\; \; (\xi )\; \{\backslash \; displaystyle\; a\; (\backslash \; xi,\; \backslash \; zeta\; =\; 0)\; =\; N\; \backslash \; operatorname\; \{sech\}\; (\backslash \; xi)\}$

справа - график солитона второго порядка: вначале он имеет форму сечения, максимальная амплитуда увеличивается, а затем возвращается к форме сечения. Требуется высокая интенсивность, если поле еще больше увеличит свою напряженность, среда может быть повреждена.

Условие, которое необходимо решить, если мы хотим сгенерировать фундаментальный солитон, получается выражением N через все известные параметры и последующим положением $N\; =\; 1\; \{\backslash \; displaystyle\; N\; =\; 1\}$:

$1\; =\; N\; =\; L\; d\; L\; n\; \ell \; знак\; равно\; X\; 0\; 2\; К\; 0\; 2\; N\; 2\; |\; п\; 2\; |\; |\; А\; м\; |\; 2\; 2\; \eta \; 0\; \{\backslash \; Displaystyle\; 1\; =\; N\; =\; \{\backslash \; frac\; \{L\_\; \{d\}\}\; \{L\_\; \{n\; \backslash \; ell\}\}\}\; =\; \{\backslash \; frac\; \{X\_\; \{0\}\; ^\; \{2\}\; k\_\; \{0\}\; ^\; \{2\}\; п\; ^\; \{2\}\; |\; n\_\; \{2\}\; ||\; A\_\; \{m\}\; |\; ^\; \{2\}\}\; \{2\; \backslash \; eta\; \_\; \{0\}\}\}\}$

, что в терминах максимального значения освещенности становится:

$I\; макс\; =\; |\; А\; м\; |\; 2\; 2\; \eta \; 0\; /\; n\; =\; 1\; X\; 0\; 2\; k\; 0\; 2\; n\; |\; п\; 2\; |.\; \{\backslash \; displaystyle\; I\; \_\; \{\backslash \; max\}\; =\; \{\backslash \; frac\; \{|\; A\_\; \{m\}\; |\; ^\; \{2\}\}\; \{2\; \backslash \; eta\; \_\; \{0\}\; /\; n\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{X\_\; \{0\}\; ^\; \{2\}\; k\_\; \{0\}\; ^\; \{2\}\; n\; |\; n\_\; \{2\}\; |\}\}.\}$

В большинстве случаев две переменные, которые можно изменить, - это максимальная интенсивность $I\; max\; \{\backslash \; displaystyle\; I\_\; \{\backslash \; max\}\}$и длительность импульса $X\; 0\; \{\backslash \; displaystyle\; X\_\; \{0\}\}$.

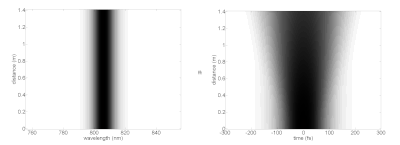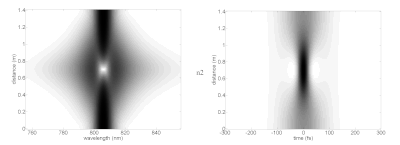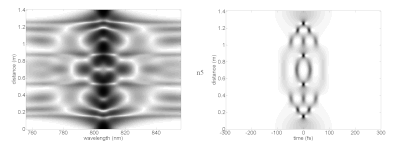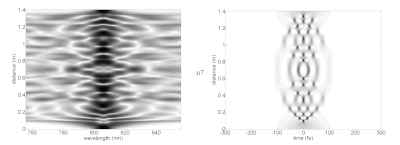
распространение различных оптических солитонов более высокого порядка (серия изображений: малой мощности (без солитона), n1-n7)

Любопытно, что солитоны более высокого порядка могут принимать сложные формы, прежде чем возвращаться точно к своей исходной форме в конце периода солитона. На изображении различных солитонов спектра (слева) и временная область (справа) показаны на различных расстояниях распространения (вертикальная ось) в идеализированной нелинейной среде. Это показывает, как лазерный импульс может вести себя при движении в среде со средствами, необходимыми для поддержки фундаментальных солитонов. Лазерные импульсы могут вводить в оптические волокна, такие как фотонно-кристаллическое волокно с сильно ограниченными распространяемыми модми. Эти имеют более широкую дисперсию и другие характеристики, которые отклоняются от аналитических параметров солитона.

Генерация пространственных солитонов

О первом эксперименте по пространственным оптическим солитонам сообщили в 1974 году Ашкин и Бьоркхольм в кювете, заполненной парами натрия. Затем эта область была пересмотрена в жидких экспериментах в Лиможском университете с тем сероуглеродом <6>и расширена в начале 90-х, когда впервые были обнаружены солитоны в фоторефрактивных кристаллах, стекле, полупроводниках и полимерах. В течение последних десятилетий сообщалось о всех открытиях в различных материалах для солитонов различной размерности, формы, спиралевидности, столкновений, слияния, расщепления, в однородных средах, периодических систем и волноводах. Пространственные солитоны также называют самозахватывающими оптическими пучками, и их формирование обычно сопровождается самозаписывающимся волноводом. В нематических жидких кристаллах пространственные солитоны также называют нематонами.

Солитоны с поперечной синхронизацией мод

Локализованные возбуждения в лазерах могут возникать из-за поперечных мод.

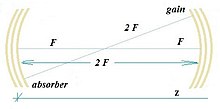
Конфокальный $2\; F\; \{\backslash \; displaystyle\; 2F\}$лазерный резонатор с нелинейным усилением и срезами поглотителя в сопряжении Фурье плоскостей

В конфокальном $2\; F\; \{\backslash \; displaystyle\; 2F\}$лазерный резонатор вырожденные поперечные моды с одной продольной модой на длине волны $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$смешанные в нелинейном диске усиления $G\; \{\backslash \; displaystyle\; G\}$(расположен в $z\; =\; 0\; \{\backslash \; displaystyle\; z\; =\; 0\}$) и диск насыщающегося поглотителя $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$(расположен в $z\; =\; 2\; F\; \{\backslash \; displaystyle\; z\; =\; 2F\}$) диаметра $D\; \{\backslash \; displaystyle\; D\}$способны образовывать пространственные солитоны гиперболического $sech\; \{\backslash \; displaystyle\; sech\}$форма: $E\; (x,\; z\; =\; 0)\; \sim \; sech\; (\pi \; x\; D\; 2\; \lambda \; F\; 1\; -\; \alpha \; GG)\; \{\backslash \; displaystyle\; E\; (x,\; z\; =\; 0)\; \backslash \; sim\; \{\backslash \; rm\; \{sech\}\; \}\; \backslash \; left\; (\backslash !\; \{\backslash \; frac\; \{\backslash \; pi\; xD\}\; \{2\; \backslash \; lambda\; F\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{1-\; \backslash \; alpha\; G\}\; \{G\}\}\}\; \backslash ,\; \backslash \; right)\}$

$E\; (\; x,\; z\; =\; 2\; F)\; \sim \; sech\; (2\; \pi \; x\; DG\; 1\; -\; \alpha \; G)\; \{\backslash \; Displaystyle\; E\; (x,\; z\; =\; 2F)\; \backslash \; sim\; \{\backslash \; rm\; \{sech\}\}\; \backslash \; left\; (\backslash !\; \{\backslash \; fr\; ac\; \{2\; \backslash \; pi\; x\}\; \{D\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{G\}\; \{1-\; \backslash \; alpha\; G\}\}\}\; \backslash ,\; \backslash \; right)\}$

в сопряженных Фурье плоскостности $z\; =\; 0\; \{\backslash \; displaystyle\; z\; =\; 0\}$и $z\; =\; 2\; F\; \{\backslash \; displaystyle\; z\; =\; 2F\}$.

Основная проблема, ограничивающая передачу битрейт в оптических волокнах - это дисперсия групповой скорости. Это тем, что генерируются импульсами имеют ненулевую полосу пропускания, среда, в которой они распространяются, имеет показатель преломления, который зависит от частоты (или длины волны ). Этот эффект представлен параметром дисперсии групповой задержки D; с его помощью можно точно рассчитать, насколько расширится импульс:

$\Delta \; \tau \; \approx \; DL\; \Delta \; \lambda \; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \; tau\; \backslash \; приблизительно\; DL\; \backslash ,\; \backslash \; Delta\; \backslash \; lambda\}$

где L - длина волокна, а $\Delta \; \lambda \; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \; lambda\}$- ширина полосы частот в единицах длины волны. Подход в современных системах связи заключается в том, чтобы сбалансировать такую ​​дисперсию с другими волокнами, имеющими D с разными знаками в разных волокнах: таким образом, импульсы продолжают расширяться и сжиматься при распространении. С помощью временных солитонов можно полностью снять эту проблему.

линейные и нелинейные эффекты на гауссовых импульсах

Рассмотрим рисунок справа. Слева показан стандартный импульс Гаусса, который представляет собой огибающую поля, колеблющегося с определенным качеством. Мы предполагаем, что частота постоянно постоянно во время импульсса.

Теперь мы позволяем этому импульсу распространяться по волокну с $D>0\; \{\backslash \; displaystyle\; D>0\}$будет зависеть от дисперсии групповых скоростей. Для этого знака D дисперсия аномальная частота Общий сигнал, который мы получаем, представляет собой более широкий чирпированный импульс, показанный в верхнем углу изображения.

влияние фазовой самомодуляции на частоту

Теперь предположим, что у нас есть среда, которая демонстрирует только нелинейный эффект Керра, но ее показатель преломления не зависит от частоты: такая среда не существует, но стоит рассмотреть его, чтобы понять различные эффекты.

Фаза поля определяется как:

$\phi \; (t)\; =\; \omega \; 0\; T\; -\; kz\; знак\; равно\; \omega \; 0\; T\; -\; К\; 0\; Z\; [N\; +\; N\; 2\; I\; (T)]\; \{\backslash \; displaystyle\; \backslash \; varphi\; (t)\; =\; \backslash \; omega\; \_\; \{0\}\; t-kz\; =\; \backslash \; omega\; \_\; \{0\}\; t-\; k\_\; \{0\}\; z\; [n\; +\; n\_\; \{2\}\; I\; (t)]\}$

частота (согласно его определению) задается следующим образом:

$\omega \; (t)\; =\; \partial \; \phi \; (t)\; \partial \; t\; =\; \omega \; 0\; -\; К\; 0\; ZN\; 2\; \partial \; I\; (T)\; \partial \; T\; \{\backslash \; Displaystyle\; \backslash \; omega\; (t)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; varphi\; (t)\}\; \{\backslash \; partial\; t\}\}\; =\; \backslash \; omega\; \_\; \{0\}\; -k\_\; \{0\}\; zn\_\; \{2\}\; \{\backslash \; frac\; \{\backslash \; partial\; I\; (t)\}\; \{\backslash \; partial\; t\}\}\}$

представлена ​​на рисунке слева. В начале частоты ниже, в конце выше. После прохождения через нашу идеальную среду мы получим чирпированный импульс без уширения, потому что мы пренебрегли дисперсией.

Возвращаясь к первому изображению, мы видим, что два эффекта вызывают изменение частоты в двух разных противоположных направлениях. Можно создать импульс, чтобы два эффекта уравновешивали друг друга. Учитывая более высокие частоты, линейная дисперсия будет способствовать их более быстрому распространению, в то время как нелинейный эффект Керра замедлит их. Общий эффект будет заключаться в том, что импульс не изменяется при распространении: такие импульсы называются временными солитонами.

История временных солитонов

В 1973 году Акира Хасегава и Фред Тапперт из ATT Bell Labs были первыми, кто предположил, что солитоны могут существовать в оптических волокнах из-за баланса между фазовой самомодуляцией и аномальной дисперсией. Также в 1973 г. Робин Буллоу сделал первое математическое сообщение о существовании оптических солитонов. Он также использует идею системы передачи на солитонов для повышения производительности оптических телекоммуникаций.

Солитоны в волоконно-оптической системе описываются уравнениями Манакова.

. В 1987 г. P. Emplit, JP Hamaide, F. Reynaud, C. Froehly и A. Barthelemy из университетов Брюсселя и Лиможа провели первое экспериментальное наблюдение распространения темного солитона в оптическом волокне.

В 1988 году Линн Молленауэр и его команда передали солитонные импульсы на расстоянии более 4000 километров, используя явление, называемое эффектом Рамана, названное в честь индийского ученого сэра К.В. Рамана, который первым описал это в 1920-х годах, чтобы обеспечить волокно.

В 1991 году исследовательская группа Bell Labs безошибочно передавала солитоны на скорости 2,5 гигабита на расстояние более 14000 километров, используя эрбиевые оптоволоконные усилители (сращенные сегменты оптического волокна, редкие земные элементы эрбий). Лазеры накачки, подключенные к оптическим усилителям, активируют эрбий, который возбуждает световые импульсы.

В 1998 году Тьерри Жорж и его команда из France Télécom RD Center, комбинируя оптические солитоны с разными длинами волн (мультиплексирование с разделением по длине волны ), данные передачи данных 1 терабит в секунду (1 000 000 000 000 единиц информации в секунду).

В 2020 году компания Optics Communications сообщила о японской команде из MEXT, коммутации оптических каналов с пропускной способностью до 90 Тбит / с (терабит в секунду), Optics Communications, том 466, 1 июля 2020 года, 125677.

Доказательство для временных солитонов

Электрическое поле распространяется в среде, демонстрируя оптический эффект Керра, через направляющую структуру (такую ​​как оптическое волокно ), которая ограничивает мощность в плоскости xy. Если поле распространяется в сторону z с фазовой постоянной $\beta \; 0\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{0\}\}$, то это можно выразить в следующей форме:

$E\; (r,\; T)\; знак\; равно\; A\; ma\; (T,\; Z)\; е\; (Икс,\; Y)\; EI\; (\beta \; 0\; Z\; -\; \omega \; 0\; T)\; \{\backslash \; Displaystyle\; E\; (\backslash \; mathbf\; \{r\},\; t)\; =\; A\_\; \{m\}\; a\; (t,\; z)\; е\; (х,\; у)\; е\; ^\; \{я\; (\backslash \; бета\; \_\; \{0\}\; z-\; \backslash \; omega\; \_\; \{0\}\; t)\}\}$

где $A\; m\; \{\backslash \; displaystyle\; A\_\; \{m\}\}$- максимальная амплитуда поля, $a\; (t,\; z)\; \{\backslash \; displaystyle\; a\; (t,\; z)\}$- огибающая, которая формирует импульс во временной области; в общем, это зависит от z, потому что импульс может изменить свою форму при распространении; $f\; (x,\; y)\; \{\backslash \; displaystyle\; f\; (x,\; y)\}$представляет формулу поля в плоскости xy, и она не меняется во время распространения, как мы предположили, что поле управляемый. И используются нормализованные безразмерные функции, максимальное значение которых равно 1, так что $A\; m\; \{\backslash \; displaystyle\; A\_\; \{m\}\}$действительно представляет амплитуду поля.

в среде присутствует дисперсия, которая не позволяет пренебречь, связь между электрическим полем и его поляризацией задается интегралом свертки. В любом случае использования в Фурье, мы можем заменить свертку простым, используя таким образом, стандартные отношения, действительные в более простые средах. Мы преобразуем электрическое поле по Фурье, используя следующее определение:

$E\; ~\; (r,\; \omega \; -\; \omega \; 0)\; =\; \int \; -\; \infty \; \infty \; E\; (r,\; t)\; e\; -\; i\; (\omega \; -\; \omega \; 0)\; tdt\; \{\backslash \; displaystyle\; \{\backslash \; тильда\; \{E\}\}\; (\backslash \; mathbf\; \{r\},\; \backslash \; omega\; -\; \backslash \; omega\; \_\; \{0\})\; =\; \backslash \; int\; \backslash \; limits\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; E\; (\backslash \; mathbf\; \{r\},\; t)\; e\; ^\; \{-\; i\; (\backslash \; omega\; -\; \backslash \; omega\; \_\; \{0\})\; t\}\; \backslash ,\; dt\}$

Используя это определение, производная во временной области соответствует произведению в области Фурье:

$\partial \; \partial \; t\; E\; ⟺\; я\; (\omega \; -\; \omega \; 0)\; E\; ~\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; t\}\}\; E\; \backslash \; Longleftrightarrow\; i\; (\backslash \; omega\; -\; \backslash \; omega\; \_\; \{0\})\; \{\backslash \; tilde\; \{E\}\}\}$

полное выражение поля в частотной области:

$E\; ~\; (r,\; \omega \; -\; \omega \; 0)\; =\; A\; ma\; ~\; (\omega ,\; z)\; f\; (x,\; y)\; ei\; \beta \; 0\; z\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{E\}\}\; (\backslash \; mathbf\; \{r\; \},\; \backslash \; omega\; -\; \backslash \; omega\; \_\; \{0\})\; =\; A\_\; \{m\}\; \{\backslash \; tilde\; \{a\}\}\; (\backslash \; omega,\; z)\; f\; (x,\; y)\; e\; ^\; \{i\; \backslash \; beta\; \_\; \{0\}\; z\}\}$

Теперь мы можем решить уравнение Гельмгольца в частотной области:

$\nabla \; 2\; E\; ~\; +\; n\; 2\; (\omega )\; k\; 0\; 2\; E\; ~\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; \{\backslash \; tilde\; \{E\}\}\; +\; n\; ^\; \{2\}\; (\backslash \; omega)\; k\_\; \{0\}\; ^\; \{2\}\; \{\backslash \; tilde\; \{E\}\}\; =\; 0\}$

мы решаем expre ss фазовая постоянная со следующими обозначениями:

$n\; (\omega )\; k\; 0\; =\; \beta \; (\; \omega )\; =\; \beta \; 0\; ⏞\; линейный\; недисперсионный\; +\; \beta \; \ell \; (\omega )\; ⏞\; линейный\; дисперсионный\; +\; \beta \; n\; \ell \; ⏞\; нелинейное\; =\; \beta \; 0\; +\; \Delta \; \beta \; (\omega )\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; n\; (\backslash \; omega)\; k\_\; \{0\}\; =\; \backslash \; beta\; (\backslash \; omega)\; =\; \backslash \; overbrace\; \{\backslash \; beta\; \_\; \{0\}\}\; ^\; \{\backslash \; text\; \{линейная\; недисперсия\}\}\; +\; \backslash \; overbrace\; \{\backslash \; beta\; \_\; \{\backslash \; ell\}\; (\backslash \; omega)\}\; ^\; \{\backslash \; text\; \{линейная\; дисперсия\}\}\; +\; \backslash \; overbrace\; \{\backslash \; beta\; \_\; \{n\; \backslash \; ell\}\}\; ^\; \{\backslash \; text\; \{non-linear\}\}\; \backslash \backslash \; [8pt]\; =\; \backslash \; beta\; \_\; \{0\}\; +\; \backslash \; Delta\; \backslash \; beta\; (\backslash \; omega)\; \backslash \; end\; \{align\}\}\}$

где мы предполагаем, что $\Delta \; \beta \; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \; beta\}$(сумма линейной дисперсии составляющей и нелинейной части) представляет собой небольшое возмущение, т.е. $|\; \beta \; 0\; |\; \gg \; |\; \Delta \; \beta \; (\omega )\; |\; \{\backslash \; displaystyle\; |\; \backslash \; beta\; \_\; \{0\}\; |\; \backslash \; gg\; |\; \backslash \; Delta\; \backslash \; beta\; (\backslash \; omega)\; |\}$. Фазовая постоянная может иметь любое сложное поведение, но мы можем использовать ее с помощью ряда Тейлора с центром на $\omega \; 0\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{0\}\}$:

$\beta \; (\omega )\; \approx \; \beta \; 0\; +\; (\omega \; -\; \omega \; 0)\; \beta \; 1\; +\; (\omega \; -\; \omega \; 0)\; 2\; 2\; \beta \; 2\; +\; \beta \; N\; \ell \; \{\backslash \; displaystyle\; \backslash \; beta\; (\backslash \; omega)\; \backslash \; приблизительно\; \backslash \; beta\; \_\; \{0\}\; +\; (\backslash \; omega\; -\; \backslash \; omega\; \_\; \{0\})\; \backslash \; beta\; \_\; \{1\}\; +\; \{\backslash \; frac\; \{(\backslash \; omega\; -\; \backslash \; omega\; \_\; \{0\})\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; beta\; \_\; \{2\}\; +\; \backslash \; beta\; \_\; \{n\; \backslash \; ell\}\; \}$

где, как известно:

$\beta \; u\; =\; du\; \beta \; (\omega )\; d\; \omega \; u\; |\; \omega \; знак\; равно\; \omega \; 0\; \{\backslash \; Displaystyle\; \backslash \; beta\; \_\; \{u\}\; =\; \backslash \; влево.\; \{\backslash \; frac\; \{d\; ^\; \{u\}\; \backslash \; beta\; (\backslash \; omega)\}\; \{d\; \backslash \; omega\; ^\; \{u\}\}\}\; \backslash \; right\; |\; \_\; \{\backslash \; omega\; =\; \backslash \; omega\; \_\; \{0\}\}\}$

мы подставляем выражение электрического поля в уравнении и делаем некоторые вычисления. Если принять приближение медленно меняющейся огибающей :

$|\; \partial \; 2\; a\; ~\; \partial \; z\; 2\; |\; \ll \; |\; \beta \; 0\; \partial \; a\; ~\; \partial \; z\; |\; \{\backslash \; displaystyle\; \backslash \; left\; |\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \{\backslash \; tilde\; \{a\}\}\}\; \{\backslash \; partial\; z\; ^\; \{2\}\}\}\; \backslash \; right\; |\; \backslash \; ll\; \backslash \; left\; |\; \backslash \; beta\; \_\; \{0\}\; \{\backslash \; frac\; \{\backslash \; partial\; \{\backslash \; tilde\; \{a\}\}\}\; \{\backslash \; partial\; z\}\}\; \backslash \; right\; |\}$

получаем:

$2\; i\; \beta \; 0\; \partial \; a\; ~\; \partial \; z\; +\; [\beta \; 2\; (\omega )\; -\; \beta \; 0\; 2]\; a\; ~\; =\; 0\; \{\backslash \; displaystyle\; 2i\; \backslash \; beta\; \_\; \{0\}\; \{\backslash \; frac\; \{\backslash \; partial\; \{\backslash \; tilde\; \{a\}\}\}\; \{\backslash \; partial\; z\}\}\; +\; [\backslash \; beta\; ^\; \{2\; \}\; (\backslash \; omega)\; -\; \backslash \; beta\; \_\; \{0\}\; ^\; \{2\}]\; \{\backslash \; tilde\; \{a\}\}\; =\; 0\}$

мы игнорируем поведение в плоскости xy, потому что оно уже известно и задается как $f\; (\; х,\; у)\; \{\backslash \; Displaystyle\; F\; (х,\; у)\}$. Сделаем небольшое приближение, как и для пространственного солитона:

$\beta \; 2\; (\omega )\; -\; \beta \; 0\; 2\; =\; [\beta \; (\omega )\; -\; \beta \; 0]\; [\beta \; (\omega )\; +\; \beta \; 0]\; =\; [\beta \; 0\; +\; \Delta \; \beta \; (\omega )\; -\; \beta \; 0]\; [2\; \beta \; 0\; +\; \Delta \; \beta \; (\omega )]\; \approx \; 2\; \beta \; 0\; \Delta \; \beta \; (\omega )\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; beta\; ^\; \{2\}\; (\backslash \; omega)\; -\; \backslash \; бета\; \_\; \{0\; \}\; ^\; \{2\}\; =\; [\backslash \; beta\; (\backslash \; omega)\; -\; \backslash \; beta\; \_\; \{0\}]\; [\backslash \; beta\; (\backslash \; omega)\; +\; \backslash \; beta\; \_\; \{0\}]\; \backslash \backslash \; [6pt]\; =\; [\backslash \; beta\; \_\; \{0\; \}\; +\; \backslash \; Delta\; \backslash \; beta\; (\backslash \; omega)\; -\; \backslash \; beta\; \_\; \{0\}]\; [2\; \backslash \; beta\; \_\; \{0\}\; +\; \backslash \; Delta\; \backslash \; beta\; (\backslash \; omega)]\; \backslash \; приблизительно\; 2\; \backslash \; beta\; \_\; \{0\}\; \backslash \; \backslash \; Delta\; \backslash \; beta\; (\backslash \; omega)\; \backslash \; end\; \{align\}\}\}$

заменяя это в уравнении, мы просто получаем:

$i\; \partial \; a\; ~\; \partial \; z\; +\; \Delta \; \beta \; (\omega )\; a\; ~\; =\; 0\; \{\backslash \; displaystyle\; i\; \{\backslash \; frac\; \{\; \backslash \; partial\; \{\backslash \; tilde\; \{a\}\}\}\; \{\backslash \; partial\; z\}\}\; +\; \backslash \; Delta\; \backslash \; beta\; (\backslash \; omega)\; \{\backslash \; tilde\; \{a\}\}\; =\; 0\}$.

Теперь мы хотим вернуться в временную область. Выражая произведения производными, мы получаем двойственность:

$\Delta \; \beta \; (\omega )\; ⟺\; я\; \beta \; 1\; \partial \; \partial \; t\; -\; \beta \; 2\; 2\; \partial \; 2\; \partial \; t\; 2\; +\; \beta \; N\; \ell \; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \; beta\; (\backslash \; omega)\; \backslash \; Longleftrightarrow\; i\; \backslash \; beta\; \_\; \{1\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; t\}\}\; -\; \{\backslash \; frac\; \{\backslash \; beta\; \_\; \{2\}\}\; \{2\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\}\; \{\backslash \; partial\; t\; ^\; \{2\}\}\}\; +\; \backslash \; beta\; \_\; \{n\; \backslash \; ell\}\}$

мы можем записывать нелинейную составляющую в терминах освещенности или амплитуды поля:

$\beta \; n\; \ell \; =\; k\; 0\; n\; 2\; I\; =\; k\; 0\; n\; 2\; |\; E\; |\; 2\; 2\; \eta \; 0\; /\; n\; =\; k\; 0\; n\; 2\; n\; |\; А\; м\; |\; 2\; 2\; \eta \; 0\; |\; а\; |\; 2\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{n\; \backslash \; ell\}\; =\; k\_\; \{0\}\; n\_\; \{2\}\; I\; =\; k\_\; \{0\}\; n\_\; \{2\}\; \{\backslash \; frac\; \{|\; E\; |\; ^\; \{2\}\}\; \{2\; \backslash \; eta\; \_\; \{0\}\; /\; n\}\}\; =\; k\_\; \{0\}\; n\_\; \{2\}\; n\; \{\backslash \; frac\; \{|\; A\_\; \{m\}\; |\; ^\; \{2\}\}\; \{2\; \backslash \; eta\; \_\; \{0\}\}\}\; |\; а\; |\; ^\; \{2\}\}$

для двойственности с пространственным солитоном определим:

$L\; n\; \ell \; =\; 2\; \eta \; 0\; k\; 0\; nn\; 2\; |\; А\; м\; |\; 2\; \{\backslash \; displaystyle\; L\_\; \{n\; \backslash \; ell\}\; =\; \{\backslash \; frac\; \{2\; \backslash \; eta\; \_\; \{0\}\}\; \{k\_\; \{0\}\; nn\_\; \{2\}\; |\; A\_\; \{m\}\; |\; ^\; \{2\}\}\}\}$

и это символ имеет то же значение, что и в предыдущем случае, даже если контекст отличается. Уравнение принимает следующий вид:

$i\; \partial \; a\; \partial \; z\; +\; i\; \beta \; 1\; \partial \; a\; \partial \; t\; -\; \beta \; 2\; 2\; \partial \; 2\; a\; \partial \; t\; 2\; +\; 1\; L\; n\; \ell \; |\; а\; |\; 2\; a\; =\; 0\; \{\backslash \; displaystyle\; i\; \{\backslash \; frac\; \{\backslash \; partial\; a\}\; \{\backslash \; partial\; z\}\}\; +\; i\; \backslash \; beta\; \_\; \{1\}\; \{\backslash \; frac\; \{\backslash \; partial\; a\}\; \{\backslash \; partial\; t\}\}\; -\; \{\backslash \; frac\; \{\backslash \; бета\; \_\; \{2\}\}\; \{2\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; a\}\; \{\backslash \; partial\; t\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{L\_\; \{n\; \backslash \; ell\}\}\}\; |\; а\; |\; ^\; \{2\}\; a\; =\; 0\}$

Мы знаем, что импульс распространения вдоль оси z совой скоростью , заданной как $vg\; =\; 1\; /\; \beta \; 1\; \{\backslash \; displaystyle\; v\_\; \{g\}\; =\; 1\; /\; \backslash \; beta\; \_\; \{1\}\}$, поэтому нас это не интересует, потому что мы просто хотим знать, как импульс меняет свою форму при распространении. Мы решаем форму импульса, то есть огибающую функцию функции (·), используя эталон, который движется с полем с той же скоростью. Таким образом, мы делаем замену

$T\; =\; t\; -\; \beta \; 1\; z\; \{\backslash \; displaystyle\; T\; =\; t-\; \backslash \; beta\; \_\; \{1\}\; z\}$

, и уравнение принимает следующий вид:

$i\; \partial \; a\; \partial \; z\; -\; \beta \; 2\; 2\; \partial \; 2\; a\; \partial \; T\; 2\; +\; 1\; L\; n\; \ell \; |\; а\; |\; 2\; a\; =\; 0\; \{\backslash \; displaystyle\; i\; \{\backslash \; frac\; \{\backslash \; partial\; a\}\; \{\backslash \; partial\; z\}\}\; -\; \{\backslash \; frac\; \{\backslash \; beta\; \_\; \{2\}\}\; \{2\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; a\}\; \{\backslash \; partial\; T\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{L\_\; \{n\; \backslash \; ell\}\}\}\; |\; а\; |\; ^\; \{2\}\; a\; =\; 0\}$

Далее предположим, что среда, в которой представлен, показывает аномальную дисперсию, то есть или с точки зрения дисперсии групповой задержки $D\; =\; -\; 2\; \pi \; c\; \lambda \; 2\; \beta \; 2>0\; \{\backslash \; displaystyle\; D\; =\; \{\backslash \; frac\; \{-2\; \backslash \; pi\; c\}\; \{\backslash \; lambda\; ^\; \{2\}\}\}\; \backslash \; beta\; \_\; \{2\}>0\}$. Мы делаем более очевидную замену. в уравнении $\beta \; 2\; =\; -\; |\; \beta \; 2\; |\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{2\}\; =\; -\; |\; \backslash \; beta\; \_\; \{2\}\; |\}$. Определим теперь следующие параметры (двойственность с предыдущим случаем очевидна):

$L\; d\; =\; T\; 0\; 2\; |\; \beta \; 2\; |;\; \tau \; =\; TT\; 0;\; \zeta \; =\; z\; L\; d;\; N\; 2\; =\; L\; d\; LN\; \ell \; \{\backslash \; displaystyle\; L\_\; \{d\}\; =\; \{\backslash \; frac\; \{T\_\; \{0\}\; ^\; \{2\}\}\; \{|\; \backslash \; beta\; \_\; \{2\}\; |\}\};\; \backslash \; qquad\; \backslash \; tau\; =\; \{\backslash \; frac\; \{T\}\; \{T\_\; \{0\}\}\};\; \backslash \; qquad\; \backslash \; zeta\; =\; \{\backslash \; frac\; \{z\}\; \{L\_\; \{\; d\}\}\};\; \backslash \; qquad\; N\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{L\_\; \{d\}\}\; \{L\_\; \{n\; \backslash \; ell\}\}\}\}$

заменяя их в уравнении, получаем:

$1\; 2\; \partial \; 2\; a\partial \; \tau \; 2\; +\; i\; \partial \; a\; \partial \; \zeta \; +\; N\; 2\; |\; а\; |\; 2\; a\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; a\}\; \{\backslash \; partial\; \backslash \; tau\; ^\; \{2\}\}\}\; +\; i\; \{\backslash \; frac\; \{\backslash \; partial\; a\}\; \{\backslash \; partial\; \backslash \; zeta\}\}\; +\; N\; ^\; \{2\}\; |\; а\; |\; ^\; \{2\}\; a\; =\; 0\}$

, которое является точно таким же уравнением, которое мы получили в предыдущем случае. Солитон первого порядка определяется выражением:

$a\; (\tau ,\; \zeta )\; =\; sech\; \; (\tau )\; ei\; \zeta \; /\; 2\; \{\backslash \; displaystyle\; a\; (\backslash \; tau,\; \backslash \; zeta)\; =\; \backslash \; operatorname\; \{sech\}\; (\backslash \; tau)\; e\; ^\; \{i\; \backslash \; zeta\; /\; 2\}\}$

те же соображения, которые мы сделали, справедливы и в этом случае. Условие N = 1 становится условием амплитуды электрического поля:

$|\; А\; м\; |\; 2\; =\; 2\; \eta \; 0\; |\; \beta \; 2\; |\; Т\; 0\; 2\; N\; 2\; К\; 0\; N\; \{\backslash \; Displaystyle\; |\; A\_\; \{m\}\; |\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{2\; \backslash \; eta\; \_\; \{0\}\; |\; \backslash \; beta\; \_\; \{2\}\; |\}\; \{T\_\; \{0\}\; ^\; \{2\}\; n\_\; \{2\}\; k\_\; \{0\}\; n\}\}\}$

или, с точки зрения освещенности:

$I\; max\; =\; |\; А\; м\; |\; 2\; 2\; \eta \; 0\; /\; n\; =\; |\; \beta \; 2\; |\; T\; 0\; 2\; N\; 2\; К\; 0\; \{\backslash \; Displaystyle\; I\; \_\; \{\backslash \; max\}\; =\; \{\backslash \; frac\; \{|\; A\_\; \{m\}\; |\; ^\; \{2\}\}\; \{2\; \backslash \; eta\; \_\; \{0\}\; /\; n\}\}\; =\; \{\backslash \; frac\; \{|\; \backslash \; beta\; \_\; \{2\}\; |\}\; \{T\_\; \{0\}\; ^\; \{2\}\; n\_\; \{2\}\; k\_\; \{0\}\}\}\}$

или мы можем выразить это в терминах мощности, если введем эффективную площадь $A\; eff\; \{\backslash \; displaystyle\; A\; \_\; \{\backslash \; text\; \{eff\}\}\}$определено так, что $P\; =\; IA\; eff\; \{\backslash \; displaystyle\; P\; =\; IA\; \_\; \{\backslash \; text\; \{eff\}\}\}$:

$P\; =\; |\; \beta \; 2\; |\; A\; эфф\; T\; 0\; 2\; N\; 2\; К\; 0\; \{\backslash \; Displaystyle\; P\; =\; \{\backslash \; frac\; \{|\; \backslash \; beta\; \_\; \{2\}\; |\; A\; \_\; \{\backslash \; text\; \{eff\}\}\}\; \{T\_\; \{0\}\; ^\; \{2\}\; n\_\; \{2\}\; k\_\; \{\; 0\}\}\}\}$

Мы описали, что такое оптические солитоны, и, используя математику, мы увидели, что если мы хотим их создать, мы должны создать поле с определенным форма (просто sech для первого порядка) с определенной мощностью, связанной с длительностью импульса. Но что, если мы немного ошиблись в создании таких импульсов? Добавляя небольшие возмущения в уравнения и решая их численно, можно показать, что одномерные солитоны устойчивы. Их часто называют (1 + 1) D-солитонами, что означает, что они ограничены в одном измерении (x или t, как мы видели) и распространяются в другом (z).

Если мы создадим такой солитон, используя немного неправильную мощность или форму, то он будет сам настраиваться, пока не достигнет стандартной формы сечения с правильной степенью. К сожалению, это достигается за счет некоторой потери мощности, которая может вызвать проблемы, поскольку может генерировать другое несолитонное поле, распространяющееся вместе с желаемым полем. Одномерные солитоны очень стабильны: например, если , мы все равно сгенерируем солитон первого порядка; если N больше, мы сгенерируем солитон более высокого порядка, но его фокусировка при распространении может вызвать пики большой мощности, повреждающие среду.

Единственный способ создать пространственный солитон (1 + 1) D - это ограничить поле по оси y с помощью диэлектрической пластины, а затем ограничить поле по x с помощью солитона.

С другой стороны, пространственные солитоны (2 + 1) D нестабильны, поэтому любое небольшое возмущение (например, из-за шума) может вызвать дифракцию солитона в виде поля в линейной среде или коллапс., повреждая материал. Можно создать стабильные (2 + 1) пространственные солитоны D, используя насыщающую нелинейную среду, где соотношение Керра $n\; (I)\; =\; n\; +\; n\; 2\; I\; \{\backslash \; displaystyle\; n\; (I)\; =\; n\; +\; n\_\; \{2\}\; I\}$действителен до тех пор, пока не достигнет максимального значения. Работа вблизи этого уровня насыщения позволяет создать устойчивый солитон в трехмерном пространстве.

Если мы рассмотрим распространение коротких (временных) световых импульсов или больших расстояний, необходимо учитывать поправки более высокого порядка, и поэтому огибающая несущей импульса регулируется нелинейным уравнением Шредингера высокого порядка (HONSE), для которого есть некоторые специализированные (аналитические) солитоны решения.

Как мы видели, для создания солитона необходимо иметь правильную мощность при его генерации. Если в среде нет потерь, то мы знаем, что солитон будет продолжать распространяться вечно, не меня меня формы (1-й порядок) или периодически изменяя свою форму (более высокие порядки). К сожалению, любая среда приводит к кям, поэтому фактическое поведение мощности будет иметь вид:

$P\; (z)\; =\; P\; 0\; e\; -\; \alpha \; z\; \{\backslash \; displaystyle\; P\; (z)\; =\; P\_\; \{0\}\; e\; ^\; \{-\; \backslash \; alpha\; z\; \}\}$

это серьезная проблема для временных солитонов, распространяющихся в волокнах на несколько километров. Рассмотрим, что происходит с временным солитоном, сразу же обобщение на пространственные пространственные объекты. Мы доказали, что связь между мощностью $P\; 0\; \{\backslash \; displaystyle\; P\_\; \{0\}\}$и длиной импульса $T\; 0\; \{\backslash \; displaystyle\; T\_\; \{0\}\}$является:

$P\; =\; |\; \beta \; 2\; |\; A\; эфф\; T\; 0\; 2\; N\; 2\; К\; 0\; \{\backslash \; Displaystyle\; P\; =\; \{\backslash \; frac\; \{|\; \backslash \; beta\; \_\; \{2\}\; |\; A\; \_\; \{\backslash \; text\; \{eff\}\}\}\; \{T\_\; \{0\}\; ^\; \{2\}\; n\_\; \{2\}\; k\_\; \{0\}\}\}\}$

при изменении мощности единственное, что может измениться во второй части отношения, - это $Т\; 0\; \{\backslash \; displaystyle\; T\_\; \{0\}\}$. если мы добавим потери к мощности и решим соотношение в терминах $T\; 0\; \{\backslash \; displaystyle\; T\_\; \{0\}\}$, мы получим:

$T\; (z)\; =\; T\; 0\; e\; (\alpha \; /\; 2)\; z\; \{\backslash \; displaystyle\; T\; (z)\; =\; T\_\; \{0\}\; e\; ^\; \{(\backslash \; alpha\; /\; 2)\; z\}\}$

ширина импульса растет экспоненциально, чтобы уравновесить потери! это соотношение верно до тех пор, пока существует солитон, т.е. пока это возмущение должно быть не будет небольшим, поэтому оно должно быть $\alpha \; z\; \ll \; 1\; \{\backslash \; displaystyle\; \backslash \; alpha\; z\; \backslash \; ll\; 1\}$иначе мы можем использовать уравнения для солитонов, и мы должны изучить стандартную линейную дисперсию. Если мы хотим создать систему передачи с использованием оптических волокон и солитонов, мы должны добавить оптические усилители, чтобы ограничить потери мощности.

Создание ионного солитонного импульса

Были проведены эксперименты по анализу воздействия высокочастотного (20 МГц - 1 ГГц) внешнего магнитного поля, индуцированного нелинейным эффектом Керра на одномодовое оптическое волокно длины. (50–100 м) для компенсации дисперсии групповой скорости (ДГС) и эволюции солитонного импульса (пиковая энергия, узкая,). Генерация солитонного импульса в волокне - очевидный вывод, так как фазовая самомодуляция из-за высокой энергии с импульса GVD, тогда как длина эволюции составляет 2000 км. (длина волны лазера выбрана больше 1,3 микрометра). Кроме того, пиковый солитонный импульс имеет период 1–3 пс, так что он надежно размещается в оптической полосе пропускания. После генерации солитонного сигнала он меньше всего рассеивается по оптоволокну длиной в тысячи километров, что ограничивает количество ретрансляционных станций.

При рассмотрении обоих типов солитонов выдвигаются условия, касающиеся среды:

• в пространственных солитонах, $n\; 2>0\; \{\backslash \; displaystyle\; n\_\; \{2\}>0\}$, это означает, что фазовая самомодуляция вызывает самофокусировку
• во временных солитонах, или $D>0\; \{\backslash \; displaystyle\; D>0\}$, аномальная дисперсия

если можно получить солитоны, эти условия не проверены? если мы предположим или $\beta \; 2>0\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{2\}>0\}$, мы получим следующее уравнение (оно имеет одинаковую формулу в обоих случаях, мы получим следующее уравнение только обозначение временного солитона):

$-\; 1\; 2\; \partial \; 2\; a\; \partial \; \tau \; 2\; +\; i\; \partial \; a\; \partial \; \zeta \; +\; N\; 2\; |\; a\; |\; 2\; a\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{-1\}\; \{2\}\}\; \{\; \backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; a\}\; \{\backslash \; partial\; \backslash \; tau\; ^\; \{2\}\}\}\; +\; i\; \{\backslash \; frac\; \{\backslash \; partial\; a\}\; \{\backslash \; partial\; \backslash \; zeta\}\}\; +\; N\; ^\; \{2\}\; |\; a\; |\; ^\; \{\; 2\}\; a\; =\; 0.\}$

Это уравнение имеет солитоноподобные решения. Для первого порядка (N = 1):

$a\; (\tau ,\; \zeta )\; =\; tanh\; \; (\tau )\; ei\; \zeta .\; \{\backslash \; Displaystyle\; a\; (\backslash \; tau,\; \backslash \; zeta)\; =\; \backslash \; tanh\; (\backslash \; tau)\; e\; ^\; \{i\; \backslash \; zeta\}.\; \backslash \}$

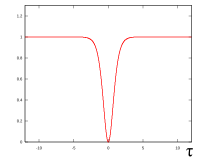
мощность темного солитона

График $|\; a\; (\tau ,\; \zeta )\; |\; 2\; \{\backslash \; displaystyle\; |\; a\; (\backslash \; tau,\; \backslash \; zeta)\; |\; ^\; \{2\}\}$показано на рисунке справа. Для солитонов более высокого порядка ($N>1\; \{\; \backslash \; displaystyle\; N>1\}$) мы можем использовать следующее выражение закрытой:

$a\; (\tau ,\; \zeta \; =\; 0)\; =\; N\; tanh\; \; (\tau ).\; \{\backslash \; Displaystyle\; а\; (\backslash \; тау,\; \backslash \; дзета\; =\; 0)\; =\; N\; \backslash \; танх\; (\backslash \; тау).\; \backslash \}$

Это солитон в том смысле, что он распространяется, не меняя своей формы, но не создается нормальный пульс; скорее, это недостаток энергии в непрерывном временном пучке. Интенсивность постоянна, но в течение короткого времени, в течение которого она скачет до нуля и обратно, генерируя «темный импульс» ». Эти солитоны фактически могут быть сгенерированы путем введения коротких темных импульсов в более стандартные импульсы. С темными солитонами труднее работать, чем со стандартными солитонами, но они показали, что они более устойчивы и устойчивы к потерям.

• Солитон
• Фазовая самомодуляция
• Оптический эффект Керра
• Трехмерный солитон
• нематикон
• Ультракороткий импульс

Викискладе есть материалы, связанные с Солитонами (оптика).

• Распространение солитонов в SMF-28 с использованием GPU