Нормально распределенные и некоррелированные не подразумевают независимость

В теории вероятностей, хотя простые примеры показывают, что линейная некоррелированность двух случайных величин, как правило, не подразумевает их независимость, иногда ошибочно полагают, что когда две случайные величины нормально распределены. Эта статья демонстрирует, что предположение о нормальном распределении не имеет таких последствий, хотя многомерное нормальное распределение , включая двумерное нормальное распределение, имеет.

Сказать, что пара $(X,\; Y)\; \{\backslash \; displaystyle\; (X,\; Y)\}$случайных величин имеет двумерное нормальное распределение, означает, что каждая линейная комбинация $a\; X\; +\; b\; Y\; \{\backslash \; displaystyle\; aX\; +\; bY\}$из $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$для постоянных (то есть не случайных) коэффициентов $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$имеет одномерное нормальное распределение. В этом случае, если $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$не коррелированы, то они независимы. Однако две случайные величины $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$могут быть распределены вместе так, что каждая из них по отдельности незначительно нормально распределены, и они некоррелированы, но не независимы; примеры приведены ниже.

• 1 Примеры
  • 1.1 Симметричный пример
  • 1.2 Асимметричный пример
  • 1.3 Примеры с поддержкой почти везде в ℝ
• 2 См. Также
• 3 Ссылки

Симметричный пример

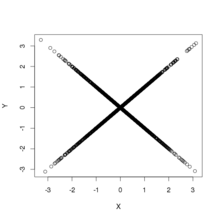
Объединенный диапазон $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$. Темнее означает более высокое значение функции плотности.

Предположим, что $X\; \{\backslash \; displaystyle\; X\}$имеет нормальное распределение с ожидаемым значением 0 и дисперсией 1. Пусть $W\; \{\backslash \; displaystyle\; W\}$имеют распределение Радемахера, так что $W\; =\; 1\; \{\backslash \; displaystyle\; W\; =\; 1\}$или $W\; =\; -\; 1\; \{\backslash \; displaystyle\; W\; =\; -1\}$, каждое с вероятностью 1/2, и предположим, что $W\; \{\backslash \; displaystyle\; W\}$не зависит от $X\; \{\backslash \; стиль\; отображения\; X\}$. Пусть $Y\; =\; W\; X\; \{\backslash \; displaystyle\; Y\; =\; WX\}$. Тогда

• $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$не коррелированы;
• оба имеют одинаковое нормальное распределение; и
• $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$не являются независимыми.

Чтобы увидеть, что $X\; \{\backslash \; displaystyle\; X\; \}$и $Y\; \{\backslash \; displaystyle\; Y\}$не коррелированы, можно принять во внимание ковариацию $cov\; \; (X,\; Y)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{cov\}\; (X,\; Y)\}$: по определению это

$cov\; \; (X,\; Y)\; =\; E\; \; (XY)\; -\; E\; \; (X)\; E\; \; (Y).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{cov\}\; (X,\; Y)\; =\; \backslash \; operatorname\; \{E\}\; (XY)\; -\; \backslash \; operatorname\; \{E\}\; (X)\; \backslash \; operatorname\; \{E\}\; (Y).\}$

Тогда по определению случайного переменные $X\; \{\backslash \; displaystyle\; X\}$, $Y\; \{\backslash \; displaystyle\; Y\}$и $W\; \{\backslash \; displaystyle\; W\}$, а также независимость $W\; \{\backslash \; displaystyle\; W\}$из $X\; \{\backslash \; displaystyle\; X\}$, один имеет

$cov\; \; (X,\; Y)\; =\; E\; \; (XY)\; -\; 0\; =\; E\; \; (Икс\; 2\; W)\; знак\; равно\; E\; \; (X\; 2)\; E\; \; (W)\; =\; E\; \; (X\; 2)\; \cdot \; 0\; =\; 0.\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{cov\}\; (X,\; Y)\; =\; \backslash \; OperatorName\; \{E\}\; (XY)\; -0\; =\; \backslash \; operatorname\; \{E\}\; (X\; ^\; \{2\}\; W)\; =\; \backslash \; operatorname\; \{E\}\; (X\; ^\; \{2\})\; \backslash \; operatorname\; \{E\}\; (W)\; =\; \backslash \; operatorname\; \{E\}\; (X\; ^\; \{\; 2\})\; \backslash \; cdot\; 0\; =\; 0.\}$

Чтобы увидеть, что $Y\; \{\backslash \; displaystyle\; Y\}$имеет то же нормальное распределение, что и $X\; \{\backslash \; displaystyle\; X\}$, рассмотрим

$Pr\; (Y\; \le \; x)\; =\; E\; \; (Pr\; (Y\; \le \; x\; \mid \; W))\; =\; Pr\; (X\; \le \; x)\; Pr\; (W\; =\; 1)\; +\; Pr\; (-\; X\; \le \; x)\; Pr\; (W\; Знак\; равно\; -\; 1)\; знак\; равно\; \Phi \; (Икс)\; \cdot \; 1\; 2\; +\; \Phi \; (Икс)\; \cdot \; 1\; 2\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Pr\; (Y\; \backslash \; Leq\; x)\; \{\}\; =\; \backslash \; operatorname\; \{E\}\; (\backslash \; Pr\; (\; Y\; \backslash \; leq\; x\; \backslash \; mid\; W))\; \backslash \backslash \; \{\; \}\; =\; \backslash \; Pr\; (X\; \backslash \; leq\; x)\; \backslash \; Pr\; (W\; =\; 1)\; +\; \backslash \; Pr\; (-X\; \backslash \; leq\; x)\; \backslash \; Pr\; (W\; =\; -1)\; \backslash \backslash \; \{\}\; =\; \backslash \; Phi\; (x)\; \backslash \; cdot\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; +\; \backslash \; Phi\; (x)\; \backslash \; cdot\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; end\; \{align\}\}\}$

(поскольку $X\; \{\backslash \; displaystyle\; X\}$и $-\; X\; \{\backslash \; displaystyle\; -X\}$оба имеют одинаковое нормальное распределение), где $\Phi \; (x)\; \{\backslash \; displaystyle\; \backslash \; Phi\; (x)\}$- это кумулятивная функция распределения нормального распределения.

Чтобы увидеть, что $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$не являются независимыми, обратите внимание, что $|\; Y\; |\; =\; |\; X\; |\; \{\backslash \; displaystyle\; |\; Y\; |\; =\; |\; X\; |\}$или что $Pr\; \; (Y>1\; |\; X\; =\; 1/2)\; =\; Pr\; \; (X>1\; |\; X\; =\; 1/2)\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Pr\}\; (Y>1\; |\; X\; =\; 1/2)\; =\; \backslash \; operatorname\; \{Pr\}\; (X>1\; |\; X\; =\; 1/2)\; =\; 0\}$.

Наконец, распределение простой линейной комбинации $X\; +\; Y\; \{\backslash \; displaystyle\; X\; +\; Y\}$концентрирует положительную вероятность в 0: $Pr\; \; (X\; +\; Y\; =\; 0)\; =\; 1/2\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Pr\}\; (X\; +\; Y\; =\; 0)\; =\; 1/2\}$. Следовательно случайная величина $X\; +\; Y\; \{\backslash \; displaystyle\; X\; +\; Y\}$не имеет нормального распределения, а также $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$совместно не распределены нормально (по определению выше).

Пример асимметрии

Совместная плотность $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$. Da rker указывает более высокое значение плотности.

Предположим, что $X\; \{\backslash \; displaystyle\; X\}$имеет нормальное распределение с ожидаемым значением 0 и дисперсией 1. Пусть

$Y\; =\; \{X,\; если\; |\; X\; |\; \le \; c\; -\; X,\; если\; |\; X\; |>с\; \{\backslash \; displaystyle\; Y\; =\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{matrix\}\; X\; \{\backslash \; text\; \{if\}\}\; \backslash \; left\; |\; X\; \backslash \; right\; |\; \backslash \; leq\; c\; \backslash \backslash \; -\; X\; \{\backslash \; text\; \{if\}\}\; \backslash \; left\; |\; X\; \backslash \; right\; |>c\; \backslash \; end\; \{matrix\}\}\; \backslash \; right.\}$

где $c\; \{\backslash \; displaystyle\; c\}$- положительное число, которое необходимо указать ниже. $c\; \{\backslash \; displaystyle\; c\}$очень мало, тогда correlation $corr\; \; (X,\; Y)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{corr\}\; (X,\; Y)\}$находится рядом с $-\; 1\; \{\backslash \; displaystyle\; -1\}$, если $c\; \{\backslash \; displaystyle\; c\}$очень большой, то $corr\; \; (X,\; Y)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{corr\}\; (X,\; Y)\}$близко к 1. Поскольку корреляция является непрерывной функцией от $c\; \{\backslash \; displaystyle\; c\}$, теорема о промежуточном значении предполагает, что существует какое-то конкретное значение $c\; \{\backslash \; displaystyle\; c\}$, которое делает корреляцию 0. Это значение примерно маты 1.54. В этом случае $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$некоррелированы, но они явно не независимы, поскольку $X\; \{\backslash \; displaystyle\; X\}$полностью определяет $Y\; \{\backslash \; displaystyle\; Y\}$.

. Чтобы увидеть, что $Y\; \{\backslash \; displaystyle\; Y\}$нормально распределен - действительно, его распределение совпадает с распределением $X\; \{\backslash \; displaystyle\; X\}$- можно вычислить его кумулятивную функцию распределения :

$Pr\; (Y\; \le \; x)\; =\; Pr\; (\{|\; X\; |\; \le \; c\; и\; X\; \le \; x\}\; или\; \{|\; X\; |>c\; и\; -\; X\; \le \; x\})\; =\; Pr\; (|\; X\; |\; \le \; c\; и\; X\; \le \; x)\; +\; Pr\; (|\; X\; |>c\; и\; -\; X\; \le \; x)\; =\; Pr\; (|\; Икс\; |\; \le \; c\; и\; X\; \le \; x)\; +\; Pr\; (|\; X\; |>c\; и\; X\; \le \; x)\; =\; Pr\; (X\; \le \; x),\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Pr\; (Y\; \backslash \; Leq\; x)\; =\; \backslash \; Pr\; (\backslash \; \{|\; X\; |\; \backslash \; leq\; c\; \{\backslash \; text\; \{and\}\}\; X\; \backslash \; leq\; x\; \backslash \}\; \{\backslash \; text\; \{или\}\}\; \backslash \; \{|\; X\; |>c\; \{\backslash \; text\; \{and\}\}\; -\; X\; \backslash \; leq\; x\; \backslash \})\; \backslash \backslash \; =\; \backslash \; Pr\; (|\; X\; |\; \backslash \; leq\; c\; \{\backslash \; text\; \{and\}\}\; X\; \backslash \; leq\; x)\; +\; \backslash \; Pr\; (|\; X\; |>c\; \{\backslash \; text\; \{and\}\}\; -\; X\; \backslash \; leq\; x)\; \backslash \backslash \; =\; \backslash \; Pr\; (|\; X\; |\; \backslash \; leq\; c\; \{\backslash \; text\; \{and\}\}\; X\; \backslash \; leq\; x)\; +\; \backslash \; Pr\; (|\; X\; |>c\; \{\backslash \; text\; \{and\}\}\; X\; \backslash \; leq\; x)\; \backslash \backslash \; =\; \backslash \; Pr\; (X\; \backslash \; leq\; x),\; \backslash \; end\; \{align\}\}\}$

где предпоследнее равенство следует из симметрии распределения $X\; \{\backslash \; displaystyle\; X\}$и симметрии условия, что $|\; X\; |\; \le \; c\; \{\backslash \; displaystyle\; |\; X\; |\; \backslash \; leq\; c\}$.

В этом примере разница $X\; -\; Y\; \{\backslash \; displaystyle\; XY\}$далека от нормального распределения, поскольку имеет существенное вероятность (около 0,88) того, что она равна 0. Напротив, нормальное распределение, будучи непрерывным распределением, не имеет дискретной части, то есть не концентрирует больше, чем нулевую вероятность в любой отдельной точке. Следовательно, $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$не являются совместно нормально распределенными, хотя они обычно распределены по отдельности.

Примеры с поддержкой почти везде в ℝ

Хорошо известно, что соотношение $C\; \{\backslash \; displaystyle\; C\}$двух независимых стандартных нормальных случайных отклонений $X\; i\; \{\backslash \; displaystyle\; X\_\; \{i\}\}$и $Y\; i\; \{\backslash \; displaystyle\; Y\_\; \{i\}\}$имеет распределение Коши. С таким же успехом можно начать со случайной величины Коши $C\; \{\backslash \; displaystyle\; C\}$и получить условное распределение $Y\; i\; \{\backslash \; displaystyle\; Y\_\; \{i\}\}$чтобы удовлетворить требованию, чтобы $X\; i\; =\; CY\; i\; \{\backslash \; displaystyle\; X\_\; \{i\}\; =\; CY\_\; \{i\}\}$с $X\; i\; \{\backslash \; displaystyle\; X\_\; \{i\}\}$и $Y\; i\; \{\backslash \; displaystyle\; Y\_\; \{i\}\}$независимый и стандартный нормальный. Просчитывая математику, обнаруживаем, что

$Y\; i\; =\; W\; i\; \chi \; i\; 2\; (k\; =\; 2)\; 1\; +\; C\; 2\; \{\backslash \; displaystyle\; Y\_\; \{i\}\; =\; W\_\; \{i\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; chi\; \_\; \{\; i\}\; ^\; \{2\}\; \backslash \; left\; (k\; =\; 2\; \backslash \; right)\}\; \{1\; +\; C\; ^\; \{2\}\}\}\}\}$

где $W\; i\; \{\backslash \; displaystyle\; W\_\; \{i\}\}$- случайная величина Радемахера, а $\chi \; i\; 2\; (k\; =\; 2)\; \{\backslash \; displaystyle\; \backslash \; chi\; \_\; \{i\}\; ^\; \{2\}\; \backslash \; left\; (k\; =\; 2\; \backslash \; right)\}$- Хи-квадрат случайная величина с двумя степенями свободы.

Рассмотрим два набора $(X\; i,\; Y\; i)\; \{\backslash \; displaystyle\; \backslash \; left\; (X\_\; \{i\},\; Y\_\; \{i\}\; \backslash \; right)\}$, $i\; \in \; \{1,\; 2\}\; \{\; \backslash \; Displaystyle\; i\; \backslash \; in\; \backslash \; left\; \backslash \; \{1,2\; \backslash \; right\; \backslash \}\}$. Обратите внимание, что $C\; \{\backslash \; displaystyle\; C\}$не индексируется $i\; \{\backslash \; displaystyle\; i\}$- то есть той же случайной величиной Коши $C\; \{\; \backslash \; displaystyle\; C\}$используется в определении как $(X\; 1,\; Y\; 1)\; \{\backslash \; displaystyle\; \backslash \; left\; (X\_\; \{1\},\; Y\_\; \{1\}\; \backslash \; right)\}$и $(X\; 2,\; Y\; 2)\; \{\backslash \; displaystyle\; \backslash \; left\; (X\_\; \{2\},\; Y\_\; \{2\}\; \backslash \; right)\}$. Это совместное использование $C\; \{\backslash \; displaystyle\; C\}$приводит к зависимостям между индексами: ни $X\; 1\; \{\backslash \; displaystyle\; X\_\; \{1\}\}$, ни $Y\; 1\; \{\backslash \; displaystyle\; Y\_\; \{1\}\}$не зависит от $Y\; 2\; \{\backslash \; displaystyle\; Y\_\; \{2\}\}$. Тем не менее, все $X\; i\; \{\backslash \; displaystyle\; X\_\; \{i\}\}$и $Y\; i\; \{\backslash \; displaystyle\; Y\_\; \{i\}\}$не коррелированы, поскольку все двумерные распределения имеют симметрию отражения по осям.

Ненормальные совместные распределения с нормальными краями.

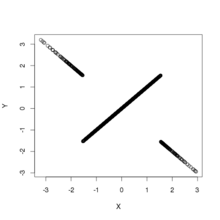
На рисунке показаны диаграммы рассеяния выборок, взятых из вышеуказанного распределения. Это дает два примера двумерных распределений, которые некоррелированы и имеют нормальные предельные распределения, но не являются независимыми. На левой панели показано совместное распределение $X\; 1\; \{\backslash \; displaystyle\; X\_\; \{1\}\}$и $Y\; 2\; \{\backslash \; displaystyle\; Y\_\; \{2\}\}$; дистрибутив поддерживается везде, но не у истоков. На правой панели показано совместное распределение $Y\; 1\; \{\backslash \; displaystyle\; Y\_\; \{1\}\}$и $Y\; 2\; \{\backslash \; displaystyle\; Y\_\; \{2\}\}$; распределение имеет поддержку везде, кроме осей, и имеет разрыв в начале координат: плотность расходится при приближении к началу координат по любому прямому пути, кроме осей.

• Корреляция и зависимость