дерево kd - k-d tree

редактировать

Многомерное дерево поиска точек в k-мерном пространстве

дерево kd

Тип

Многомерное BST

Изобретено

1975

Изобретено

Джоном Луисом Бентли

Сложность времени в нотации Big O

Алгоритм	Среднее	Худший случай
Пробел	$O (n) {\ displaystyle O (n)}$ $O (n)$	$O (n) {\ displaystyle O (n)}$ $O (n)$
Search	$O (log ⁡ n) {\ displaystyle O (\ log n)}$ $O (\ log n)$	$O (n) {\ displaystyle O (n)}$ $O (n)$
Insert	$O (log ⁡ n) {\ displaystyle O (\ log n)}$ $O (\ log n)$	$O (n) {\ displaystyle O (n)}$ $O (n)$
Удалить	$O (log ⁡ n) {\ displaystyle O (\ log n)}$ $O (\ log n)$	$O (n) {\ displaystyle O (n)}$ $O (n)$

Трехмерное дерево kd. Первое разделение (красная вертикальная плоскость) разрезает корневую ячейку (белая) на две части, каждая из которых затем разделяется (зелеными горизонтальными плоскостями) на две части. Наконец, четыре ячейки разделяются (четырьмя синими вертикальными плоскостями) на две части. Поскольку больше нет разделения, последние восемь называются листовыми ячейками.

В информатике, kd-дерево (сокращение от k-мерного дерева ) представляет собой разбиение на пространства структуру данных для организации точек в k-мерном пространстве. Деревья k-d представляют собой полезную структуру данных для нескольких приложений, таких как поиск с использованием многомерного ключа поиска (например, поиск по диапазону и поиск по ближайшему соседу ). k-d деревья являются частным случаем деревьев разбиения двоичного пространства.

Содержание

1 Неформальное описание
2 Операции над деревьями kd
- 2.1 Конструкция
- 2.2 Добавление элементов
- 2.3 Удаление элементов
- 2.4 Балансировка
- 2.5 Поиск ближайшего соседа
- 2.6 Поиск по диапазону
3 Снижение производительности с данными большого размера
4 Снижение производительности, когда точка запроса находится далеко от точек в дереве kd
5 Сложность
6 Варианты
- 6.1 Объемные объекты
- 6.2 Точки только в листьях
7 См. Также
8 Реализации с открытым исходным кодом
9 Ссылки

Неформальное описание

Дерево kd - это двоичное дерево в котором каждый листовой узел является k-мерной точкой. Каждый нелистовой узел можно рассматривать как неявно генерирующий разделение гиперплоскости, которая делит пространство на две части, известные как полупространства. Точки слева от этой гиперплоскости представлены левым поддеревом этого узла, а точки справа от гиперплоскости представлены правым поддеревом. Направление гиперплоскости выбирается следующим образом: каждый узел в дереве связан с одним из k измерений, причем гиперплоскость перпендикулярна оси этого измерения. Так, например, если для определенного разделения выбрана ось «x», все точки в поддереве с меньшим значением «x», чем узел, появятся в левом поддереве, а все точки с большим значением «x» будут в правом поддереве. В таком случае гиперплоскость будет задаваться значением x точки, а ее нормал будет единицей оси x.

Операции с деревьями kd

Построение

Поскольку существует много возможных способов выбора плоскостей разделения, выровненных по оси, существует много различных способов построения деревьев kd. Канонический метод построения k-d дерева имеет следующие ограничения:

При движении вниз по дереву он циклически перемещается по осям, используемым для выбора плоскостей разделения. (Например, в трехмерном дереве корень будет иметь плоскость, выровненную по оси x, дочерние элементы корня будут иметь плоскости, выровненные по оси y, все внуки корня будут иметь плоскости, выровненные по оси z, все правнуки корня будут имеют плоскости, выровненные по оси x, все праправнуки корня будут иметь плоскости, выровненные по оси y, и т. д.)
Точки вставляются путем выбора медианы помещаемых точек в поддерево относительно их координат на оси, используемой для создания плоскости разделения. (Обратите внимание на предположение, что мы передаем весь набор из n точек в алгоритм заранее.)

Этот метод приводит к сбалансированному дереву kd, в котором каждый листовой узел находится примерно на одинаковом расстоянии от корень. Однако сбалансированные деревья не обязательно оптимальны для всех приложений.

Обратите внимание, что выбирать среднюю точку не требуется. В случае, если средние точки не выбраны, нет гарантии, что дерево будет сбалансировано. Чтобы избежать кодирования сложного алгоритма O (n) median-finding или использования сортировки O (n log n), например heapsort или mergesort для сортировки всех n точек, популярной практикой является сортировка фиксированного числа случайно выбранных точек и использование медианы этих точек в качестве плоскости разделения. На практике этот метод часто приводит к хорошо сбалансированным деревьям.

Учитывая список из n точек, следующий алгоритм использует сортировку с нахождением медианы для построения сбалансированного k-d дерева, содержащего эти точки.

function kdtree (список точек pointList, int depth) {// Выбор оси на основе глубины, чтобы ось циклически проходила через все допустимые значения var int axis: = depth mod к; // Список точек сортировки и выбрать в качестве поворотного медианный элемента выберите средний по оси от PointList; // Создать узел и построить поддерево node.location: = median; node.leftChild: = kdtree (точки в pointList до медианы, глубина + 1); node.rightChild: = kdtree (точки в pointList после медианы, глубина + 1); вернуть узел; }

Обычно точки «после» медианы включают только те, которые строго больше медианы. Для точек, лежащих на медиане, можно определить "суперключевую" функцию, которая сравнивает точки во всех измерениях. В некоторых случаях допустимо, чтобы точки, равные медиане, лежали по одну сторону от медианы, например, путем разделения точек на подмножество «меньше чем» и подмножество «больше или равно».

Пример реализации
Вышеупомянутый алгоритм, реализованный на языке программирования Python, выглядит следующим образом: из коллекций import namedtuple из оператора import itemgetter из pprint import pformat class Node (namedtuple ('Node', 'location left_child right_child')): def __repr __ (self): return pformat (tuple (self)) def kdtree (point_list, depth: int = 0): if not point_list: return None k = len (point_list [0]) # предполагается, что все точки имеют одинаковый размер # Выберите ось на основе глубины, чтобы ось циклически проходила по всем допустимым значениям axis = depth% k # Сортировать список точек по оси и выбрать медиану в качестве элемента поворота point_list.sort (key = itemgetter (axis)) median = len (point_list) // 2 # Создать узел и построить поддеревья return Node (location = point_list [median], left_child = kdtree (point_list [: median], depth + 1), right_child = kdtree (point_list [median + 1: ], depth + 1)) def main (): "" "Пример использования" "" point_list = [(7,2), (5,4), (9,6), (4,7), (8, 1), (2,3)] tree = kdtree (point_list) pri nt (tree) if __name__ == '__main__': main () Результат будет: ((7, 2), ((5, 4), ((2, 3), None, None), ((4, 7), None, None)), ((9, 6), ((8, 1), None, None), None)) Сгенерированное дерево показано ниже. 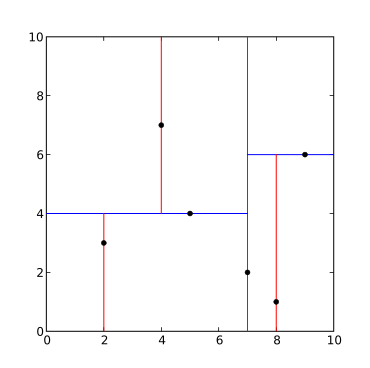разложение дерева kd для набора точек. `(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)`. Результирующее дерево kd.

Вышеупомянутый алгоритм, реализованный на языке программирования Python, выглядит следующим образом:

из коллекций import namedtuple из оператора import itemgetter из pprint import pformat class Node (namedtuple ('Node', 'location left_child right_child')): def __repr __ (self): return pformat (tuple (self)) def kdtree (point_list, depth: int = 0): if not point_list: return None k = len (point_list [0]) # предполагается, что все точки имеют одинаковый размер # Выберите ось на основе глубины, чтобы ось циклически проходила по всем допустимым значениям axis = depth% k # Сортировать список точек по оси и выбрать медиану в качестве элемента поворота point_list.sort (key = itemgetter (axis)) median = len (point_list) // 2 # Создать узел и построить поддеревья return Node (location = point_list [median], left_child = kdtree (point_list [: median], depth + 1), right_child = kdtree (point_list [median + 1: ], depth + 1)) def main (): "" "Пример использования" "" point_list = [(7,2), (5,4), (9,6), (4,7), (8, 1), (2,3)] tree = kdtree (point_list) pri nt (tree) if __name__ == '__main__': main ()

Результат будет:

((7, 2), ((5, 4), ((2, 3), None, None), ((4, 7), None, None)), ((9, 6), ((8, 1), None, None), None))

Сгенерированное дерево показано ниже.

разложение дерева kd для набора точек. (2,3), (5,4), (9,6), (4,7), (8,1), (7,2).

Результирующее дерево kd.

Этот алгоритм создает инвариант, согласно которому для любого узла все узлы в левом поддереве находятся на одной стороне разбиения plane, а все узлы в правом поддереве находятся на другой стороне. Точки, лежащие в плоскости разделения, могут появиться с обеих сторон. Плоскость разделения узла проходит через точку, связанную с этим узлом (в коде обозначается как node.location).

Альтернативные алгоритмы построения сбалансированного k-d дерева предварительно сортируют данные перед построением дерева. Затем они поддерживают порядок предварительной сортировки во время построения дерева и, следовательно, исключают дорогостоящий этап поиска медианы на каждом уровне подразделения. Два таких алгоритма строят сбалансированное k-d дерево для сортировки треугольников, чтобы улучшить время выполнения трассировки лучей для трехмерной компьютерной графики. Эти алгоритмы предварительно сортируют n треугольников перед построением k-d дерева, а затем строят дерево за O (n log n) времени в лучшем случае. Алгоритм, который строит сбалансированное k-d дерево для сортировки точек, имеет сложность наихудшего случая O (kn log n). Этот алгоритм преобразует n точек в каждом из k измерений с использованием сортировки O (n log n), такой как Heapsort или Mergesort, до построения дерева. Затем он поддерживает порядок этих k предварительных сортировок во время построения дерева и, таким образом, избегает нахождения медианы на каждом уровне подразделения.

Добавление элементов

Добавляют новую точку в k-d дерево так же, как добавляют элемент в любое другое дерево поиска. Сначала обойдите дерево, начиная от корня и двигаясь либо к левому, либо к правому дочернему элементу, в зависимости от того, находится ли вставляемая точка «слева» или «справа» от плоскости разделения. Как только вы дойдете до узла, под которым должен располагаться дочерний элемент, добавьте новую точку как левый или правый дочерний элемент листового узла, опять же, в зависимости от того, на какой стороне плоскости разделения узла находится новый узел.

Добавление точек таким образом может привести к разбалансировке дерева, что приведет к снижению производительности дерева. Скорость снижения производительности дерева зависит от пространственного распределения добавляемых точек дерева и количества добавляемых точек по отношению к размеру дерева. Если дерево становится слишком несбалансированным, может потребоваться повторная балансировка для восстановления производительности запросов, основанных на балансировке дерева, таких как поиск ближайшего соседа.

Удаление элементов

Чтобы удалить точку из существующего kd-дерева, не нарушая инварианта, самый простой способ - сформировать набор всех узлов и листьев из дочерних узлов целевого узла, и воссоздайте эту часть дерева.

Другой подход - найти замену удаленной точке. Сначала найдите узел R, содержащий точку, которую нужно удалить. Для базового случая, когда R - листовой узел, замена не требуется. В общем случае найдите точку замены, скажем p, из поддерева с корнем R. Замените точку, хранящуюся в R, на p. Затем рекурсивно удалите p.

Для поиска точки замены, если R различает x (скажем) и у R есть правильный дочерний элемент, найдите точку с минимальным значением x из поддерева, имеющего корень в правом дочернем элементе. В противном случае найдите точку с максимальным значением x из поддерева с корнем слева.

Балансировка

Балансировка дерева kd требует осторожности, потому что деревья kd отсортированы по нескольким измерениям, поэтому метод поворота дерева нельзя использовать для их балансировки, так как это может нарушить инвариант.

Существует несколько вариантов сбалансированных k-d деревьев. Они включают разделенное дерево k-d, псевдо-k-d дерево, K-D-B-tree, hB-tree и Bkd-tree. Многие из этих вариантов являются адаптивными k-d деревьями.

Поиск ближайшего соседа

Воспроизвести медиа Пример поиска ближайшего соседа в двумерном дереве. Здесь дерево уже построено, каждый узел соответствует прямоугольнику, каждый прямоугольник разделен на два равных подпрямоугольника, а листья соответствуют прямоугольникам, содержащим одну точку

Алгоритм поиска ближайшего соседа (NN) стремится найти точку в дереве, ближайшую к заданной входной точке. Этот поиск можно выполнять эффективно, используя свойства дерева, чтобы быстро исключить большие части пространства поиска.

Поиск ближайшего соседа в дереве kd происходит следующим образом:

Начиная с корневого узла, алгоритм рекурсивно перемещается вниз по дереву, так же, как если бы точка поиска была вставлена (т.е. он идет влево или вправо в зависимости от того, больше или меньше точка текущего узла в разделенном измерении).
Как только алгоритм достигает листового узла, он проверяет эту узловую точку и если расстояние лучше, эта узловая точка сохраняется как "текущая лучшая".
Алгоритм разворачивает рекурсию дерева, выполняя следующие шаги на каждом узле:
1. Если текущий узел ближе чем текущий лучший, тогда он становится лучшим на текущий момент.
2. Алгоритм проверяет, могут ли быть какие-либо точки на другой стороне плоскости разделения, которые ближе к точке поиска, чем текущее лучшее. По идее, это делается путем пересечения разделяющей гиперплоскости с гиперсферой вокруг точки поиска, радиус которой равен текущему ближайшему расстоянию. Поскольку все гиперплоскости выровнены по осям, это реализовано как простое сравнение, чтобы увидеть, меньше ли расстояние между координатой разделения точки поиска и текущим узлом, чем расстояние (общие координаты) от точки поиска до текущей наилучшей точки.
  1. Если гиперсфера пересекает плоскость, на другой стороне плоскости могут быть более близкие точки, поэтому алгоритм должен двигаться вниз по другой ветви дерева от текущего узла в поисках более близких точек, следуя тем же рекурсивный процесс как весь поиск.
  2. Если гиперсфера не пересекает плоскость разделения, то алгоритм продолжает движение вверх по дереву, и вся ветвь на другой стороне этого узла удаляется.
Когда алгоритм завершает этот процесс для корневого узла, тогда поиск завершается.

Обычно алгоритм использует квадрат расстояний для сравнения, чтобы избежать вычисления квадратных корней. Кроме того, он может сэкономить вычисления, сохраняя квадрат текущего лучшего расстояния в переменной для сравнения.

С помощью простых модификаций алгоритм может быть расширен несколькими способами. Он может предоставить k ближайших соседей к точке, поддерживая k текущих рекордов вместо одного. Ветвь удаляется только тогда, когда найдено k точек, и ветвь не может иметь точек ближе, чем любая из текущих вершин k.

Его также можно преобразовать в алгоритм приближения, чтобы он работал быстрее. Например, приблизительный поиск ближайшего соседа может быть достигнут путем простой установки верхней границы количества точек для исследования в дереве или путем прерывания процесса поиска на основе часов реального времени (что может быть более подходящим в аппаратных реализациях). Ближайший сосед для точек, которые уже находятся в дереве, может быть достигнут, не обновляя уточнение для узлов, которые дают нулевое расстояние в результате, это имеет обратную сторону отбрасывания точек, которые не уникальны, но совмещены с исходной точкой поиска.

Приблизительный ближайший сосед полезен в приложениях реального времени, таких как робототехника, из-за значительного увеличения скорости, получаемого за счет отсутствия исчерпывающего поиска наилучшей точки. Одна из его реализаций - поиск по диапазону поиска.

поиск по диапазону

Поиск по диапазону ищет диапазоны параметров. Например, если дерево хранит значения, соответствующие доходу и возрасту, то поиск по диапазону может быть чем-то вроде поиска всех членов дерева, которые имеют возраст от 20 до 50 лет и доход от 50 000 до 80 000. Поскольку k-d деревья делят диапазон домена пополам на каждом уровне дерева, они полезны для выполнения поиска по диапазону.

Анализ деревьев двоичного поиска показал, что время наихудшего случая для поиска по диапазону в k-мерном дереве kd, содержащем n узлов, определяется следующим уравнением.

t наихудший = O (k ⋅ n 1 - 1 k) {\ displaystyle t _ {\ text {худший}} = O (k \ cdot n ^ {1 - {\ frac {1} {k}}})}

{\ displaystyle t _ {\ text {худший}} = O (k \ cdot n ^ {1 - {\ frac {1} {k}}})}

Снижение производительности при работе с данными большого размера

Поиск ближайшей точки - это операция O (log n) в среднем в случае случайно распределенных точек, хотя анализ в целом сложен.

В высоком -мерных пространств, проклятие размерности заставляет алгоритм посещать гораздо больше ветвей, чем в пространствах меньшей размерности. В частности, когда количество точек лишь немного превышает количество измерений, алгоритм лишь немного лучше, чем линейный поиск всех точек. Как правило, если размерность $k {\ displaystyle k}$ $k$ , количество точек в данных $n {\ displaystyle n}$ $n$ должно быть $n ≫ 2 k {\ displaystyle n \ gg 2 ^ {k}}$ ${\ displaystyle n \ gg 2 ^ {k}}$ . В противном случае, когда деревья $k {\ displaystyle k}$ $k$ -d используются с многомерными данными, большинство точек в дереве будет оцениваться, и эффективность будет не лучше, чем при исчерпывающем поиске, и, если требуется достаточно хороший и быстрый ответ, следует использовать методы приближенного ближайшего соседа.

Снижение производительности, когда точка запроса находится далеко от точек в дереве kd

Кроме того, даже в низкоразмерном пространстве, если среднее попарное расстояние между k ближайшими соседями точки запроса значительно меньше, чем среднее расстояние между точкой запроса и каждым из k ближайших соседей, производительность поиска ближайшего соседа ухудшается в сторону линейной, поскольку расстояния от точки запроса до каждого ближайшего соседа имеют одинаковую величину. (В худшем случае рассмотрим облако точек, распределенное на поверхности сферы с центром в начале координат. Каждая точка равноудалена от начала координат, поэтому поиск ближайшего соседа из начала координат должен проходить по всем точкам на поверхность сферы для идентификации ближайшего соседа - который в данном случае даже не уникален.)

Чтобы смягчить потенциально значительное снижение производительности поиска по дереву kd в худшем случае, может быть предоставлен параметр максимального расстояния алгоритму поиска по дереву, и рекурсивный поиск может быть сокращен всякий раз, когда ближайшая точка в данной ветви дерева не может быть ближе, чем это максимальное расстояние. Это может привести к тому, что поиск ближайшего соседа не сможет вернуть ближайшего соседа, что означает, что никакие точки не находятся на этом максимальном расстоянии от точки запроса.

Сложность

Построение статического kd-дерева из n точек имеет следующую сложность наихудшего случая:
- O (n log n), если O (n log n) сортировать такой поскольку Heapsort или Mergesort используется для поиска медианы на каждом уровне зарождающегося дерева;
- O (n log n), если O (n) алгоритм медианы медианы используется для выбора медианы на каждом уровне зарождающегося дерева;
- O (kn log n), если n точек предварительно отсортированы в каждом из k измерений с использованием O (n log n) сортировка, такая как Heapsort или Mergesort перед построением дерева kd.
Для вставки новой точки в сбалансированное дерево kd требуется O (log n) времени.
Удаление точки из сбалансированного дерева kd занимает O (log n) времени.
Запрос диапазона параллельности осям в сбалансированном kd-дерево занимает O (n + m) времени, где m - количество зарегистрированных точек, а k - размерность kd-дерева.
Поиск 1 ближайшего соседа в сбалансированном kd дерево со случайно распределенной точкой s занимает в среднем O (log n) времени.

Варианты

Объемные объекты

Вместо точек дерево kd может также содержать прямоугольников или гипер прямоугольники. Таким образом, поиск по диапазону превращается в проблему возврата всех прямоугольников, пересекающих прямоугольник поиска. Дерево строится обычным образом со всеми прямоугольниками на листьях. В поиске ортогонального диапазона противоположная координата используется при сравнении с медианой. Например, если текущий уровень разделен по x high, мы проверяем координату x low прямоугольника поиска. Если медиана меньше, чем координата x low прямоугольника поиска, то никакой прямоугольник в левой ветви никогда не может пересекаться с прямоугольником поиска и поэтому может быть обрезан. В противном случае необходимо пройти обе ветви. См. Также дерево интервалов, которое является одномерным частным случаем.

Точки только в листьях

Также возможно определить k-d дерево с точками, хранящимися только в листьях. Эта форма k-d дерева позволяет использовать различные механики разделения, отличные от стандартного медианного разделения. Правило разделения средней точки выбирает середину самой длинной оси пространства, в котором производится поиск, независимо от распределения точек. Это гарантирует, что соотношение сторон будет не более 2: 1, но глубина зависит от распределения точек. Вариант, называемый скользящей средней точкой, разделяется только по середине, если есть точки по обе стороны от разделения. В противном случае он разделится на точку, ближайшую к середине. Маневонгватана и Маунт показывают, что это обеспечивает «достаточно хорошую» производительность на общих наборах данных.

Используя скользящую среднюю точку, на запрос приблизительного ближайшего соседа можно ответить в $O (1 ϵ d log ⁡ n) {\ displaystyle O \ left ({\ tfrac {1 } {{\ epsilon \} ^ {d}}} \ log n \ right)}$ ${\ displaystyle O \ left ({\ tfrac {1} {{\ epsi lon \} ^ {d}}} \ log n \ right)}$ . На приблизительный подсчет диапазона можно ответить в $O (log ⁡ n + (1 ϵ) d) {\ displaystyle O \ left (\ log n + {\ left ({\ tfrac {1} {\ epsilon \}} \ right)} ^ {d} \ right)}$ ${\ displaystyle O \ left (\ log n + {\ left ({\ tfrac {1} {\ epsilon \}} \ right)} ^ {d} \ right)}$ этим методом.

См. Также

Близкие варианты:

неявное дерево kd, дерево kd, определенное неявной функцией разделения, а не явно сохраненным набором разделений
min / max kd tree, дерево kd, которое связывает минимальное и максимальное значение с каждым из его узлов
расслабленное дерево kd, дерево kd, в котором дискриминанты в каждом узле являются произвольными

Связанные варианты:

Quadtree, структура разделения пространства, которая одновременно разделяется на два измерения, так что каждый узел имеет 4 дочерних элемента
Octree, структуру разделения пространства, которая одновременно разделяется в трех измерениях, так что каждый узел имеет 8 дочерних элементов
Ball tree, многомерное пространственное разбиение, полезное для поиска ближайшего соседа
R-tree и иерархия ограничивающих интервалов, структура для разделения объектов, а не точек, с перекрывающимися областями
дерево точек обзора, вариант kd-дерева, в котором для разделения da используются гиперсферы вместо гиперплоскостей. ta

Проблемы, которые могут быть решены с помощью деревьев kd:

Рекурсивное разбиение, метод построения деревьев статистических решений, похожих на деревья kd
проблема меры Кли, проблема вычисления площадь объединения прямоугольников, решаемая с помощью деревьев kd
Задача гильотины, проблема поиска дерева kd, ячейки которого достаточно велики, чтобы содержать заданный набор прямоугольников

Реализации с открытым исходным кодом

ALGLIB имеет реализации на C # и C ++ алгоритмов поиска ближайшего соседа на основе дерева kd и приблизительного ближайшего соседа.
SciPy, библиотека Python для научных вычислений, содержит реализации алгоритмов поиска ближайшего соседа на основе дерева kd.
scikit-learn, библиотека Python для машинного обучения, содержит реализации деревьев kd для поиска ближайших соседей и соседей по радиусу.

Ссылки