Многочлены Гегенбауэра

В математике, полиномы Гегенбауэра или ультрасферические полиномы C. n(x) равны ортогональные многочлены на интервале [−1,1] относительно весовой функции (1 - x). Они обобщают полиномы Лежандра и полиномы Чебышева и являются частными случаями полиномов Якоби. Они названы в честь Леопольда Гегенбауэра.

• 1 Характеристики
• 2 Ортогональность и нормализация
• 3 Приложения
• 4 См. Также
• 5 Ссылки

• 

  Многочлены Гегенбауэра с α = 1

• 

  многочленами Гегенбауэра с α = 2

• 

  многочленами Гегенбауэра с α = 3

• 

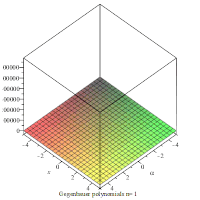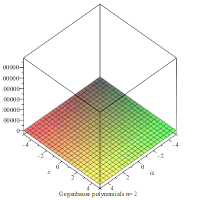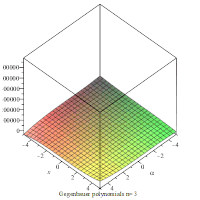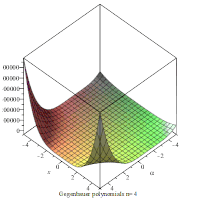
  Анимация, показывающая многочлены на плоскости xα для первых 4 значений n.

Доступны различные характеристики полиномов Гегенбауэра.

• Многочлены могут быть определены в терминах их производящей функции (Stein Weiss 1971, §IV.2):

$1\; (1-2\; xt\; +\; t\; 2)\; \alpha \; =\; \sum \; n\; =\; 0\; \infty \; C\; n\; (\alpha )\; (x)\; tn.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{(1-2xt\; +\; t\; ^\; \{2\})\; ^\; \{\backslash \; alpha\}\}\}\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; C\_\; \{n\}\; ^\; \{(\backslash \; alpha)\}\; (x)\; t\; ^\; \{n\}.\}$

• Многочлены удовлетворяют рекуррентному соотношению (Суетин 2001):

$C\; 0\; \alpha \; (x)\; =\; 1\; C\; 1\; \alpha \; (x)\; =\; 2\; \alpha \; x\; C\; n\; \alpha \; (x)\; =\; 1\; n\; [2\; x\; (n\; +\; \alpha \; -\; 1)\; C\; n\; -\; 1\; \alpha \; (x)\; -\; (n\; +\; 2\; \alpha \; -\; 2)\; C\; n\; -\; 2\; \alpha \; (x)].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; C\_\; \{0\}\; ^\; \{\backslash \; alpha\}\; (x)\; =\; 1\; \backslash \backslash \; C\_\; \{1\}\; ^\; \{\backslash \; alpha\}\; (x)\; =\; 2\; \backslash \; alpha\; x\; \backslash \backslash \; C\_\; \{n\; \}\; ^\; \{\backslash \; alpha\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; [2x\; (n\; +\; \backslash \; alpha\; -1)\; C\_\; \{n-1\}\; ^\; \{\backslash \; alpha\}\; (x)\; -\; (n\; +\; 2\; \backslash \; альфа\; -2)\; C\_\; \{n-2\}\; ^\; \{\backslash \; alpha\}\; (x)].\; \backslash \; end\; \{align\}\}\}$

• Многочлены Гегенбауэра являются частными решениями дифференциального уравнения Гегенбауэра (Суетин 2001):

$(\; 1\; -\; Икс\; 2)\; Y\; ″\; -\; (2\; \alpha \; +\; 1)\; xy\; \prime \; +\; n\; (n\; +\; 2\; \alpha )\; y\; =\; 0.\; \{\backslash \; displaystyle\; (1-x\; ^\; \{2\})\; y\; \text{'}\text{'}\; -\; (2\; \backslash \; alpha\; +1)\; xy\; \text{'}+\; n\; (n\; +\; 2\; \backslash \; alpha)\; y\; =\; 0.\; \backslash ,\}$

Когда α = 1/2, уравнение сводится к уравнению Лежандра, а полиномы Гегенбауэра сводятся к полиномам Лежандра.

При α = 1 уравнение сводится к дифференциальному уравнению Чебышева, а полином Гегенбауэра s сводятся к полиномам Чебышева второго рода.

• Они задаются как гипергеометрические ряды Гаусса в некоторых случаях, когда ряд фактически конечен:

$C\; n\; (\; \alpha )\; (z)\; знак\; равно\; (2\; \alpha )\; nn!\; 2\; F\; 1\; (-\; n,\; 2\; \alpha \; +\; n;\; \alpha \; +\; 1\; 2;\; 1\; -\; z\; 2).\; \{\backslash \; displaystyle\; C\_\; \{n\}\; ^\; \{(\backslash \; alpha)\}\; (z)\; =\; \{\backslash \; frac\; \{(2\; \backslash \; alpha)\; \_\; \{n\}\}\; \{n!\}\}\; \backslash ,\; \_\; \{2\}\; F\_\; \{1\}\; \backslash \; left\; (\; -n,\; 2\; \backslash \; alpha\; +\; n;\; \backslash \; alpha\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\};\; \{\backslash \; frac\; \{1-z\}\; \{2\}\}\; \backslash \; right).\}$

(Абрамовиц и Стегун стр.561 ). Здесь (2α) n - возрастающий факториал . Явно

$C\; n\; (\alpha )\; (z)\; =\; \sum \; k\; =\; 0\; \lfloor \; n\; /\; 2\; \rfloor \; (-\; 1)\; k\; \Gamma \; (n\; -\; k\; +\; \alpha )\; \Gamma \; (\alpha )\; k!\; (n\; -\; 2\; k)!\; (2\; з)\; п\; -\; 2\; к.\; \{\backslash \; Displaystyle\; C\_\; \{n\}\; ^\; \{(\backslash \; альфа)\}\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; lfloor\; n\; /\; 2\; \backslash \; rfloor\}\; (-\; 1)\; ^\; \{k\}\; \{\backslash \; frac\; \{\backslash \; Gamma\; (n-k\; +\; \backslash \; alpha)\}\; \{\backslash \; Gamma\; (\backslash \; alpha)\; k!\; (n-2k)!\}\}\; (2z)\; ^\; \{n-2k\}.\}$

• Они являются частными случаями многочленов Якоби (Суетин 2001):

$C\; n\; (\alpha )\; (x)\; =\; (2\; \alpha )\; n\; (\alpha \; +\; 1\; 2)\; n\; P\; n\; (\alpha \; -\; 1/2,\; \alpha \; -\; 1/2)\; (x).\; \{\backslash \; displaystyle\; C\_\; \{n\}\; ^\; \{(\backslash \; alpha)\}\; (x)\; =\; \{\backslash \; frac\; \{(2\; \backslash \; alpha)\; \_\; \{n\}\}\; \{(\backslash \; alpha\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\})\; \_\; \{n\}\}\}\; P\_\; \{n\}\; ^\; \{(\backslash \; alpha\; -1/2,\; \backslash \; alpha\; -1/2)\}\; (x).\}$

в котором $(\theta )\; n\; \{\backslash \; displaystyle\; (\backslash \; theta)\; \_\; \{n\}\}$представляет возрастающий факториал для $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$.

Следовательно, также имеется формула Родригеса

$C\; n\; (\alpha )\; (x)\; =\; (-\; 1)\; n\; 2\; nn!\; \Gamma \; (\alpha \; +\; 1\; 2)\; \Gamma \; (n\; +\; 2\; \alpha )\; \Gamma \; (2\; \alpha )\; \Gamma \; (\alpha \; +\; n\; +\; 1\; 2)\; (1\; -\; x\; 2))\; -\; \alpha \; +\; 1/2\; dndxn\; [(1\; -\; x\; 2)\; n\; +\; \alpha \; -\; 1/2].\; \{\backslash \; Displaystyle\; C\_\; \{n\}\; ^\; \{(\backslash \; alpha)\}\; (x)\; =\; \{\backslash \; frac\; \{(-1)\; ^\; \{n\}\}\; \{2\; ^\; \{n\}\; n!\}\}\; \{\backslash \; frac\; \{\backslash \; Gamma\; (\backslash \; alpha\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\})\; \backslash \; Gamma\; (n\; +\; 2\; \backslash \; alpha)\}\; \{\backslash \; Gamma\; (\; 2\; \backslash \; alpha)\; \backslash \; Gamma\; (\backslash \; alpha\; +\; n\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\})\}\}\; (1-x\; ^\; \{2\})\; ^\; \{-\; \backslash \; alpha\; +1/2\}\; \{\backslash \; frac\; \{d\; ^\; \{n\}\}\; \{dx\; ^\; \{n\}\}\}\; \backslash \; left\; [(1-x\; ^\; \{2\})\; ^\; \{n\; +\; \backslash \; alpha\; -1/2\}\; \backslash \; right].\}$

При фиксированном α полиномы ортогональны на [−1, 1] относительно весовой функции (Abramowitz Stegun p. 774 )

$w\; (z)\; =\; (1\; -\; z\; 2)\; \alpha \; -\; 1\; 2.\; \{\backslash \; displaystyle\; w\; (z)\; =\; \backslash \; left\; (1-z\; ^\; \{2\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}.\}$

То есть, для n ≠ m

$\int \; -\; 1\; 1\; С\; N\; (\alpha )\; (Икс)\; С\; м\; (\alpha )\; (Икс)\; (1\; -\; Икс\; 2)\; \alpha \; -\; 1\; 2\; dx\; =\; 0.\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{-\; 1\}\; ^\; \{1\; \}\; C\_\; \{n\}\; ^\; \{(\backslash \; alpha)\}\; (x)\; C\_\; \{m\}\; ^\; \{(\backslash \; alpha)\}\; (x)\; (1-x\; ^\; \{2\})\; ^\; \{\backslash \; alpha\; -\; \{\backslash \; frac\; \{1\}\; \{\; 2\}\}\}\; \backslash ,\; dx\; =\; 0.\}$

Они нормированы на

$\int \; -\; 1\; 1\; [C\; n\; (\alpha )\; (x)]\; 2\; (1\; -\; x\; 2)\; \alpha \; -\; 1\; 2\; dx\; =\; \pi \; 2\; 1-2\; \alpha \; \Gamma \; (п\; +\; 2\; \alpha )\; п!\; (n\; +\; \alpha )\; [\Gamma \; (\alpha )]\; 2.\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{-\; 1\}\; ^\; \{1\}\; \backslash \; left\; [C\_\; \{n\}\; ^\; \{(\backslash \; alpha)\}\; (x)\; \backslash \; right]\; ^\; \{2\}\; (1-x\; ^\; \{2\})\; ^\; \{\backslash \; альфа\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \backslash ,\; dx\; =\; \{\backslash \; frac\; \{\backslash \; pi\; 2\; ^\; \{1-2\; \backslash \; alpha\}\; \backslash \; Gamma\; (n\; +\; 2\; \backslash \; alpha)\}\; \{n!\; (n\; +\; \backslash \; alpha)\; [\backslash \; Gamma\; (\backslash \; alpha)]\; ^\; \{2\}\}\}.\}$

Полиномы Гегенбауэра естественно появляются как расширения полиномов Лежандра в контексте теории потенциала и гармонический анализ. Ньютоновский потенциал в R имеет расширение, допустимое с α = (n - 2) / 2,

$1\; |\; х\; -\; у\; |\; n\; -\; 2\; =\; \sum \; k\; =\; 0\; \infty \; |\; х\; |\; k\; |\; y\; |\; k\; +\; n\; -\; 2\; C\; k\; (\alpha )\; (x\; \cdot \; y).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{|\; \backslash \; mathbf\; \{x\}\; -\; \backslash \; mathbf\; \{y\}\; |\; ^\; \{n-2\}\}\}\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{|\; \backslash \; mathbf\; \{x\}\; |\; ^\; \{k\}\}\; \{|\; \backslash \; mathbf\; \{y\}\; |\; ^\; \{k\; +\; n-2\}\}\}\; C\_\; \{k\}\; ^\; \{(\backslash \; alpha)\}\; (\backslash \; mathbf\; \{x\}\; \backslash \; cdot\; \backslash \; mathbf\; \{y\}).\}$

Когда n = 3, это дает разложение по полиному Лежандра для гравитационного потенциала. Подобные выражения доступны для расширения ядра Пуассона в шар (Stein Weiss 1971).

Отсюда следует, что величины $C\; k\; ((n\; -\; 2)\; /\; 2)\; (x\; \cdot \; y)\; \{\backslash \; displaystyle\; C\_\; \{k\}\; ^\; \{((n-2)\; /\; 2)\}\; (\; \backslash \; mathbf\; \{x\}\; \backslash \; cdot\; \backslash \; mathbf\; \{y\})\}$- это сферические гармоники, если рассматривать их как функцию только от x . Фактически, это в точности зональные сферические гармоники с точностью до нормирующей постоянной.

Многочлены Гегенбауэра также встречаются в теории положительно определенных функций.

Неравенство Аски – Гаспера читается как

$\sum \; j\; =\; 0\; n\; C\; j\; \alpha \; (x)\; (2\; \alpha \; +\; j\; -\; 1\; j)\; \ge \; 0\; (x\; \ge \; -\; 1,\; \alpha \; \ge \; 1/4).\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{j\; =\; 0\}\; ^\; \{n\}\; \{\backslash \; frac\; \{C\_\; \{j\}\; ^\; \{\backslash \; alpha\}\; (x)\}\; \{2\; \backslash \; alpha\; +\; j-1\; \backslash \; choose\; j\}\}\; \backslash \; geq\; 0\; \backslash \; qquad\; (x\; \backslash \; geq\; -1,\; \backslash ,\; \backslash \; alpha\; \backslash \; geq\; 1/4).\}$

• Многочлены Роджерса, q-аналог многочленов Гегенбауэра
• многочленов Чебышева
• многочленов Романовского

• Абрамовиц, Милтон ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 22». Справочник по математическим функциям с формулами, графиками и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 773. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.*Koornwinder, Tom H.; Wong, Roderick S.C.; Коэкоек, Рулоф; Свартту, Рене Ф. (2010), «Ортогональные многочлены», в Олвер, Фрэнк У. Дж. ; Lozier, Daniel M.; Бойсверт, Рональд Ф.; Кларк, Чарльз У. (ред.), Справочник по математическим функциям NIST, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
• Штейн, Элиас ; Вайс, Гвидо (1971), Введение в анализ Фурье в евклидовых пространствах, Принстон, Нью-Джерси: Princeton University Press, ISBN 978-0-691 -08078-9.
• Суетин П.К. (2001) [1994], Энциклопедия математики, EMS Press.

Конкретные

1. ^Арфкен, Вебер и Харрис (2013) «Математические методы для физиков», 7-е издание; гл. 18,4