В вычислениях, телекоммуникации, теория информации и теория кодирования, код исправления ошибок, иногда код исправления ошибок, (ECC ) используется для контроля ошибок в данных по ненадежным или зашумленным каналам связи. Основная идея заключается в том, что отправитель кодирует сообщение с помощью избыточной информации в форме ECC. Избыточность позволяет получателю обнаруживать ограниченное количество ошибок, которые могут возникать в любом месте сообщения, и часто исправлять эти ошибки без повторной передачи. Американский математик Ричард Хэмминг был пионером в этой области в 1940-х годах и изобрел первый исправляющий ошибки код в 1950 году: код Хэмминга (7,4).
ECC контрастирует с обнаружением ошибок. в том, что обнаруженные ошибки можно исправить, а не просто обнаружить. Преимущество состоит в том, что системе, использующей ECC, не требуется обратный канал для запроса повторной передачи данных при возникновении ошибки. Обратной стороной является то, что к сообщению добавляются фиксированные накладные расходы, что требует более высокой полосы пропускания прямого канала. Таким образом, ECC применяется в ситуациях, когда повторные передачи являются дорогостоящими или невозможными, например, при односторонних каналах связи и при передаче на несколько приемников в многоадресной передаче. Соединения с длительной задержкой также выигрывают; в случае спутника, вращающегося вокруг Урана, повторная передача из-за ошибок может вызвать задержку в пять часов. Информация ECC обычно добавляется к запоминающим устройствам для восстановления поврежденных данных, широко используется в модемах и используется в системах, где основной памятью является память ECC.
Обработка ЕСС в приемнике может применяться к цифровому потоку битов или к демодуляции несущей с цифровой модуляцией. В последнем случае ECC является неотъемлемой частью начального аналого-цифрового преобразования в приемнике. Декодер Витерби реализует алгоритм мягкого решения для демодуляции цифровых данных из аналогового сигнала, искаженного шумом. Многие кодеры / декодеры ECC также могут генерировать сигнал с коэффициентом ошибок по битам (BER), который можно использовать в качестве обратной связи для точной настройки аналоговой приемной электроники.
Максимальная доля ошибок или отсутствующих битов, которые могут быть исправлены, определяется конструкцией кода ECC, поэтому разные коды исправления ошибок подходят для разных условий. Как правило, более сильный код вызывает большую избыточность, которую необходимо передавать с использованием доступной полосы пропускания, что снижает эффективную скорость передачи данных при одновременном улучшении принимаемого эффективного отношения сигнал / шум. Теорема кодирования с шумом канала из Клод Шеннон отвечает на вопрос о том, какая полоса пропускания остается для передачи данных при использовании наиболее эффективного кода, который сводит вероятность ошибки декодирования к нулю. Это устанавливает границы теоретической максимальной скорости передачи информации канала с некоторым заданным базовым уровнем шума. Однако это доказательство неконструктивно и, следовательно, не дает представления о том, как создать код, обеспечивающий производительность. После многих лет исследований некоторые современные системы ECC сегодня очень близки к теоретическому максимуму.
В электросвязи, теории информации и теории кодирования, прямое исправление ошибок (FEC ) или канальное кодирование - это метод, используемый для контроля ошибок в передаче данных по ненадежным или зашумленным каналам связи. Основная идея заключается в том, что отправитель кодирует сообщение с помощью избыточного способа, чаще всего с помощью ECC.
Избыточность позволяет получателю обнаруживать ограниченное количество ошибок, которые могут возникнуть в любом месте сообщения, и часто исправлять эти ошибки без повторной передачи. FEC дает приемнику возможность исправлять ошибки без необходимости использования обратного канала для запроса повторной передачи данных, но за счет фиксированной более высокой полосы пропускания прямого канала. Поэтому FEC применяется в ситуациях, когда повторные передачи являются дорогостоящими или невозможными, например, при односторонних каналах связи и при передаче на несколько приемников в многоадресной передаче. Информация FEC обычно добавляется к запоминающим устройствам (магнитным, оптическим и твердотельным / флэш-накопителям) для восстановления поврежденных данных, широко используется в модемах, используется в системах, где первичной памятью является память ECC, и в ситуациях широковещательной передачи, когда приемник не имеет возможности запрашивать повторную передачу или это может вызвать значительную задержку. Например, в случае спутника, вращающегося вокруг Урана, повторная передача из-за ошибок декодирования может вызвать задержку не менее 5 часов.
Обработка FEC в приемнике может применяться к цифровому битовому потоку или при демодуляции несущей с цифровой модуляцией. Для последнего FEC является неотъемлемой частью начального аналого-цифрового преобразования в приемнике. Декодер Витерби реализует алгоритм мягкого решения для демодуляции цифровых данных из аналогового сигнала, искаженного шумом. Многие кодеры FEC могут также генерировать сигнал с коэффициентом ошибок по битам (BER), который можно использовать в качестве обратной связи для точной настройки аналоговой приемной электроники.
Максимальная доля ошибок или недостающих битов, которые могут быть исправлены, определяется конструкцией ECC, поэтому разные коды прямого исправления ошибок подходят для разных условий. Как правило, более сильный код вызывает большую избыточность, которую необходимо передавать с использованием доступной полосы пропускания, что снижает эффективную скорость передачи данных при одновременном улучшении принимаемого эффективного отношения сигнал / шум. Теорема кодирования канала с шумом Клода Шеннона отвечает на вопрос о том, какая полоса пропускания остается для передачи данных при использовании наиболее эффективного кода, который обращает вероятность ошибки декодирования в ноль. Это устанавливает границы теоретической максимальной скорости передачи информации канала с некоторым заданным базовым уровнем шума. Его доказательство неконструктивно и, следовательно, не дает понимания того, как создать код, обеспечивающий производительность. Однако после многих лет исследований некоторые передовые системы FEC, такие как полярный код, достигают пропускной способности канала Шеннона при гипотезе кадра бесконечной длины.
ECC достигается путем добавления избыточности к передаваемой информации с использованием алгоритма. Избыточный бит может быть сложной функцией многих исходных информационных битов. Исходная информация может появляться или не появляться буквально в закодированном выводе; коды, которые включают немодифицированный ввод в вывод, являются систематическими, тогда как те, которые не включают, являются несистематическими .
Упрощенный пример ECC - передача каждого бита данных 3 раза, что известно как код повторения (3,1) . Через шумный канал приемник может видеть 8 вариантов вывода, см. Таблицу ниже.
| Получен триплет | Интерпретируется как |
|---|---|
| 000 | 0 (без ошибок) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (без ошибок) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
Это позволяет исправить ошибку в любой из трех выборок «большинством голосов» или «демократическим голосованием». Корректирующая способность этого ECC:
Хотя прост в реализации и Это широко используемое тройное модульное резервирование является относительно неэффективным ECC. Более совершенные коды ECC обычно проверяют несколько последних десятков или даже несколько последних сотен ранее принятых битов, чтобы определить, как декодировать текущую небольшую группу битов (обычно в группах от 2 до 8 бит).
Можно сказать, что ECC работает посредством «усреднения шума»; поскольку каждый бит данных влияет на многие передаваемые символы, искажение одних символов шумом обычно позволяет извлекать исходные пользовательские данные из других неповрежденных принятых символов, которые также зависят от тех же пользовательских данных.
Большинство телекоммуникационных систем используют фиксированный канальный код, рассчитанный на ожидаемый наихудший случай частоты ошибок по битам, а затем вообще не работают если частота ошибок по битам станет еще хуже. Однако некоторые системы адаптируются к данным условиям ошибки канала: некоторые экземпляры гибридного автоматического запроса на повторение используют фиксированный метод ECC, пока ECC может обрабатывать частоту ошибок, затем переключаются на ARQ когда частота ошибок становится слишком высокой; адаптивная модуляция и кодирование использует различные скорости ECC, добавляя больше битов исправления ошибок на пакет, когда в канале более высокие частоты ошибок, или удаляя их, когда они не нужны.
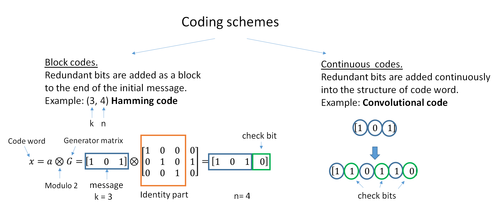 Краткая классификация кодов коррекции ошибок.
Краткая классификация кодов коррекции ошибок. Двумя основными категориями кодов ECC являются блочные коды и сверточные коды.
Существует много типов блочных кодов; Кодирование Рида-Соломона примечательно тем, что оно широко используется в компакт-дисках, DVD и жестких дисках. Другие примеры классических блочных кодов включают Голея, BCH, многомерную четность и коды Хэмминга.
ECC Хэмминга обычно используются для исправления NAND flash ошибки памяти. Это обеспечивает исправление однобитовых ошибок и обнаружение двухбитовых ошибок. Коды Хэмминга подходят только для более надежной одноуровневой ячейки (SLC) NAND. Более плотная многоуровневая ячейка (MLC) NAND может использовать многобитовый корректирующий ECC, такой как BCH или Reed-Solomon. NOR Flash обычно не использует никакого исправления ошибок.
Классические блочные коды обычно декодируются с использованием алгоритмов жесткого решения, что означает, что для каждого входного и выходного сигнала принимается жесткое решение, будет ли он соответствует единице или нулю бит. Напротив, сверточные коды обычно декодируются с использованием алгоритмов мягкого решения, таких как алгоритмы Витерби, MAP или BCJR, которые обрабатывают (дискретизированные) аналоговые сигналы и которые допускают гораздо более высокие ошибки - производительность коррекции, чем декодирование с жестким решением.
Почти все классические блочные коды применяют алгебраические свойства конечных полей. Поэтому классические блочные коды часто называют алгебраическими кодами.
В отличие от классических блочных кодов, которые часто определяют способность обнаружения или исправления ошибок, многие современные блочные коды, такие как коды LDPC, не имеют таких гарантий. Вместо этого современные коды оцениваются с точки зрения их частоты ошибок по битам.
Большинство кодов прямого исправления ошибок исправляют только перевороты битов, но не вставки или удаления битов. В этой настройке расстояние Хэмминга является подходящим способом измерения коэффициента битовых ошибок. Несколько кодов прямого исправления ошибок предназначены для исправления вставки и удаления битов, например, коды маркеров и коды водяных знаков. Расстояние Левенштейна является более подходящим способом измерения частоты ошибок по битам при использовании таких кодов.
Фундаментальный принцип ECC состоит в добавлении избыточных битов, чтобы помочь декодеру узнать истинное сообщение, которое было закодировано передатчик. Кодовая скорость данной системы ЕСС определяется как соотношение между количеством информационных битов и общим количеством битов (то есть информацией плюс биты избыточности) в данном коммуникационном пакете. Кодовая скорость, следовательно, является действительным числом. Низкая кодовая скорость, близкая к нулю, подразумевает сильный код, который использует много избыточных битов для достижения хорошей производительности, в то время как большая кодовая скорость, близкая к 1, подразумевает слабый код.
Избыточные биты, защищающие информацию, должны передаваться с использованием тех же коммуникационных ресурсов, которые они пытаются защитить. Это вызывает фундаментальный компромисс между надежностью и скоростью передачи данных. В одном крайнем случае сильный код (с низкой кодовой скоростью) может вызвать значительное увеличение SNR приемника (отношение сигнал / шум), уменьшая частоту ошибок по битам, за счет снижения эффективной скорости передачи данных. С другой стороны, без использования какого-либо ECC (то есть кодовой скорости, равной 1) используется полный канал для целей передачи информации за счет того, что биты остаются без какой-либо дополнительной защиты.
Один интересный вопрос заключается в следующем: насколько эффективным с точки зрения передачи информации может быть ECC, имеющий незначительную частоту ошибок декодирования? На этот вопрос ответил Клод Шеннон с его второй теоремой, которая гласит, что пропускная способность канала - это максимальная скорость передачи данных, достижимая для любого ECC, частота ошибок которого стремится к нулю: его доказательство основано на гауссовском случайном кодировании, которое не подходит для реального мира. Приложения. Верхняя граница, заданная работой Шеннона, вдохновила на долгий путь к разработке ECC, которые могут приблизиться к пределу конечных характеристик. Различные коды сегодня могут достигать почти предела Шеннона. Однако ECC, обеспечивающие пропускную способность, обычно чрезвычайно сложно реализовать.
Наиболее популярные ECC имеют компромисс между производительностью и вычислительной сложностью. Обычно их параметры дают диапазон возможных кодовых скоростей, которые можно оптимизировать в зависимости от сценария. Обычно эта оптимизация выполняется для достижения низкой вероятности ошибки декодирования при минимальном влиянии на скорость передачи данных. Другим критерием оптимизации кодовой скорости является уравновешивание низкой частоты ошибок и количества повторных передач с учетом энергетических затрат на связь.
Классические (алгебраические) блочные коды а сверточные коды часто комбинируются в схемах конкатенированного кодирования, в которых сверточный код, декодированный по Витерби с короткой ограниченной длиной, выполняет большую часть работы, а блочный код (обычно Рида-Соломона) с большим размером символа и длиной блока «стирает» любые ошибки, сделанные сверточным декодером. Однопроходное декодирование с использованием этого семейства кодов с исправлением ошибок может дать очень низкий уровень ошибок, но для условий передачи на большие расстояния (например, в глубоком космосе) рекомендуется итеративное декодирование.
Составные коды были стандартной практикой в спутниковой связи и связи в дальнем космосе с тех пор, как "Вояджер-2 " впервые применил эту технику во время встречи с Ураном в 1986 году. Аппарат Galileo использовал итеративные конкатенированные коды для компенсации условий очень высокой частоты ошибок, вызванных отказом антенны.
Коды с проверкой на четность с низкой плотностью (LDPC) - это класс высокоэффективных линейных блочных кодов, созданных из множества кодов одиночной проверки на четность (SPC). Они могут обеспечить производительность, очень близкую к пропускной способности канала (теоретический максимум), используя подход итеративного декодирования с мягким решением, при линейной временной сложности с точки зрения длины их блока. Практические реализации в значительной степени полагаются на параллельное декодирование составляющих кодов SPC.
Коды LDPC были впервые введены Робертом Г. Галлагером в его докторской диссертации в 1960 году, но из-за вычислительных усилий при реализации кодера и декодера и введения Рида-Соломона коды, они в основном игнорировались до 1990-х годов.
Коды LDPC теперь используются во многих недавних стандартах высокоскоростной связи, таких как DVB-S2 (цифровое видеовещание - спутниковое - второе поколение), WiMAX ( стандарт IEEE 802.16e для микроволновой связи), высокоскоростная беспроводная локальная сеть (IEEE 802.11n ), 10GBase-T Ethernet (802.3an) и G.hn/G.9960 (Стандарт ITU-T для организации сетей по линиям электропередач, телефонным линиям и коаксиальному кабелю). Другие коды LDPC стандартизированы для стандартов беспроводной связи в пределах 3GPP MBMS (см. исходные коды ).
Турбокодирование - это схема повторяющегося мягкого декодирования, которая объединяет два или более относительно простых сверточных кода и перемежитель для создания блочного кода, который может работать с точностью до долей децибела. предела Шеннона. Предшествующие LDPC-коды с точки зрения практического применения, теперь они обеспечивают аналогичную производительность.
Одним из первых коммерческих приложений турбо-кодирования была технология цифровой сотовой связи CDMA2000 1x (TIA IS-2000), разработанная Qualcomm и продаваемая Verizon Беспроводная связь, Sprint и другие операторы связи. Он также используется для развития CDMA2000 1x специально для доступа в Интернет, 1xEV-DO (TIA IS-856). Как и 1x, EV-DO был разработан Qualcomm и продается Verizon Wireless, Sprint и другими операторами (маркетинговое название Verizon для 1xEV-DO - Широкополосный доступ, потребительские и бизнес-маркетинговые названия компании Sprint для 1xEV-DO - Power Vision и Mobile Broadband соответственно).
Иногда необходимо декодировать только отдельные биты сообщения или проверить, является ли данный сигнал кодовым словом, и делать это, не глядя на все сигнал. Это может иметь смысл в настройке потоковой передачи, где кодовые слова слишком велики для того, чтобы их можно было классически декодировать достаточно быстро, и где на данный момент интересны только несколько битов сообщения. Также такие коды стали важным инструментом в теории сложности вычислений, например, для разработки вероятностно проверяемых доказательств.
Локально декодируемые коды являются кодами с исправлением ошибок, для которых отдельные биты сообщение может быть восстановлено вероятностно, если посмотреть только на небольшое (скажем, постоянное) количество позиций кодового слова, даже после того, как кодовое слово было искажено на некоторой постоянной доле позиций. Локально тестируемые коды - это коды с исправлением ошибок, для которых можно вероятностно проверить, близок ли сигнал к кодовому слову, посмотрев только на небольшое количество позиций сигнала.
 Краткая иллюстрация идеи чередования.
Краткая иллюстрация идеи чередования. Чередование часто используется в системах цифровой связи и хранения для повышения производительности кодов прямого исправления ошибок. Многие каналы связи не лишены памяти: ошибки обычно возникают в пакетах, а не независимо друг от друга. Если количество ошибок в кодовом слове превышает возможности кода исправления ошибок, ему не удается восстановить исходное кодовое слово. Чередование облегчает эту проблему путем перетасовки исходных символов по нескольким кодовым словам, тем самым создавая более равномерное распределение ошибок. Поэтому перемежение широко используется для пакетной коррекции ошибок.
. Анализ современных повторяющихся кодов, таких как турбокоды и коды LDPC, обычно предполагает независимое распределение ошибок.. Поэтому системы, использующие коды LDPC, обычно используют дополнительное перемежение символов в кодовом слове.
Для турбокодов перемежитель является неотъемлемым компонентом, и его правильная конструкция имеет решающее значение для хорошей производительности. Алгоритм итеративного декодирования работает лучше всего, когда нет коротких циклов в графе коэффициентов, который представляет декодер; перемежитель выбран, чтобы избежать коротких циклов.
Конструкции перемежителя включают:
В системах связи с несколькими несущими может использоваться перемежение по несущим для обеспечения частотного разнесения., например, для уменьшения частотно-избирательного замирания или узкополосных помех.
Передача без перемежения :
Сообщение без ошибок: aaaabbbbccccddddeeeeffffgggg Передача с пакетной ошибкой: aaaabbbbccc____deeeeffffgggg
Здесь каждая группа одинаковых букв представляет 4-битное однобитовое кодовое слово с исправлением ошибок. Кодовое слово cccc изменяется в один бит и может быть исправлено, но кодовое слово dddd изменяется в трех битах, поэтому либо оно не может быть декодировано вообще, либо может быть декодировано неправильно.
С чередованием :
Ошибка- свободные кодовые слова: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Передача с ошибкой пакета: abcdefgabcd____bcdefgabcdefg Полученные кодовые слова после деинтерлейвинга: "aa_abbb_gg2ccd_dd>,", ",", ",", ","Передача без чередования :
Исходное переданное предложение: ThisIsAnExampleOfInterleaving Полученное предложение с пакетной ошибкой: ThisIs______pleOfInterleavingТермин «AnExample» оказывается в основном неразборчивым и трудным для исправления.
С чередованием :
Переданное предложение: ThisIsAnExampleOfInterleaving... Безошибочная передача: TIEpfeaghsxlIrv.iAaenli.snmOten. Получено предложение с пакетной ошибкой: TIEpfe ______ Irv.iAaenli.snmOten. Полученное предложение после деинтерлейвинга: T_isI_AnE_amp_eOfInterle_vin _...Ни одно слово не потеряно полностью, а недостающие буквы можно восстановить с минимальными догадками.
Недостатки чередования
Использование методов чередования увеличивает общую задержку. Это связано с тем, что весь чередующийся блок должен быть принят до того, как пакеты могут быть декодированы. Также перемежители скрывают структуру ошибок; Без перемежителя более совершенные алгоритмы декодирования могут использовать структуру ошибок и обеспечивать более надежную связь, чем более простой декодер, объединенный с перемежителем. Пример такого алгоритма основан на структурах нейронной сети .
Программное обеспечение для кодов с исправлением ошибокМоделирование поведения кодов с исправлением ошибок (ECC) в программном обеспечении является обычной практикой для разработки, проверки и улучшения кодов ECC. Предстоящий стандарт беспроводной связи 5G поднимает новый диапазон приложений для программных ECC: Облачные сети радиодоступа (C-RAN) в контексте Программно-определяемого радио (SDR). Идея состоит в том, чтобы напрямую использовать программные ECC в коммуникациях. Например, в 5G программные ECC могут быть расположены в облаке, а антенны могут быть подключены к этим вычислительным ресурсам: таким образом повышается гибкость сети связи и, в конечном итоге, повышается энергоэффективность системы.
В этом контексте существует различное доступное программное обеспечение с открытым исходным кодом, перечисленное ниже (не является исчерпывающим).
- AFF3CT (Панель инструментов быстрого исправления ошибок): полная цепочка связи на C ++ (многие поддерживаемые коды, такие как Turbo, LDPC, полярные коды и т. Д.), Очень быстрая и специализированная на канальном кодировании (может использоваться как программа для моделирования или как библиотека для SDR).
- IT ++ : библиотека классов и функций C ++ для линейной алгебры, числовой оптимизации, обработки сигналов, связи и статистики.
- OpenAir : реализация (на языке C) спецификаций 3GPP, касающихся Evolved Packet Core Networks.
Список кодов исправления ошибок
Расстояние Код 2 (обнаружение единичной ошибки) Четность 3 (исправление одиночной ошибки) Тройное модульное резервирование 3 (исправление одиночной ошибки) совершенное Хэмминга, такое как Хэмминга (7,4) 4 (SECDED ) Расширенный Хэмминга 5 (исправление двойной ошибки) 6 (исправление двойной ошибки / обнаружение тройной ошибки) 7 (исправление трех ошибок) совершенный двоичный код Голея 8 (TECFED) расширенный двоичный код Голея
- коды AN
- код BCH, который может быть разработан для исправления любого произвольного количества ошибок в кодовом блоке.
- код Бергера
- код постоянного веса
- сверточный код
- Расширительные коды
- Групповые коды
- коды Голея, из которых двоичный код Голея представляет практический интерес
- код Гоппа, используемый в Криптосистема Мак-Элиса
- Код Адамара
- Код Хагельбаргера
- Код Хэмминга
- Код на основе латинского квадрата для небелого шума (преобладающий, например, в широкополосной связи по сравнению с линиями электропередач)
- Лексикографический код
- Линейное сетевое кодирование, тип кода с исправлением стирания в сетях вместо двухточечных ссылок
- Длинный код
- Код проверки четности с низкой плотностью, также известный как код Галлагера, как архетип для кодов разреженного графа
- LT-кода, который является почти оптимальным бесскоростным кодом коррекции стирания (код Фонтана)
- m из n кодов
- Онлайн-код, почти оптимальный код бесскоростной коррекции стирания
- Полярный код (codi ng теория)
- Код Raptor, почти оптимальный код с бесскоростной коррекцией стирания
- Исправление ошибок Рида – Соломона
- Код Рида – Маллера
- Код повторения-накопления
- Коды повторения, например, Тройная модульная избыточность
- Спинальный код, бесскоростной нелинейный код, основанный на псевдослучайных хэш-функциях
- Код Торнадо, почти оптимальный код коррекции стирания, и предшественник кодов Фонтана
- Турбо-код
- код Уолша – Адамара
- Циклические проверки избыточности (CRC) могут исправлять 1-битные ошибки для сообщений не более
бит длиной для оптимальных порождающих полиномов степени
, см. Математика циклических проверок избыточности # Битовые фильтры
См. Также
- Скорость кода
- Коды стирания
- Декодер с мягким решением
- Пакетный код исправления ошибок
- Обнаружение и исправление ошибок
- Ошибка -корректирующие коды с обратной связью
СсылкиДополнительная литература
- Clark, Jr., George C.; Каин, Дж. Бибб (1981). Кодирование с коррекцией ошибок для цифровой связи. Нью-Йорк, США: Plenum Press. ISBN 0-306-40615-2. ISBN 978-0-306-40615-7.
- Уикер, Стивен Б. (1995). Системы контроля ошибок для цифровой связи и хранения. Энглвуд Клиффс, Нью-Джерси, США: Прентис-Холл. ISBN 0-13-200809-2. ISBN 978-0-13-200809-9.
- Уилсон, Стивен Г. (1996). Цифровая модуляция и кодирование. Энглвуд Клиффс, Нью-Джерси, США: Прентис-Холл. ISBN 0-13-210071-1. ISBN 978-0-13-210071-7.
- "Код коррекции ошибок в одноуровневой ячейке NAND флэш-памяти « 16 февраля 2007 г.
- « Код исправления ошибок во флэш-памяти NAND » 29 ноября 2004 г.
- Наблюдения за ошибками, исправлениями и доверием зависимых систем, Джеймс Гамильтон, 26 февраля 2012 г.
- Сферические упаковки, решетки и группы, Дж. Х. Конвей, NJA Sloane, Springer Science Business Media, 9 марта 2013 г. - Математика - 682 страницы.
Внешние ссылки
- Морелос -Зарагоса, Роберт (2004). "Страница корректирующих кодов (ECC)". Проверено 5 марта 2006 г.
- lpdec: библиотека для декодирования LP и связанных вещей (Python)