Войти
3-битный двоичный куб для поиска расстояния Хэмминга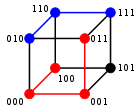 
Два примера расстояний: 100 → 011 имеет расстояние 3; 010 → 111 имеет расстояние 2 Минимальное расстояние между любыми двумя вершинами - это расстояние Хэмминга между двумя двоичными строками. 
4-битный двоичный код tesseract для нахождения расстояния Хэмминга.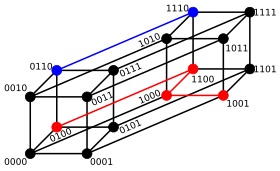 
Два примера дистанции: 0100 → 1001 имеет расстояние 3; 0110 → 1110 имеет расстояние 1 В теории информации, расстояние Хэмминга между двумя строками одинаковой длины - это количество позиций, на которых соответствующие символы разные. Другими словами, он измеряет минимальное количество замен, необходимых для преобразования одной строки в другую, или минимальное количество ошибок, которые могли бы преобразовать одну строку в другую. В более общем контексте расстояние Хэмминга - это одна из нескольких строковых метрик для измерения расстояния редактирования между двумя последовательностями. Он назван в честь американского математика Ричарда Хэмминга.
Основное применение - теория кодирования, а точнее блочные коды, в которых строки равной длины векторов над конечным полем.
Расстояние Хэмминга между двумя строками символов одинаковой длины - это количество позиций, в которых соответствующие символы различны.
Среди других возможностей символы могут быть буквами, битами или десятичными цифрами. Например, расстояние Хэмминга между:
Для фиксированной длины n расстояние Хэмминга является метрикой на множестве слов длины n. (также известное как пространство Хэмминга ), поскольку оно удовлетворяет условиям неотрицательности, симметрии, расстояние Хэмминга двух слов равно 0 тогда и только тогда, когда два слова идентичны, и оно удовлетворяет условию неравенство треугольника : Действительно, если мы зафиксируем три слова a, b и c, то всякий раз, когда есть разница между i-й буквой a и i-й буквой c, тогда должна быть разница между i-й буквой a и i-й буквой b или между i-й буквой b и i-й буквой c. Следовательно, расстояние Хэмминга между a и c не больше суммы расстояния Хэмминга ces между a и b и между b и c. Расстояние Хэмминга между двумя словами a и b также можно рассматривать как вес Хэмминга для a - b при соответствующем выборе оператора -, так же, как разница между двумя целыми числами можно рассматривать как расстояние от ноль на числовой строке.
Для двоичных строк a и b расстояние Хэмминга равно количеству единиц (совокупность ) в a XOR b. Метрическое пространство двоичных строк длины n с расстоянием Хэмминга известно как куб Хэмминга; как метрическое пространство оно эквивалентно набору расстояний между вершинами в графе гиперкуба. Можно также рассматривать двоичную строку длины n как вектор в 
Минимальное расстояние Хэмминга используется для определения некоторых важных понятий в теории кодирования, таких как ошибка коды обнаружения и исправления ошибок. В частности, код C называется обнаруживающим k ошибок тогда и только тогда, когда минимальное расстояние Хэмминга между любыми двумя его кодовыми словами составляет не менее k + 1.
Например рассмотрим код, состоящий из двух кодовых слов «000» и «111». Расстояние Хэмминга между этими двумя словами равно 3, и, следовательно, это k = 2 обнаружения ошибок. Это означает, что если один или два бита перевернуты, ошибка может быть обнаружена. Если три бита перевернуты, то «000» становится «111», и ошибка не может быть обнаружена.
Код C называется исправляющим k ошибок, если для каждого слова w в базовом пространстве Хэмминга H существует не более одного кодового слова c (из C) такое, что расстояние Хэмминга между w и c не больше k. Другими словами, код исправляет k-ошибки тогда и только тогда, когда минимальное расстояние Хэмминга между любыми двумя его кодовыми словами составляет не менее 2k + 1. С геометрической точки зрения это легче понять, поскольку любые замкнутые шары радиуса k с центрами на различных кодовых словах не пересекаются. Эти шары также называются сферами Хэмминга в этом контексте.
Например, рассмотрим тот же 3-битный код, состоящий из двух кодовых слов «000» и «111». Пространство Хэмминга состоит из 8 слов 000, 001, 010, 011, 100, 101, 110 и 111. Кодовое слово «000» и слова однобитовой ошибки «001», «010», «100» меньше или равно расстоянию Хэмминга от 1 до «000». Точно так же кодовое слово «111» и его слова с однократной ошибкой бита «110», «101» и «011» находятся в пределах 1 расстояния Хэмминга от исходного «111». В этом коде ошибка на один бит всегда находится в пределах 1 расстояния Хэмминга от исходных кодов, и код может быть исправляющим на 1 ошибку, то есть k = 1. Минимальное расстояние Хэмминга между «000» и «111» равно 3, что удовлетворяет 2k + 1 = 3.
Таким образом, код с минимальным расстоянием Хэмминга d между своими кодовыми словами может обнаруживать не более d-1 ошибок и может исправить ошибки ⌊ (d-1) / 2⌋. Последнее число также называется радиусом упаковки или способностью кода исправлять ошибки.
Расстояние Хэмминга названо в честь Ричарда Хэмминга, который представил эту концепцию в своей фундаментальной статье о кодах Хэмминга, кодах обнаружения и исправления ошибок, в 1950 году. Весовой анализ битов Хэмминга используется в нескольких дисциплинах, включая теорию информации, теория кодирования и криптография.
Используется в электросвязи для подсчета количества перевернутых битов в двоичном слове фиксированной длины в качестве оценки ошибки, поэтому иногда его называют сигнальным расстоянием . Для q-ичных строк в алфавите размера q ≥ 2 расстояние Хэмминга применяется в случае q-арного симметричного канала, а расстояние Ли используется для фазовой манипуляции или, в более общем смысле, каналов, восприимчивых к воздействию, поскольку расстояние Ли учитывает ошибки в ± 1. Если 
Расстояние Хэмминга также используется в систематике как мера генетического расстояние.
Однако для сравнения строк разной длины или строк, где следует ожидать не только подстановок, но и вставок или удалений, более подходящей метрикой является расстояние Левенштейна..
В межкомпонентных соединениях процессоров динамическое потребление энергии зависит от количества переходов. В схеме сигнализации уровня количество переходов зависит от расстояния Хэмминга между последовательно передаваемыми шинами. Следовательно, уменьшая это расстояние Хэмминга, можно уменьшить энергию перемещения данных.
Следующая функция, написанная на Python 3.7, возвращает расстояние Хэмминга между двумя строками:
def hamming_distance (string1, string2): dist_counter = 0 for n in range ( len (строка1)): если строка1 [n]! = строка2 [n]: dist_counter + = 1 return dist_counter
Или, в более коротком выражении:
sum (xi! = yi для xi, yi в zip ( x, y))
Функция hamming_distance (), реализованная в Python 2.3+, вычисляет расстояние Хэмминга между двумя строками (или другими итеративными объектами) равной длины путем создания последовательности логических значений, указывающих несоответствия и совпадения между соответствующими позициями на двух входах, а затем суммирования последовательности со значениями False и True, интерпретируемыми как ноль и один.
def hamming_distance (s1, s2) ->int: "" "Возвращает расстояние Хэмминга между последовательностями одинаковой длины." "" If len (s1)! = Len (s2): raise ValueError ("Не определено для последовательностей неравная длина. ") return sum (el1! = el2 for el1, el2 in zip (s1, s2))где функция zip () объединяет две коллекции одинаковой длины попарно.
Следующая функция C вычислит расстояние Хэмминга двух целых чисел (рассматриваемых как двоичные значения, то есть как последовательности битов). Время выполнения этой процедуры пропорционально расстоянию Хэмминга, а не количеству битов на входах. Он вычисляет побитово исключающее или из двух входных данных, а затем находит вес Хэмминга результата (количество ненулевых битов), используя алгоритм Wegner (1960), который многократно находит и очищает ненулевой бит младшего порядка. Некоторые компиляторы поддерживают функцию __builtin_popcount, которая может вычислить это, используя специализированное аппаратное обеспечение процессора, если оно доступно.
int hamming_distance (без знака x, без знака y) {int dist = 0; // Подсчитываем количество битов, установленных для (unsigned val = x ^ y; val>0; val = val>>1) {// Если установлен бит A, увеличиваем счетчик if (val 1) dist ++; // Очистить (удалить) бит младшего разряда val} // Вернуть количество различающихся битов return dist; }Более быстрая альтернатива - использовать инструкцию ассемблера подсчета населения (popcount). Некоторые компиляторы, такие как GCC и Clang, делают его доступным через встроенную функцию:
// Расстояние Хэмминга для 32-битных целых чисел int hamming_distance32 (unsigned int x, unsigned int y) {return __builtin_popcount (x ^ y); } // Расстояние Хэмминга для 64-битных целых чисел int hamming_distance64 (unsigned long long x, unsigned long long y) {return __builtin_popcountll (x ^ y); }
Математический портал 
Эта статья включает общедоступные материалы из документ Управления общих служб : «Федеральный стандарт 1037C».