 Шаг SubBytes, один из четырех этапов в раунде AES Шаг SubBytes, один из четырех этапов в раунде AES | |
| Генерал | |
|---|---|
| Дизайнеры | Винсент Риджмен, Джоан Дэмен |
| Впервые опубликовано | 1998 |
| На основе | Square |
| Преемники | Анубис, Гран Крю, Калина |
| Сертификация | Победитель AES, CRYPTREC, NESSIE, NSA |
| Детали шифра | |
| Размеры ключей | 128, 192 или 256 бит |
| Размеры блоков | 128 бит |
| Структура | Сеть замещения – перестановки |
| Раунды | 10, 12 или 14 (в зависимости от размера ключа) |
| Лучший публичный криптоанализ | |
| Были опубликованы атаки, которые в вычислительном отношении быстрее, чем полный перебор атака, хотя по состоянию на 2013 год ни одна из них не является вычислительно выполнимой. Для AES-128 ключ может быть восстановлен с вычислительной сложностью 2, используя атаку biclique . Для бикликовых атак на AES-192 и AES-256 применяются вычислительные сложности 2 и 2 соответственно. Атаки с использованием связанных ключей могут взломать AES-192 и AES-256 со сложностями 2 и 2 как по времени, так и по данным, соответственно. | |
Расширенный стандарт шифрования (AES ), также известный под своим первоначальным названием Rijndael (голландское произношение: ), является спецификацией для шифрования электронных данных, установленных Национальным институтом стандартов и технологий (NIST) США в 2001 году.
AES является подмножеством блочного шифра Rijndael , разработанного двумя бельгийские криптографы, Винсент Риджмен и Джоан Дэмен, которые представили предложение в NIST во время процесса выбора AES. Rijndael - это семейство шифров с разными размерами ключей и блоков. Для AES NIST выбрал трех членов семейства Rijndael, каждый с размером блока 128 бит, но с тремя разными длинами ключей: 128, 192 и 256 бит.
AES был принят США. правительство и сейчас используется во всем мире. Он заменяет Стандарт шифрования данных (DES), который был опубликован в 1977 году. Алгоритм, описанный AES, представляет собой алгоритм с симметричным ключом, что означает, что один и тот же ключ используется как для шифрования, так и расшифровка данных.
В Соединенных Штатах Америки AES был объявлен NIST как US FIPS PUB 197 (FIPS 197) 26 ноября 2001 г. Это объявление последовало за пятилетним процессом стандартизации, в ходе которого пятнадцать были представлены и оценены конкурирующие конструкции, прежде чем шифр Rijndael был выбран как наиболее подходящий (подробнее см. процесс Advanced Encryption Standard ).
AES включен в стандарт ISO /IEC 18033-3. AES вступил в силу в качестве стандарта федерального правительства США 26 мая 2002 г. после утверждения министром торговли США. AES доступен во многих различных пакетах шифрования и является первым (и единственным) общедоступным шифром, одобренным Агентством национальной безопасности США (NSA) для совершенно секретно информацию при использовании в криптографическом модуле, одобренном NSA (см. Безопасность AES ниже).
Определен расширенный стандарт шифрования (AES) в каждом из:
AES основан на принцип конструкции, известный как сеть замещения-перестановки, эффективен как в программном, так и в аппаратном отношении. В отличие от своего предшественника DES, AES не использует сеть Фейстеля. AES - это вариант Rijndael с фиксированным размером блока , равным 128 бит, и размером ключа , равным 128, 192 или 256 бит. Напротив, Rijndael как таковой определяется с размерами блоков и ключей, которые могут быть любым кратным 32 битам, минимум 128 и максимум 256 бит.
AES работает с массивом байтов 4 × 4 порядка старшего столбца, называемого состоянием. Большинство вычислений AES выполняется в конкретном конечном поле.
, например, 16 байтах, 

Размер ключа, используемый для шифра AES, определяет количество раундов преобразования, которые преобразуют ввод, называемый незашифрованным текстом, в окончательный вывод, называется зашифрованным текстом. Количество раундов следующее:
Каждый раунд состоит из нескольких этапов обработки, включая один, который зависит от самого ключа шифрования. Набор обратных циклов применяется для преобразования зашифрованного текста обратно в исходный открытый текст с использованием того же ключа шифрования.
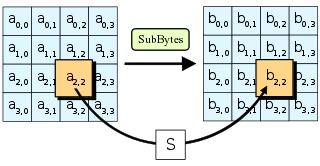 На шаге SubBytes каждый байт в состоянии заменяется его записью в фиксированной 8-битной таблице поиска S; b ij = S (a ij).
На шаге SubBytes каждый байт в состоянии заменяется его записью в фиксированной 8-битной таблице поиска S; b ij = S (a ij).На этапе SubBytes каждый байт 



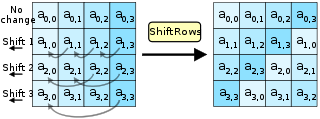 На шаге ShiftRows байты в каждой строке состояния циклически сдвигаются влево. Число мест, на которые смещается каждый байт, различается постепенно для каждой строки.
На шаге ShiftRows байты в каждой строке состояния циклически сдвигаются влево. Число мест, на которые смещается каждый байт, различается постепенно для каждой строки. Шаг ShiftRows работает со строками состояния; он циклически сдвигает байты в каждой строке на определенное смещение. Для AES первая строка оставлена без изменений. Каждый байт второй строки сдвигается на единицу влево. Аналогичным образом третья и четвертая строки сдвигаются на два и три смещения соответственно. Таким образом, каждый столбец выходного состояния шага ShiftRows состоит из байтов из каждого столбца входного состояния. Важность этого шага состоит в том, чтобы избежать независимого шифрования столбцов, в этом случае AES выродится в четыре независимых блочных шифра.
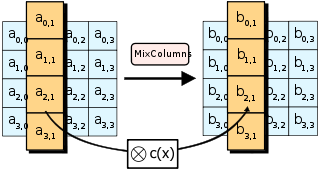 На шаге MixColumns каждый столбец состояния умножается на фиксированный многочлен
На шаге MixColumns каждый столбец состояния умножается на фиксированный многочлен  .
.На этапе MixColumns четыре байта каждого столбца состояния объединяются с использованием обратимого линейного преобразования. Функция MixColumns принимает четыре байта в качестве входных и выводит четыре байта, причем каждый входной байт влияет на все четыре выходных байта. Вместе с ShiftRows, MixColumns обеспечивает распространение в шифре.
Во время этой операции каждый столбец преобразуется с использованием фиксированной матрицы (матрица, умноженная слева на столбец, дает новое значение столбца в состоянии):

Матричное умножение состоит из умножения и сложения записей. Записи обрабатываются байтами как коэффициенты полинома порядка 


В более общем смысле каждый столбец рассматривается как многочлен над 


![{\ displaystyle \ operatorname {GF} (2) [ x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6334bd0b6ddc3a60f9d7590f71c74e11f780b80f)

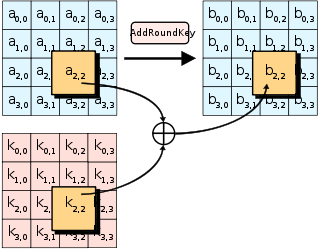 На шаге AddRoundKey каждый байт состояния комбинируется с байтом подключа раунда с помощью операция XOR (⊕).
На шаге AddRoundKey каждый байт состояния комбинируется с байтом подключа раунда с помощью операция XOR (⊕). На этапе AddRoundKey подключ объединяется с состоянием. Для каждого раунда подключ получается из основного ключа с использованием расписания ключей Rijndael ; каждый подключ имеет тот же размер, что и состояние. Подключ добавляется путем объединения каждого байта состояния с соответствующим байтом подключа с помощью побитовой XOR.
В системах с 32-битными или большими словами это возможно для ускорения выполнения этого шифра путем объединения шагов SubBytes и ShiftRows с шагом MixColumns путем преобразования их в последовательность поиска по таблице. Для этого требуются четыре 32-битные таблицы с 256 записями (вместе занимающие 4096 байт). Затем цикл может быть выполнен с помощью 16 операций поиска в таблице и 12 32-битных операций исключающего ИЛИ, за которыми следуют четыре 32-битных операции исключающего ИЛИ на этапе AddRoundKey. В качестве альтернативы, операция поиска в таблице может выполняться с одной 32-битной таблицей с 256 записями (занимающей 1024 байта) с последующими операциями кругового вращения.
Используя байтовый подход, можно объединить шаги SubBytes, ShiftRows и MixColumns в одну операцию раунда.
Агентство национальной безопасности (АНБ) проверило всех финалистов AES, включая Риджндала, и заявило, что все они достаточно защищены для несекретных данных правительства США. В июне 2003 года правительство США объявило, что AES может использоваться для защиты секретной информации :
. Дизайн и надежность всех длин ключей алгоритма AES (т. Е. 128, 192 и 256) достаточны для защиты секретной информации. до СЕКРЕТНОГО уровня. СОВЕРШЕННО СЕКРЕТНАЯ информация потребует использования ключей длиной 192 или 256. Реализация AES в продуктах, предназначенных для защиты систем национальной безопасности и / или информации, должна быть проверена и сертифицирована NSA до их приобретения и использования.
AES имеет 10 циклов для 128-битных ключей, 12 циклов для 192-битных ключей и 14 раундов для 256-битных ключей.
К 2006 году самые известные атаки были на 7 раундов для 128-битных ключей, 8 раундов для 192-битных ключей и 9 раундов для 256-битных ключей.
Для криптографов криптографический «взлом» - это что-то более быстрое, чем атака полным перебором, то есть выполнение одного пробного дешифрования для каждого возможного ключа в последовательности (см. Криптоанализ ). Таким образом, перерыв может включать результаты, которые недостижимы с использованием современных технологий. Несмотря на то, что теоретические исследования непрактичны, иногда они могут дать представление о моделях уязвимости. Самая крупная успешная публично известная атака грубой силы на широко применяемый алгоритм шифрования блочного шифрования была проведена с использованием 64-битного ключа RC5, разработанного distribution.net в 2006 году.
Пространство ключей увеличивается в 2 раза на каждый дополнительный бит длины ключа, и если каждое возможное значение ключа равновероятно, это приводит к удвоению среднего времени поиска ключа методом перебора. Это означает, что усилие перебора увеличивается экспоненциально с увеличением длины ключа. Длина ключа сама по себе не означает защиты от атак, поскольку существуют шифры с очень длинными ключами, которые оказались уязвимыми.
AES имеет довольно простую алгебраическую основу. В 2002 г. Николас Куртуа и Йозеф Пипжик объявили о теоретической атаке, названной «XSL-атака », с целью показать слабость в алгоритме AES., частично из-за невысокой сложности его нелинейных составляющих. С тех пор другие документы показали, что атака в том виде, в котором она была представлена изначально, неосуществима; см. XSL-атака на блочные шифры.
В процессе выбора AES разработчики конкурирующих алгоритмов написали об алгоритме Риджндала: «Мы обеспокоены использованием [его]... в критически важных для безопасности приложениях». Однако в октябре 2000 года, в конце процесса выбора AES, Брюс Шнайер, разработчик конкурирующего алгоритма Twofish, написал, что, хотя, по его мнению, успешные академические атаки на Rijndael будут когда-нибудь разработанная, он «не верил, что кто-либо когда-либо обнаружит атаку, которая позволит кому-то читать трафик Rijndael».
До мая 2009 года единственными успешными опубликованными атаками против полной AES были побочные атаки. канальные атаки на некоторые конкретные реализации. В 2009 году была обнаружена новая атака связанных ключей, которая использует простоту расписания ключей AES и имеет сложность 2. В декабре 2009 года она была улучшена до 2. Это последующая атака. обнаружен ранее в 2009 году Алексом Бирюковым, Дмитрием Ховратовичем и Ивицей Николичем, со сложностью 2 для одного из каждых 2 ключей. Однако атаки со связанными ключами не вызывают беспокойства ни в одном должным образом разработанном криптографическом протоколе, поскольку правильно разработанный протокол (т. Е. Программное обеспечение для реализации) позаботится о том, чтобы не допустить использование связанных ключей, по существу, ограничивая средства атакующего выбор ключей для родства.
Еще одна атака была опубликована в блоге Брюса Шнайера 30 июля 2009 г. и опубликована в виде препринта 3 августа 2009 г. Эта новая атака была создана Алексом Бирюковым, Орром Дункельманом, Натаном Келлером, Дмитрием Ховратовичем и Ади Шамир, против AES-256, который использует только два связанных ключа и 2 раза для восстановления полного 256-битного ключа 9-раундовой версии или 2 раза для 10-раундовой версии с более сильным типом связанная атака подключей, или 2 раза для 11-раундовой версии. 256-битный AES использует 14 раундов, поэтому эти атаки не эффективны против полного AES.
Практичность этих атак с более сильными связанными ключами подверглась критике, например, в статье об атаках с выбранным ключом-посредником на AES-128, автором которой является Винсент Раймен в 2010 году.
В ноябре 2009 года в качестве препринта была выпущена первая атака с распознаванием известного ключа против сокращенной 8-раундовой версии AES-128. Эта атака с распознаванием известного ключа является улучшением отскока или атаки начала с середины против AES-подобных перестановок, которые рассматривают два последовательных раунда перестановки как применение так называемого Super-S-блока.. Он работает с 8-раундовой версией AES-128, с временной сложностью 2 и сложностью памяти 2. 128-битный AES использует 10 раундов, поэтому эта атака не эффективна против полного AES-128.
Первые атаки с восстановлением ключа на полную AES были предприняты Андреем Богдановым, Дмитрием Ховратовичем и Кристианом Рехбергером и были опубликованы в 2011 году. Атака представляет собой бикликовую атаку и быстрее грубой силы примерно в четыре раза. Для восстановления ключа AES-128 требуется 2 операции. Для AES-192 и AES-256 необходимо 2 и 2 операции соответственно. Этот результат был дополнительно улучшен до 2 для AES-128, 2 для AES-192 и 2 для AES-256, которые на данный момент являются лучшими результатами атаки восстановления ключа против AES.
Это очень небольшой выигрыш, так как 126-битный ключ (вместо 128-битного) все равно потребует миллиарды лет, чтобы перебрать текущее и ожидаемое оборудование. Кроме того, авторы вычисляют лучшую атаку, используя свою технику на AES со 128-битным ключом, требующим хранения 2 бита данных. Это составляет около 38 триллионов терабайт данных, что больше, чем все данные, хранящиеся на всех компьютерах на планете в 2016 году. Таким образом, нет никаких практических последствий для безопасности AES. Позднее сложность пространства была увеличена до 2 бит, что составляет 9007 терабайт.
Согласно документам Сноудена, АНБ исследует, может ли криптографическая атака, основанная на тау-статистике, взломать AES.
В настоящее время не существует известной практической атаки, которая позволила бы кому-либо, не знающему ключа, читать данные, зашифрованные AES, при правильной реализации.
Атаки по побочному каналу не атакуют шифр как черный ящик и, таким образом, не связаны с безопасностью шифра, как определено в классическом контексте., но важны на практике. Они атакуют реализации шифра на аппаратном или программном обеспечении, в результате чего происходит непреднамеренная утечка данных. Известно несколько таких известных атак на различные реализации AES.
В апреле 2005 г. Д.Дж. Бернштейн объявил об атаке с синхронизацией кеша, которую он использовал для взлома специального сервера, который использовал шифрование AES OpenSSL. Для атаки потребовалось более 200 миллионов выбранных открытых текстов. Пользовательский сервер был разработан так, чтобы выдавать как можно больше информации о времени (сервер сообщает количество машинных циклов, затраченных на операцию шифрования). Однако, как указал Бернштейн, «уменьшение точности временных меток сервера или их исключение из ответов сервера не останавливает атаку: клиент просто использует время приема-передачи, основанное на своих локальных часах, и компенсирует повышенный шум. путем усреднения по большему количеству выборок ».
В октябре 2005 года Даг Арне Освик, Ади Шамир и Эран Тромер представили документ, демонстрирующий несколько атак с синхронизацией кеша на реализации в AES, найденных в OpenSSL и функции шифрования раздела dm-cryptLinux. Одна атака смогла получить весь ключ AES всего после 800 операций, запускающих шифрование, в общей сложности за 65 миллисекунд. Эта атака требует, чтобы злоумышленник имел возможность запускать программы в той же системе или платформе, на которой выполняется AES.
В декабре 2009 года была опубликована атака на некоторые аппаратные реализации, которая использовала дифференциальный анализ неисправностей и позволяет восстановить ключ со сложностью 2.
В ноябре 2010 года Endre Бангертер, Дэвид Гуллаш и Стефан Кренн опубликовали статью, в которой описал практический подход к восстановлению секретных ключей из AES-128 «почти в реальном времени» без необходимости в зашифрованном или открытом тексте. Этот подход также работает с реализациями AES-128, которые используют таблицы сжатия, такие как OpenSSL. Как и некоторые предыдущие атаки, для этой атаки требуется возможность запускать непривилегированный код в системе, выполняющей шифрование AES, что может быть достигнуто путем заражения вредоносным ПО гораздо проще, чем реквизиции учетной записи root.
В марте 2016 года Ashokkumar C., Рави Пракаш Гири и Бернард Менезеш представили атаку побочного канала на реализации AES, которая может восстановить полный 128-битный ключ AES всего за 6-7 блоков открытого текста / зашифрованного текста, что является существенным улучшением по сравнению с предыдущими работами, которые требовали от 100 до миллион шифров. Предлагаемая атака требует стандартных прав пользователя, а алгоритмы извлечения ключей выполняются менее чем за минуту.
Многие современные процессоры имеют встроенные аппаратные инструкции для AES, которые защищают от атак по побочным каналам, связанных с синхронизацией.
Программа валидации криптографических модулей (CMVP) осуществляется совместно Национальным институтом стандартов и технологий (NIST) правительства США, отделом компьютерной безопасности и организацией безопасности связи (CSE) правительства Канады. Правительство США требует использования криптографических модулей, утвержденных в соответствии с NIST FIPS 140-2, для шифрования всех данных, имеющих классификацию «Конфиденциальные, но несекретные» (SBU) или выше. Из NSTISSP № 11, Национальная политика по обеспечению получения информации: «Продукты шифрования для защиты секретной информации будут сертифицированы NSA, а продукты шифрования, предназначенные для защиты конфиденциальной информации, будут сертифицированы в соответствии с NIST FIPS 140-2».
Правительство Канады также рекомендует использовать проверенные по FIPS 140 криптографические модули в несекретных приложениях своих ведомств.
Хотя публикация NIST 197 («FIPS 197») является уникальным документом, который описывает алгоритм AES, поставщики обычно обращаются к CMVP в соответствии с FIPS 140 и просят иметь несколько алгоритмов (например, Triple DES или SHA1 ) проверяется одновременно. Следовательно, редко можно найти криптографические модули, которые однозначно проверены FIPS 197, а сам NIST обычно не тратит время на то, чтобы перечислить проверенные модули FIPS 197 отдельно на своем общедоступном веб-сайте. Вместо этого проверка FIPS 197 обычно просто указывается как нотация «Утверждено FIPS: AES» (с конкретным номером сертификата FIPS 197) в текущем списке проверенных FIPS 140 криптографических модулей.
Программа проверки криптографических алгоритмов (CAVP) позволяет проводить независимую проверку правильности реализации алгоритма AES. Успешная проверка приводит к появлению в списке на странице проверок NIST. Это тестирование является предварительным условием для проверки модуля FIPS 140-2, описанной ниже. Однако успешная проверка CAVP никоим образом не означает, что криптографический модуль, реализующий алгоритм, безопасен. Криптографический модуль без проверки FIPS 140-2 или специального одобрения NSA не считается безопасным правительством США и не может использоваться для защиты государственных данных.
Проверка FIPS 140-2 является сложной задачей как технически, так и фискально. Существует стандартная батарея тестов, а также элемент проверки исходного кода, который необходимо пройти в течение нескольких недель. Стоимость проведения этих тестов в утвержденной лаборатории может быть значительной (например, более 30 000 долларов США) и не включает время, необходимое для написания, тестирования, документирования и подготовки модуля для проверки. После проверки модули должны быть повторно представлены и повторно оценены, если они каким-либо образом изменены. Это может варьироваться от простых обновлений документов, если функциональные возможности безопасности не изменились, до более существенного набора повторных проверок, если на функциональные возможности безопасности это изменение повлияло.
Тестовые векторы - это набор известных шифров для данного входа и ключа. NIST распределяет эталоны тестовых векторов AES как векторы теста известных ответов AES (KAT).
Критериями процесса выбора AES были высокая скорость и низкие требования к ОЗУ. В качестве выбранного алгоритма AES хорошо работает на широком спектре оборудования, от 8-битных смарт-карт до высокопроизводительных компьютеров.
На Pentium Pro для шифрования AES требуется 18 тактовых циклов на байт, что эквивалентно пропускной способности около 11 МБ / с для процессора 200 МГц.
На процессорах Intel Core i3 /i5 /i7 и AMD Ryzen, поддерживающих расширения набора инструкций AES-NI, пропускная способность может составлять несколько ГБ / с (даже более 10 ГБ / с).
 сдвигается влево по кругу на
сдвигается влево по кругу на  байт. Для 256-битного блока первая строка не изменяется, а сдвиг для второй, третьей и четвертой строк составляет 1, 3 и 4 байта соответственно - это изменение применяется только для шифра Rijndael при использовании с 256-битным блоком., поскольку AES не использует 256-битные блоки.
байт. Для 256-битного блока первая строка не изменяется, а сдвиг для второй, третьей и четвертой строк составляет 1, 3 и 4 байта соответственно - это изменение применяется только для шифра Rijndael при использовании с 256-битным блоком., поскольку AES не использует 256-битные блоки.