Неисправность

Количество возможных перестановок и нарушений n элементов. п! (n факториал) - количество n-перестановок; ! n (n субфакториал) - это количество нарушений - n-перестановок, при которых все n элементов меняют свои начальные места.

Таблица значений
$n\; \{\backslash \; displaystyle\; n\}$	Перестановки, $n!\; \{\backslash \; displaystyle\; n!\}$	Психология, $!\; п\; \{\backslash \; displaystyle!\; n\}$	$!\; п\; п!\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{!\; n\}\; \{n!\}\}\}$
0	1 = 1 × 10	1 = 1 × 10	= 1
1	1 = 1 × 10	0	= 0
2	2 = 2 × 10	1 = 1 × 10	= 0,5
3	6 = 6 × 10	2 = 2 × 10	≈0,33333 33333
4	24 = 2,4 × 10	9 = 9 × 10	= 0,375
5	120 = 1,20 × 10	44 = 4,4 × 10	≈0,36666 66667
6	720 = 7,20 × 10	265 = 2,65 × 10	≈0,36805 55556
7	5 040 ≈ 5,04 × 10	1854 ≈1,85 × 10	≈0,36785 71429
8	40320 ≈4,03 × 10	14 833 ≈1,48 × 10	≈0,36788 19444
9	362880 ≈3,63 × 10	133496 ≈1,33 × 10	≈0,36787 91887
10	3628800 ≈3,63 × 10	1334961 ≈1,33 × 10	≈0,36787 94643
11	39 916 800 ≈3,99 × 10	14 684570 ≈ 1,47 × 10	≈0,36787 94392
12	479001600 ≈4,79 × 10	176214841 ≈1,76 × 10	≈0,36787 94413
13	6 227 020 800 ≈6,23 × 10	2 290 792932 ≈2,29 × 10	≈0,36787 94412
14	87 178 291 200 ≈ 8,72 × 10	32 071 101049 ≈3,21 × 10	≈0,36787 94412
15	1307674368000 ≈1,31 × 10	481066515734 ≈4,81 × 10	≈0,36787 94412
16	20 922 789 888 000 ≈ 2,09 × 10	7 697 064 251 745 ≈7,70 × 10	≈0,36787 94412
17	355 687 428 096 000 ≈3,56 × 10	130 850 092 279 664 ≈1,31 × 10	≈0,36787 94412
18	6 402 373 705 728 000 ≈6,40 × 10	2 355 301 661 033 953 ≈2,36 × 10	≈0,36787 94412
19	121 645 100 408 832 000 ≈1,22 × 10	44750 731 559 645106 ≈4,48 × 10	≈0,36787 94412
20	2 432 902 008 176 640 000 ≈2,43 × 10	895 014 631 192 902 121 ≈8,95 × 10	≈0,36787 94412
21	51090 942 171 709 440 000 ≈5,11 × 10	18 795 307 255 050 944 540 ≈1,88 × 10	≈0,36787 94412
22	1 124 000 727 777 607 680 000 ≈1,12 × 10	413 496 759 611 120 779 881 ≈4,13 × 10	≈0,36787 94412
23	25 852016 738 884 976 640 000 ≈2,59 × 10	9 510 425 471 055 777 937 262 ≈9,51 × 10	≈0,36787 94412
24	620 448 401 733 239 439 360 000 ≈6,20 × 10	228 250 211 305 338 670 494 289 ≈2,28 × 10	≈0,36787 94412
25	15 511 210 043 330 985 984 000 000 ≈1,55 × 10	5 706255 282 633 466 762 357 224 ≈ 5,71 × 10	≈0,36787 94412
26	403291461 126 605 635 584 000 000 ≈4,03 × 10	148 362 637 348 470 135 821 287 825 ≈1,48 × 10	≈0,36787 94412
27	10 888 869 450 418 352 160 768 000 000 ≈1,09 × 10	4 005791208408693 667174771274 ≈4,01 × 10	≈0,36787 94412
28	304 888 344 611 713 860 501 504 000 000 ≈ 3,05 × 10	112 162 153 835 443 422 680 893595 673 ≈1,12 × 10	≈0,36787 94412
29	8 841 761 993 739 701 954 543 616 000 000 ≈8,84 × 10	3252702461227 859 257 745 914 274 516 ≈3,25 × 10	≈0,36787 94412
30	265 252 859 812 191 058 6 36 308 480 000 000 ≈2,65 × 10	97 581 073 836 835 777 732 377 428 235 481 ≈9,76 × 10	≈0,36787 94412

In комбинаторный математика, нарушение - это перестановка элементов набора, так что ни один элемент не появляется в исходной позиции. Другими словами, расстройство - это перестановка, которая не имеет фиксированных точек.

. Количество расстройств набора размера n известно как субфактор числа n или n-е <36.>число психического расстройства или n-е число де Монморта . Нотации для часто используемых субфакториалов включают! N, D n, d n или n¡.

Можно показать, что! N равно ближайшему целому числу к n ! / e, где n! обозначает факториал числа n, а e - число Эйлера.

Проблема подсчета неисправностей была впервые рассмотрена Пьером Раймоном де Монмортом в 1708 году; он решил ее в 1713 году, как и Николас Бернулли примерно в то же время.

• 1 Пример
• 2 Расстройства подсчета
  • 2.1 Вывод по принципу включения-исключения
• 3 Предел отношения нарушения к перестановке при приближении n к ∞
• 4 Обобщения
• 5 Вычислительные сложность
• 6 Ссылки
• 7 Внешние ссылки

Выделены 9 отклонений (из 24 вариантов)

Предположим, что профессор дал тест 4 студентам - A, B, C и D - и хочет, чтобы они оценивали тесты друг друга. Конечно, ни один студент не должен ставить оценку за свой тест. Сколькими способами профессор мог бы передать тесты студентам для выставления оценок, чтобы ни один студент не получил обратно свой тест? Из 24 возможных перестановок (4!) Для возврата тестов,

ABCD,	ABDC,	ACBD,	ACDB,	ADBC,	ADCB,
BACD,	BADC,	BCAD,	BCDA,	BDAC,	BDCA,
CABD,	CADB,	CBAD,	CBDA,	CDAB,	CDBA,
DABC,	DACB,	DBAC,	DBCA,	DCAB,	DCBA.

всего 9 неисправностей (показаны синим курсивом выше). В каждой другой перестановке этого набора из 4-х членов, по крайней мере, один ученик получает обратно свой тест (выделен жирным красным).

Другая версия проблемы возникает, когда мы спрашиваем количество способов, которыми n букв, адресованных разному человеку, могут быть помещены в n предварительно адресованных конвертов, чтобы ни одна буква не появлялась в конверте с правильным адресом.

Подсчет сбоев в наборе сводится к так называемой проблеме проверки шляпы, в которой учитывается количество способов, которыми n шляп (назовите их от h 1 до h n) могут быть возвращены n людям (P 1 через P n), так что шляпа возвращает его владельцу.

Каждый человек может получить любую из n - 1 головных уборов, которая ему не принадлежит. Вызов любой из тех, что P 1 получает h i, и рассмотрим владельца h i : P i получает либо P 1, h 1 или какой-нибудь другой. Соответственно, проблема разделяется на два возможных случая:

1. Piполучает шляпу, отличную от h 1. Этот случай эквивалентен решению задачи с n - 1 людьми и n - 1 головными уборами, потому что для каждого из n - 1 человека, кроме P 1, есть ровно одна шляпа из оставшихся n - 1 шляп, которые они могут не получить (для любого P j, кроме P i, непринятым является h j, а для P i это h 1).
2. Piполучает h 1. В этом случае проблема сводится к n - 2 человека и n - 2 шляпы.

Для каждой из n - 1 шляпы P 1 может получить, количество способов, которыми P 2,…, P n могут все получить шляпы, является суммой подсчетов для двух случаев. Это дает нам решение Задача проверки шляпы: алгебраически сформулировано, что число! n неисправностей набора из n элементов равно

$!\; n\; =\; (n\; -\; 1)\; (!\; (n\; -\; 1)\; +!\; (n\; -\; 2))\; \{\backslash \; displaystyle\; !\; n\; =\; (n-1)\; (\{!\; (n-1)\}\; +\; \{!\; (n-2)\})\}$,

где! 0 = 1 и! 1 = 0. Первые несколько значений! n - :

Число нарушений в наборе из n элементов (последовательность A000166 в OEIS ) для малых n

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13
! n	1	0	1	2	9	44	265	1,854	14,833	133,496	1,334,961	14,684,570	176,214,841	2,290,792,932

Существуют также различные другие (эквивалентные) выражения для! N:

$!\; п\; =\; п!\; \sum \; я\; знак\; равно\; 0\; N\; (-\; 1)\; я\; я!\; п\; \ge \; 0,\; \{\backslash \; Displaystyle!\; п\; =\; п!\; \backslash \; сумма\; \_\; \{я\; =\; 0\}\; ^\; \{п\}\; \{\backslash \; гидроразрыва\; \{(-1)\; ^\; \{я\}\}\; \{я!\}\},\; \backslash \; четырехъядерных\; п\; \backslash \; geq\; 0,\}$

$!\; п\; =\; \lfloor \; п!\; е\; \rceil \; =\; \lfloor \; п!\; е\; +\; 1\; 2\; \rfloor ,\; n\; \ge \; 1.\; \{\backslash \; displaystyle!\; n\; =\; \backslash \; left\; \backslash \; lfloor\; \{\backslash \; frac\; \{n!\}\; \{e\}\}\; \backslash \; right\; \backslash \; rceil\; =\; \backslash \; left\; \backslash \; lfloor\; \{\backslash \; frac\; \{n!\}\; \{e\}\; \}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; right\; \backslash \; rfloor,\; \backslash \; quad\; n\; \backslash \; geq\; 1.\}$

(где $\lfloor \; x\; \rceil \; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; lfloor\; x\; \backslash \; right\; \backslash \; rceil\}$- это ближайшая целочисленная функция, а $\lfloor \; x\; \rfloor \; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; lfloor\; x\; \backslash \; right\; \backslash \; rfloor\}$- функция пола )

Для любого целого n ≥ 1,

$!\; N\; =\; \{\lfloor \; n!\; E\; +\; r\; 1\; \rfloor ,\; n\; нечетно,\; r\; 1\; \in \; [0,\; 1\; 2],\; \lfloor \; n!\; E\; +\; r\; 2\; \rfloor ,\; n\; равно\; четное,\; r\; 2\; \in \; [1\; 3,\; 1].\; \{\backslash \; displaystyle!\; n\; =\; \{\backslash \; begin\; \{cases\}\; \backslash \; lfloor\; \{\backslash \; frac\; \{n!\}\; \{e\}\}\; +\; r\_\; \{1\}\; \backslash \; rfloor,\; n\; \{\backslash \; text\; \{\; нечетное\}\},\; \backslash \; quad\; \backslash \; r\_\; \{1\}\; \backslash \; in\; [0,\; \{\backslash \; frac\; \{1\}\; \{2\}\}],\; \backslash \backslash \backslash \; lfloor\; \{\backslash \; frac\; \{n!\}\; \{e\}\}\; +\; r\_\; \{2\}\; \backslash \; rfloor,\; n\; \{\backslash \; text\; \{is\; even\}\},\; \backslash \; quad\; r\_\; \{2\}\; \backslash \; in\; [\{\backslash \; frac\; \{1\}\; \{3\}\},\; 1].\; \backslash \; end\; \{cases\}\}\}$

Итак, для любого целого числа n ≥ 1, и для любого действительного числа r ∈ [1/3, 1/2]

$!\; n\; =\; \lfloor \; n!\; e\; +\; r\; \rfloor ,\; n\; \ge \; 1,\; r\; \in \; [1\; 3,\; 1\; 2].\; \{\; \backslash \; Displaystyle!\; N\; =\; \backslash \; left\; \backslash \; lfloor\; \{\backslash \; frac\; \{n!\}\; \{e\}\}\; +\; r\; \backslash \; right\; \backslash \; rfloor,\; \backslash \; quad\; \backslash \; n\; \backslash \; geq\; 1,\; \backslash \; quad\; r\; \backslash \; in\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{\; 3\}\},\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; right].\}$

Следовательно, поскольку e = 2.71828…, 1 / e ∈ [1/3, 1/2], то

$!\; п\; =\; \lfloor \; п!\; +\; 1\; е\; \rfloor ,\; n\; \ge \; 1,\; \{\backslash \; displaystyle!\; N\; =\; \backslash \; left\; \backslash \; lfloor\; \{\backslash \; frac\; \{n!\; +1\}\; \{e\}\}\; \backslash \; right\; \backslash \; rfloor,\; \backslash \; quad\; \backslash \; n\; \backslash \; geq\; 1,\}$

$!\; п\; знак\; равно\; \lfloor \; (е\; +\; е\; -\; 1)\; п!\; \rfloor \; -\; \lfloor \; e\; n!\; \rfloor ,\; n\; \ge \; 2,\; \{\backslash \; displaystyle!\; N\; =\; \backslash \; left\; \backslash \; lfloor\; (e\; +\; e\; ^\; \{-\; 1\})\; n!\; \backslash \; Right\; \backslash \; rfloor\; -\; \backslash \; lfloor\; en!\; \backslash \; Rfloor,\; \backslash \; quad\; n\; \backslash \; geq\; 2,\}$

$!\; п\; =\; п!\; -\; \sum \; я\; знак\; равно\; 1\; N\; (N\; я)\; \cdot !\; (п\; -\; я),\; п\; \ge \; 1.\; \{\backslash \; Displaystyle!\; п\; =\; п!\; -\; \backslash \; сумма\; \_\; \{я\; =\; 1\}\; ^\; \{п\}\; \{п\; \backslash \; выбрать\; я\}\; \backslash \; cdot\; \{!\; (ni)\},\; \backslash \; квад\; \backslash \; п\; \backslash \; geq\; 1.\}$

Также выполняется следующее рекуррентное равенство:

$!\; п\; знак\; равно\; N\; (!\; (п\; -\; 1))\; +\; (-\; 1)\; п,\; п\; \ge \; 1.\; \{\backslash \; Displaystyle!\; п\; =\; п\; \backslash \; влево\; (!\; (п-1)\; \backslash \; вправо)\; +\; (-\; 1)\; ^\; \{п\},\; \backslash \; quad\; \backslash \; n\; \backslash \; geq\; 1.\}$

Вывод по принципу включения-исключения

Другой вывод (эквивалентной) формулы для количества нарушений n-множества выглядит следующим образом. Для $1\; \le \; k\; \le \; n\; \{\backslash \; displaystyle\; 1\; \backslash \; leq\; k\; \backslash \; leq\; n\}$мы определяем $S\; k\; \{\backslash \; displaystyle\; S\_\; \{k\}\}$как набор перестановок из n объектов, фиксирующих k-й объект. Любое пересечение набора i этих наборов фиксирует конкретный набор объектов i и, следовательно, содержит $(n\; -\; i)!\; \{\backslash \; displaystyle\; (n-i)!\}$перестановки. Существует $(n\; i)\; \{\backslash \; displaystyle\; \{n\; \backslash \; choose\; i\}\}$таких коллекций, поэтому принцип включения-исключения дает

, и поскольку нарушение - это перестановка, при которой ни один из n объектов не остается фиксированным, мы получаем

$!\; п\; =\; п!\; -\; |\; S\; 1\; \cup \; \cdots \; \cup \; S\; n\; |\; =\; п!\; \sum \; я\; знак\; равно\; 0\; N\; (-\; 1)\; я\; я!.\; \{\backslash \; displaystyle!\; n\; =\; n!\; -\; |\; S\_\; \{1\}\; \backslash \; cup\; \backslash \; cdots\; \backslash \; cup\; S\_\; \{n\}\; |\; =\; n!\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{n\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{\; i\}\}\; \{i!\}\}.\}$

От

$!\; п\; =\; п!\; \sum \; я\; знак\; равно\; 0\; N\; (-\; 1)\; я\; я!\; \{\backslash \; displaystyle!\; n\; =\; n!\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{n\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{i\}\}\; \{i!\}\}\}$

и

$ex\; =\; \sum \; i\; =\; 0\; \infty \; xii!\; \{\backslash \; displaystyle\; e\; ^\; \{x\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{x\; ^\; \{i\}\; \backslash \; over\; i!\}\}$

сразу получается, используя x = −1:

$lim\; п\; \to \; \infty !\; п\; п!\; =\; 1\; e\; \approx \; 0,3679\dots .\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{n\; \backslash \; to\; \backslash \; infty\}\; \{!\; n\; \backslash \; over\; n!\}\; =\; \{1\; \backslash \; over\; e\}\; \backslash \; приблизительно\; 0,3679\; \backslash \; ldots.\}$

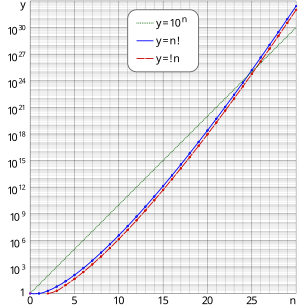
Это предел вероятности что случайно выбранная перестановка большого количества объектов - это нарушение. Вероятность очень быстро сходится к этому пределу с увеличением n, поэтому! N - ближайшее целое число к n! / E. Приведенный выше график semi-log показывает, что график неисправности отстает от графика перестановок почти на постоянное значение.

Дополнительную информацию об этом вычислении и указанном выше пределе можно найти в статье о статистике случайных перестановок.

Проблема рендеринга спрашивает, сколько перестановок набора размера n имеют ровно k неподвижных точек.

Расстройства - это пример более широкого поля ограниченных перестановок. Например, в задаче мужчин задается вопрос, сидят ли n пар противоположного пола мужчина-женщина-мужчина-женщина -... вокруг стола, сколькими способами они могут сидеть так, чтобы рядом никого не было. его или ее партнер?

Более формально, учитывая множества A и S и некоторые множества U и V из сюръекций A → S, мы часто хотим знать количество пар функций (f, g) таких что f находится в U, а g находится в V, и для всех a из A, f (a) ≠ g (a); другими словами, где для любых f и g существует расстройство φ группы S такое, что f (a) = φ (g (a)).

Еще одно обобщение - следующая проблема:

Сколько существует анаграмм без фиксированных букв данного слова?

Например, для слова, состоящего только из двух разных букв, скажем, n букв A и m букв B, ответ, конечно же, 1 или 0 в зависимости от того, n = m или нет, поскольку единственный способ сформировать анаграмму без фиксированных букв - это поменять все буквы A на B, что возможно тогда и только если n = m. В общем случае для слова из n 1 букв X 1, n 2 букв X 2,..., n r букв X r оказывается (после правильного использования формулы включение-исключение ), что ответ имеет вид:

$\int \; 0\; \infty \; П\; N\; 1\; (Икс)\; п\; N\; 2\; (Икс)\; \cdots \; П\; NR\; (Икс)\; е\; -\; xdx,\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; P\_\; \{n\_\; \{1\}\}\; (x)\; P\_\; \{n\_\; \{\; 2\}\}\; (x)\; \backslash \; cdots\; P\_\; \{n\_\; \{r\}\}\; (x)\; e\; ^\; \{-\; x\}\; \backslash ,\; dx,\}$

для некоторой последовательности многочленов P n, где P n имеет степень n. Но приведенный выше ответ для случая r = 2 дает соотношение ортогональности, откуда P n - это многочлены Лагерра (до знак, который легко решается).

$\int \; 0\; \infty \; (t\; -\; 1)\; ze\; -\; tdt\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; (t-1)\; ^\; \{z\}\; e\; ^\; \{-\; t\}\; dt\}$в комплексной плоскости.

В частности, для классических нарушений

$!\; N\; знак\; равно\; \int \; 0\; \infty \; (Икс\; -\; 1)\; N\; E\; -\; Икс\; Д\; Икс.\; \{\backslash \; displaystyle!\; n\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; (x-1)\; ^\; \{n\}\; e\; ^\; \{-\; x\}\; dx.\}$

Это NP-complete, чтобы определить, содержит ли данная группа перестановок (описываемая заданным набором перестановок, которые ее генерируют) какие-либо нарушения.

Найдите derangement в Wiktionary, бесплатном словаре.

• Баэз, Джон (2003). «Давайте психовать!» (PDF).
• Богарт, Кеннет П.; Дойл, Питер Г. (1985). «Несексистское решение проблемы мужчин и женщин».
• Дикау, Роберт М. «Диаграммы психических расстройств». Математические фигуры с использованием системы Mathematica.
• Хассани, Мехди. «Дефекты и приложения». Журнал целочисленных последовательностей (JIS), том 6, выпуск 1, статья 03.1.2, 2003 г.
• Вайсштейн, Эрик В.. "Психология". MathWorld - веб-ресурс Wolfram.