Войти
В математике и вычислениях, шестнадцатеричная (также основание 16 или шестнадцатеричная ) система счисления - это позиционная система счисления, которая представляет число с использованием системы счисления (основание) из 16. В отличие от обычного способа представления чисел с помощью 10 символов, шестнадцатеричный использует 16 различных символов, чаще всего символы «0» - «9» для представлений значений от 0 до 9, а « A »-« F »(или альтернативно« a »-« f ») для представления значений от 10 до 15.
Шестнадцатеричные числа широко используются разработчиками компьютерных систем и программистами, поскольку они обеспечивают удобное для человека представление двоично-кодированные значения. Каждая шестнадцатеричная цифра представляет собой четыре бита (двоичные цифры), также известные как полубайт (или полубайт), который составляет половину байта. Например, один байт может иметь значения от 00000000 до 11111111 в двоичной форме, которые можно удобно представить как от 00 до FF в шестнадцатеричной системе.
В математике для указания основания обычно используется нижний индекс. Например, десятичное значение 17,456 будет выражено в шестнадцатеричном виде как 4430 16. В программировании для обозначения шестнадцатеричных чисел используется ряд обозначений, обычно с префиксом или суффиксом. Префикс 0xиспользуется в C и родственных языках программирования, что обозначает это значение как 0x4430.
Шестнадцатеричное используется в кодировке передачи Base16, в котором каждый байт открытого текста разбит на два 4-битных значения и представлен двумя шестнадцатеричными цифрами.
| 0шестнадцатеричное | = | 0десятичное | = | 0окт | 0 | 0 | 0 | 0 | |
| 1шестнадцатеричное | = | 1dec | = | 1oct | 0 | 0 | 0 | 1 | |
| 2hex | = | 2dec | = | 2oct | 0 | 0 | 1 | 0 | |
| 3hex | = | 3dec | = | 3oct | 0 | 0 | 1 | 1 | |
| 4hex | = | 4dec | = | 4oct | 0 | 1 | 0 | 0 | |
| 5hex | = | 5dec | = | 5oct | 0 | 1 | 0 | 1 | |
| 6hex | = | 6dec | = | 6oct | 0 | 1 | 1 | 0 | |
| 7hex | = | 7dec | = | 7oct | 0 | 1 | 1 | 1 | |
| 8hex | = | 8dec | = | 10oct | 1 | 0 | 0 | 0 | |
| 9hex | = | 9dec | = | 11oct | 1 | 0 | 0 | 1 | |
| Ahex | = | 10dec | = | 12oct | 1 | 0 | 1 | 0 | |
| Bhex | = | 11dec | = | 13oct | 1 | 0 | 1 | 1 | |
| Chex | = | 12dec | = | 14oct | 1 | 1 | 0 | 0 | |
| Dhex | = | 13dec | = | 15oct | 1 | 1 | 0 | 1 | |
| Ehex | = | 14dec | = | 16oct | 1 | 1 | 1 | 0 | |
| Fшестнадцатеричный | = | 15десятичный | = | 17октавный | 1 | 1 | 1 | 1 | |
шестнадцатеричный. Не существует универсального соглашения об использовании строчных или прописных букв, поэтому каждый из них является преобладающим или предпочтительным в определенных средах по стандартам или соглашению сообщества; часто используется даже смешанный регистр. Семисегментные дисплеи используют AbCdEF в смешанном регистре для создания цифр, которые можно отличить от друга.
В контекстах, где основание неясно, шестнадцатеричные числа могут быть неоднозначными и путаться с числами, выраженными в других основаниях. Есть несколько соглашений для однозначного выражения ценностей. Числовой индекс (сам записанный в десятичном формате) может явно указывать основание: 159 10 десятичное 159; 159 16 - шестнадцатеричное число 159, что равно 345 10. Некоторые авторы предпочитают текстовый индекс, например 159 десятичный и 159 шестнадцатеричный, или 159 d и 159 h.
Дональд Кнут ввел использование конкретного шрифта для представления определенного основания в его книге The TeXbook. Шестнадцатеричные представления записываются там шрифтом пишущей машинки: 5A3
В линейных текстовых системах, таких как те, которые используются в большинстве сред компьютерного программирования, возникло множество методов:
0xдля числовых констант, представленных в шестнадцатеричном формате: 0x5A3. Символьные и строковые константы могут выражать коды символов в шестнадцатеричном виде с префиксом \ x, за которыми следуют две шестнадцатеричные цифры: '\ x1B'представляет управляющий символ Esc ; "\ x1B [0m \ x1B [25; 1H"- строка, содержащая 11 символов с двумя встроенными символами Esc. Для вывода целого числа в шестнадцатеричном формате с помощью семейства функций printf используется код преобразования формата % Xили % x.%: http: // www.example.com / name% 20with% 20spaces, где % 20- это код для пробела (пробела) символов, ASCII кодовая точка 20 в шестнадцатеричный формат, 32 в десятичном.ode;, например 'представляет собой символ U + 2019 (правая одинарная кавычка). Если нет x, число является десятичным (таким образом, '- это тот же символ).U +, за которым следует шестнадцатеричное значение, например U + 20AC- знак евро (€).#: белый, например, представлен как #FFFFFF. CSS также допускает трехзначные сокращения с одной шестнадцатеричной цифрой на компонент: # FA3 сокращает # FFAA33 (золотой апельсин :).=: Espa = F1ais " España »(F1 - это код для наборе символов ISO / IEC 8859-1).FFhили 05A3H. В некоторых реализациях требуется начальный ноль, когда первый символ шестнадцатой цифры не является десятичной цифрой, поэтому можно было бы написать 0FFhвместо FFh$ 5A3.H ' ABCD '(для ABCD 16). Точно так же Fortran 95 использует Z'ABCD '.16 # 5A3 #. Для констант битовых векторов VHDL использует нотацию x "5A3".8'hFF, где 8 - количество бит в значении, а FF - шестнадцатеричная константа.16r: 16r5A316 #: 16 # 5A3. Для PostScript двоичные данные (например, изображение пикселей ) могут быть выражены как последовательные шестнадцатеричные пары без префикса: AA213FD51B3801043FBC...# xи # 16r. Установка числа * read-base * и * print-base * на 16 также может установить для переключения считывателя и системы принтера Common Lisp на шестнадцатеричное представление чисел для чтения и печати чисел. Таким образом, шестнадцатеричные числа могут быть представлены без префикса #x # 16r, когда база ввода или вывода была изменена на 16.H: H5A30h: 0h5A316rдля обозначения шестнадцатеричных чисел: 16r5a3. Аналогичным образом можно указать двоичные, четвертичные (base-4) и восьмеричные числа.X'5A3 'и используется в Ассемблере, PL / I, COBOL, JCL, скриптах, командах и других местах. Этот формат был распространен и на других (уже устаревших) систем IBM. Иногда вместо апострофов использовались кавычки.:). Это, например, действующий IPv6-адрес: 2001: 0db8: 85a3: 0000: 0000: 8a2e: 0370: 7334или сокращенный путем удаления нулей как 2001: db8: 85a3 :: 8a2e: 370: 7334(IPv4-адрес обычно записываются в десятичном формате).3F2504E0-4F89-41D3-9A0C-0305E82C3301.Использование букв от A до F для обозначения цифр выше 9 не было универсальным в ранней истории компьютеров.
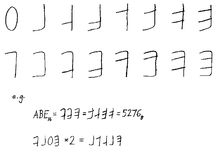Предложение Брюса Алана Мартина о шестнадцатеричной системе счисления Нет представлений цифр для представления величин от десяти до пятнадцати букв используются в заменах - и в европейских языках отсутствуют недесятичные имена для цифр выше десяти. Хотя на английском языке есть имена для нескольких недесятичных степеней (пара для первой двоичной степени, оценка для первой десятичной степени, дюжина, брутто и брутто для первых трех двенадцатеричных степеней), ни одно английское название не имеет шестнадцатеричные степени (десятичные 16, 256, 4096, 65536,...). Некоторые люди читают шестнадцатеричные числа цифру за цифрой, например номер телефона, или используют фонетический алфавит НАТО, Объединенный фонетический алфавит армии / флота или аналогичную специальную систему. После того, как программисты IBM System / 360 приняли шестнадцатеричный формат, Роберт А. Магнусон в 1968 году в журнале Datamation Журнал руководство по произношению, в котором краткие названия букв шестнадцатеричного числа - например, "A" произносится как "ann", B "ставка", C "chris" и т. д. Другая система именования была изобретена независимо Тимом Бэббом в 2015 году. Дополнительная система имен была опубликована в Интернете SR Rogers в 2007 году, которая старается сделать словесное представление различимым в любом случае, даже если действительное число не содержит чисел AF. Примеры приведены в таблицах ниже.
Шестнадцатеричная схема подсчета пальцев Системы подсчета по цифрам были разработаны как для двоичной, так и для шестнадцатеричной системы. Артур К. Кларк использует каждый палец как бит включения / выключения, позволяя подсчет пальцев от нуля до 1023 10 на десяти пальцах. Другая система для подсчета до FF 16 (255 10) справа.
| Число | Произношение |
|---|---|
| A | ann |
| B | bet |
| C | chris |
| D | dot |
| E | ernest |
| F | frost |
| 1A | annteen |
| A0 | аннти |
| 5B | пятьдесят-бет |
| A01C | аннти кристин |
| 1AD0 | аннтин дотти |
| 3A7D | тридцать лет семидесяти точек |
| Число | Произношение |
|---|---|
| C | двенадцать |
| F | fim |
| 11 | oneteek |
| 1F | fimteek |
| 50 | fiftek |
| C0 | twelftek |
| 100 | hundrek |
| 1000 | thousek |
| 3E | thirtek-eptwin |
| E1 | eptek-one |
| C4A | двенадцать-hundrek-fourtek-ten |
| 1743 | one-thousek-seven-hundrek-fourtek-three |
Шестнадцатеричная система может выражать отрицательные числа так же, как и в десятичной: -2A для представления -42 10 и так далее.
Шестнадцатеричный код инсталляционной установки для обозначения точных битовых шаблонов, используемый в языке, последовательность шестнадцатеричных цифр может представиться знаковый или даже с плавающей запятой. Таким образом, отрицательное число -42 10 может быть записано как FFFF FFD6 в 32-битном регистре ЦП (в с дополнением до двух ), как C228 0000 в 32-битном регистре FPU или C045 0000 0000 0000 в 64-битном регистре FPU (в стандарте IEEE с плавающей запятой ).
Как десятичные числа могут быть представлены в экспоненциальном представлении, так и шестнадцатеричные числа могут быть представлены. По соглашению, буква P (или p, что означает «степень») представляет собой умножение на две в степени, в то время как E (или e) служит той же целью в десятичной системе счисления как часть E-нотации. Число после P является десятичным и представляет двоичную экспоненту. Увеличение показателя степени на 1 умножается на 2, а не на 16. 10.0p1 = 8.0p2 = 4.0p3 = 2.0p4 = 1.0p5. Обычно нормализуется так, что ведущая шестнадцатеричная цифра равна 1 (если только значение не равно 0).
Пример: 1.3DEp42 представляет 1.3DE 16 × 2.
Шестнадцатеричная экспоненциальная запись требуется в соответствии с IEEE 754-2008 двоичной плавающей точки. стандарт. Эта нотация может установить для литералов с плавающей запятой в редакции C99 языка программирования C. Используя спецификаторы преобразования% a или% A, эта нотация может быть получена с помощью реализаций функций printf в соответствии со спецификацией C99 и Single Unix Specification (IEEE Std 1003.1) POSIX стандарт.
Большинство компьютеров манипулируют двоичными данными, но людям трудно работать с большим числом цифр даже для относительно небольшое двоичное число. Хотя большинство людей знакомы с системой с основанием 10 намного проще использовать двоичный код в шестнадцатеричный, чем в десятичный, потому что каждая шестнадцатая цифра соответствует целому количеству бит (4 10). В этом примере 1111 2 преобразуется в десятичное. Каждую позицию в двоичном числе может быть либо 1, либо 0, его значение может быть легко определено по его положению справа:
Следовательно:
| 1111 2 | = 8 10 + 4 10 + 2 10 + 1 10 |
| = 15 10 |
С небольшой практикой сопоставление 1111 2 с F 16 за один шаг становится проще: см. Таблицу в письменном представлении. Преимущество использования шестнадцатеричного числа, а не десятичного, быстро возрастает с преимуществом размера числа. Когда число становится большим, преобразование в десятичном становится очень утомительным. Однако при отображении в шестнадцатеричный формат двоичную тривиально рассматривать как группу из 4 цифр и отображать каждую в одну шестнадцатеричную цифру.
В этом примере показано преобразование двоичного числа в десятичное, отображение каждой цифры в десятичном значении и сложение результатов.
| (01011110101101010010) 2 | = 262144 10 + 65536 10 + 32768 10 + 16384 10 + 8192 10 + 2048 10 + 512 10 + 256 10 + 64 10 + 16 10 + 2 10 |
| = 387922 10 |
это преобразование в шестнадцатеричное, где каждую группу из четырех цифр можно рассматривать и независимо преобразовывать напрямую:
| (01011110101101010010) 2 | = | 0101 | 1110 | 1011 | 0101 | 0010 2 |
| = | 5 | E | B | 5 | 216 | |
| = | 5EB52 16 | |||||
Преобразование из шестнадцатеричного в двоичное также осуществляется напрямую.
Хотя четвертичный (с основанием 4) мало используется, его можно легко преобразовать в шестнадцатеричный или двоичный формат и обратно. Каждая шестнадцатеричная цифра соответствует паре четвертичных цифр, а каждая четвертичная цифра соответствует паре двоичных цифр. В приведенном выше примере 5 EB 5 2 16 = 11 32 23 11 02 4.
Восьмеричная система (с основанием 8) также может быть преобразована с относительной легкостью, хотя и не так тривиально. как с основаниями 2 и 4. Каждая восьмеричная цифра соответствует трем двоичным цифрам, а не четырем. Следовательно, мы можем преобразовать восьмеричное и шестнадцатеричное числа с помощью промежуточного преобразования в двоичное с последующей перегруппировкой двоичных цифр в группы по три или четыре.
Как и для всех баз, существует простой алгоритм для преобразования представления числа в шестнадцатеричном процессе выполнения целочисленных операций деления и остатка в исходной базе. Теоретически это возможно с любыми базами, но с помощью этого метода можно легко вычислить только методы двоичного числа, которые могут быть преобразованы только с помощью любого метода (которые можно преобразовать гораздо более эффективными методами).
Пусть d будет численным, которое нужно представить в шестнадцатеричном формате, а ряд h ihi-1... h 2h1будет шестнадцатеричными цифрами, представляющими число.
«16» может быть заменено любой другой базой, которая может быть желательной.
Ниже представлена реализация JavaScript вышеуказанного алгоритма для преобразования любого числа в шестнадцатеричное в строковом представлении. Его цель - проиллюстрировать описанный выше алгоритм. Однако для серьезной работы с данными гораздо более целесообразно работать с побитовыми операторами.
функция toHex (d) {var r = d% 16; если (d - r == 0) {вернуться кChar (r); } return toHex ((d - r) / 16) + toChar (r); } функция toChar (n) {const alpha = "0123456789ABCDEF"; вернуть alpha.charAt (n); }
Шестнадцатеричная таблица умножения Также возможно выполнить преобразование, присвоив каждому месту в исходной базе шестнадцатеричное представление его значения разряда - перед выполнением умножения и дополнение, чтобы получить окончательное представление. Например, чтобы преобразовать число B3AD в десятичное, можно разделить шестнадцатеричное число на его цифры: B (11 10), 3 (3 10), A (10 10) и D (13 10), а затем получите окончательный результат, умножившее представление на 16 (соответствующая позиция шестнадцатеричной цифры, считая справа налево, начиная с 0). В этом случае мы имеем следующее:
B3AD = (11 × 16) + (3 × 16) + (10 × 16) + (13 × 16)
, что составляет 45997 в базе 10.
Большинство современных компьютерных систем с графическим пользовательским интерфейсом использует встроенную утилиту калькулятора, способную выполнить преобразование между различными основами, и в большинстве случаев также будут учитываться шестнадцатеричный.
В Microsoft Windows утилиту Калькулятор можно установить в научный режим (в некоторых версиях он называется режимом программиста), который позволяет выполнять преобразование между основанием 16 (шестнадцатеричным), 10 (десятичное), 8 (восьмеричное ) и 2 (двоичное ), основы, наиболее часто используемые программистами. В научном режиме экранная цифровая клавиатура включает шестнадцатеричные цифры от A до F, которые активны, когда выбрано "Hex". Однако в шестнадцатеричном режиме калькулятор Windows поддерживает только целые числа.
Элементарные операции, такие как сложение, вычитание, умножение и деление, производимое косвенным путем преобразования в альтернативную систему счисления, такую как обычно используемую десятичную систему. системе или двоичной системе, где каждая шестнадцатеричная цифра соответствует четырем двоичным цифрам.
В качестве альтернативы, можно также выполнять элементы непосредственно внутри самой шестнадцатеричной системы - полагаться на ее таблицы сложения / умножения и соответствующие стандартные алгоритмы, такие как деление в столбик и алгоритм вычитания.
Как и в других системах счисления, шестнадцатеричная система может представить для представления рациональных чисел, хотя повторяется расширения распространены, поскольку шестнадцать (10 16) имеют только один простой множитель; два.
Для любого основания 0,1 (или "1/10") всегда эквивалентно единице, деленной на представлении этого базового значения в его собственной системе счисления. Таким образом, будь то деление единицы на два для двоичного кода или деление единицы на шестнадцать для шестнадцатеричного, обе эти дроби записываются как 0,1. Механиание системы счисления 16 является точным квадратом (4), дроби, выраженные в шестнадцатеричном формате, имеют нечетный период чаще, чем десятичные, и не существует циклических чисел (кроме тривиальных одиночных цифр)). Повторяющиеся цифры, когда знаменатель в младших членах имеет простой множитель, не найденный в системе счисления; таким образом, при использовании шестнадцатеричной записи все дроби со знаменателями, не являющимися степенью двойки, приводят к бесконечной строке повторяющихся цифр (например, третей и пятых). Это делает шестнадцатеричное (и двоичное) менее, чем десятичное для представления рациональных чисел, поскольку большая часть лежит за пределами диапазона конечного представления.
Все рациональные числа, конечно представимые в шестнадцатеричном формате, также могут быть конечно представлены в десятичном, двенадцатеричном и шестидесятеричном : то есть любое шестнадцатеричное число с конечным числом цифр также имеет конечное число цифр, выраженное в этих других основаниях. И наоборот, только часть тех, которые конечно представимы в последних базисах, конечно представима в шестнадцатеричной системе счисления. Например, десятичное число 0,1 соответствует бесконечному повторяющемуся представлению 0,19 в шестнадцатеричном формате. Однако шестнадцатеричный формат более эффективен, чем двенадцатеричный и шестидтеричный для дробей со степенью двойки в знаменателе. Например, 0,0625 10 (одна шестнадцатая) эквивалентно 0,1 16, 0,09 12 и 0; 3,45 60.
| n | десятичное. Простые множители основания, b = 10: 2, 5; б - 1 = 9: 3; b + 1 = 11: 11 | Шестнадцатеричный. Простые множители основания, b = 16 10 = 10: 2; b - 1 = 15 10 = F: 3, 5; b + 1 = 17 10 = 11: 11 | ||||
|---|---|---|---|---|---|---|
| Дробь | Простые множители | Позиционное представление | Позиционное представление | Основные множители | Дробь (1 / n) | |
| 2 | 1/2 | 2 | 0,5 | 0,8 | 2 | 1/2 |
| 3 | 1/3 | 3 | 0.3333... = 0.3 | 0.5555... = 0.5 | 3 | 1/3 |
| 4 | 1/4 | 2 | 0,25 | 0,4 | 2 | 1/4 |
| 5 | 1/5 | 5 | 0,2 | 0.3 | 5 | 1/5 |
| 6 | 1/6 | 2, 3 | 0,1 6 | 0,2 A | 2, 3 | 1/6 |
| 7 | 1/7 | 7 | 0.142857 | 0.249 | 7 | 1/7 |
| 8 | 1/8 | 2 | 0,125 | 0,2 | 2 | 1/8 |
| 9 | 1/9 | 3 | 0.1 | 0.1C7 | 3 | 1/9 |
| 10 | 1/10 | 2, 5 | 0,1 | 0,1 9 | 2, 5 | 1 / A |
| 11 | 1/11 | 11 | 0.09 | 0.1745D | B | 1 / B |
| 12 | 1/12 | 2, 3 | 0,08 3 | 0,1 5 | 2, 3 | 1 / C |
| 13 | 1/13 | 13 | 0.076923 | 0.13B | D | 1 / D |
| 14 | 1/14 | 2, 7 | 0,0 714285 | 0,1 249 | 2, 7 | 1 / E |
| 15 | 1/15 | 3, 5 | 0,0 6 | 0.1 | 3, 5 | 1 / F |
| 16 | 1/16 | 2 | 0,0625 | 0,1 | 2 | 1/10 |
| 17 | 1/17 | 17 | 0.0588235294117647 | 0.0F | 11 | 1/11 |
| 18 | 1/18 | 2, 3 | 0,0 5 | 0,0 E38 | 2, 3 | 1/12 |
| 19 | 1/19 | 19 | 0.052631578947368421 | 0.0D79435E5 | 13 | 1/13 |
| 20 | 1/20 | 2, 5 | 0,05 | 0,0 C | 2, 5 | 1/14 |
| 21 | 1/21 | 3, 7 | 0.047619 | 0.0C3 | 3, 7 | 1/15 |
| 22 | 1/22 | 2, 11 | 0,0 45 | 0,0 BA2E8 | 2, B | 1/16 |
| 23 | 1/23 | 23 | 0.0434782608695652173913 | 0.0B21642C859 | 17 | 1 / 17 |
| 24 | 1/24 | 2, 3 | 0,041 6 | 0,0 A | 2, 3 | 1/18 |
| 25 | 1/25 | 5 | 0,04 | 0.0A3D7 | 5 | 1/19 |
| 26 | 1/26 | 2, 13 | 0,0 384615 | 0,0 9D8 | 2, D | 1 / 1A |
| 27 | 1/27 | 3 | 0.037 | 0.097B425ED | 3 | 1 / 1B |
| 28 | 1/28 | 2, 7 | 0,03 571428 | 0,0 924 | 2, 7 | 1 / 1C |
| 29 | 1/29 | 29 | 0.0344827586206896551724137931 | 0.08D3DCB | 1D | 1 / 1D |
| 30 | 1/30 | 2, 3, 5 | 0,0 3 | 0,0 8 | 2, 3, 5 | 1 / 1E |
| 31 | 1/31 | 31 | 0.032258064516129 | 0.08421 | 1F | 1 / 1F |
| 32 | 1/32 | 2 | 0,03125 | 0,08 | 2 | 1/20 |
| 33 | 1/33 | 3, 11 | 0.03 | 0.07C1F | 3, B | 1/21 |
| 34 | 1/34 | 2, 17 | 0,0 29411 76470588235 | 0,0 78 | 2, 11 | 1/22 |
| 35 | 1/35 | 5, 7 | 0,0 285714 | 0.075 | 5, 7 | 1 / 23 |
| 36 | 1/36 | 2, 3 | 0,02 7 | 0,0 71C | 2, 3 | 1/24 |
В таблице ниже приведены расширения некоторых распространенных иррациональных чисел в десятичном и шестнадцатеричном формате.
| Число | Позиционное представление | |||
|---|---|---|---|---|
| Десятичное | Шестнадцатеричное | |||
| √2 (длина диагонали единицы квадрата ) | 1.414213562373095048... | 1.6A09E667F3BCD... | ||
| √3 (длина диагонали единицы куб ) | 1.732050807568877293... | 1.BB67AE8584CAA... | ||
| √5 (длина диагонали прямоугольника 1 × 2 ) | 2.236067977499789696... | 2.3C6EF372FE95... | ||
| φ (phi, золотое сечение = (1 + √5) / 2) | 1.618033988749894848... | 1.9E3779B97F4A... | ||
| π (пи, отношение окружности <От 28>до диаметра окружности) | 3,141592653589793238462643. 383279502884197169399375105... | 3.243F6A8885A308D313198A2E0. 370734499F401D0938 натуральный логарифм <61817399... 506>(константа Туэ - Морса ) | 0,412454033640107597... | 0,6996 9669 9669 6996... |
| γ (предельная разница между. гармонический ряд и натура льный логарифм) | 0,577215664901532860... | 0,93C467E37DB0C7A4D1B... | ||
Полномочия два имеют очень простые расширения в шестнадцатеричном формате. Первые шестнадцать степеней двойки ниже показаны.
| 2 | Значение | Значение (десятичное) |
|---|---|---|
| 2 | 1 | 1 |
| 2 | 2 | 2 |
| 2 | 4 | 4 |
| 2 | 8 | 8 |
| 2 | 10шестнадцатеричное | 16десятичное |
| 2 | 20шестнадцатеричное | 32десятичное |
| 2 | 40шестнадцатеричное | 64десятичное |
| 2 | 80шестнадцатеричное | 128 десятичное |
| 2 | 100 шестнадцатеричный | 256 десятичный |
| 2 | 200 шестнадцатеричный | 512 десятичный |
| 2 (2) | 400 шестнадцатеричный | 1024 десятичное |
| 2 (2) | 800 шестнадцатеричное | 2048 десятичное |
| 2 (2) | 1000 шестнадцатеричный | 4096 десятичный |
| 2 (2) | 2000 шестнадцатеричный | 8192 десятичный |
| 2 (2) | 4000 шестнадцатеричный | 16,384 десятичный |
| 2 (2) | 8000 шестнадцатеричный | 32,768 десятичный |
| 2 (2) | 10000 шестнадцатеричный | 65,536 десятичный |
Слово шестнадцатеричное состоит из шестнадцатеричного числа, образованного от греческого ἕξ (шестнадцатеричный) для шести и -десятичный, производный от латинского для десятого. В онлайн-издании «Третий новый интернационал Вебстера» шестнадцатеричные числа выводятся как разновидность латинских шестнадцатеричных чисел (которые включают в более ранней документации Bendix). Самая ранняя дата, засвидетельствованная для шестнадцатеричного числа в Merriam-Webster Collegiate онлайн - 1954 год, что безопасно помещает его в категорию международного научного словаря (ISV). В ISV принято свободно смешивать греческий и латинский , комбинируя формы. Слово шестидесятеричный (для основания 60) сохрани латинский префикс. Дональд Кнут указал, что этимологически правильный термин - это старческий (или, возможно, седельный), от латинского термина для сгруппированных по 16. (Термины двоичные, тройные и четвертичные используются той же латинской конструкции, и Этимологически правильные) термины для десятичной и восьмеричной арифметики - денарная и восьмеричная соответственно.) Альфред Б. Тейлор использовал старшую систему в своей работе середины 1800-х годов по альтернативным основам счисления, хотя он отклонил основание 16 из-за его «непостоянного количества цифр». Шварцман отмечает, что ожидаемая форма от обычного латинского выражения будет шестнадцатеричной, но компьютерные хакеры будут сокращены это слово до пола. этимологически собственно греческим термином будет шестнадцатеричный / ἑξαδεκαδικός / hexadekadikós (хотя в новогреческом чаще используется decahexadic / δεκαεξαδικός / dekaexadikos).
Традиционными китайскими единицами измерения было основание-16. Например, один цзин (斤) в старой системе равенство шестнадцати таэлям. suanpan (китайский abacus ) можно использовать для выполнения шестнадцатеричных вычислений, таких как сложение и вычитание.
Как и двенадцатеричной системы, время от времени предпринимались попытки продвинуть шестнадцатеричную систему счисления в качестве предпочтительной. Эти часто определяют конкретное произношение и символы для отдельных цифр.
Пример унифицированных стандартных мер шестнадцатеричное время, в день делится на 16, так что в нем 16 "шестнадцатеричных часов" в день.
Base16 (как собственное имя без пробела) также может относиться к двоичному кодированию текста, принадлежащему к тому же семейству как Base32, Base58 и Base64.
В этом случае данные включаются на 4-битные последовательность, и каждое значение (от 0 до 15ительно) кодируется используя 16 символов из набора символов ASCII. Хотя можно использовать любые 16 символов из набора символов ASCII, на практике всегда выбираются цифры ASCII '0' - '9' и буквы 'A' - 'F' (или строчные 'a' - 'f'). для согласования со стандартной записью шестнадцатеричных чисел.
Существует несколько преимуществ кодировки Base16:
Поддержка кодирования Base16 повсеместно используется в современных вычислениях. Это основа для стандарта W3C для процентного кодирования URL, где символ заменяется знаком процента «%» и его форма в кодировке Base16. Большинство современных языков программирования напрямую включают поддержку форматирования и анализа чисел в кодировке Base16.
