68–95–99.7 правило - 68–95–99.7 rule

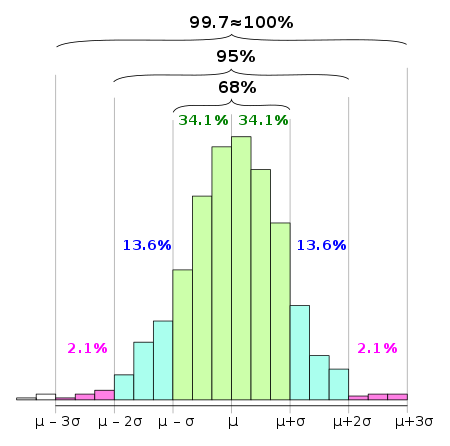
Сокращение, используемое в статистике Для примерно нормального набора данных значения в одно стандартное отклонение среднего составляет около 68% от набора; при этом в пределах двух стандартных отклонений приходится около 95%; и в пределах трех стандартных отклонений составляют около 99,7%. Показанные проценты представляют собой округленные теоретические вероятности, предназначенные только для приближения эмпирических данных, полученных из нормальной генеральной совокупности. Интервал прогноза (на оси y ), заданный из стандартной оценки (на ось x ). Ось Y масштабируется логарифмически (но значения на ней не изменяются).

В статистике применяется правило 68–95–99,7, также известное как эмпирическое правило - это сокращение, используемое для запоминания процентной доли значений, которые лежат в полосе вокруг среднего в нормальном распределении с шириной два, четыре и шесть стандартные отклонения соответственно; точнее, 68,27%, 95,45% и 99,73% значений лежат в пределах одного, двух и трех стандартных отклонений от среднего, соответственно.

В математической нотации эти факты можно выразить следующим образом, где Χ - это наблюдение нормально распределенной случайной величины, μ - среднее значение распределения, а σ - его стандартное отклонение:

$Pr\; (\mu \; -\; 1\; \sigma \; \le \; X\; \le \; \mu \; +\; 1\; \sigma )\; \approx \; 0,6827\; Pr\; (\mu \; -\; 2\; \sigma \; \le \; X\; \le \; \mu \; +\; 2\; \sigma )\; \approx \; 0,9545\; Pr\; (\mu \; -\; 3\; \sigma \; \le \; Икс\; \le \; \mu \; +\; 3\; \sigma )\; \approx \; 0,9973\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \backslash \; Pr\; (\backslash \; mu\; -1\; \backslash \; sigma\; \backslash \; leq\; X\; \backslash \; leq\; \backslash \; mu\; +1\; \backslash \; sigma)\; \backslash \; приблизительно\; 0,6827\; \backslash \backslash \backslash \; Pr\; (\backslash \; mu\; -2\; \backslash \; sigma\; \backslash \; leq\; X\; \backslash \; leq\; \backslash \; mu\; +2\; \backslash \; sigma)\; \backslash \; приблизительно\; 0,9545\; \backslash \backslash \backslash \; Pr\; (\backslash \; mu\; -3\; \backslash \; sigma\; \backslash \; leq\; X\; \backslash \; leq\; \backslash \; mu\; +3\; \backslash \; sigma)\; \backslash \; приблизительно\; 0,9973\; \backslash \; end\; \{align\}\}\}$

В эмпирических науках так называемое эмпирическое правило трех сигм выражает обычную эвристику, согласно которой почти все значения считаются лежащими в пределах трех стандартных отклонений от среднего, и поэтому эмпирически полезно рассматривать 99,7% вероятность как близкую к достоверности. Полезность этой эвристики особенно зависит от рассматриваемого вопроса. В социальных науках результат может считаться «значимым », если его уровень достоверности имеет порядок эффекта двух сигм (95%), в то время как в физике элементарных частиц существует соглашение о том, что эффект пяти сигм (достоверность 99,99994%) требуется для квалификации как открытие.

Более слабое правило трех сигм может быть получено из Неравенство Чебышева, утверждающее, что даже для переменных с ненормальным распределением по крайней мере 88,8% случаев должны попадать в правильно рассчитанные трехсигмовые интервалы. Для унимодальных распределений вероятность попадания в интервал составляет не менее 95% по неравенству Высочанского – Петунина. Для распределения могут быть определенные допущения, которые заставляют эту вероятность быть не менее 98%.

• 1 Кумулятивная функция распределения
• 2 Тесты нормальности
• 3 Таблица числовых значений
• 4 См. Также
• 5 Ссылки
• 6 Внешние ссылки

Диаграмма, показывающая кумулятивную функцию распределения для нормального распределения со средним (μ) 0 и дисперсией (σ) 1

Эти числовые значения «68%, 95%, 99,7%» получены из кумулятивной функции распределения нормального распределения.

Интервал прогнозирования для любой стандартной оценки z численно соответствует (1− (1 − Φ μ, σ (z)) · 2).

Например, Φ (2) ≈ 0,9772 или Pr (X ≤ μ + 2σ) ≈ 0,9772, что соответствует интервалу прогноза (1 - (1 - 0,97725) · 2) = 0,9545 = 95,45%.. Это не симметричный интервал - это просто вероятность того, что наблюдение меньше μ + 2σ. Чтобы вычислить вероятность того, что наблюдение находится в пределах двух стандартных отклонений от среднего (небольшие различия из-за округления):

$Pr\; (\mu \; -\; 2\; \sigma \; \le \; X\; \le \; \mu \; +\; 2\; \sigma )\; =\; \Phi \; (2)\; -\; \Phi \; (-\; 2)\; \approx \; 0,9772\; -\; (1\; -\; 0,9772)\; \approx \; 0,9545\; \{\backslash \; displaystyle\; \backslash \; Pr\; (\backslash \; mu\; -2\; \backslash \; sigma\; \backslash \; leq\; X\; \backslash \; leq\; \backslash \; mu\; +2\; \backslash \; sigma)\; =\; \backslash \; Phi\; (2)\; -\; \backslash \; Phi\; (-2)\; \backslash \; приблизительно\; 0,9772-\; (1-0,9772)\; \backslash \; приблизительно\; 0,9545\}$

Это связано с доверительным интервалом, используемым в статистике: $X\; ¯\; \pm \; 2\; \sigma \; n\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{X\}\}\; \backslash \; pm\; 2\; \{\backslash \; frac\; \{\backslash \; sigma\}\; \{\backslash \; sqrt\; \{n\}\}\}\}$- это приблизительно 95% доверительный интервал, когда $X\; ¯\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{X\}\}\}$- среднее значение выборки размером $n\; \{\backslash \; displaystyle\; n\}$.

«Правило 68–95–99,7» часто используется для быстрого получения приблизительной оценки. оценка вероятности чего-либо с учетом его стандартного отклонения, если предполагается, что совокупность является нормальной. Он также используется в качестве простого теста для выбросов, если совокупность считается нормальной, и в качестве теста на нормальность, если совокупность потенциально ненормальна.

Чтобы перейти от выборки к ряду стандартных отклонений, сначала вычисляется отклонение, либо ошибка , либо остаток в зависимости от того, известно ли вам среднее значение генеральной совокупности или только оценивает это. Следующим шагом является стандартизация (деление на стандартное отклонение совокупности), если параметры совокупности известны, или студентизация (деление на оценку стандартного отклонения), если параметры неизвестно и только оценено.

Для использования в качестве теста на выбросы или теста на нормальность вычисляется размер отклонений в единицах стандартных отклонений и сравнивается с ожидаемой частотой. Учитывая набор выборок, можно вычислить стьюдентизированные остатки и сравнить их с ожидаемой частотой: точки, которые отклоняются более чем на 3 стандартных отклонения от нормы, скорее всего, являются выбросами (если только размер выборки является значительно большим, поэтому можно ожидать, что выборка будет такой экстремальной), и если имеется много точек, превышающих 3 стандартных отклонения от нормы, вероятно, есть основания усомниться в предполагаемой нормальности распределения. Это еще более верно для ходов с 4 и более стандартными отклонениями.

Можно вычислить более точно, аппроксимируя количество крайних ходов заданной величины или больше с помощью распределения Пуассона, но просто, если у одного есть несколько четырех стандартных отклонений в выборке размера 1000, у каждого есть веские основания рассматривать эти выбросы или подвергать сомнению предполагаемую нормальность распределения.

Например, событие 6σ соответствует вероятности примерно двух частей на миллиард. Например, если считать, что события происходят ежедневно, это будет соответствовать событию, ожидаемому каждые 1,4 миллиона лет. Это дает простой тест на нормальность : если в ежедневных данных наблюдается 6σ и прошло значительно меньше 1 миллиона лет, то нормальное распределение, скорее всего, не дает хорошей модели для величины или частоты больших отклонения в этом отношении.

В Черный лебедь, Нассим Николас Талеб приводит пример моделей риска, согласно которым авария Черного понедельника будет соответствовать 36 -σ событие: возникновение такого события должно немедленно указывать на то, что модель неисправна, т. е. что рассматриваемый процесс не моделируется удовлетворительным образом с помощью нормального распределения. Затем следует рассмотреть уточненные модели, например введением стохастической волатильности. В таких обсуждениях важно осознавать проблему ошибки игрока, которая гласит, что единичное наблюдение редкого события не противоречит тому, что событие действительно редкое. Наблюдение множества предположительно редких событий все больше опровергает гипотезу о том, что они редки, то есть достоверность предполагаемой модели. Правильное моделирование этого процесса постепенной утраты уверенности в гипотезе потребовало бы обозначения априорной вероятности не только для самой гипотезы, но и для всех возможных альтернативных гипотез. По этой причине проверка статистических гипотез работает не столько путем подтверждения гипотезы, считающейся вероятной, сколько путем опровержения гипотез, считающихся маловероятными.

Из-за экспоненциальные хвосты нормального распределения, вероятность более высоких отклонений уменьшается очень быстро. Из правил для нормально распределенных данных для ежедневного события:

Диапазон	Ожидаемая доля населения внутри диапазона	Приблизительная ожидаемая частота вне диапазона				Приблизительная частота ежедневного события
μ ± 0,5σ	0,382924922548026		3 в	5		Четыре или пять раз в неделю
μ ± σ	0,682689492137086		1 из	3		Дважды в неделю
μ ± 1,5σ	0,866385597462284		1 из	7		Еженедельно
μ ± 2σ	0,954499736103642		1 дюйм	22		Каждые три недели
μ ± 2,5σ	0,987580669348448		1 из	81		Ежеквартально
μ ± 3σ	0,997300203936740		1 дюйм	370		Ежегодно
μ ± 3,5σ	0,999534741841929		1 дюйм	2149		Каждые 6 лет
μ ± 4σ	0,999936657516334		1 из	15787		Каждые 43 года (дважды за всю жизнь)
μ ± 4.5σ	0,999993204653751		1 из	147160		Каждые 403 года (один раз в современную эпоху)
μ ± 5σ	0,9999 99426696856		1 из	1744278		Каждые 4776 лет (один раз в зарегистрированной истории)
μ ± 5,5σ	0,999999962020875		1 из	26330254		Каждые 72090 лет (трижды в истории современного человечества )
μ ± 6σ	0,999999998026825		1 из	506797346		Каждые 1,38 миллиона лет ( дважды в истории человечества )
μ ± 6.5σ	0.999999999919680		1 из	12450197393		Каждые 34 миллиона лет (дважды с момента исчезновения динозавры )
μ ± 7σ	0,999999999997440		1 в	390682215445		Каждые 1,07 миллиарда лет (четыре появления в истории Земли )
μ ± xσ	$erf\; \; (x\; 2)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{erf\}\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{\backslash \; sqrt\; \{2\}\}\}\; \backslash \; right)\}$		1 из	$1\; 1\; -\; erf\; \; (\; x\; 2)\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{1\}\; \{1-\; \backslash \; operatorname\; \{erf\}\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{\backslash \; sqrt\; \{2\}\}\}\; \backslash \; right)\}\}\}$		Каждые $1\; 1\; -\; erf\; \; (x\; 2)\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{1\}\; \{1-\; \backslash \; operatorname\; \{erf\}\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{\backslash \; sqrt\; \{2\}\}\}\; \backslash \; right)\}\}\}$дней

• p-значение
• Six Sigma # Sigma levels
• Стандартный балл
• t-статистика

• "Нормальное распределение » Баласубраманиан Нарасимхан
• "Вычислить процентную долю в пределах x сигм в WolframAlpha