Альфапедия

Вписанный угол

редактировать
Вписанный угол θ составляет половину центрального угла 2θ, который образует ту же дугу на окружности. Таким образом, угол θ не изменяется при перемещении его вершины по окружности.

В geometry вписанный угол - это угол, образованный в внутренность окружности, когда две секущие линии пересекаются на окружности. Его также можно определить как угол, соединенный в одной точке окружности двумя заданными точками на окружности.

Эквивалентно вписанный угол определяется двумя хордами окружности, имеющими общую конечную точку.

Теорема о вписанном угле связывает размер вписанного угла с размером центрального угла, образующего ту же самую дугу.

Теорема о вписанном угле появляется как Предложение 20 в книге 3 «Элементов» Евклида.

Содержание
  • 1 Теорема
    • 1.1 Утверждение
    • 1.2 Доказательство
      • 1.2.1 Вписанные углы, где одна хорда является диаметром
      • 1.2.2 Вписанные углы с центром круга внутри их
      • 1.2.3 Вписанные углы с центром круга снаружи
    • 1.3 Следствие
  • 2 Приложения
  • 3 Теоремы о вписанных углах для эллипсов, гипербол и парабол
  • 4 Ссылки
  • 5 Внешние ссылки
Теорема

Утверждение

Для фиксированных точек A и B, множество точек M на плоскости для которой угол AMB равен α, является дугой окружности. Мера AOB, где O - центр круга, равна 2α.

Теорема о вписанном угле утверждает, что угол θ, вписанный в круг, составляет половину центрального угла 2θ, который соединяет такая же дуга на окружности. Следовательно, угол не меняется, поскольку его вершина перемещается в разные позиции на окружности.

Доказательство

Вписанные углы, где одна хорда - это диаметр

Случай: Одна хорда - это диаметр

Пусть O будет центром круга, как на диаграмме справа. Выберите две точки на окружности и назовите их V и A. Проведите линию VO и пройдите за O так, чтобы она пересекала окружность в точке B, которая диаметрально противоположна точке V. Нарисуйте угол, вершина - это точка V, стороны которой проходят через точки A и B.

Проведите линию OA. Угол BOA - это центральный угол ; назовем это θ. Обе линии OV и OA являются радиусами окружности, поэтому имеют одинаковую длину. Следовательно, треугольник VOA равен равнобедренный, поэтому угол BVA (вписанный угол) и угол VAO равны; обозначим каждый из них ψ.

Углы BOA и AOV являются дополнительными. В сумме они составляют 180 °, поскольку линия VB, проходящая через точку O, является прямой линией. Следовательно, угол AOV составляет 180 ° - θ.

Известно, что три угла треугольника в сумме составляют 180 °, а три угла треугольника VOA равны:

180 ° - θ
ψ
ψ.

Следовательно,

2 ψ + 180 ∘ - θ = 180 ∘. {\ displaystyle 2 \ psi +180 ^ {\ circ} - \ theta = 180 ^ {\ circ}.}2 \ psi +180 ^ {\ circ} - \ theta = 180 ^ {\ circ}.

Вычтем 180 ° с обеих сторон,

2 ψ = θ, {\ displaystyle 2 \ psi = \ theta,}{\ displaystyle 2 \ psi = \ theta,}

где θ - центральный угол, соединяющий дугу AB, а ψ - вписанный угол, соединяющий дугу AB.

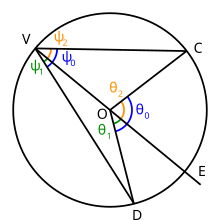Вписанные углы с центром круга внутри их

Случай: центр внутри угла

Для круга, центр которого находится в точке O, выберите три точки V, C и D на окружности. Нарисуйте линии VC и VD: угол DVC - это вписанный угол. Теперь нарисуйте линию VO и протяните ее за точку O так, чтобы она пересекала окружность в точке E. Угол DVC образует дугу DC на окружности.

Предположим, эта дуга включает в себя точку E. Точка E диаметрально противоположна точке V. Углы DVE и EVC также являются вписанными углами, но оба этих угла имеют одну сторону, которая проходит через центр окружности, поэтому к ним может быть применена теорема из части 1 выше.

Следовательно,

∠ D V C = ∠ D V E + ∠ E V C. {\ displaystyle \ angle DVC = \ angle DVE + \ angle EVC.}{\ displaystyle \ angle DVC = \ angle DVE + \ angle EVC.}

, тогда пусть

ψ 0 = ∠ DVC, {\ displaystyle \ psi _ {0} = \ angle DVC,}\ psi _ {0} = \ angle DVC,
ψ 1 = ∠ DVE, {\ displaystyle \ psi _ {1} = \ angle DVE,}\ psi _ {1} = \ angle DVE,
ψ 2 = ∠ EVC, {\ displaystyle \ psi _ {2} = \ angle EVC,}\ psi _ {2} = \ angle EVC,

так, чтобы

ψ 0 = ψ 1 + ψ 2. (1) {\ displaystyle \ psi _ {0} = \ psi _ {1} + \ psi _ {2}. \ Qquad \ qquad (1)}\ psi _ {0} = \ psi _ {1} + \ psi _ {2}. \ qquad \ qquad (1)

Нарисуйте линии OC и OD. Угол DOC является центральным углом, как и углы DOE и EOC, и

∠ D O C = ∠ D O E + ∠ E O C. {\ displaystyle \ angle DOC = \ angle DOE + \ angle EOC.}\ angle DOC = \ angle DOE + \ angle EOC.

Пусть

θ 0 = ∠ DOC, {\ displaystyle \ theta _ {0} = \ angle DOC,}\ theta _ {0} = \ angle DOC,
θ 1 = ∠ ДОЭ, {\ displaystyle \ theta _ {1} = \ angle DOE,}\ theta _ {1} = \ angle DOE,
θ 2 = ∠ EOC, {\ displaystyle \ theta _ {2} = \ angle EOC,}\ theta _ {2} = \ angle EOC,

так, чтобы

θ 0 = θ 1 + θ 2. (2) {\ displaystyle \ theta _ {0} = \ theta _ {1} + \ theta _ {2}. \ Qquad \ qquad (2)}\ theta _ {0} = \ theta _ {1} + \ theta _ {2}. \ Qquad \ qquad (2)

Из первой части мы знаем, что θ 1 = 2 ψ 1 {\ displaystyle \ theta _ {1} = 2 \ psi _ {1}}\ theta _ {1} = 2 \ psi _ {1} и что θ 2 = 2 ψ 2 {\ displaystyle \ theta _ {2} = 2 \ psi _ {2}}\ theta _ {2} = 2 \ psi _ {2 } . Объединение этих результатов с уравнением (2) дает

θ 0 = 2 ψ 1 + 2 ψ 2 {\ displaystyle \ theta _ {0} = 2 \ psi _ {1} +2 \ psi _ {2}}{\ displaystyle \ theta _ {0} = 2 \ psi _ {1} +2 \ psi _ {2}}

следовательно, по уравнению (1)

θ 0 = 2 ψ 0. {\ displaystyle \ theta _ {0} = 2 \ psi _ {0}.}\ theta _ {0} = 2 \ psi _ {0}.

Вписанные углы с центром круга снаружи

Случай: центр снаружи от угла

Предыдущий случай может быть расширен, чтобы охватить случай, когда мерой вписанного угла является разница между двумя вписанными углами, как обсуждалось в первой части этого доказательства.

Для окружности с центром в точке O выберите три точки V, C и D на окружности. Нарисуйте линии VC и VD: угол DVC - это вписанный угол. Теперь нарисуйте линию VO и протяните ее за точку O так, чтобы она пересекала окружность в точке E. Угол DVC образует дугу DC на окружности.

Предположим, эта дуга не включает в себя точку E. Точка E диаметрально противоположна точке V. Углы EVD и EVC также являются вписанными углами, но оба этих угла имеют одну сторону, которая проходит через центр окружности, поэтому к ним может быть применена теорема из части 1 выше.

Следовательно,

∠ DVC = ∠ EVC - ∠ EVD {\ displaystyle \ angle DVC = \ angle EVC- \ angle EVD}{\ displaystyle \ angle DVC = \ angle EVC- \ angle EVD} .

, тогда пусть

ψ 0 = ∠ DVC, {\ displaystyle \ psi _ {0} = \ angle DVC,}\ psi _ {0} = \ angle DVC,
ψ 1 = ∠ EVD, {\ displaystyle \ psi _ {1} = \ angle EVD,}{\ displaystyle \ psi _ {1} = \ angle EVD,}
ψ 2 = ∠ EVC, {\ displaystyle \ psi _ {2} = \ angle EVC,}\ psi _ {2} = \ angle EVC,

, так что

ψ 0 = ψ 2 - ψ 1. (3) {\ displaystyle \ psi _ {0} = \ psi _ {2} - \ psi _ {1}. \ Qquad \ qquad (3)}\ psi _ {0} = \ psi _ {2} - \ psi _ {1}. \ Qquad \ qquad (3)

Нарисуйте линии OC и OD. Угол DOC является центральным углом, как и углы EOD и EOC, и

∠ D O C = ∠ E O C - ∠ E O D. {\ displaystyle \ angle DOC = \ angle EOC- \ angle EOD.}{\ displaystyle \ angle DOC = \ angle EOC- \ angle EOD.}

Пусть

θ 0 = ∠ DOC, {\ displaystyle \ theta _ {0} = \ angle DOC,}\ theta _ {0} = \ angle DOC,
θ 1 = ∠ EOD, {\ displaystyle \ theta _ {1} = \ angle EOD,}{\ displaystyle \ theta _ {1} = \ angle EOD,}
θ 2 = ∠ EOC, {\ displaystyle \ theta _ {2} = \ angle EOC,}\ theta _ {2} = \ angle EOC,

так, чтобы

θ 0 = θ 2 - θ 1. (4) {\ displaystyle \ theta _ {0} = \ theta _ {2} - \ theta _ {1}. \ Qquad \ qquad (4)}\ theta _ { 0} = \ theta _ {2} - \ theta _ {1}. \ Qquad \ qquad (4)

Из первой части мы знаем, что θ 1 = 2 ψ 1 {\ displaystyle \ theta _ {1} = 2 \ psi _ {1}}\ theta _ {1} = 2 \ psi _ {1} и что θ 2 = 2 ψ 2 {\ displaystyle \ theta _ {2} = 2 \ psi _ {2}}\ theta _ {2} = 2 \ psi _ {2 } . Объединение этих результатов с уравнением (4) дает

θ 0 = 2 ψ 2 - 2 ψ 1 {\ displaystyle \ theta _ {0} = 2 \ psi _ {2} -2 \ psi _ {1}}\ theta _ {0} = 2 \ psi _ {2} -2 \ psi _ {1}

следовательно, по уравнению (3)

θ 0 = 2 ψ 0. {\ displaystyle \ theta _ {0} = 2 \ psi _ {0}.}\ theta _ {0} = 2 \ psi _ {0}.

Следствие

По аналогичному аргументу угол между хордой и касательная линия в одной из точек ее пересечения равна половине центрального угла, образуемого хордой. См. Также Касательные прямые к окружностям.

Приложения

Теорема о вписанном угле используется во многих доказательствах элементарной евклидовой геометрии плоскости. Частным случаем теоремы является теорема Фалеса, в которой говорится, что угол, образуемый диаметром , всегда равен 90 °, то есть прямому углу. Как следствие теоремы, сумма противоположных углов циклических четырехугольников равна 180 °; И наоборот, любой четырехугольник, для которого это верно, можно вписать в круг. В качестве другого примера, теорема о вписанном угле является основой для нескольких теорем, связанных со степенью точки по отношению к окружности. Кроме того, это позволяет доказать, что, когда две хорды пересекаются по окружности, произведения длин их частей равны.

Вписанные угловые теоремы для эллипсов, гипербол и парабол

Вписанные угловые теоремы существуют также для эллипсов, гипербол и парабол. Существенные отличия - это размеры угла. (Угол рассматривается как пара пересекающихся линий.)

Ссылки
  • Огилви, С.С. (1990). Экскурсии по геометрии. Дувр. С. 17–23. ISBN 0-486-26530-7.
  • Геллерт В., Кюстнер Х., Хеллвич М., Кестнер Х. (1977). Краткая энциклопедия математики VNR. Нью-Йорк: Ван Ностранд Рейнхольд. п. 172. ISBN 0-442-22646-2.
  • Моис, Эдвин Э. (1974). Элементарная геометрия с продвинутой точки зрения (2-е изд.). Читает: Эддисон-Уэсли. С. 192–197. ISBN 0-201-04793-4.
Внешние ссылки
Последняя правка сделана 2021-05-24 03:18:29
Содержание доступно по лицензии CC BY-SA 3.0 (если не указано иное).
Обратная связь: support@alphapedia.ru
Соглашение
О проекте