Твердое тело Эйнштейна

Твердое тело Эйнштейна - это модель твердого тела, основанная на двух предположениях:

• Каждый атом в решетка представляет собой независимый трехмерный квантовый гармонический осциллятор
• Все атомы колеблются с одинаковой частотой (в отличие от модели Дебая )

Хотя предположение о том, что твердое тело имеет независимые колебания, является очень точным, эти колебания являются здравыми волны или фононы, коллективные моды, включающие множество атомов. Однако в модели Эйнштейна каждый атом колеблется независимо. Эйнштейн знал, что получить частоту реальных колебаний будет сложно, но тем не менее он предложил эту теорию, потому что это была особенно ясная демонстрация того, что квантовая механика может решить проблему удельной теплоты в классической механике.

• 1 Историческое влияние
• 2 Выведение теплоемкости
  • 2.1. микроканонический ансамбль
  • 2.2 В каноническом ансамбле
• 3 Limitati модели и последующие модели
• 4 См. также
• 5 Ссылки
• 6 Внешние ссылки

Первоначальная теория, предложенная Эйнштейном в 1907 году, имеет большое историческое значение. теплоемкость твердых тел, предсказанная эмпирическим законом Дюлонга – Пети, требовалась классической механикой, удельная теплоемкость твердых тел должна не зависеть от температуры. Но эксперименты при низких температурах показали, что теплоемкость меняется, стремясь к нулю при абсолютном нуле. По мере повышения температуры удельная теплоемкость увеличивается до тех пор, пока не приближается к прогнозам Дюлонга и Пети при высокой температуре.

Используя предположение Планка квантования, теория Эйнштейна впервые учла наблюдаемую экспериментальную тенденцию. Вместе с фотоэлектрическим эффектом это стало одним из наиболее важных доказательств необходимости квантования. Эйнштейн использовал уровни квантово-механического осциллятора за много лет до появления современной квантовой механики.

Для термодинамического подхода теплоемкость может быть получена с использованием различных статистические ансамбли. Все решения эквивалентны при термодинамическом пределе .

В микроканоническом ансамбле

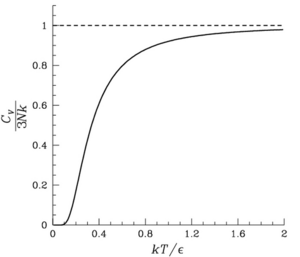
Теплоемкость твердого тела Эйнштейна как функция температуры. Экспериментальное значение 3Nk восстанавливается при высоких температурах.

Теплоемкость объекта при постоянном объеме V определяется через внутреннюю энергию U как

$CV\; =\; (\partial \; U\; \partial \; T)\; V.\; \{\backslash \; displaystyle\; C\_\; \{V\}\; =\; \backslash \; left\; (\{\backslash \; partial\; U\; \backslash \; over\; \backslash \; partial\; T\}\; \backslash \; right)\; \_\; \{V\}.\}$

$T\; \{\backslash \; displaystyle\; T\}$, температура системы, можно найти из энтропии

$1\; T\; =\; \partial \; S\; \partial \; U.\; \{\backslash \; displaystyle\; \{1\; \backslash \; over\; T\}\; =\; \{\backslash \; partial\; S\; \backslash \; over\; \backslash \; partial\; U\}.\}$

Чтобы найти энтропию, рассмотрим твердое тело, состоящее из $N\; \{\backslash \; displaystyle\; N\}$атомов, каждая из которых имеет 3 степени свободы. Итак, существует $3\; N\; \{\backslash \; displaystyle\; 3N\}$квантовых гармонических осцилляторов (далее SHO для «простых гармонических осцилляторов»).

$N\; \prime \; =\; 3\; N\; \{\backslash \; displaystyle\; N\; ^\; \{\backslash \; prime\}\; =\; 3N\}$

Возможные энергии SHO даются как

$E\; n\; =\; \hslash \; \omega \; (n\; +\; 1\; 2)\; \{\backslash \; displaystyle\; E\_\; \{\; n\}\; =\; \backslash \; hbar\; \backslash \; omega\; \backslash \; left\; (n\; +\; \{1\; \backslash \; over\; 2\}\; \backslash \; right)\}$

или, другими словами, уровни энергии распределены равномерно, и можно определить квант энергии

$\epsilon \; =\; \hslash \; \omega \; \{\backslash \; displaystyle\; \backslash \; varepsilon\; =\; \backslash \; hbar\; \backslash \; omega\}$

, которая является наименьшей и единственной величиной, на которую увеличивается энергия SHO. Затем мы должны вычислить кратность системы. То есть вычислить количество способов распределить $q\; \{\backslash \; displaystyle\; q\}$кванты энергии между $N\; \prime \; \{\backslash \; displaystyle\; N\; ^\; \{\backslash \; prime\}\}$SHOs. Эта задача становится проще, если подумать о распределении $q\; \{\backslash \; displaystyle\; q\}$гальки по $N\; \prime \; \{\backslash \; displaystyle\; N\; ^\; \{\backslash \; prime\}\}$коробок

или разделение стопок гальки с помощью $N\; \prime \; -\; 1\; \{\backslash \; displaystyle\; N\; ^\; \{\backslash \; prime\}\; -1\}$перегородок

или расположение $q\; \{\backslash \; displaystyle\; q\}$камешки и $N\; \prime \; -\; 1\; \{\backslash \; displaystyle\; N\; ^\; \{\backslash \; prime\}\; -1\}$перегородки

Последнее изображение наиболее показательно. Количество расположений объектов $n\; \{\backslash \; displaystyle\; n\}$равно $n!\; \{\backslash \; displaystyle\; n!\}$. Таким образом, количество возможных расположений $q\; \{\backslash \; displaystyle\; q\}$гальки и $N\; \prime \; -\; 1\; \{\backslash \; displaystyle\; N\; ^\; \{\backslash \; prime\}\; -1\}$разделов равно $(q\; +\; N\; \prime \; -\; 1)!\; \{\backslash \; displaystyle\; \backslash \; left\; (q\; +\; N\; ^\; \{\backslash \; prime\}\; -1\; \backslash \; right)!\}$. Но если поменяться местами раздел №3 и раздел №5, никто не заметит. То же самое касается квантов. Чтобы получить количество возможных различимых расположений, нужно разделить общее количество расположений на количество неразличимых расположений. Есть $q!\; \{\backslash \; displaystyle\; q!\}$идентичное расположение квантов и $(N\; \prime \; -\; 1)!\; \{\backslash \; displaystyle\; (N\; ^\; \{\backslash \; prime\}\; -1)!\}$идентичное расположение разделов. Следовательно, кратность системы равна

$\Omega \; =\; (q\; +\; N\; \prime \; -\; 1)!\; д!\; (N\; \prime \; -\; 1)!\; \{\backslash \; displaystyle\; \backslash \; Omega\; =\; \{\backslash \; left\; (q\; +\; N\; ^\; \{\backslash \; prime\}\; -1\; \backslash \; right)!\; \backslash \; over\; q!\; (N\; ^\; \{\backslash \; prime\}\; -1)!\}\}$

который, как упоминалось ранее, является количеством способов внесения $q\; \{\backslash \; displaystyle\; q\}$квантов энергии в осцилляторы $N\; \prime \; \{\backslash \; displaystyle\; N\; ^\; \{\backslash \; prime\}\}$. Энтропия системы имеет вид

$S\; /\; k\; =\; ln\; \; \Omega \; =\; ln\; \; (q\; +\; N\; \prime \; -\; 1)!\; д!\; (N\; \prime \; -\; 1)!.\; \{\backslash \; Displaystyle\; S\; /\; к\; =\; \backslash \; ln\; \backslash \; Omega\; =\; \backslash \; ln\; \{\backslash \; left\; (q\; +\; N\; ^\; \{\backslash \; prime\}\; -1\; \backslash \; right)!\; \backslash \; over\; q!\; (N\; ^\; \{\backslash \; prime\}\; -1)!\}.\}$

$N\; \prime \; \{\backslash \; displaystyle\; N\; ^\; \{\backslash \; prime\}\}$- огромное число - вычитание из него единицы не имеет общий эффект вообще:

$S\; /\; k\; \approx \; ln\; \; (q\; +\; N\; \prime )!\; д!\; Н\; \text{'}!\; \{\backslash \; Displaystyle\; S\; /\; к\; \backslash \; приблизительно\; \backslash \; ln\; \{\backslash \; left\; (q\; +\; N\; ^\; \{\backslash \; prime\}\; \backslash \; right)!\; \backslash \; over\; q!\; N\; ^\; \{\backslash \; prime\}!\}\}$

С помощью приближения Стирлинга энтропию можно упростить:

$S\; /\; k\; \approx \; (q\; +\; N\; \prime )\; ln\; \; (\; q\; +\; N\; \prime )\; -\; N\; \prime \; ln\; \; N\; \prime \; -\; q\; ln\; \; q.\; \{\backslash \; Displaystyle\; S\; /\; к\; \backslash \; приблизительно\; \backslash \; влево\; (д\; +\; N\; ^\; \{\backslash \; prime\}\; \backslash \; right)\; \backslash \; ln\; \backslash \; left\; (q\; +\; N\; ^\; \{\backslash \; prime\}\; \backslash \; right)\; -N\; ^\; \{\backslash \; prime\}\; \backslash \; ln\; N\; ^\; \{\; \backslash \; prime\}\; -q\; \backslash \; ln\; q.\}$

Полная энергия твердого тела определяется как

$U\; =\; N\; \prime \; \epsilon \; 2\; +\; q\; \epsilon ,\; \{\backslash \; displaystyle\; U\; =\; \{N\; ^\; \{\backslash \; prime\}\; \backslash \; varepsilon\; \backslash \; over\; 2\}\; +\; q\; \backslash \; varepsilon,\}$

, поскольку всего в системе есть q квантов энергии в дополнение к энергии основного состояния каждого осциллятора. Некоторые авторы, такие как Шредер, опускают эту энергию основного состояния в своем определении полной энергии твердого тела Эйнштейна.

Теперь мы готовы вычислить температуру

$1\; T\; =\; \partial \; S\; \partial \; U\; =\; \partial \; S\; \partial \; qdqd\; U\; =\; 1\; \epsilon \; \partial \; S\; \partial \; q\; =\; k\; \epsilon \; ln\; \; (1\; +\; N\; \prime \; /\; q)\; \{\backslash \; Displaystyle\; \{1\; \backslash \; над\; T\}\; =\; \{\backslash \; partial\; S\; \backslash \; over\; \backslash \; partial\; U\}\; =\; \{\backslash \; partial\; S\; \backslash \; over\; \backslash \; partial\; q\}\; \{dq\; \backslash \; over\; dU\}\; =\; \{1\; \backslash \; over\; \backslash \; varepsilon\}\; \{\backslash \; partial\; S\; \backslash \; over\; \backslash \; partial\; q\}\; =\; \{k\; \backslash \; over\; \backslash \; varepsilon\}\; \backslash \; ln\; \backslash \; left\; (1\; +\; N\; ^\; \{\backslash \; prime\}\; /\; q\; \backslash \; right)\}$

Исключение q между двумя предыдущими формулами дает для U:

$U\; =\; N\; \prime \; \epsilon \; 2\; +\; N\; \prime \; \epsilon \; e\; \epsilon \; /\; k\; T\; -\; 1.\; \{\backslash \; displaystyle\; U\; =\; \{N\; ^\; \{\backslash \; prime\}\; \backslash \; varepsilon\; \backslash \; over\; 2\}\; +\; \{N\; ^\; \{\backslash \; prime\}\; \backslash \; varepsilon\; \backslash \; over\; e\; ^\; \{\backslash \; varepsilon\; /\; kT\}\; -1\}.\}$

Первый член связан с нулевой энергией и не влияет на удельную теплоемкость. Поэтому на следующем шаге он будет потерян.

Дифференцируя по температуре, чтобы найти $CV\; \{\backslash \; displaystyle\; C\_\; \{V\}\}$, получаем:

$CV\; =\; \partial \; U\; \partial \; T\; =\; N\; \prime \; \epsilon \; 2\; k\; T\; 2\; е\; \epsilon \; /\; К\; T\; (е\; \epsilon \; /\; К\; T\; -\; 1)\; 2\; \{\backslash \; Displaystyle\; C\_\; \{V\}\; =\; \{\backslash \; partial\; U\; \backslash \; over\; \backslash \; partial\; T\}\; =\; \{N\; ^\; \{\backslash \; prime\}\; \backslash \; varepsilon\; ^\; \{2\}\; \backslash \; over\; kT\; ^\; \{2\}\}\; \{e\; ^\; \{\backslash \; varepsilon\; /\; kT\}\; \backslash \; over\; \backslash \; left\; (e\; ^\; \{\backslash \; varepsilon\; /\; kT\}\; -1\; \backslash \; right)\; ^\; \{2\}\}\}$

или

$CV\; =\; 3\; N\; К\; (е\; К\; Т)\; 2\; е\; е\; /\; к\; Т\; (е\; е\; /\; к\; Т\; -\; 1)\; 2.\; \{\backslash \; Displaystyle\; C\_\; \{V\}\; =\; 3Nk\; \backslash \; left\; (\{\backslash \; varepsilon\; \backslash \; over\; kT\}\; \backslash \; right)\; ^\; \{2\}\; \{e\; ^\; \{\backslash \; varepsilon\; /\; kT\}\; \backslash \; over\; \backslash \; left\; (e\; ^\; \{\backslash \; varepsilon\; /\; kT\}\; -1\; \backslash \; right)\; ^\; \{2\}\}.\}$

Хотя модель твердого тела Эйнштейна точно предсказывает теплоемкость при высоких температурах, и в этом пределе

$lim\; T\; \to \; \infty \; CV\; =\; 3\; N\; k\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{T\; \backslash \; rightarrow\; \backslash \; infty\}\; C\_\; \{V\}\; =\; 3Nk\}$,

что эквивалентно закону Дюлонга – Пти.

Тем не менее, теплоемкость заметно отклоняется от экспериментальных значений при низких температурах. См. модель Дебая, чтобы узнать, как точно рассчитать низкотемпературную теплоемкость.

В каноническом ансамбле

Теплоемкость получается за счет использования канонической статистической суммы простого квантового гармонического осциллятора.

$Z\; знак\; равно\; \sum \; N\; =\; 0\; \infty \; е\; -\; E\; N\; /\; К\; T\; \{\backslash \; Displaystyle\; Z\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; E\_\; \{n\}\; /\; kT\}\}$

где

$E\; n\; =\; \epsilon \; (n\; +\; 1\; 2)\; \{\backslash \; displaystyle\; E\_\; \{n\}\; =\; \backslash \; varepsilon\; \backslash \; left\; (n\; +\; \{1\; \backslash \; over\; 2\}\; \backslash \; right)\}$

, подставив это в формулу статистической суммы, получаем

$Z\; =\; \sum \; n\; =\; 0\; \infty \; e\; -\; \epsilon \; (n\; +\; 1/2)\; /\; k\; T\; =\; e\; -\; \epsilon \; /\; 2\; k\; T\; \sum \; n\; =\; 0\; \infty \; e\; -\; n\; \epsilon \; /\; k\; T\; =\; e\; -\; \epsilon \; /\; 2\; k\; T\; \sum \; n\; =\; 0\; \infty \; (e\; -\; \epsilon \; /\; k\; T)\; n\; =\; e\; -\; \epsilon \; /\; 2\; k\; T\; 1\; -\; e\; -\; \epsilon \; /\; k\; T\; =\; 1\; e\; \epsilon \; /\; 2\; k\; T\; -\; e\; -\; \epsilon \; /\; 2\; k\; T\; =\; 1\; 2\; sinh\; \; (\epsilon \; 2\; k\; T).\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; Z\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; \backslash \; varepsilon\; \backslash \; left\; (n\; +\; 1/2\; \backslash \; right)\; /\; kT\}\; =\; e\; ^\; \{-\; \backslash \; varepsilon\; /\; 2kT\}\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; n\; \backslash \; varepsilon\; /\; kT\}\; =\; e\; ^\; \{-\; \backslash \; varepsilon\; /\; 2kT\}\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (e\; ^\; \{-\; \backslash \; varepsilon\; /\; kT\}\; \backslash \; right)\; ^\; \{n\}\; \backslash \backslash \; =\; \{e\; ^\; \{-\; \backslash \; varepsilon\; /\; 2kT\}\; \backslash \; over\; 1-e\; ^\; \{-\; \backslash \; varepsilon\; /\; kT\}\}\; =\; \{1\; \backslash \; над\; e\; ^\; \{\backslash \; varepsilon\; /\; 2kT\}\; -e\; ^\; \{-\; \backslash \; varepsilon\; /\; 2kT\}\}\; =\; \{1\; \backslash \; over\; 2\; \backslash \; sinh\; \backslash \; left\; (\{\backslash \; varepsilon\; \backslash \; over\; 2kT\}\; \backslash \; right)\}.\; \backslash \; end\; \{align\}\}\}$

Это статистическая сумма одного гармонического осциллятора. Поскольку статистически теплоемкость, энергия и энтропия твердого тела равномерно распределены между его атомами, мы можем работать с этой статистической суммой, чтобы получить эти величины, а затем просто умножить их на $N\; \prime \; \{\backslash \; displaystyle\; N\; ^\; \{\backslash \; prime\}\}$, чтобы получить итог. Затем давайте вычислим среднюю энергию каждого осциллятора

$⟨E⟩\; =\; U\; =\; -\; 1\; Z\; \partial \; \beta \; Z\; \{\backslash \; displaystyle\; \backslash \; langle\; E\; \backslash \; rangle\; =\; U\; =\; -\; \{1\; \backslash \; over\; Z\}\; \backslash \; partial\; \_\; \{\backslash \; beta\}\; Z\}$

где

$\beta \; =\; 1\; k\; T.\; \{\backslash \; displaystyle\; \backslash \; beta\; =\; \{1\; \backslash \; over\; kT\}.\}$

Следовательно,

$U\; =\; -\; 2\; sinh\; \; (\epsilon \; 2\; k\; T)\; -\; cosh\; \; (\epsilon \; 2\; k\; T)\; 2\; sinh\; 2\; \; (\epsilon \; 2\; k\; T)\; \epsilon \; 2\; =\; \epsilon \; 2\; coth\; \; (\epsilon \; 2\; k\; T).\; \{\backslash \; Displaystyle\; U\; =\; -2\; \backslash \; sinh\; \backslash \; left\; (\{\backslash \; varepsilon\; \backslash \; over\; 2kT\}\; \backslash \; right)\; \{-\; \backslash \; cosh\; \backslash \; left\; (\{\backslash \; varepsilon\; \backslash \; over\; 2kT\}\; \backslash \; right)\; \backslash \; over\; 2\; \backslash \; sinh\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; varepsilon\; \backslash \; over\; 2kT\}\; \backslash \; right)\}\; \{\backslash \; varepsilon\; \backslash \; over\; 2\}\; =\; \{\backslash \; varepsilon\; \backslash \; over\; 2\}\; \backslash \; coth\; \backslash \; left\; (\{\backslash \; varepsilon\; \backslash \; over\; 2kT\}\; \backslash \; right).\}$

Теплоемкость тогда один осциллятор

$c\; V\; =\; \partial \; U\; \partial \; T\; =\; -\; \epsilon \; 2\; 1\; sinh\; 2\; \; (\epsilon \; 2\; k\; T)\; (-\; \epsilon \; 2\; k\; T\; 2)\; =\; k\; (\epsilon \; 2\; k\; T)\; 2\; 1\; sinh\; 2\; \; (\; \epsilon \; 2\; к\; Тл).\; \{\backslash \; Displaystyle\; c\_\; \{V\}\; =\; \{\backslash \; partial\; U\; \backslash \; over\; \backslash \; partial\; T\}\; =\; -\; \{\backslash \; varepsilon\; \backslash \; over\; 2\}\; \{1\; \backslash \; over\; \backslash \; sinh\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; varepsilon\; \backslash \; over\; 2kT\}\; \backslash \; right)\; \}\; \backslash \; left\; (-\; \{\backslash \; varepsilon\; \backslash \; over\; 2kT\; ^\; \{2\}\}\; \backslash \; right)\; =\; k\; \backslash \; left\; (\{\backslash \; varepsilon\; \backslash \; over\; 2kT\}\; \backslash \; right)\; ^\; \{2\}\; \{1\; \backslash \; over\; \backslash \; sinh\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; varepsilon\; \backslash \; over\; 2kT\}\; \backslash \; right)\}.\}$

До сих пор мы вычисляли теплоемкость единственной степени свободы, которая моделировалась как квантовая гармоника. Теплоемкость всего твердого тела тогда определяется как $CV\; =\; 3\; N\; c\; V\; \{\backslash \; displaystyle\; C\_\; \{V\}\; =\; 3Nc\_\; \{V\}\}$, где общее количество степеней свободы solid - это три (для трех направлений степени свободы), умноженное на $N\; \{\backslash \; displaystyle\; N\}$, количество атомов в твердом теле. Таким образом, получаем

$C\; V\; =\; 3\; N\; k\; (\epsilon \; 2\; k\; T)\; 2\; 1\; sinh\; 2\; \; (\epsilon \; 2\; k\; T).\; \{\backslash \; Displaystyle\; C\_\; \{V\}\; =\; 3Nk\; \backslash \; left\; (\{\backslash \; varepsilon\; \backslash \; over\; 2kT\}\; \backslash \; right)\; ^\; \{2\}\; \{1\; \backslash \; over\; \backslash \; sinh\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; varepsilon\; \backslash \; over\; 2kT\}\; \backslash \; right)\}.\}$

, которая алгебраически идентична формуле, полученной в предыдущем разделе.

Величина $TE\; =\; \epsilon \; /\; k\; \{\backslash \; displaystyle\; T\; \_\; \{\backslash \; rm\; \{E\}\}\; =\; \backslash \; varepsilon\; /\; k\}$имеет размерности температуры и является характерным свойством кристалл. Она известна как температура Эйнштейна . Следовательно, модель кристалла Эйнштейна предсказывает, что энергия и теплоемкость кристалла являются универсальными функциями безразмерного отношения $T\; /\; T\; E\; \{\backslash \; displaystyle\; T\; /\; T\; \_\; \{\backslash \; rm\; \{E\}\}\}$. Точно так же модель Дебая предсказывает универсальную функцию отношения $T\; /\; TD\; \{\backslash \; displaystyle\; T\; /\; T\; \_\; \{\backslash \; rm\; \{D\}\}\}$, где $TD\; \{\backslash \; displaystyle\; T\; \_\; \{\backslash \; rm\; \{D\}\}\}$- температура Дебая.

В модели Эйнштейна удельная теплоемкость экспоненциально быстро приближается к нулю при низких температурах. Это потому, что все колебания имеют одну общую частоту. Правильное поведение обнаруживается путем квантования нормальных мод твердого тела таким же образом, как предложил Эйнштейн. Тогда частоты волн не одинаковы, и удельная теплоемкость стремится к нулю по степенному закону $T\; 3\; \{\backslash \; displaystyle\; T\; ^\; \{3\}\}$, что соответствует эксперименту. Эта модификация называется моделью Дебая, которая появилась в 1912 году.

Когда Вальтер Нернст узнал о статье Эйнштейна 1906 года об удельной теплоемкости, он был так взволнован, что путешествовал весь путь от Берлина до Цюриха, чтобы встретиться с ним.

• Кинетическая теория твердых тел

• Зеленый, Энрике. «Демонстрационный проект Вольфрама - Эйнштейн Солид». Проверено 18 марта 2016 г..