Дерево двоичного выражения

двоичное дерево, представляющее математическое выражение

A дерево двоичного выражения - это особый вид двоичного дерева используется для представления выражений. Двумя распространенными типами выражений, которые может представлять дерево двоичных выражений, являются алгебраический и логический. Эти деревья могут представлять выражения, содержащие операторы унарный и двоичный.

Каждый узел двоичного дерева и, следовательно, дерева двоичных выражений имеет ноль, один, или двое детей. Эта ограниченная структура упрощает обработку деревьев выражений.

• 1 Обзор
  • 1.1 Обход
    • 1.1.1 Обход инфиксов
    • 1.1.2 Постфиксный обход
    • 1.1.3 Обход префикса
• 2 Построение дерева выражения
  • 2.1 Пример
• 3 Алгебраические выражения
• 4 Логические выражения
• 5 См. Также
• 6 Ссылки

Дерево выражений выражения (a + b) * c + 7

листья дерева двоичного выражения являются операндами, такими как константы или имена переменных, а другие узлы содержат операторы. Эти конкретные деревья оказываются двоичными, потому что все операции являются двоичными, и, хотя это самый простой случай, у узлов может быть более двух дочерних элементов. Также возможно, что у узла будет только один дочерний элемент, как в случае с унарным оператором минус. Дерево выражения T можно оценить, применив оператор в корне к значениям, полученным путем рекурсивного вычисления левого и правого поддеревьев.

Обход

Алгебраическое выражение может быть получено из дерево двоичных выражений путем рекурсивного создания левого выражения в скобках, затем распечатки оператора в корне и, наконец, рекурсивного создания правого выражения в скобках. Эта общая стратегия (слева, узел, справа) известна как обход по порядку. Альтернативная стратегия обхода - рекурсивно распечатать левое поддерево, правое поддерево, а затем оператор. Эта стратегия обхода обычно известна как обход после заказа. Третья стратегия - сначала распечатать оператор, а затем рекурсивно распечатать левое и правое поддеревья, известное как обход предварительного заказа.

Эти три стандартных обхода в глубину представляют собой три разных формата выражений: инфиксный, постфикс и префикс. Инфиксное выражение создается при обходе порядка, постфиксное выражение создается обходом пост-порядка, а префиксное выражение создается обходом предварительного порядка.

Обход инфиксов

Когда инфиксное выражение печатается, открывающая и закрывающая круглые скобки должны быть добавлены в начале и в конце каждого выражения. Поскольку каждое поддерево представляет собой часть выражения, открывающая скобка печатается в его начале, а закрывающая скобка печатается после обработки всех его дочерних элементов.

Псевдокод:

Инфиксный алгоритм алгоритма (дерево) / * Вывести инфиксное выражение для дерева выражения. Pre: tree - указатель на дерево выражений Post: инфиксное выражение было напечатано * / if (дерево не пусто) if (токен дерева является оператором) print (открывающая скобка) end if infix (левое поддерево дерева) print (токен дерева) infix (правое поддерево дерева) if (токен дерева - оператор) print (закрывающая скобка) end if end if end infix

Постфиксный обход

Выражение постфиксного формируется базовым обратный обход любого двоичного дерева. Скобки не требуются.

Псевдокод:

Постфикс алгоритма (дерево) / * Вывести постфиксное выражение для дерева выражений. Pre: tree - указатель на дерево выражений. Post: выражение postfix было напечатано * / if (tree not empty) postfix (tree left subtree) postfix (tree right subtree) print (tree token) end if end postfix

Обход префикса

Псевдокод:

Префикс алгоритма (дерево) / * Распечатать префиксное выражение для дерева выражения. Pre: tree - указатель на дерево выражений Post: префиксное выражение было напечатано * / if (tree not empty) print (tree token) prefix (tree left subtree) prefix (tree right subtree) end if end prefix

Построение дерева происходит путем чтения постфиксного выражения по одному символу за раз. Если символ является операндом, создается одноузловое дерево, и его указатель помещается в стек . Если символ является оператором, указатели на два дерева T1 и T2 извлекаются из стека и формируется новое дерево, корнем которого является оператор, а левый и правый дочерние элементы которого указывают на T2 и T1 соответственно. Затем указатель на это новое дерево помещается в стек.

Пример

Ввод в постфиксной нотации: ab + cde + * * Поскольку первые два символа являются операндами, одноузловой создаются деревья, и указатели на них помещаются в стек. Для удобства стек будет расти слева направо.

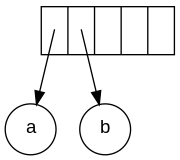Стек растет слева направо

Следующий символ - "+". Он выталкивает два указателя на деревья, формируется новое дерево, и указатель на него помещается в стек.

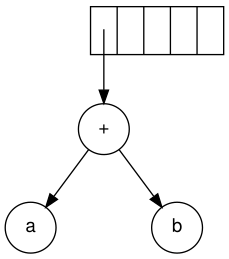Формирование нового дерева

Затем считываются c, d и e. Для каждого создается одноузловое дерево, и указатель на соответствующее дерево помещается в стек.

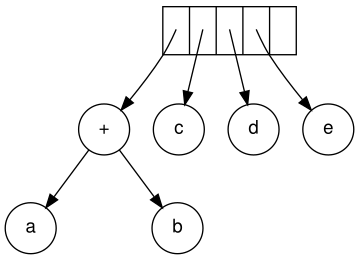Создание дерева с одним узлом

Продолжая, считывается '+', и он объединяет два последних дерева.

Объединение двух деревьев

Теперь читается "*". Выскакивают два последних указателя на дерево, и формируется новое дерево со знаком «*» в качестве корня.

Формирование нового дерева с корнем

Наконец, считывается последний символ. Два дерева объединяются, и указатель на последнее дерево остается в стеке.

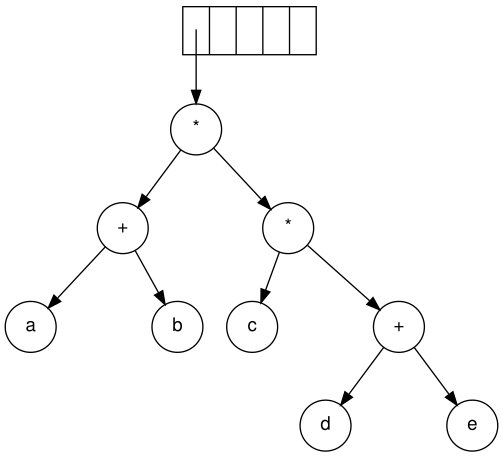Шаги по построению дерева выражений ab + cde + * * Дерево двоичных алгебраических выражений, эквивалентное ((5 + z) / -8) * (4 ^ 2)

Алгебраические деревья выражений представляют собой выражения, содержащие числа, переменные, а также унарные и двоичные операторы. Некоторые из общих операторов: × (умножение ), ÷ (деление ), + (сложение ), - (вычитание ), ^ (возведение в степень ) и - (отрицание ). Операторы содержатся во внутренних узлах дерева, а числа и переменные - в листовых узлах. Узлы бинарных операторов имеют два дочерних узла , а унарные операторы имеют один дочерний узел.

Дерево двоичных логических выражений, эквивалентное ((true $\vee \; \{\backslash \; displaystyle\; \backslash \; lor\}$false) $\wedge \; \{\backslash \; displaystyle\; \backslash \; land\}$$\neg \; \{\; \backslash \; displaystyle\; \backslash \; neg\}$false) $\vee \; \{\backslash \; displaystyle\; \backslash \; lor\}$(true $\vee \; \{\backslash \; displaystyle\; \backslash \; lor\}$false))

Булевы выражения представлены очень похоже на алгебраические выражения, с той лишь разницей, что используются конкретные значения и операторы. Булевы выражения используют истину и ложь в качестве постоянных значений, а операторы включают $\wedge \; \{\backslash \; displaystyle\; \backslash \; land\}$(AND ), $\vee \; \{\backslash \; displaystyle\; \backslash \; lor\}$(OR ), $\neg \; \{\backslash \; displaystyle\; \backslash \; neg\}$(НЕ ).

• Выражение (математика)
• Термин (логика)
• Контекстно-свободная грамматика
• Дерево синтаксического анализа
• Абстрактное синтаксическое дерево