Бинарное дерево без корня

A кладограмма в виде бинарного дерева без корней, отражающего сходство и историю эволюции видов актинобактерий.

В математике и информатике Бинарное дерево без корня - это дерево без корня , в котором каждая вершина имеет одного или трех соседей.

• 1 Определения
• 2 Связанные структуры
  • 2.1 Бинарные деревья с корнями
  • 2.2 Иерархическая кластеризация
  • 2.3 Эволюционные деревья
  • 2.4 Разложение по ветвям
• 3 Перечисление
• 4 Фундаментальные равенства
• 5 Альтернативные имена
• 6 Примечания
• 7 Ссылки

A свободное дерево или некорневое дерево - это подключенный неориентированный граф без циклов. Вершины с одним соседом - это листья дерева, а остальные вершины - внутренние узлы дерева. степень вершины - это количество ее соседей; в дереве с более чем одним узлом листья - это вершины первой степени. Бинарное дерево без корней - это свободное дерево, в котором все внутренние узлы имеют степень ровно три.

В некоторых приложениях может иметь смысл различать подтипы бинарных деревьев без корней: планарное вложение дерева может быть исправлено путем указания циклического порядка для ребер в каждой вершине, что делает его в плоское дерево . В информатике бинарные деревья часто имеют корень и упорядочиваются, когда они используются как структуры данных, но в приложениях неуправляемых бинарных деревьев в иерархической кластеризации и эволюционном дереве реконструкции, неупорядоченные деревья более распространены.

Кроме того, можно различать деревья, в которых все вершины имеют разные метки, деревья, в которых помечены только листья, и деревья, в которых узлы не помечены. В неуправляемом двоичном дереве с n листьями будет n - 2 внутренних узла, поэтому метки могут быть взяты из набора целых чисел от 1 до 2n - 1, когда все узлы должны быть помечены, или из набора целых чисел из От 1 до n, когда должны быть помечены только листья.

Бинарные деревья с корнями

Бинарное дерево T без корня может быть преобразовано в полностью корневое двоичное дерево (то есть корневое дерево, в котором каждый нелистовой узел имеет ровно два дочерних элемента), выбирая корневое ребро e для T, помещая новый корневой узел в середину e и направляя каждое ребро получившееся разделенное дерево далеко от корневого узла. И наоборот, любое двоичное дерево с полным корнем может быть преобразовано в двоичное дерево без корня путем удаления корневого узла, замены пути между двумя его дочерними элементами одним неориентированным ребром и подавления ориентации остальных ребер в графе. По этой причине существует ровно в 2n -3 раза больше бинарных деревьев с полным корнем и n листьев, чем некорневых двоичных деревьев с n листами.

Иерархическая кластеризация

A иерархическая кластеризация коллекции объекты могут быть формализованы как maximal семейство наборов объектов, в которых никакие два набора не пересекаются. То есть для каждых двух наборов S и T в семействе либо S и T не пересекаются, либо одно является подмножеством другого, и никакие другие наборы не могут быть добавлены к семейству при сохранении этого свойства. Если T - бинарное дерево без корней, оно определяет иерархическую кластеризацию своих листьев: для каждого ребра (u, v) в T существует кластер, состоящий из листьев, которые ближе к u, чем к v, и эти множества вместе с пустое множество и множество всех листьев образуют максимальное непересекающееся семейство. И наоборот, из любого максимального непересекающегося семейства множеств над набором из n элементов можно сформировать уникальное неукорененное двоичное дерево, которое имеет узел для каждой тройки (A, B, C) непересекающихся множеств в семействе, которые вместе покрывают все элементов.

Эволюционные деревья

Согласно простым формам теории эволюции, история жизни может быть представлена ​​в виде филогенетического дерева в котором каждый узел описывает вид, листья представляют виды, существующие сегодня, а края представляют отношения между предками и потомками между видами. Это дерево имеет естественную ориентацию от предков к потомкам и имеет корень у общего предка вида, так что это корневое дерево. Однако некоторые методы восстановления двоичных деревьев могут восстановить только узлы и ребра этого дерева, но не их ориентацию.

Например, кладистические методы, такие как максимальная экономия, используют в качестве данных набор двоичных атрибутов, описывающих особенности вида. Эти методы ищут дерево с заданными видами в виде листьев, в которых внутренние узлы также помечены характеристиками, и пытаются минимизировать количество раз, когда какой-либо элемент присутствует только в одной из двух конечных точек ребра в дереве. В идеале каждая функция должна иметь только одно ребро, для которого это так. Изменение корня дерева не меняет это количество различий краев, поэтому методы, основанные на экономии, не способны определить местоположение корня дерева и будут производить дерево без корня, часто не корень двоичное дерево.

Бинарные деревья без корней также создаются методами вывода эволюционных деревьев на основе данных квартета, определяющих для каждого четырехлистного вида неукорененное двоичное дерево, описывающее эволюцию этих четырех видов, и методами, использующими квартетное расстояние до измерять расстояние между деревьями.

Разбиение по ветвям

Бинарные деревья без корней также используются для определения разложения по ветвям графов путем формирования бинарного дерева без корней, листья которого представляют ребра данного графа. То есть разложение по ветвям можно рассматривать как иерархическую кластеризацию ребер графа. Разбиение ветвей и соответствующая числовая величина, ширина ветки, тесно связаны с шириной дерева и образуют основу для эффективных алгоритмов динамического программирования на графах.

Из-за их применения в иерархической кластеризации, наиболее естественная проблема перечисления графов для некорневых двоичных деревьев состоит в подсчете количества деревьев с n помеченными листьями и немаркированными внутренними узлами. Бинарное дерево без корней на n помеченных листьях может быть сформировано путем соединения n-го листа с новым узлом в середине любого из ребер двоичного дерева без корней на n - 1 помеченных листьях. Есть 2n - 5 ребер, к которым может быть прикреплен n-й узел; следовательно, количество деревьев на n листах больше, чем количество деревьев на n - 1 листе, в 2n - 5 раз. Таким образом, количество деревьев на n помеченных листьях равно двойному факториалу

$(\; 2\; п\; -\; 5)!\; !\; =\; (2\; п\; -\; 4)!\; (п\; -\; 2)!\; 2\; п\; -\; 2.\; \{\backslash \; displaystyle\; (2n-5)\; !!\; =\; \{\backslash \; frac\; \{(2n-4)!\}\; \{(n-2)!\; 2\; ^\; \{n-2\}\}\}.\}$

Количество деревьев на 2, 3, 4, 5,... обозначенные листья:

1, 1, 3, 15, 105, 945, 10395, 135135, 2027025, 34459425,... (последовательность A001147 в OEIS ).

Длина пути от листа к листу на фиксированном некорневом двоичном дереве (UBT) T кодирует количество ребер, принадлежащих уникальному пути в T, соединяющему данный лист с другой лист. Например, обращаясь к UBT, показанному на изображении справа, длина пути $p\; 1,\; 2\; \{\backslash \; displaystyle\; p\_\; \{1,2\}\}$между листьями 1 и 2 равно 2, тогда как длина пути $p\; 1,\; 3\; \{\backslash \; displaystyle\; p\_\; \{1,3\}\}$между листьями 1 и 3 равна 3. Последовательность длины пути от данного листа на фиксированном UBT T кодирует длины путей от данного листа ко всем оставшимся. Например, обращаясь к UBT, показанному на изображении справа, последовательность длины пути от листа 1 равно $p\; 1\; =\; (p\; 1,\; 2,\; p\; 1,\; 3,\; p\; 1,\; 4)\; =\; (2,\; 3,\; 3)\; \{\backslash \; displaystyle\; p\_\; \{1\}\; =\; (p\_\; \{1,2\},\; p\_\; \{1,3\},\; p\_\; \{1,4\})\; =\; (2,\; 3,3)\}$. Набор последовательностей длины пути, связанных с листами T, обычно называется набором последовательностей длины пути T.

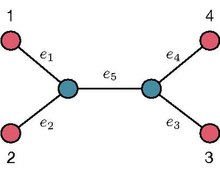Пример двоичного дерева без корней с четырьмя листьями

Даниэле Катандзаро и Лоуренс Уолси показал, что набор последовательностей длины пути, кодирующий данный UBT с n листьями, должен удовлетворять определенным равенствам, а именно

• $пи,\; я\; знак\; равно\; 0\; \{\backslash \; displaystyle\; p\_\; \{i,\; i\}\; =\; 0\}$для всех $i\; \in \; [1,\; n]\; \{\backslash \; displaystyle\; i\; \backslash \; in\; [1,\; n]\}$
• $pi,\; j\; =\; pj,\; i\; \{\backslash \; displaystyle\; p\_\; \{i,\; j\}\; =\; p\_\; \{j,\; i\}\}$для всех $i,\; j\; \in \; [1,\; n]:\; i\; \ne \; j\; \{\backslash \; displaystyle\; i,\; j\; \backslash \; in\; [1,\; n]:\; i\; \backslash \; neq\; j\}$
• $pi,\; i\; \le \; pi,\; k\; +\; pk,\; j\; \{\backslash \; displaystyle\; p\_\; \{i,\; i\}\; \backslash \; leq\; p\_\; \{i,\; k\}\; +\; p\_\; \{k,\; j\}\}$для всех $i,\; j,\; k\; \in \; [1,\; n]:\; я\; \ne \; j\; \ne \; k\; \{\backslash \; displaystyle\; i,\; j,\; k\; \backslash \; in\; [1,\; n]\; ]:\; я\; \backslash \; neq\; j\; \backslash \; neq\; k\}$
• $\sum \; j\; =\; 1\; n\; 1/2\; pi,\; j\; =\; 1/2\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; 1/2\; ^\; \{p\_\; \{\; i,\; j\}\}\; =\; 1/2\}$для всех $i\; \in \; [1,\; n]\; \{\backslash \; displaystyle\; i\; \backslash \; in\; [1,\; n]\}$(который является адаптация неравенства Крафт – Макмиллана )
• $\sum \; i\; =\; 1\; n\; \sum \; j\; =\; 1\; npi,\; j\; /\; 2\; pi,\; j\; =\; 2\; n\; -\; 3\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; p\_\; \{i,\; j\}\; /\; 2\; ^\; \{p\_\; \{i,\; j\}\}\; =\; 2n-3\; \}$, также называемое филогенетическим многообразием.

Доказано, что эти равенства необходимы и независимы для набора длин путей для кодирования UBT с n листами. В настоящее время неизвестно, достаточны ли они.

Бинарные деревья без корня также называются свободными бинарными деревьями, кубическими деревьями, троичными деревьями и тройные деревья без корней,. Однако имя «свободное двоичное дерево» также применялось к некорневым деревьям, которые могут иметь узлы второй степени, и к корневым двоичным деревьям с неупорядоченными дочерними элементами, а имя «троичное дерево» чаще используется для обозначения корневого дерево с тремя дочерними элементами на узел.

• Balding, DJ; Бишоп, Мартин Дж.; Каннингс, Кристофер (2007), Справочник по статистической генетике, 1 (3-е изд.), Wiley-Interscience, стр. 502, ISBN 978-0-470-05830-5.
• Килибрази, Руди; Витани, Пол М. (2006). «Новая эвристика квартетного дерева для иерархической кластеризации». arXiv : cs / 0606048..
• Чумадж, Артур; Гиббонс, Алан (1996), "Проблема Гатри: новые эквивалентности и быстрые сокращения", Теоретическая информатика, 154 (1): 3–22, doi : 10.1016 / 0304-3975 (95) 00126-3.
• Эппштейн, Дэвид (2009), «Квадратные штаны в дереве: сумма кластеризации поддеревьев и гиперболической декомпозиции штанов», Транзакции ACM по алгоритмам, 5 (3) : 1–24, arXiv : cs.CG/0604034, doi : 10.1145 / 1541885.1541890, S2CID 2434.
• Exoo, Джеффри (1996), «Простой метод построения небольших кубических графов обхватов 14, 15 и 16» (PDF), Electronic Journal of Combinatorics, 3 (1): R30, doi : 10.37236 / 1254.
• Furnas, George W. (1984), «Генерация случайных двоичных неупорядоченных деревьев», Journal of Classification, 1 (1): 187–233, doi : 10.1007 / BF01890123, S2CID 121121529.
• Харари, Фрэнк ; Palmer, E.M.; Робинсон, Р.В. (1992), «Подсчет свободных двоичных деревьев, допускающих заданную высоту» (PDF), Журнал комбинаторики, информации и системных наук, 17 : 175–181.
• Хенди, Майкл Д.; Пенни, Дэвид (1989), «Структура для количественного исследования эволюционных деревьев», Систематическая биология, 38 (4): 297–309, doi : 10.2307 / 2992396, JSTOR 2992396
• Przytycka, Teresa M.; Лармор, Лоуренс Л. (1994), «Повторное обращение к проблеме оптимального алфавитного дерева», Proc. 21-й Международный коллоквиум по автоматам, языкам и программированию (ICALP '94), Lecture Notes in Computer Science, 820, Springer-Verlag, pp. 251–262, doi : 10.1007 / 3-540-58201-0_73.
• Робертсон, Нил ; Сеймур, Пол Д. (1991), «Миноры графа. X. Препятствия для древовидной декомпозиции», Журнал комбинаторной теории, 52 (2): 153–190, doi : 10.1016 / 0095-8956 (91) 90061-N.
• ул. Джон, Кэтрин; Варноу, Тэнди ; Морет, Бернард М. Э. ; Фоутерд, Лиза (2003), «Исследование эффективности филогенетических методов: (невзвешенные) квартетные методы и объединение соседей» (PDF), Journal of Algorithms, 48 (1): 173 –193, doi : 10.1016 / S0196-6774 (03) 00049-X, S2CID 5550338.