Войти
В дифференциальной геометрии теорема о трех геодезических утверждает, что каждое риманово многообразие с топологией сферы имеет не менее трех замкнутых геодезических, образующих простые замкнутые кривые (т.е. без самопересечений). Результат также можно распространить на квазигеодезические на выпуклом многограннике.
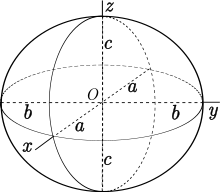Трехосный эллипсоид и его три геодезические A геодезические на римановой поверхности представляет собой кривую, локально прямую в каждой своей точке. Например, на евклидовой плоскости геодезические - это прямые, а на поверхности сферы геодезические - это большие круги. Кратчайший путь на поверхности между двумя точками всегда является геодезической, но могут существовать и другие геодезические. Геодезическая называется замкнутой геодезической, если она возвращается к своей начальной точке и начальному направлению; при этом он может креститься несколько раз. Теорема о трех геодезических гласит, что для поверхностей , гомеоморфных сфере, существуют по крайней мере три несамопересекающиеся замкнутые геодезические. Их может быть больше трех, например, сама сфера их бесконечно много.
Этот результат проистекает из математики океанской навигации, где поверхность Земли может быть точно смоделирована с помощью эллипсоида, и из изучения геодезических на эллипсоиде, кратчайшие пути для кораблей. В частности, почти сферический трехосный эллипсоид имеет только три простые замкнутые геодезические, свои экваторы. В 1905 году Анри Пуанкаре предположил, что каждая гладкая поверхность, топологически эквивалентная сфере, также содержит по крайней мере три простых замкнутых геодезических, а в 1929 году Лазар Люстерник и Лев Шнирельман опубликовал доказательство гипотезы, которое позже было признано ошибочным. Доказательство было восстановлено Гансом Вернером Баллманном в 1978 году.
Одно доказательство этой гипотезы исследует гомологии пространства гладких кривых на сфере и использует поток сокращения кривой для поиска простой замкнутой геодезической, представляющей каждый из трех нетривиальных классов гомологии этого пространства.
Усиленная версия теоремы утверждает, что, на любой римановой поверхности, которая является топологически сферой, обязательно существуют три простых замкнутых геодезических, длина которых не более чем пропорциональна диаметру поверхности.
Число замкнутых геодезических длины не более L на гладкой топологическая сфера растет пропорционально L / log L, но не все такие геодезические могут быть гарантированно простыми.
На компактных гиперболических римановых поверхностях существует бесконечно много простых замкнутых геодезических, но только конечное число с заданной границей длины. Они кодируются аналитически с помощью дзета-функции Сельберга. Скорость роста числа простых замкнутых геодезических в зависимости от их длины была исследована Марьям Мирзахани.
 | Нерешенная проблема в информатике :. Есть ли алгоритм, который может найти простую замкнутую квазигеодезическую на выпуклом многограннике за полиномиальное время? (другие нерешенные проблемы в информатике) |
Также возможно определить геодезические на некоторых поверхностях, которые не везде гладкие, например, выпуклые многогранники. Поверхность выпуклого многогранника имеет метрику, которая является локально евклидовой, за исключением вершин многогранника, а кривая, которая избегает вершин, является геодезической, если она проходит по прямым отрезкам внутри каждой грани многогранника и остается прямой поперек каждого ребра многогранника. что он пересекает. Хотя некоторые многогранники имеют простые замкнутые геодезические (например, правильный тетраэдр и дифеноиды имеют бесконечно много замкнутых геодезических, все простые), у других нет. В частности, простая замкнутая геодезическая выпуклого многогранника обязательно делит пополам полный угловой дефект вершин, а почти все многогранники не имеют таких биссектрис.
Тем не менее, теорема о трех геодезических может быть расширена на выпуклые многогранники, рассматривая квазигеодезические кривые, которые являются геодезическими за исключением вершин многогранников и имеют углы меньше π с обеих сторон в каждой пересекаемой вершине. Версия теоремы о трех геодезических для выпуклых многогранников утверждает, что все многогранники имеют по крайней мере три простых замкнутых квазигеодезических; это можно доказать, аппроксимируя многогранник гладкой поверхностью и применяя к этой поверхности теорему о трех геодезических. Это открытый вопрос, можно ли построить любую из этих квазигеодезических за полиномиальное время.
