Время остановки

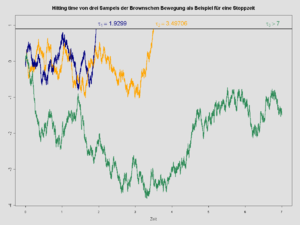
Чтобы узнать о музыкальном феномене, см. Время остановки. Пример времени остановки: а время удара по броуновское движение. Процесс начинается с 0 и останавливается, как только достигает 1.

В теории вероятностей, в частности при изучении случайных процессов, время остановки (также марковское время, марковский момент, необязательное время остановки или необязательное время) представляет собой особый тип «случайного времени»: случайная величина, значение которой интерпретируется как время, в которое данный случайный процесс демонстрирует интересующее поведение. Время остановки часто определяется правилом остановки, механизмом для принятия решения о продолжении или остановке процесса на основе текущего положения и прошлых событий, и которое почти всегда приводит к решению остановиться в какой-то конечный момент времени.

Время остановки встречается в теории принятия решений, и теорема о необязательной остановке является важным результатом в этом контексте. Моменты остановки также часто используются в математических доказательствах, чтобы «приручить континуум времени», как выразился Чанг в своей книге (1982).

• 1 Определение
  • 1.1 Дискретное время
  • 1.2 Общий случай
  • 1.3 Как адаптированный процесс
  • 1.4 Комментарии
• 2 Примеры
• 3 Локализация
• 4 типа времени остановки
• 5 Правила остановки в клинических испытаниях
• 6 См. Также
• 7 ссылки
  • 7.1 Дальнейшее чтение

Дискретное время

Позвольте быть случайной величиной, которая определена на фильтрованном вероятностном пространстве со значениями в. Тогда называется моментом остановки (по отношению к фильтрации ), если выполняется следующее условие: ${\ Displaystyle \ тау}$ ${\ displaystyle (\ Omega, {\ mathcal {F}}, ({\ mathcal {F}} _ {n}) _ {n \ in \ mathbb {N}}, P)}$${\ Displaystyle \ mathbb {N} \ чашка \ {+ \ infty \}}$${\ Displaystyle \ тау}$ ${\ Displaystyle \ mathbb {F} = (({\ mathcal {F}} _ {п}) _ {п \ in \ mathbb {N}}}$

${\ Displaystyle \ {\ тау = п \} \ ин {\ mathcal {F}} _ {п}}$ для всех ${\ displaystyle n}$

Интуитивно это условие означает, что «решение» о том, остановиться ли во время, должно основываться только на информации, имеющейся в данный момент, а не на какой-либо информации в будущем. ${\ displaystyle n}$${\ displaystyle n}$

Общий случай

Позвольте быть случайной величиной, которая определена на фильтрованном вероятностном пространстве со значениями в. В большинстве случаев. Тогда называется моментом остановки (по отношению к фильтрации ), если выполняется следующее условие: ${\ Displaystyle \ тау}$ ${\ displaystyle (\ Omega, {\ mathcal {F}}, ({\ mathcal {F}} _ {t}) _ {t \ in T}, P)}$${\ displaystyle T}$${\ Displaystyle Т = [0, + \ infty)}$${\ Displaystyle \ тау}$ ${\ Displaystyle \ mathbb {F} = ({\ mathcal {F}} _ {т}) _ {т \ in T}}$

${\ displaystyle \ {\ tau \ leq t \} \ in {\ mathcal {F}} _ {t}}$ для всех ${\ displaystyle t \ in T}$

Как адаптированный процесс

Позвольте быть случайной величиной, которая определена на фильтрованном вероятностном пространстве со значениями в. Тогда время остановки называется моментом остановки, если случайный процесс определяется формулой ${\ Displaystyle \ тау}$ ${\ displaystyle (\ Omega, {\ mathcal {F}}, ({\ mathcal {F}} _ {t}) _ {t \ in T}, P)}$${\ displaystyle T}$${\ Displaystyle \ тау}$ ${\ displaystyle X = (X_ {t}) _ {t \ in T}}$

${\ displaystyle X_ {t}: = {\ begin {cases} 1 amp; {\ text {if}} t lt;\ tau \\ 0 amp; {\ text {if}} t \ geq \ tau \ end {cases}}}$

будет адаптирован к фильтрации${\ Displaystyle \ mathbb {F} = ({\ mathcal {F}} _ {т}) _ {т \ in T}}$

Комментарии

Некоторые авторы явно исключают случаи, когда это возможно, тогда как другие авторы разрешают принимать любое значение при закрытии. ${\ Displaystyle \ тау}$${\ displaystyle + \ infty}$${\ Displaystyle \ тау}$${\ displaystyle T}$

Чтобы проиллюстрировать некоторые примеры случайных моментов, когда правила останавливаются, а некоторые - нет, рассмотрим игрока, играющего в рулетку с типичным преимуществом казино, начиная со 100 долларов и делая ставку 1 доллар на красное в каждой игре:

• Ровно пять игр соответствуют времени остановки τ  = 5 и являются правилом остановки.
• Играть до тех пор, пока у него не закончатся деньги или не сыграет 500 игр, является правилом остановки.
• Игра до тех пор, пока он не достигнет максимальной суммы впереди, не является правилом остановки и не предусматривает время остановки, поскольку требует информации о будущем, а также о настоящем и прошлом.
• Игра до тех пор, пока он не удвоит свои деньги (занимая при необходимости), не является правилом остановки, поскольку существует положительная вероятность того, что он никогда не удвоит свои деньги.
• Игра до тех пор, пока он либо не удвоит свои деньги, либо не закончатся деньги, является правилом остановки, даже несмотря на то, что потенциально нет ограничений на количество игр, которые он играет, поскольку вероятность того, что он остановится через конечное время, равна 1.

Чтобы проиллюстрировать более общее определение остановки времени, рассмотрим броуновское движение, которое представляет собой случайный процесс, каждая из которых является случайной величиной, определенной в вероятностном пространстве. Мы определяем фильтрацию на этом вероятностном пространстве, позволяя быть σ -алгеброй, порожденной всеми множествами вида где и является борелевским множеством. Интуитивно, событие E происходит тогда и только тогда, когда мы можем определить, является ли E истинным или ложным, просто наблюдая за броуновским движением от времени 0 до момента t. ${\ Displaystyle (В_ {т}) _ {т \ geq 0}}$${\ displaystyle B_ {t}}$${\ Displaystyle (\ Omega, {\ mathcal {F}}, \ mathbb {P})}$${\ displaystyle {\ mathcal {F}} _ {t}}$${\ Displaystyle (В_ {s}) ^ {- 1} (А)}$${\ displaystyle 0 \ leq s \ leq t}$${\ Displaystyle А \ substeq \ mathbb {R}}$ ${\ displaystyle {\ mathcal {F}} _ {t}}$

• Каждая константа (тривиально) является моментом остановки; это соответствует правилу остановки «остановить время ».${\ displaystyle \ tau: = t_ {0}}$${\ displaystyle t_ {0}}$
• Пусть Then - время остановки для броуновского движения, соответствующее правилу остановки: «остановитесь, как только броуновское движение превысит значение a ».${\ displaystyle a \ in \ mathbb {R}.}$${\ Displaystyle \ тау: = \ инф \ {т \ geq 0 \ середина B_ {т}gt; а \}}$
• Другое время остановки дается. Это соответствует правилу остановки «остановитесь, как только броуновское движение станет положительным на непрерывном участке длиной 1 единицу времени».${\ displaystyle \ tau: = \ inf \ {t \ geq 1 \ mid B_ {s}gt; 0 {\ text {для всех}} s \ in [t-1, t] \}}$
• В общем, если τ 1 и τ 2 являются временами остановки, то их минимум, их максимум и их сумма τ 1  +  τ 2 также являются временами остановки. (Это не относится к различиям и продуктам, потому что они могут потребовать «заглянуть в будущее», чтобы определить, когда остановиться.)${\ displaystyle \ left (\ Omega, {\ mathcal {F}}, \ left \ {{\ mathcal {F}} _ {t} \ right \} _ {t \ geq 0}, \ mathbb {P} \ Правильно)}$${\ Displaystyle \ тау _ {1} \ клин \ тау _ {2}}$${\ Displaystyle \ тау _ {1} \ ви \ тау _ {2}}$

Время попадания, подобное приведенному выше второму примеру, может быть важным примером времени остановки. В то время как относительно просто показать, что по существу все времена остановки - это времена попадания, может быть намного сложнее показать, что определенное время достижения является временем остановки. Результаты последнего типа известны как теорема Дебю.

Моменты остановки часто используются для обобщения определенных свойств случайных процессов на ситуации, в которых требуемое свойство выполняется только в локальном смысле. Во-первых, если X - процесс, а τ - время остановки, то X ^τ используется для обозначения процесса X, остановленного в момент τ.

${\ Displaystyle X_ {т} ^ {\ тау} = Икс _ {\ мин (т, \ тау)}}$

Тогда говорят, что X локально удовлетворяет некоторому свойству P, если существует последовательность моментов остановки τ n, которая возрастает до бесконечности и для которой процессы

${\ displaystyle \ mathbf {1} _ {\ {\ tau _ {n}gt; 0 \}} X ^ {\ tau _ {n}}}$

удовлетворяет свойство P. Типичные примеры с набором временного индекса I = [0, ∞) следующие:

Процесс местного мартингейла. Процесс X является локальным мартингалом, если он càdlàg и существует последовательность моментов остановки τ n, возрастающая до бесконечности, такая, что

${\ displaystyle \ mathbf {1} _ {\ {\ tau _ {n}gt; 0 \}} X ^ {\ tau _ {n}}}$

является мартингалом для каждого n.

Локально интегрируемый процесс. Неотрицательный и возрастающий процесс X является локально интегрируемым, если существует последовательность моментов остановки τ n, возрастающих до бесконечности, такая, что

${\ Displaystyle \ OperatorName {E} \ left [\ mathbf {1} _ {\ {\ tau _ {n}gt; 0 \}} X ^ {\ tau _ {n}} \ right] lt;\ infty}$

для каждого n.

Моменты остановки с установленным индексом времени I = [0, ∞) часто делятся на один из нескольких типов в зависимости от того, можно ли предсказать, когда они вот-вот произойдут.

Время остановки τ является предсказуемым, если она равна пределом возрастающей последовательности моментов остановки т п, удовлетворяющий т п lt; т, когда τ gt; 0. Последовательности τ п называется объявить τ и предсказуемые времена остановочных иногда называют анонсируемый. Примерами прогнозируемого времени остановки являются время срабатывания непрерывных и адаптированных процессов. Если τ - это первый раз, когда непрерывный и вещественнозначный процесс X равен некоторому значению a, то он объявляется последовательностью τ n, где τ n - первый раз, когда X находится на расстоянии 1 / n из.

Доступное время остановки - это время, которое может быть покрыто последовательностью предсказуемых времен. То есть время остановки τ доступно, если P ( τ = τ n для некоторого n) = 1, где τ n - предсказуемые времена.

Стопорное время τ является абсолютно недоступным, если она никогда не может быть объявлена возрастающей последовательностью времени остановки. Эквивалентно, P ( τ = σ lt;∞) = 0 для каждого предсказуемого времени σ. Примеры полностью недоступных времен остановки включают времена скачков пуассоновских процессов.

Каждый момент остановки τ можно однозначно разложить на доступное и полностью недоступное время. То есть существует единственное доступное время остановки σ и полностью недоступное время υ такие, что τ = σ, если σ lt;∞, τ = υ, если υ lt;∞, и τ = ∞, если σ = υ = ∞. Обратите внимание, что в формулировке этого результата разложения времена остановки не обязательно должны быть почти наверняка конечными и могут равняться ∞.

Клинические испытания в медицине часто проводят промежуточный анализ, чтобы определить, достигло ли испытание своих конечных результатов. Однако промежуточный анализ создает риск ложноположительных результатов, и поэтому границы остановки используются для определения количества и времени промежуточного анализа (также известного как альфа-расход, чтобы обозначить частоту ложноположительных результатов). В каждом из R промежуточных тестов испытание останавливается, если вероятность ниже порогового значения p, которое зависит от используемого метода. См. Последовательный анализ.

• Оптимальная остановка
• Алгоритм коэффициентов
• Секретарь проблема
• Время попадания
• Остановленный процесс
• Проблема расстройства
• Теорема Дебю
• Последовательный анализ

дальнейшее чтение

• Томас С. Фергюсон, «Кто решил проблему секретаря?», Stat. Sci. т. 4, 282–296, (1989).
• Введение в время остановки.
• Ф. Томас Брюсс, «Суммируйте шансы до единицы и остановитесь», Annals of Probability, Vol. 4, 1384–1391, (2000)
• Чунг, Кай Лай (1982). Лекции от марковских процессов до броуновского движения. Grundlehren der Mathematischen Wissenschaften No. 249. Нью-Йорк: Springer-Verlag. ISBN   978-0-387-90618-8.
• Х. Винсент Пур и Олимпия Хаджилиадис (2008). Самое быстрое обнаружение (Первое издание). Кембридж: Издательство Кембриджского университета. ISBN   978-0-521-62104-5.
• Проттер, Филип Э. (2005). Стохастическое интегрирование и дифференциальные уравнения. Стохастическое моделирование и прикладная вероятность № 21 (Второе издание (версия 2.1, исправленное третье издание) изд.). Берлин: Springer-Verlag. ISBN   978-3-540-00313-7.
• Ширяев, Альберт Н. (2007). Оптимальные правила остановки. Springer. ISBN   978-3-540-74010-0.