Радиус устойчивости

Радиус устойчивости объекта (системы, функции, матрицы, параметра) в заданной номинальной точке равен радиусу наибольшего мяч с центром в номинальной точке, все элементы которого удовлетворяют заранее заданным условиям устойчивости. Картина этого интуитивного понятия такова:

где $p\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{p\}\}\}$обозначает номинальную точку, $P\; \{\backslash \; displaystyle\; P\}$обозначает пространство всех возможных значений объекта $p\; \{\backslash \; displaystyle\; p\}$и заштрихованной области $P\; (s)\; \{\backslash \; displaystyle\; P\; (s)\; \}$представляет набор точек, удовлетворяющих условиям устойчивости. Радиус синего круга, показанного красным, - это радиус устойчивости.

• 1 Абстрактное определение
• 2 История
• 3 Связь с моделью максимина Уолда
• 4 Теория принятия решений по информационным пробелам
• 5 Альтернативное определение
• 6 Радиус устойчивости функций
  • 6.1 Определение
  • 6.2 Приложения
  • 6.3 Свойства
  • 6.4 Примеры
• 7 См. Также
• 8 Ссылки

Формальное определение этого понятия варьируется в зависимости от Область применения. Очень полезно следующее абстрактное определение

$\rho \; ^\; (p\; ^):\; =\; max\; \{\rho \; \ge \; 0:\; p\; \in \; P\; (s),\; \forall \; p\; \in \; B\; (\rho ,\; p\; ^)\}\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; rho\}\}\; (\{\backslash \; hat\; \{p\}\}):\; =\; \backslash \; max\; \backslash \; \backslash \; \{\backslash \; rho\; \backslash \; geq\; 0:\; p\; \backslash \; in\; P\; (s),\; \backslash \; forall\; p\; \backslash \; in\; B\; (\backslash \; rho,\; \{\backslash \; hat\; \{p\}\}))\; \backslash \}\}$

где $B\; (\rho ,\; p\; ^)\; \{\backslash \; displaystyle\; B\; (\backslash \; rho,\; \{\backslash \; hat\; \{p\}\})\}$обозначает закрытый шар радиуса $\rho \; \{\backslash \; displaystyle\; \backslash \; rho\}$в $P\; \{\backslash \; displaystyle\; P\}$с центром в $p\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{p\; \}\}\}$.

Похоже, концепция была изобретена в начале 1960-х. В 80-е годы он стал популярным в теории управления и оптимизации. Он широко используется в качестве модели локальной устойчивости к небольшим возмущениям заданной номинальной стоимости интересующего объекта.

Было показано, что модель радиуса устойчивости является примером модели максимина Вальда. То есть

$max\; \{\rho \; \ge \; 0:\; p\; \in \; P\; (s),\; \forall \; p\; \in \; B\; (\rho ,\; p\; ^)\}\; \equiv \; max\; \rho \; \ge \; 0\; min\; p\; \in \; B\; (\rho ,\; p\; ^)\; f\; (\rho ,\; p)\; \{\backslash \; displaystyle\; \backslash \; max\; \backslash \; \backslash \; \{\backslash \; rho\; \backslash \; geq\; 0:\; p\; \backslash \; in\; P\; (s),\; \backslash \; forall\; p\; \backslash \; in\; B\; (\backslash \; rho,\; \{\backslash \; hat\; \{p\}\})\; \backslash \}\; \backslash \; Equiv\; \backslash \; max\; \_\; \{\backslash \; rho\; \backslash \; geq\; 0\}\; \backslash \; min\; \_\; \{p\; \backslash \; in\; B\; (\backslash \; rho,\; \{\backslash \; hat\; \{p\}\})\}\; f\; (\backslash \; rho,\; p)\}$

где

$f\; (\rho ,\; p)\; =\; \{\rho ,\; п\; \in \; п\; (s)\; -\; \infty ,\; п\; \notin \; п\; (s)\; \{\backslash \; displaystyle\; f\; (\backslash \; rho,\; p)\; =\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{array\}\; \{cc\}\; \backslash \; rho,\; \backslash \; p\; \backslash \; in\; P\; (\; s)\; \backslash \backslash \; -\; \backslash \; infty,\; \backslash \; p\; \backslash \; notin\; P\; (s)\; \backslash \; end\; \{array\}\}\; \backslash \; right.\}$

Большой штраф ($-\; \infty \; \{\backslash \; displaystyle\; -\; \backslash \; infty\}$) - это устройство, заставляющее игрока $max\; \{\backslash \; displaystyle\; \backslash \; max\}$не нарушать номинальное значение за пределами радиуса устойчивости системы. Это показатель того, что модель устойчивости является моделью локальной стабильности / устойчивости, а не глобальной.

Теория принятия решений по информационным промежуткам - это недавняя теория не вероятностных решений. Утверждается, что он радикально отличается от всех современных теорий принятия решений в условиях неопределенности. Но было показано, что его модель устойчивости, а именно

$\alpha \; ^\; (q,\; u\; ~):\; =\; max\; \{\alpha \; \ge \; 0:\; rc\; \le \; R\; (q,\; u),\; \forall \; u\; \in \; U\; (\alpha ,\; u\; ~)\}\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; (q,\; \{\backslash \; тильда\; \{u\}\}):\; =\; \backslash \; max\; \backslash \; \backslash \; \{\backslash \; alpha\; \backslash \; geq\; 0:\; r\_\; \{c\}\; \backslash \; leq\; R\; (q,\; u),\; \backslash \; forall\; u\; \backslash \; in\; U\; (\backslash \; alpha,\; \{\backslash \; tilde\; \{u\}\})\; \backslash \}\}$

на самом деле является моделью радиуса устойчивости, характеризующейся простым требованием устойчивости вида $rc\; \le \; R\; (q,\; u)\; \{\backslash \; displaystyle\; r\_\; \{c\}\; \backslash \; leq\; R\; (q,\; u)\}$где $q\; \{\backslash \; displaystyle\; q\}$обозначает рассматриваемое решение, $u\; \{\backslash \; displaystyle\; u\; \}$обозначает интересующий параметр, $u\; ~\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{u\}\}\}$обозначает оценку истинного значения $u\; \{\backslash \; displaystyle\; u\}$и $U\; (\alpha ,\; u\; ~)\; \{\backslash \; displaystyle\; U\; (\backslash \; alpha,\; \{\backslash \; tilde\; \{u\}\})\}$обозначает шар радиуса $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$с центром в $u\; ~\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{u\}\}\}$.

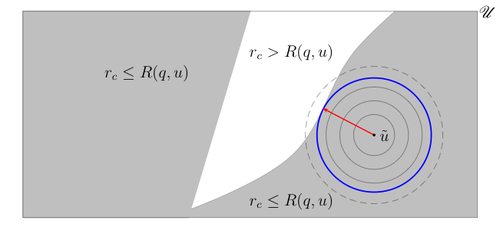
Поскольку модели радиуса устойчивости предназначены для работы с небольшими отклонениями от номинального значения параметр, я Модель устойчивости nfo-gap измеряет локальную устойчивость решений в окрестности оценки $u\; ~\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{u\}\}\}$.

Сниедович утверждает, что по этой причине теория не подходит для рассмотрения серьезная неопределенность, характеризующаяся плохой оценкой и обширным пространством неопределенности.

Бывают случаи, когда удобнее определять радиус устойчивости несколько иначе. Например, во многих приложениях в теории управления радиус устойчивости определяется как величина наименьшего дестабилизирующего возмущения номинального значения интересующего параметра. Картинка такая:

Формально,

$\rho \; ^\; (q):\; =\; min\; p\; \notin \; P\; (s)\; dist\; (p,\; p\; ^)\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; rho\}\}\; (q):\; =\; \backslash \; min\; \_\; \{p\; \backslash \; notin\; P\; (s)\}\; dist\; (p,\; \{\backslash \; hat\; \{p\}\})\}$

где $dist\; (p,\; p\; ^)\; \{\backslash \; displaystyle\; dist\; (p,\; \{\backslash \; hat\; \{p\}\})\}$обозначает расстояние $p\; \in \; P\; \{\backslash \; displaystyle\; p\; \backslash \; in\; P\}$от $p\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{p\; \}\}\}$.

Радиус устойчивости непрерывной функции f (в ​​функциональном пространстве F) с по отношению к открытой области устойчивости D - это расстояние между f и набором нестабильных функций (относительно D). Мы говорим, что функция стабильна относительно D, если ее спектр находится в D. Здесь понятие спектра определяется в каждом конкретном случае, как объясняется ниже.

Определение

Формально, если мы обозначим множество стабильных функций через S (D) и радиус устойчивости через r (f, D), то:

$r\; (f,\; D)\; знак\; равно\; inf\; g\; \in \; C\; \{\Vert \; g\; \Vert :\; е\; +\; g\; \notin \; S\; (D)\},\; \{\backslash \; displaystyle\; r\; (f,\; D)\; =\; \backslash \; inf\; \_\; \{g\; \backslash \; in\; C\}\; \backslash \; \{\backslash \; |\; g\; \backslash \; |:\; f\; +\; g\; \backslash \; notin\; S\; (D)\; \backslash \},\}$

где C - подмножество F.

Обратите внимание, что если f уже нестабильно (относительно D), то r (f, D) = 0 (если C содержит ноль).

Приложения

Понятие радиуса устойчивости обычно применяется к специальным функциям как полиномы (тогда спектр является корнями) и матрицы (спектр - это собственные значения ). Случай, когда C является правильным подмножеством F, позволяет нам рассматривать структурированные возмущения (например, для матрицы нам могут потребоваться возмущения только в последней строке). Это интересная мера устойчивости, например, в теории управления.

Свойства

Пусть f будет (комплексным ) многочленом степени n, C = F будет множеством многочленов степени меньше (или равной) n (которые мы идентифицируем здесь с набором $C\; n\; +\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{C\}\; ^\; \{n\; +\; 1\}\}$коэффициентов). В качестве D возьмем открытый единичный круг, что означает, что мы ищем расстояние между многочленом и набором стабильных многочленов Шура . Тогда:

$r\; (f,\; D)\; =\; inf\; z\; \in \; \partial \; D\; |\; f\; (z)\; |\; \Vert \; Q\; (Z)\; \Vert ,\; \{\backslash \; Displaystyle\; г\; (е,\; D)\; =\; \backslash \; inf\; \_\; \{z\; \backslash \; in\; \backslash \; partial\; D\}\; \{\backslash \; frac\; \{|\; f\; (z)\; |\}\; \{\backslash \; |\; q\; (z)\; \backslash \; |\}\},\}$

где q содержит каждый базисный вектор (например, $q\; (z)\; =\; (1,\; z,\dots ,\; zn)\; \{\backslash \; displaystyle\; q\; (z)\; =\; (1,\; z,\; \backslash \; ldots,\; z\; ^\; \{n\; \})\}$, когда q - обычное степенное основание). Этот результат означает, что радиус устойчивости ограничен минимальным значением, которого f достигает на единичной окружности.

Примеры

• Многочлен $f\; (z)\; =\; z\; 8–9\; /\; 10\; \{\backslash \; displaystyle\; f\; (z)\; =\; z\; ^\; \{8\}\; -9/10\}$(нули которого являются корнями 8-й степени из 0,9) имеет радиус устойчивости 1/80, если q - степенной базис, а норма - бесконечная норма. Таким образом, должен существовать многочлен g с (бесконечной) нормой 1/90 такой, что f + g имеет (по крайней мере) корень на единичной окружности. Такой ag имеет вид, например, $g\; (z)\; =\; -\; 1/90\; =\; i\; =\; 0\; 8\; zi\; \{\backslash \; displaystyle\; g\; (z)\; =\; -\; 1/90\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{8\}\; z\; ^\; \{\; i\}\}$. В самом деле, (f + g) (1) = 0 и 1 находится на единичной окружности, что означает, что f + g нестабильно.

• стабильный многочлен
• модель максимина Вальда

1. ^Злобец С. (2009). Недифференцируемая оптимизация: параметрическое программирование. Стр. 2607-2615, в Encyclopedia of Optimization, Floudas C.A, Pardalos, P.M. редакторы, Springer.
2. ^ Сниедович, М. (2010). Взгляд с высоты на теорию принятия решений по информационным пробелам. Журнал «Финансирование рисков», 11 (3), 268-283.
3. ^Уилф, Х.С. (1960). Максимально устойчивое численное интегрирование. Журнал Общества промышленной и прикладной математики, 8 (3), 537-540.
4. ^Милн, У.Э., и Рейнольдс, Р.Р. (1962). Методы пятого порядка численного решения обыкновенных дифференциальных уравнений. Журнал АКМ, 9 (1), 64-70.
5. ^Хиндрихсен, Д., Притчард, А.Дж. (1986). Радиусы устойчивости линейных систем, Системы и письма управления, 7, 1-10.
6. ^Злобец С. (1988). Характеристика оптимальности в моделях математического программирования. Acta Applicandae Mathematicae, 12, 113–180.
7. ^Пэйс А.Д.Б. и Вирт, Ф. (1998). Анализ локальной робастности устойчивости течений. Математика управления, сигналов и систем, 11, 289-302.