Ценовое уравнение

Описание того, как признак или ген изменяется по частоте с течением времени

В теории эволюции и естественный отбор, уравнение цены (также известное как уравнение Прайса или теорема Прайса ) описывает, как признак или аллель изменяется по частоте со временем. Уравнение использует ковариацию между признаком и приспособленностью, чтобы дать математическое описание эволюции и естественного отбора. Это дает возможность понять влияние передачи генов и естественного отбора на частоту аллелей в каждом новом поколении популяции. Уравнение Прайса было выведено Джорджем Р. Прайсом, работая в Лондоне над повторным выводом W.D. Гамильтон работает над родственной селекцией. Примеры уравнения Прайса были построены для различных эволюционных случаев. Уравнение Прайса также имеет приложения в экономике.

. Важно отметить, что уравнение Прайса не является физическим или биологическим законом. Это не краткое или общее выражение экспериментально подтвержденных результатов. Это скорее чисто математическая взаимосвязь между различными статистическими дескрипторами динамики населения. Это математически достоверно и поэтому не подлежит экспериментальной проверке. Проще говоря, это математическое повторение выражения «выживание наиболее приспособленных», которое на самом деле самоочевидно, учитывая математические определения «выживания» и «наиболее приспособленных».

• 1 Утверждение
• 2 Доказательство
  • 2.1 Вывод уравнения цены в непрерывном времени
• 3 Простое уравнение цены
  • 3.1 Приложения
  • 3.2 Динамическая достаточность и простое уравнение цены
• 4 Уравнение полной цены
  • 4.1 Соответствие генотипу
  • 4.2 Соответствие происхождению
• 5 Критика
• 6 Культурные ссылки
• 7 См. Также
• 8 Ссылки
• 9 Дополнительная литература

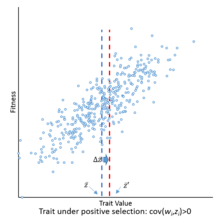
Пример признака при положительном отборе

Уравнение Прайса показывает, что изменение среднего количества $z\; \{\backslash \; displaystyle\; z\}$признака в популяции от одного поколения к другому следующий ($\Delta \; z\; \{\backslash \; displaystyle\; \backslash \; Delta\; z\}$) определяется ковариацией между суммами $zi\; \{\backslash \; displaystyle\; z\_\; \{i\}\}$признака для субпопуляции $i\; \{\backslash \; displaystyle\; i\}$и соответствия $wi\; \{\backslash \; displaystyle\; w\_\; \{i\}\}$субпопуляций вместе с ожидаемое изменение величины значения признака из-за приспособленности, а именно $E\; (w\; я\; \Delta \; zi)\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{E\}\; (w\_\; \{i\}\; \backslash \; Delta\; z\_\; \{i\})\}$:

$\Delta \; z\; =\; 1\; w\; cov\; \; (wi,\; zi)\; +\; 1\; вес\; E\; \; (wi\; \Delta \; zi).\; \{\backslash \; displaystyle\; \backslash \; Delta\; \{z\}\; =\; \{\backslash \; frac\; \{1\}\; \{w\}\}\; \backslash \; operatorname\; \{cov\}\; (w\_\; \{i\},\; z\_\; \{i\})\; +\; \{\backslash \; frac\; \{1\}\; \{w\}\}\; \backslash \; operatorname\; \{E\; \}\; (w\_\; \{i\}\; \backslash ,\; \backslash \; Delta\; z\_\; \{i\}).\}$

Здесь $w\; \{\backslash \; displaystyle\; w\}$- средний показатель пригодности по совокупности, а $E\; \{\; \backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\}$и $cov\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{cov\}\}$представляют среднее значение генеральной совокупности и ковариацию соответственно. 'Фитнес' $w\; \{\backslash \; displaystyle\; w\}$- отношение среднего количества потомков для всей популяции к количеству взрослых особей в популяции, и $wi\; \{\backslash \; displaystyle\; w\_\; \{i\}\}$- такое же соотношение только для субпопуляции $i\; \{\backslash \; displaystyle\; i\}$.

Термин ковариации отражает эффекты естественного отбора; если ковариация между приспособленностью ($wi\; \{\backslash \; displaystyle\; w\_\; \{i\}\}$) и значением признака ($zi\; \{\backslash \; displaystyle\; z\_\; \{i\}\}$) равна положительный, то прогнозируется, что значение признака будет увеличиваться в среднем по популяции $i\; \{\backslash \; displaystyle\; i\}$. Если ковариация отрицательная, то признак вреден и, по прогнозам, будет уменьшаться по частоте.

Второй член, $E\; (wi\; \Delta \; zi)\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{E\}\; (w\_\; \{i\}\; \backslash \; Delta\; z\_\; \{i\})\}$, представляет другие факторы чем прямой отбор, который может повлиять на эволюцию признака. Этот термин может включать генетический дрейф, мутацию смещение или мейотический драйв. Кроме того, этот термин может охватывать эффекты многоуровневого выбора или группового выбора.

Прайс (1972), названный им термином «изменение среды», и обозначил оба термина с использованием обозначения частной производной (∂ NS и ∂ EC). Это понятие окружающей среды включает межвидовые и экологические эффекты. Прайс описывает это следующим образом:

Фишер принял несколько необычную точку зрения, рассматривая доминирование и эпистаз как эффекты среды. Например, он пишет (1941): «Изменение пропорции любой пары генов само по себе представляет собой изменение среды, в которой находятся особи данного вида». Поэтому он считал, что влияние естественного отбора на М ограничивается аддитивные или линейные эффекты изменений частот генов, в то время как все остальное - доминирование, эпистаз, популяционное давление, климат и взаимодействия с другими видами - он считал вопросом окружающей среды.

— GR Прайс (1972), фундаментальная теорема Фишера прояснила

Предположим, что существует популяция из $n\; \{\backslash \; displaystyle\; n\}$особей, у которых количество конкретной характеристики меняется. Эти $n\; \{\backslash \; displaystyle\; n\}$индивидуумы могут быть сгруппированы по количеству характеристик, которые отображает каждый. Может быть всего одна группа из всех $n\; \{\backslash \; displaystyle\; n\}$индивидов (состоящая из одного общего значения характеристики) и целых $n\; \{\backslash \; displaystyle\; n\; \}$группы по одному человеку в каждой (состоящие из $n\; \{\backslash \; displaystyle\; n\}$различных значений характеристики). Проиндексируйте каждую группу с помощью $i\; \{\backslash \; displaystyle\; i\}$так, чтобы количество членов в группе было $ni\; \{\backslash \; displaystyle\; n\_\; \{i\}\}$и значение характеристики, общей для всех членов группы, составляет $zi\; \{\backslash \; displaystyle\; z\_\; \{i\}\}$. Теперь предположим, что наличие $zi\; \{\backslash \; displaystyle\; z\_\; \{i\}\}$характеристики связано с наличием fitness $wi\; \{\backslash \; displaystyle\; w\_\; \{i\}\}$где продукт $wini\; \{\backslash \; displaystyle\; w\_\; \{i\}\; n\_\; \{i\}\}$представляет количество потомков в следующем поколении. Обозначьте это количество потомков из группы $i\; \{\backslash \; displaystyle\; i\}$как $ni\; \prime \; \{\backslash \; displaystyle\; n\_\; \{i\}\; \text{'}\}$так, чтобы $wi\; =\; ni\; \prime \; /\; ni\; \{\backslash \; displaystyle\; w\_\; \{i\}\; =\; n\_\; \{i\}\; \text{'}/\; n\_\; \{i\}\}$. Пусть $zi\; \prime \; \{\backslash \; displaystyle\; z\_\; \{i\}\; \text{'}\}$будет средней величиной характеристики, отображаемой потомком из группы $i\; \{\backslash \; displaystyle\; i\}$. Обозначим величину изменения характеристики в группе $i\; \{\backslash \; displaystyle\; i\}$как $\Delta \; zi\; \{\backslash \; displaystyle\; \backslash \; Delta\; z\_\; \{i\}\}$, определенную как

$\Delta \; zi\; =\; defzi\; \prime \; -\; zi\; \{\backslash \; displaystyle\; \backslash \; Delta\; \{z\_\; \{i\}\}\; \backslash ;\; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{=\}\}\; \backslash ;\; z\_\; \{i\}\; \text{'}-\; z\_\; \{i\}\}$

Теперь возьмем $z\; \{\backslash \; displaystyle\; z\}$как среднее значение характеристики в этой совокупности, а $z\; \prime \; \{\backslash \; displaystyle\; z\; \text{'}\}$как среднюю характеристику ценность в следующем поколении. Определите изменение средней характеристики как $\Delta \; z\; \{\backslash \; displaystyle\; \backslash \; Delta\; \{z\}\}$. То есть

$\Delta \; z\; =\; defz\; \prime \; -\; z\; \{\backslash \; displaystyle\; \backslash \; Delta\; \{z\}\; \backslash ;\; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{=\}\}\; \backslash ;\; z\text{'}-z\}$

Обратите внимание, что это не является средним значением $\Delta \; zi\; \{\backslash \; displaystyle\; \backslash \; Delta\; \{z\_\; \{i\}\}\}$(поскольку возможно, что $ni\; \ne \; ni\; \prime \; \{\backslash \; displaystyle\; n\_\; \{i\}\; \backslash \; neq\; n\; \text{'}\_\; \{i\}\}$). Также возьмите $w\; \{\backslash \; displaystyle\; w\}$как среднюю приспособленность этой совокупности. Уравнение Прайса гласит:

$w\; \Delta \; z\; =\; cov\; \; (wi,\; zi)\; +\; E\; \; (wi\; \Delta \; zi)\; \{\backslash \; displaystyle\; w\; \backslash ,\; \backslash \; Delta\; \{z\}\; =\; \backslash \; operatorname\; \{cov\}\; (w\_\; \{i\},\; z\_\; \{i\})\; +\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; \backslash ,\; \backslash \; Delta\; z\_\; \{i\})\}$

, где функции $E\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\}$и $cov\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{cov\}\}$соответственно определены в уравнениях (1) и (2) ниже и эквивалентны традиционным определениям выборочного среднего и ковариации ; однако они не предназначены для статистической оценки характеристик населения. В частности, уравнение Прайса является детерминированным уравнением разности, которое моделирует траекторию фактического среднего значения характеристики вдоль потока фактической популяции людей. Предполагая, что средняя пригодность $w\; \{\backslash \; displaystyle\; w\}$не равна нулю, часто полезно записать его как

$\Delta \; z\; =\; 1\; w\; cov\; \; (wi,\; zi)\; +\; 1\; w\; E\; \; (wi\; \Delta \; zi)\; \{\backslash \; displaystyle\; \backslash \; Delta\; \{z\}\; =\; \{\backslash \; frac\; \{1\}\; \{w\}\}\; \backslash \; operatorname\; \{cov\}\; (w\_\; \{i\},\; z\_\; \{i\})\; +\; \{\backslash \; frac\; \{1\}\; \{\; w\}\}\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; \backslash ,\; \backslash \; Delta\; z\_\; \{i\})\}$

В конкретном случае эта характеристика $zi\; =\; wi\; \{\backslash \; displaystyle\; z\_\; \{i\}\; =\; w\_\; \{i\}\; \}$(т.е. пригодность сама по себе является интересующей характеристикой), тогда уравнение Прайса переформулирует фундаментальную теорему Фишера о естественном отборе.

Чтобы доказать уравнение Прайса, необходимы следующие определения. Если $ni\; \{\backslash \; displaystyle\; n\_\; \{i\}\}$- это количество вхождений пары действительных чисел $xi\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$и $yi\; \{\backslash \; displaystyle\; y\_\; \{i\}\}$, затем:

• Среднее значение $xi\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$составляет:

$E\; \; (xi)\; =\; def\; 1\; \sum \; ini\; \sum \; ixini\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; (x\_\; \{i\})\; \backslash ;\; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{=\}\}\; \backslash ;\; \{\backslash \; frac\; \{1\; \}\; \{\backslash \; sum\; \_\; \{i\}\; n\_\; \{i\}\}\}\; \backslash \; sum\; \_\; \{i\}\; x\_\; \{i\}\; n\_\; \{i\}\}$

$(1)\; \{\backslash \; displaystyle\; (1)\}$

• Ковариация между $значения\; xi\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$и $yi\; \{\backslash \; displaystyle\; y\_\; \{i\}\}$:

$cov\; \; (xi,\; yi)\; =\; def\; 1\; \sum \; ini\; \sum \; ini\; [xi\; -\; E\; \; (xi)]\; [yi\; -\; E\; \; (yi)]\; =\; E\; \; (xiyi)\; -\; E\; \; (xi)\; E\; \; (yi)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{cov\}\; (\; x\_\; \{i\},\; y\_\; \{i\})\; \backslash ;\; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{=\}\}\; \backslash ;\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sum\; \_\; \{i\}\; n\_\; \{i\}\}\}\; \backslash \; sum\; \_\; \{i\}\; n\_\; \{i\}\; [x\_\; \{i\}\; -\; \backslash \; operatorname\; \{E\}\; (x\_\; \{i\})]\; [y\_\; \{i\}\; -\; \backslash \; operatorname\; \{E\}\; (y\_\; \{i\})]\; =\; \backslash \; operatorname\; \{E\}\; (\; x\_\; \{i\}\; y\_\; \{i\})\; -\; \backslash \; operatorname\; \{E\}\; (x\_\; \{i\})\; \backslash \; operatorname\; \{E\}\; (y\; \_\; \{i\})\}$

$(2)\; \{\backslash \; displaystyle\; (2)\}$

Обозначение $⟨xi⟩\; =\; E\; \; (xi)\; \{\backslash \; displaystyle\; \backslash \; langle\; x\_\; \{i\}\; \backslash \; rangle\; =\; \backslash \; operatorname\; \{E\}\; (x\_\; \{i\})\}$также будет использоваться, когда это удобно.

Предположим, существует популяция организмов, все из которых имеют генетические характеристики, описываемые некоторым действительным числом. Например, высокие значения числа представляют повышенную остроту зрения по сравнению с каким-либо другим организмом с более низким значением характеристики. В совокупности могут быть определены группы, для которых характерно одно и то же значение характеристики. Пусть индекс $i\; \{\backslash \; displaystyle\; i\}$идентифицирует группу с характеристикой $zi\; \{\backslash \; displaystyle\; z\_\; \{i\}\}$и пусть $ni\; \{\backslash \; displaystyle\; n\_\; \{i\}\}$- количество организмов в этой группе. Общее количество организмов тогда $n\; \{\backslash \; displaystyle\; n\}$, где:

$n\; =\; \sum \; ini\; \{\backslash \; displaystyle\; n\; =\; \backslash \; sum\; \_\; \{i\}\; n\_\; \{i\}\}$

Среднее значение характеристики $z\; \{\backslash \; displaystyle\; z\}$определяется как:

$z\; =\; def\; E\; \; (zi)\; =\; 1\; n\; \sum \; izini\; \{\backslash \; displaystyle\; z\; \backslash ;\; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{=\}\}\; \backslash ;\; \backslash \; operatorname\; \{E\}\; (z\_\; \{i\})\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; sum\; \_\; \{i\}\; z\_\; \{i\}\; n\_\; \{i\}\}$

$(3)\; \{\backslash \; displaystyle\; (3)\}$

Теперь предположим, что популяция воспроизводится и количество особей в группе $i\; \{\backslash \; displaystyle\; i\}$в следующем поколении представлено Автор $ni\; \prime \; \{\backslash \; displaystyle\; n\; \text{'}\_\; \{i\}\}$. Так называемый фитнес $wi\; \{\backslash \; displaystyle\; w\_\; \{i\}\}$группы $i\; \{\backslash \; displaystyle\; i\}$определяется как отношение количества его особей в следующем поколении к числу его особей в предыдущем поколении. То есть

$wi\; =\; ni\; \prime \; ni\; \{\backslash \; displaystyle\; w\_\; \{i\}\; =\; \{\backslash \; frac\; \{n\_\; \{i\}\; \text{'}\}\; \{n\_\; \{i\}\}\}\}$

$(4)\; \{\backslash \; displaystyle\; (4)\; \backslash ,\}$

Таким образом, утверждение, что группа «более приспособлена», равносильно утверждению, что ее члены производят больше потомства на каждого человека в следующем поколении. Точно так же $n\; \prime \; \{\backslash \; displaystyle\; n\; \text{'}\}$представляет общее количество людей во всех группах, которое может быть выражено как:

$n\; \prime \; =\; \sum \; ini\; \prime \; \{\backslash \; displaystyle\; n\text{'}\; =\; \backslash \; sum\; \_\; \{i\}\; n\; \text{'}\_\; \{i\}\}$

Кроме того, можно показать, что средняя приспособленность населения является темпом роста населения в целом, как в:

$w\; =\; def\; E\; E\; (wi)\; знак\; равно\; 1\; N\; \sum \; iwini\; =\; 1\; N\; \sum \; ini\; \prime \; nini\; =\; 1\; n\; \sum \; ini\; \prime \; =\; n\; \prime \; n\; \{\backslash \; displaystyle\; w\; \backslash ;\; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{=\}\}\; \backslash ;\; \backslash \; Operatorname\; \{\; E\}\; (w\_\; \{i\})\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; sum\; \_\; \{i\}\; w\_\; \{i\}\; n\_\; \{i\}\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; sum\; \_\; \{i\}\; \{\backslash \; frac\; \{n\_\; \{i\}\; \text{'}\}\; \{n\_\; \{i\}\}\}\; n\_\; \{i\}\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; sum\; \_\; \{i\}\; n\_\; \{i\}\text{'}\; =\; \{\backslash \; frac\; \{n\; \text{'}\; \}\; \{n\}\}\}$

$(5)\; \{\backslash \; displaystyle\; (5)\}$

Хотя общая численность населения может расти, доля людей из определенной группы может изменяться. В частности, если одна группа имеет более высокую приспособленность, чем другая группа, то группа с более высокой приспособленностью будет иметь большее увеличение представленности в следующем поколении, чем группа с более низкой приспособленностью. Средняя приспособленность показывает, как растет популяция, и группы с приспособленностью ниже среднего будут иметь тенденцию к пропорциональному снижению, в то время как группы с приспособленностью выше среднего будут иметь тенденцию к пропорциональному увеличению.

Наряду с изменением доли особей в каждой группе с течением времени, значения признаков в одной группе могут незначительно отличаться от поколения к поколению (например, из-за мутации ). Эти два давления вместе приведут к изменению среднего значения характеристики для всей популяции с течением времени. Предполагая, что значение $zi\; \prime \; \{\backslash \; displaystyle\; z\; \text{'}\_\; \{i\}\}$изменилось на точно такую ​​же величину для всех членов исходной группы, в новом поколении группы среднее значение $z\; \prime \; \{\backslash \; displaystyle\; z\; \text{'}\}$характеристики:

$z\; \prime \; =\; 1\; n\; \prime \; \sum \; izi\; \prime \; ni\; \prime \; \{\backslash \; displaystyle\; z\text{'}\; =\; \{\backslash \; frac\; \{1\}\; \{\; n\; \text{'}\}\}\; \backslash \; sum\; \_\; \{i\}\; z\text{'}\; \_\; \{i\}\; n\_\; \{i\}\; \text{'}\}$

$(6)\; \{\backslash \; displaystyle\; (6)\}$

где $zi\; \prime \; \{\backslash \; displaystyle\; z\text{'}\_\; \{i\}\}$- (возможно, новые) значения характеристики в группе $i\; \{\backslash \; displaystyle\; i\}$. Уравнение (2) показывает, что:

$cov\; \; (wi,\; zi)\; =\; E\; \; (wizi)\; -\; wz\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{cov\}\; (w\_\; \{i\},\; z\_\; \{i\})\; =\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; z\_\; \{i\})\; -\; wz\}$

$(7)\; \{\backslash \; displaystyle\; (7)\}$

Вызов изменения значения характеристики от родительской популяции к дочерней $\Delta \; zi\; \{\backslash \; displaystyle\; \backslash \; Delta\; z\_\; \{i\}\}$так, чтобы $\Delta \; zi\; =\; zi\; \prime \; -\; zi\; \{\backslash \; displaystyle\; \backslash \; Delta\; z\_\; \{i\}\; =\; z\; \text{'}\_\; \{i\}\; -z\_\; \{i\}\}$. Как видно из уравнения (1), оператор ожидаемого значения $E\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\}$имеет значение linear, поэтому

$E\; \; (wi\; \Delta \; zi)\; =\; E\; \; (wizi\; \prime )\; -\; E\; \; (wizi)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; \backslash ,\; \backslash \; Delta\; z\_\; \{i\})\; =\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; z\text{'}\_\; \{i\})\; -\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; z\_\; \{i\})\}$

$(8)\; \{\backslash \; displaystyle\; (8)\}$

Объединение уравнений (7) и (8) приводит к

$cov\; \; (wi,\; zi)\; +\; E\; \; (wi\; \Delta \; zi)\; =\; [E\; \; (wizi)\; -\; wz]\; +\; [E\; \; (wizi\; \prime )\; -\; E\; \; (wizi)]\; =\; E\; \; (wizi\; \prime )\; -\; wz\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{cov\}\; (w\_\; \{i\},\; z\_\; \{i\})\; +\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; \backslash ,\; \backslash \; Delta\; z\_\; \{i\})\; =\; \backslash \; left\; [\backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; z\_\; \{i\})\; -\; wz\; \backslash \; right]\; +\; \backslash \; left\; [\backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; z\; \text{'}\_\; \{i\})\; -\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; z\_\; \{i\})\; \backslash \; right]\; =\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; z\; \text{'}\_\; \{i\})\; -\; wz\}$

$(9)\; \{\backslash \; displaystyle\; (9)\}$

Теперь давайте вычислим первый член в равенстве над. Из уравнения (1) мы знаем, что:

$E\; \; (wizi\; \prime )\; =\; 1\; n\; \sum \; iwizi\; \prime \; ni\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; z\; \text{'}\_\; \{i\})\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; sum\; \_\; \{i\}\; w\_\; \{i\}\; z\; \text{'}\_\; \{i\}\; n\_\; \{i\}\}$

Подставляя определение пригодности, $wi\; =\; ni\; \prime \; ni\; \{\backslash \; textstyle\; w\_\; \{\; i\}\; =\; \{\backslash \; frac\; \{n\; \text{'}\_\; \{i\}\}\; \{n\_\; \{i\}\}\}\}$(Уравнение (4)), получаем:

$E\; \; (wizi\; \prime )\; =\; 1\; n\; \sum \; ini\; \prime \; nizi\; \prime \; ni\; =\; 1\; n\; \sum \; ini\; \prime \; zi\; \prime \; =\; n\; \prime \; n\; 1\; n\; \prime \; \sum \; izi\; \prime \; ni\; \prime \; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; z\; \text{'}\_\; \{i\})\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; sum\; \_\; \{i\}\; \{\backslash \; frac\; \{n\; \text{'}\_\; \{i\}\}\; \{n\_\; \{i\}\}\}\; z\text{'}\; \_\; \{i\}\; n\_\; \{i\}\; =\; \{\backslash \; frac\; \{1\}\; \{n\; \}\}\; \backslash \; sum\; \_\; \{i\}\; n\; \text{'}\_\; \{i\}\; z\text{'}\; \_\; \{i\}\; =\; \{\backslash \; frac\; \{n\; \text{'}\}\; \{n\}\}\; ~\; \{\backslash \; frac\; \{1\}\; \{n\text{'}\}\}\; \backslash \; sum\; \_\; \{i\}\; z\; \text{'}\_\; \{i\}\; n\text{'}\; \_\; \{i\}\}$

$(10)\; \{\backslash \; displaystyle\; (10)\}$

Затем, подставляя определения средней пригодности ($w\; =\; n\; \prime \; n\; \{\backslash \; textstyle\; w\; =\; \{\backslash \; frac\; \{n\; \text{'}\}\; \{n\}\}\}$) из уравнения (5) и средние дочерние характеристики ($z\; \prime \; \{\backslash \; textstyle\; z\text{'}\}$) из Уравнение (6) дает уравнение Прайса:

$cov\; \; (wi,\; zi)\; +\; E\; \; (wi\; \Delta \; zi)\; =\; wz\; \prime \; -\; wz\; =\; w\; \Delta \; z\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{cov\}\; (w\_\; \{i\},\; z\_\; \{i\})\; +\; \backslash \; operatorname\; \{E\}\; (w\_\; \{i\}\; \backslash ,\; \backslash \; Delta\; z\_\; \{i\})\; =\; wz\text{'}-wz\; =\; w\; \backslash ,\; \backslash \; Delta\; z\; \backslash ,\}$

Получение уравнение цены с непрерывным временем

Рассмотрим набор групп с $i\; =\; 1,...,\; n\; \{\backslash \; displaystyle\; i\; =\; 1,...,\; n\}$, которые характеризуются определенной чертой, обозначаемой $x\; i\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$. Число $ni\; \{\backslash \; displaystyle\; n\_\; \{i\}\}$лиц, принадлежащих к группе $i\; \{\backslash \; displaystyle\; i\}$, испытывает экспоненциальный рост:

$dnidt\; =\; fini\; \{\backslash \; displaystyle\; \{dn\_\; \{i\}\; \backslash \; over\; \{dt\}\}\; =\; f\_\; \{i\}\; n\_\; \{i\}\}$, где $fi\; \{\backslash \; displaystyle\; f\_\; \{i\}\}$соответствует пригодности группы. Мы хотим вывести уравнение, описывающее эволюцию ожидаемого значения признака во времени: $E\; (x)\; =\; \sum \; ipixi\; \equiv \; \mu ,\; pi\; =\; ni\; \sum \; jnj\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{E\}\; (x)\; =\; \backslash \; сумма\; \_\; \{i\}\; p\_\; \{i\}\; x\_\; \{i\}\; \backslash \; Equiv\; \backslash \; mu,\; \backslash \; quad\; p\_\; \{i\}\; =\; \{n\_\; \{i\}\; \backslash \; over\; \{\backslash \; sum\; \_\; \{j\}\; n\_\; \{j\}\}\}\}$На основе по цепному правилу мы можем вывести обыкновенное дифференциальное уравнение :$d\; \mu \; dt\; =\; \sum \; i\; \partial \; \mu \; \partial \; pidpidt\; +\; \sum \; i\; \partial \; \mu \; \partial \; xidxidt\; =\; \sum \; ixidpidt\; +\; \sum \; ipidxidt\; =\; \sum \; ixidpidt\; +\; E\; (dxdt)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{d\; \backslash \; mu\; \backslash \; over\; \{dt\}\}\; =\; \backslash \; sum\; \_\; \{i\}\; \{\backslash \; partial\; \backslash \; mu\; \backslash \; over\; \{\backslash \; partial\; p\_\; \{i\}\}\}\; \{dp\_\; \{i\}\; \backslash \; over\; \{dt\}\}\; +\; \backslash \; sum\; \_\; \{i\}\; \{\backslash \; partial\; \backslash \; mu\; \backslash \; over\; \{\backslash \; partial\; x\_\; \{i\}\}\}\; \{dx\_\; \{i\}\; \backslash \; over\; \{dt\}\}\; \backslash \backslash \; =\; \backslash \; sum\; \_\; \{i\}\; x\_\; \{i\}\; \{dp\_\; \{i\}\; \backslash \; over\; \{dt\}\}\; +\; \backslash \; sum\; \_\; \{i\}\; p\_\; \{i\}\; \{dx\_\; \{i\}\; \backslash \; over\; \{dt\}\}\; \backslash \backslash \; =\; \backslash \; sum\; \_\; \{i\}\; x\_\; \{i\}\; \{dp\_\; \{i\}\; \backslash \; over\; \{dt\}\}\; +\; \backslash \; mathbb\; \{E\}\; \backslash \; left\; (\{dx\; \backslash \; over\; \{dt\}\}\; \backslash \; right)\; \backslash \; end\; \{align\}\}\}$Дальнейшее применение цепное правило для $dpi\; /\; dt\; \{\backslash \; displaystyle\; dp\_\; \{i\}\; /\; dt\}$дает нам: $dpidt\; =\; \sum \; j\; \partial \; pi\; \partial \; njdnjdt,\; \partial \; pi\; \partial \; nj\; =\; \{-\; пи\; /\; N,\; я\; \ne \; J\; (1\; -\; пи)\; /\; N,\; я\; =\; J\; \{\backslash \; displaystyle\; \{dp\_\; \{i\}\; \backslash \; over\; \{dt\}\}\; =\; \backslash \; sum\; \_\; \{j\}\; \{\backslash \; partial\; p\_\; \{i\}\; \backslash \; over\; \{\backslash \; partial\; n\_\; \{j\}\}\}\; \{dn\_\; \{j\}\; \backslash \; over\; \{dt\}\},\; \backslash \; quad\; \{\backslash \; partial\; p\_\; \{i\}\; \backslash \; over\; \{\backslash \; partial\; n\_\; \{j\}\}\}\; =\; \{\backslash \; begin\; \{cases\}\; -p\_\; \{i\}\; /\; N,\; \backslash \; quad\; i\; \backslash \; neq\; j\; \backslash \backslash \; (1-p\_\; \{i\})\; /\; N,\; \backslash \; quad\; i\; =\; j\; \backslash \; end\; \{cases\}\}\}$Суммирование компонентов дает нам следующее: $dpidt\; =\; pi\; (fi\; -\; \sum \; jpjfj)\; =\; pi\; [fi\; -\; E\; (f)]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{dp\_\; \{i\}\; \backslash \; over\; \{dt\}\}\; =\; p\_\; \{i\}\; \backslash \; left\; (f\_\; \{i\}\; -\; \backslash \; sum\; \_\; \{j\}\; p\_\; \{j\}\; f\_\; \{j\}\; \backslash \; right)\; \backslash \backslash \; =\; p\_\; \{i\}\; \backslash \; left\; [f\_\; \{i\}\; -\; \backslash \; mathbb\; \{E\}\; (f)\; \backslash \; right]\; \backslash \; end\; \{выровнено\}\}\}$

, которое также известно как уравнение репликатора. Теперь обратите внимание, что:

$\sum \; ixidpidt\; =\; \sum \; ipixi\; [fi\; -\; E\; (f)]\; =\; E\; \{xi\; [fi\; -\; E\; (f)]\}\; =\; Cov\; (x,\; f)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; sum\; \_\; \{i\}\; x\_\; \{i\}\; \{dp\_\; \{i\}\; \backslash \; over\; \{dt\}\}\; =\; \backslash \; sum\; \_\; \{i\}\; p\_\; \{i\}\; x\_\; \{i\}\; \backslash \; left\; [f\_\; \{i\}\; -\; \backslash \; mathbb\; \{E\}\; (е)\; \backslash \; право]\; \backslash \backslash \; =\; \backslash \; mathbb\; \{E\}\; \backslash \; left\; \backslash \; \{x\_\; \{i\}\; \backslash \; left\; [f\_\; \{i\}\; -\; \backslash \; mathbb\; \{E\}\; (f)\; \backslash \; right]\; \backslash \; right\; \backslash \}\; \backslash \backslash \; =\; \{\backslash \; text\; \{Cov\}\}\; (x,\; f)\; \backslash \; end\; \{align\}\}\}$Следовательно, сложив все эти компоненты вместе, мы приходим к уравнению цены в непрерывном времени: $ddt\; E\; (x)\; =\; Cov\; (x,\; f)\; ⏟\; Эффект\; выбора\; +\; E\; (x\; \dot{})\; ⏟\; Динамический\; эффект\; \{\backslash \; displaystyle\; \{d\; \backslash \; over\; \{dt\}\}\; \backslash \; mathbb\; \{E\}\; (x)\; =\; \backslash \; underbrace\; \{\{\backslash \; text\; \{Cov\}\}\; (x,\; f)\}\; \_\; \{\backslash \; text\; \{Эффект\; выделения\}\}\; +\; \backslash \; underbrace\; \{\backslash \; mathbb\; \{E\}\; (\{\backslash \; dot\; \{x\}\})\}\; \_\; \{\backslash \; text\; \{Динамический\; эффект\}\}\}$

Когда значения характеристик $zi\; \{\backslash \; displaystyle\; z\_\; \{i\}\}$не изменяются от родительского к дочернему поколению, второй член в уравнении Прайса становится нулевым, что приводит к упрощенному версия уравнения Прайса:

$w\; \Delta \; z\; =\; cov\; \; (wi,\; zi)\; \{\backslash \; displaystyle\; w\; \backslash ,\; \backslash \; Delta\; z\; =\; \backslash \; operatorname\; \{cov\}\; \backslash \; left\; (w\_\; \{i\},\; z\_\; \{i\}\; \backslash \; right)\}$

, который можно переформулировать как:

$\Delta \; z\; =\; cov\; \; (vi,\; zi)\; \{\backslash \; displaystyle\; \backslash \; Delta\; z\; =\; \backslash \; operatorname\; \{cov\}\; \backslash \; left\; (v\_\; \{i\},\; z\_\; \{i\}\; \backslash \; right)\}$

где $vi\; \{\backslash \; displaystyle\; v\_\; \{i\}\}$- дробная пригодность: $vi\; =\; wi\; /\; w\; \{\backslash \; displaystyle\; v\_\; \{i\}\; =\; w\_\; \{i\}\; /\; w\}$.

Это простое уравнение Прайса можно доказать, используя определение в уравнении (2) над. Он делает следующее фундаментальное утверждение об эволюции: «Если определенная наследуемая характеристика коррелирует с увеличением дробной приспособленности, среднее значение этой характеристики в детской популяции будет выше, чем в родительской популяции».

Приложения

Уравнение Прайса может описывать любую систему, которая меняется со временем, но чаще всего применяется в эволюционной биологии. Развитие зрения представляет собой пример простого выбора направления. Развитие серповидноклеточной анемии показывает, как преимущество гетерозигот может повлиять на эволюцию признака. Уравнение Прайса также может применяться к признакам, зависящим от контекста населения, таким как эволюция соотношения полов. Кроме того, уравнение Прайса достаточно гибкое, чтобы моделировать черты второго порядка, такие как эволюция изменчивости. Уравнение Прайса также обеспечивает расширение эффекта Основателя, который показывает изменение популяционных характеристик в разных поселениях

Динамическая достаточность и простое уравнение Прайса

Иногда используемая генетическая модель кодирует достаточно информации в параметры используется уравнением цены, чтобы позволить вычислить параметры для всех последующих поколений. Это свойство называется динамической достаточностью. Для простоты нижеследующее рассматривает динамическую достаточность для простого уравнения цены, но также справедливо для полного уравнения цены.

Ссылаясь на определение в уравнении (2), можно записать простое уравнение цены для символа $z\; \{\backslash \; displaystyle\; z\}$:

$w\; (z\; \prime \; -\; z)\; =\; ⟨wizi⟩\; -\; wz\; \{\backslash \; displaystyle\; w\; (z\text{'}-z)\; =\; \backslash \; langle\; w\_\; \{i\}\; z\_\; \{i\}\; \backslash \; rangle\; -wz\}$

Для второго поколения:

$w\; \prime \; (z\; ″\; -\; z\; \prime )\; знак\; равно\; ⟨wi\; \prime \; zi\; \prime ⟩\; -\; w\; \prime \; z\; \prime \; \{\backslash \; displaystyle\; w\; \text{'}(z\text{'}\; \text{'}-\; z\text{'})\; =\; \backslash \; langle\; w\; \text{'}\_\; \{i\}\; z\text{'}\; \_\; \{i\}\; \backslash \; rangle\; -w\text{'}z\; \text{'}\}$

Простое уравнение цены для $z\; \{\backslash \; displaystyle\; z\}$дает только значение $z\; \prime \; \{\backslash \; displaystyle\; z\text{'}\}$для первое поколение, но не дает нам значения $w\; \prime \; \{\backslash \; displaystyle\; w\; \text{'}\}$и $⟨wizi⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; w\_\; \{i\}\; z\_\; \{i\}\; \backslash \; rangle\; \}$, которые необходимы для вычисления $z\; ″\; \{\backslash \; displaystyle\; z\; \text{'}\text{'}\}$для второго поколения. Переменные $wi\; \{\backslash \; displaystyle\; w\_\; \{i\}\}$и $⟨wizi⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; w\_\; \{i\}\; z\_\; \{i\}\; \backslash \; rangle\}$могут обе можно рассматривать как характеристики первого поколения, поэтому уравнение Прайса также можно использовать для их расчета:

$w\; (w\; \prime \; -\; w)\; =\; ⟨wi\; 2⟩\; -\; w\; 2\; w\; (⟨wi\; \prime \; zi\; \prime ⟩\; -\; ⟨wizi⟩)\; =\; ⟨wi\; 2\; zi⟩\; -\; w\; ⟨wizi⟩\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; w\; (w\text{'}-w)\; =\; \backslash \; langle\; w\_\; \{i\}\; ^\; \{2\}\; \backslash \; rangle\; -w\; ^\; \{\; 2\}\; \backslash \backslash \; w\; \backslash \; left\; (\backslash \; langle\; w\; \text{'}\_\; \{i\}\; z\text{'}\; \_\; \{i\}\; \backslash \; rangle\; -\; \backslash \; langle\; w\_\; \{i\}\; z\_\; \{i\}\; \backslash \; rangle\; \backslash \; right)\; =\; \backslash \; langle\; w\_\; \{i\}\; ^\; \{\; 2\}\; z\_\; \{i\}\; \backslash \; rangle\; -w\; \backslash \; langle\; w\_\; \{i\}\; z\_\; \{i\}\; \backslash \; rangle\; \backslash \; end\; \{align\}\}\}$

Пять переменных нулевого поколения $w\; \{\backslash \; displaystyle\; w\}$, $z\; \{\backslash \; displaystyle\; z\}$, $⟨wizi⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; w\_\; \{i\}\; z\_\; \{i\}\; \backslash \; rangle\}$, $⟨wi\; 2⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; w\_\; \{i\}\; ^\; \{2\}\; \backslash \; rangle\; \}$и $⟨wi\; 2\; zi\; \{\backslash \; displaystyle\; \backslash \; langle\; w\_\; \{i\}\; ^\; \{2\}\; z\_\; \{i\}\}$должны быть известны, прежде чем приступать к вычислению первых трех переменные генерации $w\; \prime \; \{\backslash \; displaystyle\; w\; \text{'}\}$, $z\; \prime \; \{\backslash \; displaystyle\; z\; \text{'}\}$и $⟨wi\; \prime \; zi\; \prime ⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; w\text{'}\; \_\; \{i\}\; z\; \text{'}\_\; \{i\}\; \backslash \; rangle\}$, которые необходимы для вычисления $z\; ″\; \{\backslash \; displaystyle\; z\; \text{'}\text{'}\}$для второго поколения. Можно видеть, что в целом уравнение Прайса нельзя использовать для распространения вперед во времени, если нет способа вычисления высших моментов $⟨win⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; w\_\; \{i\}\; ^\; \{n\}\; \backslash \; rangle\}$и $⟨winzi⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; w\_\; \{i\}\; ^\; \{n\}\; z\_\; \{i\}\; \backslash \; rangle\}$из нижних моментов, независимо от поколение. Динамическая достаточность означает, что такие уравнения могут быть найдены в генетической модели, что позволяет использовать уравнение Прайса отдельно в качестве пропагатора динамики модели вперед во времени.

Простое уравнение цены было основано на предположении, что символы $zi\; \{\backslash \; displaystyle\; z\_\; \{i\}\}$не заменяют единицу поколение. Если предполагается, что они меняются, а $z\; i\; \{\backslash \; displaystyle\; z\_\; \{i\}\}$является значением символа в дочерней совокупности, тогда необходимо использовать полное уравнение Прайса. Смена характера может происходить разными способами. Следующие два примера иллюстрируют две такие возможности, каждая из которых позволяет по-новому взглянуть на уравнение цены.

Соответствие генотипа

Мы сосредотачиваемся на идее соответствия генотипа. Индекс $i\; \{\backslash \; displaystyle\; i\}$указывает генотип, а количество генотипов типа $i\; \{\backslash \; displaystyle\; i\}$в детской популяции:

$ni\; \prime \; =\; \sum \; jwjinj\; \{\backslash \; displaystyle\; n\; \text{'}\_\; \{i\}\; =\; \backslash \; sum\; \_\; \{j\}\; w\_\; \{ji\}\; n\_\; \{j\}\; \backslash ,\}$

, что дает пригодность:

$wi\; =\; ni\; \prime \; ni\; \{\backslash \; displaystyle\; w\_\; \{i\}\; =\; \{\backslash \; frac\; \{n\; \text{'}\_\; \{i\}\}\; \{n\_\; \{i\}\}\}\}$

Поскольку индивидуальная изменчивость $zi\; \{\backslash \; displaystyle\; z\_\; \{i\}\}$делает без изменений, средняя изменчивость будет:

$z\; =\; 1\; n\; \sum \; iziniz\; \prime \; =\; 1\; n\; \prime \; \sum \; izini\; \prime \; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; z\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; sum\; \_\; \{i\}\; z\_\; \{i\}\; n\_\; \{i\}\; \backslash \backslash \; z\; \text{'}=\; \{\backslash \; frac\; \{1\}\; \{n\text{'}\}\}\; \backslash \; sum\; \_\; \{i\}\; z\_\; \{i\}\; n\; \text{'}\_\; \{i\}\; \backslash \; end\; \{выровнено\}\}\; \}$

с этими определениями теперь применяется простое уравнение цены.

Пригодность по происхождению

В данном случае мы хотим рассмотреть идею о том, что приспособленность измеряется количеством детей в организме, независимо от их генотипа. Обратите внимание, что теперь у нас есть два метода группировки: по происхождению и по генотипу. Именно это усложнение потребует полного уравнения цены. Количество детей у организма типа $i\; \{\backslash \; displaystyle\; i\}$:

$ni\; \prime \; =\; ni\; \sum \; jwij\; \{\backslash \; displaystyle\; n\; \text{'}\_\; \{i\}\; =\; n\_\; \{i\}\; \backslash \; сумма\; \_\; \{j\}\; w\_\; \{ij\}\; \backslash ,\}$

, которая дает пригодность:

$wi\; =\; ni\; \prime \; ni\; =\; \sum \; jwij\; \{\backslash \; displaystyle\; w\_\; \{i\}\; =\; \{\backslash \; frac\; \{n\; \text{'}\_\; \{i\}\}\; \{\; n\_\; \{i\}\}\}\; =\; \backslash \; sum\; \_\; \{j\}\; w\_\; \{ij\}\}$

Теперь у нас есть символы в дочерней совокупности, которые являются средними символами $i\; \{\backslash \; displaystyle\; i\}$-й родитель.

$zj\; \prime \; =\; \sum \; iniziwij\; \sum \; iniwij\; \{\backslash \; displaystyle\; z\; \text{'}\_\; \{j\}\; =\; \{\backslash \; frac\; \{\backslash \; sum\; \_\; \{i\}\; n\_\; \{i\}\; z\_\; \{i\}\; w\_\; \{ij\}\}\; \{\backslash \; sum\; \_\; \{i\}\; n\_\; \{i\}\; w\_\; \{ij\}\}\}\}$

с глобальными символами:

$z\; =\; 1\; n\; \sum \; iziniz\; \prime \; =\; 1\; n\; \prime \; \sum \; izini\; \prime \; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; z\; =\; \{\backslash \; frac\; \{\; 1\}\; \{n\}\}\; \backslash \; sum\; \_\; \{i\}\; z\_\; \{i\}\; n\_\; \{i\}\; \backslash \backslash \; z\; \text{'}=\; \{\backslash \; frac\; \{1\}\; \{n\text{'}\}\}\; \backslash \; sum\; \_\; \{i\}\; z\_\; \{i\}\; n\text{'}\_\; \{i\}\; \backslash \; end\; \{align\}\}\}$

с этими определениями теперь применяется полное ценовое уравнение.

Использование изменения средней характеристики ($z\; \prime \; -\; z\; \{\backslash \; displaystyle\; z\text{'}-z\}$) для каждого поколения в качестве меры эволюционный прогресс не всегда уместен. Могут быть случаи, когда среднее значение остается неизменным (и ковариация между приспособленностью и характеристикой равна нулю), в то время как эволюция, тем не менее, продолжается.

Критическое обсуждение использования уравнения Прайса можно найти у van Veelen (2005), van Veelen et al. (2012) и ван Веелен (2020). Франк (2012) обсуждает критику van Veelen et al. (2012).

Уравнение Прайса присутствует в сюжете и названии триллера 2008 года WΔZ.

Уравнение Прайса также присутствует на плакатах в компьютерной игре BioShock 2, в котором потребитель тоника "Brain Boost" выводит уравнение цены, одновременно читая книгу. Действие игры разворачивается в 1950-х годах, значительно раньше, чем работа Прайса.

• Примеры уравнения цены