Доля населения

редактировать

A Доля населения, обычно обозначается $P {\ displaystyle P}$ $P$ или Греческая буква $π {\ displaystyle \ pi}$ $\ pi$ - это параметр, который описывает процентное значение, связанное с генеральной совокупностью. Например, Перепись США 2010 года показала, что 83,7% американского населения были идентифицированы как не латиноамериканцы или латиноамериканцы. Значение 0,837 - это доля населения. В целом, доля населения и другие параметры популяции неизвестны. перепись может быть проведена для определения фактического значения параметра численности населения, но часто перепись нецелесообразна из-за ее затрат и затрат времени.

Доля населения обычно оценивается с помощью несмещенной выборочной статистики, полученной в ходе наблюдательного исследования или эксперимента. Например, Национальная конференция по технологической грамотности провела национальный опрос 2000 взрослых, чтобы определить процент экономически неграмотных взрослых. Исследование показало, что 72% из 2000 отобранных взрослых не понимают, что такое валовой внутренний продукт. Значение 72% - это примерная пропорция. Образец пропорции обычно обозначается $p ^ {\ displaystyle {\ hat {p}}}$ ${\ hat {p}}$ , а в некоторых учебниках - $p {\ displaystyle p}$ $p$ .

Contents

1 Математическое определение
2 Оценка
- 2.1 Доказательство
- 2.2 Условия для вывода
- 2.3 Пример
  - 2.3.1 Решение
- 2.4 Значение параметра в доверительном интервале
- 2.5 Общее ошибки и неверные интерпретации оценки
3 См. также
4 Ссылки

Математическое определение

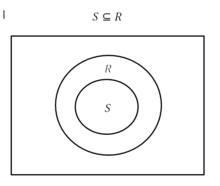
Иллюстрация диаграммы Венна набора

R {\ displaystyle R}

R

и его подмножества

S {\ Displaystyle S}

S

. Долю можно рассчитать, измерив, сколько из

S {\ displaystyle S}

S

находится в

R {\ displaystyle R}

R

A пропорция математически определяется как отношение значений в подмножестве $S {\ displaystyle S}$ $S$ до значений в наборе $R {\ displaystyle R}$ $R$ .

Таким образом, долю населения можно определить следующим образом :

$P = XN {\ displaystyle P = {\ frac {X} {N}}}$ ${\ displaystyle P = {\ frac {X} { N}}}$ (где $X {\ displaystyle X}$ $X$ - количество успехов в генеральной совокупности, и $N {\ displaystyle N}$ $N$ - размер совокупности)

Это математическое определение можно обобщить, чтобы обеспечить определение доли выборки:

$p ^ = xn {\ displaystyle {\ hat {p}} = {\ frac {x} {n}}}$ ${\ displaystyle {\ hat {p}} = {\ frac {x} {n}}}$ (где $x {\ displaystyle x}$ $x$ - количество успехов в выборке, а $n {\ displaystyle n}$ $n$ - размер выборки, полученной из генеральной совокупности)

Оценка

Одним из основных направлений исследований вывести Общая статистика определяет «истинное» значение параметра. Как правило, фактическое значение параметра никогда не будет найдено, если только не будет проведена перепись изучаемого населения. Однако существуют статистические методы, которые можно использовать для получения разумной оценки параметра. Эти методы включают доверительные интервалы и проверку гипотез.

Оценка стоимости доли населения может иметь большое значение в областях сельского хозяйства, бизнеса, экономика, образование, инженерия, экология, медицина, право, политология, психология и социология.

Доля населения может быть оценена с помощью доверительного интервала, известного как доля одной выборки в Z-интервал, формула которого приведена ниже:

$p ^ ± z ∗ p ^ (1 - p ^) n {\ displaystyle {\ hat {p}} \ pm z ^ {*} {\ sqrt {\ frac {{\ hat {p}} (1 - {\ hat {p}})} {n}}}}$ ${\ displaystyl e {\ hat {p}} \ pm z ^ {*} {\ sqrt {\ frac {{\ hat {p}} (1 - {\ hat {p}})} {n}}}}$ (где $p ^ {\ displaystyle {\ hat {p }}}$ ${\ hat {p}}$ - пропорция выборки, $n {\ displaystyle n}$ $n$ - размер выборки, а $z ∗ {\ displaystyle z ^ {*}}$ $z ^ {*}$ - верхнее $1 - C 2 {\ displaystyle {\ frac {1-C} {2}}}$ ${\ displaystyle {\ frac {1- C} {2}}}$ критическое значение стандартного стандартного дистрибутива ution для уровня достоверности $C {\ displaystyle C}$ ${\ displaystyle C}$ )

Proof

Чтобы вывести формулу для доли одной выборки в Z-интервале, необходимо учитывать распределение выборки пропорций выборки. Среднее значение выборочного распределения пропорций выборки обычно обозначается как $μ p ^ = P {\ displaystyle \ mu _ {\ hat {p}} = P}$ ${\ displaystyle \ mu _ {\ hat {p}} = P}$ , а его стандартное отклонение обозначается как $σ p ^ = P (1 - P) n {\ displaystyle \ sigma _ {\ hat {p}} = {\ sqrt {\ frac {P (1-P)} {n}}}}$ ${\ displaystyle \ sigma _ {\ hat {p}} = {\ sqrt {\ frac {P (1-P)} {п }}}}$ . Поскольку значение $P {\ displaystyle P}$ $P$ неизвестно, будет использоваться несмещенная статистика $p ^ {\ displaystyle {\ hat {p}}}$ ${\ hat {p}}$ для $P {\ displaystyle P}$ $P$ . Среднее значение и стандартное отклонение переписываются как $μ p ^ = p ^ {\ displaystyle \ mu _ {\ hat {p}} = {\ hat {p}}}$ ${\ displaystyle \ mu _ {\ hat {p }} = {\ hat {p}}}$ и $σ p ^ = p ^ (1 - p ^) n {\ displaystyle \ sigma _ {\ hat {p}} = {\ sqrt {\ frac {{\ hat {p}} (1 - {\ hat {p}}))} {n}}}}$ ${\ displaystyle \ sigma _ {\ hat {p}} = {\ sqrt {\ frac {{\ шляпа {p}} (1 - {\ hat {p}})} {n}}}}$ соответственно. Ссылаясь на центральную предельную теорему , выборочное распределение пропорций выборки приблизительно нормальное - при условии, что выборка достаточно велика и не перекручена.

Предположим, вычислена следующая вероятность: $P (- z ∗ < p ^ − P p ^ ( 1 − p ^) n < z ∗) = C {\displaystyle P(-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}$ ${\ displaystyle P (-z ^ {*} <{\ frac {{\ hat {p }} - P} {\ sqrt {\ frac {{\ hat {p}} (1 - {\ hat {p}})} {n}}}} <z ^ {*}) = C}$ , где $0 < C < 1 {\displaystyle 0$ ${\ displaystyle 0 <C <1}$ и $± z ∗ {\ displaystyle \ pm z ^ {*}}$ ${\ displaystyle \ pm z ^ {*}}$ - стандартные критические значения.

Выборочное распределение пропорций образца приблизительно нормально, когда оно удовлетворяет требованиям Центральной предельной теоремы.

Неравенство $- z ∗ < p ^ − P p ^ ( 1 − p ^) n < z ∗ {\displaystyle -z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}$ ${\ displaystyle -z ^ {*} <{\ frac {{\ hat {p}} - P} {\ sqrt {\ frac {{\ hat {p}} (1 - {\ hat {p}})} {n}}}} <z ^ {*}}$ можно алгебраически переписать следующим образом:

$- z ∗ < p ^ − P p ^ ( 1 − p ^) n < z ∗ ⇒ − z ∗ p ^ ( 1 − p ^) n < p ^ − P < z ∗ p ^ ( 1 − p ^) n ⇒ − p ^ − z ∗ p ^ ( 1 − p ^) n < − P < − p ^ + z ∗ p ^ ( 1 − p ^) n ⇒ p ^ − z ∗ p ^ ( 1 − p ^) n < P < p ^ + z ∗ p ^ ( 1 − p ^) n {\displaystyle -z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}} Из алгебраической работы, проделанной выше, это очевидно с уровня достоверности C {\ displaystyle C}$ $C$ , что $P {\ displaystyle P}$ $P$ может находиться между значениями $p ^ ± z ∗ p ^ (1 - p ^) n {\ displaystyle {\ hat { p}} \ pm z ^ {*} {\ sqrt {\ frac {{\ hat {p}} (1 - {\ hat {p}})} {n}}}}$ ${\ displaystyl e {\ hat {p}} \ pm z ^ {*} {\ sqrt {\ frac {{\ hat {p}} (1 - {\ hat {p}})} {n}}}}$ .

Условия вывода

Как правило, формула, используемая для оценки доли населения, требует подстановки известных числовых значений. Однако эти числовые значения нельзя подставлять в формулу «вслепую», поскольку статистический вывод r требует, чтобы оценка неизвестного параметра была обоснованной. Чтобы оценка параметра была обоснованной, необходимо проверить три условия:

Индивидуальное наблюдение данных должно быть получено из простой случайной выборки из представляющей интерес совокупности.
Отдельные наблюдения данных должны отображать нормальность. Это можно проверить математически с помощью следующего определения:
- Пусть $n {\ displaystyle n}$ $n$ будет размером данной случайной выборки, и пусть $p ^ {\ displaystyle {\ hat {p}}}$ ${\ hat {p}}$ - пропорция выборки. Если $np ^ ≥ 10 {\ displaystyle n {\ hat {p}} \ geq 10}$ ${\ displaystyle n {\ hat {p}} \ geq 10}$ и $n (1 - p ^) ≥ 10 {\ displaystyle n (1- { \ hat {p}}) \ geq 10}$ ${\ displaystyle n (1 - {\ hat {p}}) \ geq 10}$ , то отдельные наблюдения данных отображают нормальность.
Отдельные наблюдения данных должны быть независимыми друг от друга. Это можно проверить математически с помощью следующего определения:
- Пусть $N {\ displaystyle N}$ $N$ будет размером исследуемой совокупности, и пусть $n {\ displaystyle n }$ $n$ быть размером простой случайной выборки генеральной совокупности. Если $N ≥ 10 n {\ displaystyle N \ geq 10n}$ ${\ displaystyle N \ geq 10n}$ , то отдельные наблюдения данных не зависят друг от друга.

Иногда упоминаются условия для SRS, нормальности и независимости в качестве условий для инструмента вывода в большинстве статистических учебников.

Пример

Предположим, что президентские выборы проходят в условиях демократии. Случайная выборка из 400 имеющих право голоса избирателей среди демократических избирателей показывает, что 272 избирателя поддерживают кандидата B. Политолог хочет определить, какой процент избирателей поддерживает кандидата B.

Чтобы ответить на вопрос политолога, a Одновыборочная пропорция в Z-интервале с уровнем достоверности 95% может быть построена для определения доли правомочных избирателей в этой демократии, которые поддерживают кандидата Б.

Решение

Из случайной выборки известно, что $p ^ = 272 400 = 0,68 {\ displaystyle {\ hat {p}} = {\ frac {272} {400}} = 0,68}$ ${\ displaystyle {\ hat {p}} = {\ frac {272} {400}} = 0,68}$ с выборкой размер $n = 400 {\ displaystyle n = 400}$ ${\ displaystyle n = 400}$ . Перед построением доверительного интервала будут проверены условия вывода.

Поскольку случайная выборка из 400 избирателей была получена из голосующих, условие для простой случайной выборки было выполнено.
Пусть $n = 400 {\ displaystyle n = 400}$ ${\ displaystyle n = 400}$ и $p ^ = 0,68 {\ displaystyle {\ hat {p}} = 0,68}$ ${\ displaystyle {\ hat {p}} = 0,68}$ , будет проверяться, $np ^ ≥ 10 {\ displaystyle n {\ шляпа {p}} \ geq 10}$ ${\ displaystyle n {\ hat {p}} \ geq 10}$ и $n (1 - p ^) ≥ 10 {\ displaystyle n (1 - {\ hat {p}}) \ geq 10}$ ${\ displaystyle n (1 - {\ hat {p}}) \ geq 10}$

(400) (0,68) ≥ 10 ⇒ 272 ≥ 10 {\ displaystyle (400) (0,68) \ geq 10 \ Rightarrow 272 \ geq 10}

{\ displaystyle (400) (0,68) \ geq 10 \ Rightarrow 272 \ geq 10}

(400) (1–0,68) ≥ 10 ⇒ 128 ≥ 10 {\ displaystyle (400) (1-0,68) \ geq 10 \ Rightarrow 128 \ geq 10}

{\ displaystyle (400) (1-0.68) \ geq 10 \ Rightarrow 128 \ geq 10}

Выполнено условие нормальности.

Пусть $N {\ displaystyle N}$ $N$ будет численностью избирателей в этой демократии, и пусть $n = 400 {\ displaystyle n = 400}$ ${\ displaystyle n = 400}$ . Если $N ≥ 10 n {\ displaystyle N \ geq 10n}$ ${\ displaystyle N \ geq 10n}$ , тогда существует независимость.

N ≥ 10 (400) ⇒ N ≥ 4000 {\ displaystyle N \ geq 10 (400) \ Rightarrow N \ geq 4000}

{\ displaystyle N \ geq 10 (400) \ Rightarrow N \ geq 4000}

Можно предположить, что численность населения

N {\ displaystyle N}

N

для избирателей этой демократии составляет не менее 4000. Следовательно, условие независимости выполнено.

После проверки условий вывода допустимо построить доверительный интервал.

Пусть $p ^ = 0,68, n = 400, {\ displaystyle {\ hat {p}} = 0,68, n = 400,}$ ${\ displaystyle {\ hat {p}} = 0,68, n = 400,}$ и $C = 0,95. {\ displaystyle C = 0,95}$ ${\ displaystyle C = 0,95}$

Чтобы найти для $z ∗ {\ displaystyle z ^ {*}}$ $z ^ {*}$ , выражение $1 - C 2 { Используется \ displaystyle {\ frac {1-C} {2}}}$ ${\ displaystyle {\ frac {1- C} {2}}}$ .

$1 - C 2 = 1 - 0,95 2 = 0,05 2 = 0,0250 {\ displaystyle {\ frac {1-C} {2}} = {\ frac {1-0,95} {2}} = {\ frac { 0,05} {2}} = 0,0250}$ ${\ displaystyle {\ frac {1-C} {2}} = {\ frac {1-0.95} {2}} = {\ гидроразрыв {0,05} {2}} = 0,0250}$

Стандартная нормальная кривая с

z ∗ {\ displaystyle z ^ {*}}

z ^ {*}

, что дает площадь верхнего хвоста 0,0250 и площадь 0,9750 для

Z ≤ z ∗ {\ displaystyle Z \ leq z ^ {*}}

{\ displaystyle Z \ leq z ^ {*}}

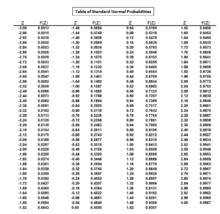
Таблица со стандартными нормальными вероятностями для

Z ≤ z {\ displaystyle Z \ leq z}

{\ displaystyle Z \ leq z}

путем изучения стандартная нормальная колоколообразная кривая, значение для $z ∗ {\ displaystyle z ^ {*}}$ $z ^ {*}$ может быть определено путем определения того, какой стандартный балл дает стандартной нормальной кривой площадь верхнего хвоста 0,0250 или площадь из 1 - 0,0250 = 0,9750. Значение для $z ∗ {\ displaystyle z ^ {*}}$ $z ^ {*}$ также можно найти с помощью таблицы стандартных нормальных вероятностей.

Из таблицы стандартных нормальных вероятностей значение $Z {\ displaystyle Z}$ $Z$ , которое дает площадь 0,9750, составляет 1,96. Следовательно, значение для $z ∗ {\ displaystyle z ^ {*}}$ $z ^ {*}$ равно 1,96.

Значения для $p ^ = 0,68 {\ displaystyle {\ hat {p}} = 0,68}$ ${\ displaystyle {\ hat {p}} = 0,68}$ , $n = 400 {\ displaystyle n = 400}$ ${\ displaystyle n = 400}$ , $z ∗ = 1,96 { \ displaystyle z ^ {*} = 1.96}$ ${\ displaystyle z ^ {*} = 1,96}$ теперь можно подставить в формулу для одновыборочной пропорции в интервале Z:

$p ^ ± z ∗ p ^ (1 - p ^) п ⇒ (0,68) ± (1,96) (0,68) (1–0,68) (400) ⇒ 0,68 ± 1,96 0,000544 {\ displaystyle {\ hat {p}} \ pm z ^ {*} {\ sqrt {\ frac {{ \ hat {p}} (1 - {\ hat {p}})} {n}}} \ Rightarrow (0,68) \ pm (1,96) {\ sqrt {\ frac {(0,68) (1-0,68)} { (400)}}} \ Rightarrow 0,68 \ pm 1,96 {\ sqrt {0,000544}}}$ ${\ displaystyle {\ hat {p}} \ pm z ^ {*} {\ sqrt {\ frac {{\ hat {p}} (1 - {\ hat {p}) })} {n}}} \ Rightarrow (0,68) \ pm (1,96) {\ sqrt {\ frac {(0,68) (1-0,68)} {(400)}}} \ Rightarrow 0,68 \ pm 1,96 {\ sqrt {0.000544}}}$ $⇒ (0,63429, 0,72571) {\ displaystyle \ Rightarrow {\ bigl (} 0,63429,0,72571 {\ bigr)}}$ ${\ displaystyle \ Rightarrow {\ bigl (} 0,63429,0.72571 {\ bigr)}}$

Основываясь на условиях вывода и формуле для доли одной выборки в интервале Z, с уровнем достоверности 95% можно сделать вывод, что процент населения избирателя в этой демократии, поддерживающего кандидата B, составляет от 63,429% до 72,571%.

Значение параметра в диапазоне доверительного интервала

Часто задаваемый вопрос в выводной статистике: включен ли параметр в доверительный интервал. Единственный способ ответить на этот вопрос - провести перепись. Ссылаясь на пример, приведенный выше, вероятность того, что доля населения находится в диапазоне доверительного интервала, равна либо 1, либо 0. То есть, параметр включен в диапазон интервала или нет. Основная цель доверительного интервала - лучше проиллюстрировать, каким может быть идеальное значение параметра.

Распространенные ошибки и неверные интерпретации оценки

Очень распространенной ошибкой, возникающей при построении доверительного интервала, является убеждение в том, что уровень достоверности, например $C = 95% { \ displaystyle C = 95 \%}$ ${\ displaystyle C = 95 \%}$ , означает вероятность 95%. Это неверно. Уровень уверенности основан на степени достоверности, а не вероятности. Следовательно, значения $C {\ displaystyle C}$ $C$ находятся исключительно между 0 и 1.

См. Также

Литература