Фазовый портрет

Геометрическое представление Потенциальная энергия и фазовый портрет простого маятника. Обратите внимание, что ось x, будучи угловой, оборачивается сама на себя через каждые 2π радиан. 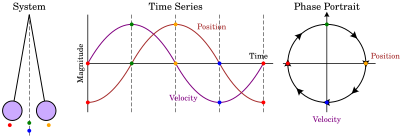Иллюстрация того, как будет построен фазовый портрет для движения простого маятник. 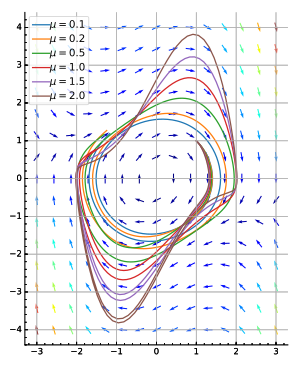Фазовый портрет уравнения Ван дер Поля, $d\; 2\; ydt\; 2\; +\; \mu \; (y\; 2\; -\; 1)\; dydt\; +\; y\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\; \}\; y\}\; \{dt\; ^\; \{2\}\}\}\; +\; \backslash \; mu\; (y\; ^\; \{2\}\; -1)\; \{\backslash \; frac\; \{dy\}\; \{dt\}\}\; +\; y\; =\; 0\}$.

A фазовый портрет - геометрическое представление траекторий динамической системы в фазовой плоскости. Каждый набор начальных условий представлен разными c призывать или указывать.

Фазовые портреты - бесценный инструмент в изучении динамических систем. Они состоят из графика типичных траекторий в пространстве состояний. Это раскрывает такую ​​информацию, как наличие аттрактора, репеллера или предельного цикла для выбранного значения параметра. Концепция топологической эквивалентности важна для классификации поведения систем, определяя, когда два разных фазовых портрета представляют одно и то же качественное динамическое поведение. Аттрактор - это стабильная точка, которую еще называют «стоком». Репеллер считается нестабильной точкой, которая также известна как «источник».

График фазового портрета динамической системы изображает траектории системы (со стрелками) и устойчивые установившиеся состояния (с точками) и нестабильные установившиеся состояния (с кружками) в пространстве состояний. Оси представляют собой переменные состояния.

• 1 Примеры
• 2-фазные портреты для визуализации поведения систем обыкновенных дифференциальных уравнений
• 3 См. Также
• 4 Ссылки
• 5 Внешние ссылки

• Простой маятник, см. Рисунок (справа).
• Простой гармонический осциллятор, в котором фазовый портрет состоит из эллипсов с центром в начале координат, который является фиксированной точкой.
• Ван дер Генератор Pol см. Рисунок (внизу справа).
• Плоскость параметров (c-плоскость) и Набор Мандельброта

Фазовый портрет представляет собой направленное поведение системы ODE. Фазовый портрет может свидетельствовать об устойчивости системы.

Стабильность

Нестабильность	Большинство решений системы имеют тенденцию к ∞ с течением времени
Асимптотически стабильные	Все решения системы со временем стремятся к нулю
Нейтрально стабильны	Ни одно из решений системы не стремится к ∞ с течением времени, но большинство решений не стремятся ни к 0

Поведение фазового портрета системы ОДУ может быть определено собственными значениями или следом и определителем ( трассировка = λ 1 + λ 2, определитель = λ 1 x λ 2) системы.

Поведение фазового портрета

Собственное значение, След, Детерминант	Форма фазового портрета
λ1λ 2 действительны и имеют противоположный знак; Определитель < 0	Седло (нестабильно)
λ1λ 2 действительны и одного знака, а λ 1 ≠ λ 2; 0 < determinant < (trace / 4)	Узел (стабильно, если трассировка < 0, unstable if trace>0)
λ1λ 2 имеют как действительную, так и мнимую составляющие; 0 < (trace / 4) < determinant	Спираль (стабильная, если след < 0, unstable if trace>0)

• Фазовое пространство
• Фазовая плоскость

1. ^ Хейнс Миллер и Артур Маттак. 18.03 Дифференциальные уравнения. Весна 2010 г. Массачусетский технологический институт: MIT OpenCourseWare, https://ocw.mit.edu. Лицензия: Creative Commons BY-NC-SA. (Дополнительные примечания 26 Хейнса Миллера: https://ocw.mit.edu/courses/mat Mathematics/18-03-differential-equations-spring-2010/readings/supp_notes/MIT18_03S10_chapter_26.pdf)

• Jordan, D.W.; Смит, П. (2007). Нелинейные обыкновенные дифференциальные уравнения (четвертое изд.). Издательство Оксфордского университета. ISBN 978-0-19-920824-1. Глава 1.
• Стивен Строгац (2001). Нелинейная динамика и хаос: с приложениями к физике, биологии, химии и технике. ISBN 9780738204536.

• Linear Phase Portraits, Mathlet.