Ориентированный матроид

редактировать

Теория ориентированного матроида допускает комбинаторный подход к теореме о максимальном потоке и минимальном разрезе. Сеть со значением потока, равным пропускной способности отрезка

ориентированный матроид - это математическая структура, которая абстрагирует свойства ориентированные графы, векторные расположения над упорядоченными полями и расположения гиперплоскостей над упорядоченными полями. Для сравнения, обычный (т.е. неориентированный) матроид абстрагирует свойства зависимости, которые являются общими как для графов, которые не обязательно направлены, так и для расположение векторов над полями , которые не обязательно упорядочены.

Все ориентированные матроиды имеют лежащий в основе матроид. Таким образом, результаты об обычных матроидах могут быть применены к ориентированным матроидам. Однако обратное ложно; некоторые матроиды не могут стать ориентированным матроидом, ориентируя нижележащую структуру (например, схемы или независимые наборы). Различие между матроидами и ориентированными матроидами обсуждается ниже.

Матроиды часто используются в таких областях, как теория размерностей и алгоритмы. Поскольку ориентированный матроид включает дополнительные сведения об ориентированной природе структуры, его полезность распространяется на несколько областей, включая геометрию и оптимизацию.

Содержание

1 Предпосылки
2 Аксиоматизации
- 2.1 Аксиомы схемы
- 2.2 Векторные аксиомы
- 2.3 Аксиомы хиротопов
- 2.4 Эквивалентность
3 Примеры
- 3.1 Направленные графы
- 3.2 Линейная алгебра
- 3.3 Расположение гиперплоскостей
- 3.4 Выпуклый многогранник
4 Результаты
- 4.1 Ориентируемость
- 4.2 Двойственность
- 4.3 Топологическое представление
- 4.4 Геометрия
- 4.5 Оптимизация
5 Ссылки
6 Дополнительная литература
- 6.1 Книги
- 6.2 Статьи
- 6.3 В сети
7 Внешние ссылки

Предпосылки

Чтобы абстрагироваться от концепции ориентации на краях графа для множеств необходимо уметь задавать «направление» элементам множества. Это достигается с помощью следующего определения наборов со знаком.

Набор со знаком, $X {\ displaystyle X}$ $X$ , объединяет набор объектов $X _ {\ displaystyle {\ underline {X}}}$ $\ underline {X}$ с разделением этого набора на два подмножества: $X + {\ displaystyle X ^ {+}}$ $X^+$ и $X - {\ displaystyle X ^ {-}}$ $X^-$ .

Члены

X + {\ displaystyle X ^ {+}}

X^+

называются положительными элементами; элементы

X - {\ displaystyle X ^ {-}}

X^-

являются отрицательными элементами.

Множество $X _ = X + ∪ X - {\ displaystyle {\ underline { X}} = X ^ {+} \ cup X ^ {-}}$ $\ underline {X} = X ^ + \ cup X ^ -$ называется поддержкой $X {\ displaystyle X}$ $X$ .
пустого набора со знаком, $∅ { \ displaystyle \ emptyset}$ $\ empty$ , определяется как пустой набор $∅ _ {\ displaystyle {\ underline {\ emptyset}}}$ ${\ displaystyle {\ underline {\ emptyset}}}$ в сочетании с его «разделением» на два пустых набора: $∅ + {\ displaystyle \ emptyset ^ {+}}$ ${\ displaystyle \ emptyset ^ {+}}$ и $∅ - {\ displaystyle \ emptyset ^ {-}}$ ${\ displaystyle \ emptyset ^ {-}}$ .
подписанный набор $Y {\ displaystyle Y}$ $Y$ является противоположностью $X {\ displaystyle X}$ $X$ , т. Е. $Y = - X {\ displaystyle Y = -X}$ $Y = -X$ , если и только если $Y + = X - {\ displaystyle Y ^ {+} = X ^ {-}}$ $Y ^ + = X ^ -$ и $Y - = X + {\ displaystyle Y ^ {-} = X ^ {+}}$ $Y ^ - = X ^ +$

Учитывая элемент опоры $x {\ displaystyle x}$ $x$ , мы будем писать $x {\ displaystyle x}$ $x$ для положительного элемента и $- x {\ displaystyle -x}$ $-x$ fo r отрицательный элемент. Таким образом, подписанный набор просто добавляет отрицательные знаки к выделенным элементам. Это будет иметь смысл как «направление» только тогда, когда мы будем рассматривать ориентацию более крупных структур. Тогда знак каждого элемента будет кодировать его направление относительно этой ориентации.

Аксиоматизация

Как и обычные матроиды, существует несколько эквивалентных систем аксиом. (Такие структуры, которые обладают множеством эквивалентных аксиоматизаций, называются криптоморфными.)

Аксиомы схемы

Пусть $E {\ displaystyle E}$ $E$ будет любой набор. Мы называем $E {\ displaystyle E}$ $E$ базовым набором. Пусть $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ будет набором наборов со знаком, каждый из которых поддерживается подмножеством $E {\ displaystyle E}$ $E$ . Если следующие аксиомы верны для $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ , то эквивалентно $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ - это набор схем со знаком для ориентированного матроида на $E {\ displaystyle E}$ $E$ .

(C0) $∅ ∉ C {\ displaystyle \ emptyset \ notin {\ mathcal {C}}}$ $\ empty \ notin \ mathcal {C}$
(C1) (симметричный) $Для всех X ∈ C, - X ∈ C. {\ displaystyle {\ text {For all}} X \ in {\ mathcal {C}}, ~ - \! X \ in {\ mathcal {C}}.}$ ${\ displaystyle {\ text {For all}} X \ in { \ mathcal {C}}, ~ - \! X \ in {\ mathcal {C}}.}$
(C2) (несравнимо) $Для всех X, Y ∈ C, если X _ ⊆ Y _, то (X = Y или X = - Y). {\ displaystyle {\ text {For all}} X, Y \ in {\ mathcal {C}}, ~~ {\ text {if}} {\ underline {X}} \ substeq {\ underline {Y}} { \ text {then}} (X = Y {\ text {или}} X = -Y).}$ ${\ displaystyle {\ text {For all}} X, Y \ in {\ mathcal {C}}, ~~ {\ text {if}} {\ underline {X}} \ substeq {\ underline {Y}} {\ text {then}} (X = Y {\ text {или}} X = -Y).}$
(C3) (слабое исключение) Для всех X, Y ∈ C, X ≠ - Y с e ∈ X + ∩ Y - существует Z ∈ C такое, что {\ displaystyle {\ text {For all}} X, Y \ in {\ mathcal {C}}, X \ neq -Y {\ text {с an}} e \ in X ^ {+} \ cap Y ^ {-} {\ text {есть}} Z \ in {\ mathcal {C}} {\ text {такое, что}}}
- $Z + ⊆ (Икс + ∪ Y +) ∖ {e} и {\ displaystyle Z ^ {+} \ substeq (X ^ {+} \ cup Y ^ {+}) \ setminus \ {e \} {\ text {и }}}$ ${\ displaystyle Z ^ {+} \ substeq (X ^ {+} \ cup Y ^ {+}) \ setminus \ {e \} {\ text {and}}}$
- $Z - ⊆ (X - ∪ Y -) ∖ {e}. {\ displaystyle Z ^ {-} \ substeq (X ^ {-} \ cup Y ^ {-}) \ setminus \ {e \}.}$ $Z ^ - \ substeq (X ^ - \ cup Y ^ -) \ setminus \ {е \}.$

Аксиомы вектора

Состав наборов со знаком $X {\ displaystyle X}$ $X$ и $Y {\ displaystyle Y}$ $Y$ - это набор со знаком $X ∘ Y {\ displaystyle X \ circ Y}$ ${\ displaystyle X \ circ Y}$ определяется как $Икс ∘ Y _ = X _ ∪ Y _ {\ displaystyle {\ underline {X \ circ Y}} = {\ underline {X}} \ cup {\ underline {Y}}}$ ${\ displaystyle {\ underline {X \ circ Y}} = {\ underline {X} } \ cup {\ underline {Y}}}$ , $(Икс ∘ Y) + знак равно Икс + ∪ (Y + ∖ Икс -) {\ displaystyle (X \ circ Y) ^ {+} = X ^ {+} \ cup \ left (Y ^ {+} \ setminus X ^ {-} \ right)}$ ${\ displaystyle (X \ circ Y) ^ {+} = X ^ {+} \ cup \ left (Y ^ {+} \ setminus X ^ {-} \ справа)}$ и $(X ∘ Y) - = X - ∪ (Y - ∖ X +) {\ displaystyle (X \ circ Y) ^ {- } = X ^ {-} \ cup \ left (Y ^ {-} \ setminus X ^ {+} \ right)}$ ${\ displaystyle (X \ circ Y) ^ {-} = X ^ {-} \ cup \ left (Y ^ {- } \ setminus X ^ {+} \ right)}$ . Векторы ориентированного матроида представляют собой композиции схем. Векторы $V {\ displaystyle {\ mathcal {V}}}$ ${\ mathcal {V}}$ ориентированного матроида удовлетворяют следующим аксиомам:

$∅ ∈ V {\ displaystyle \ emptyset \ in {\ mathcal {V }}}$ ${\ displaystyle \ emptyset \ in {\ mathcal {V} }}$
$V = - V {\ displaystyle {\ mathcal {V}} = - {\ mathcal {V}}}$ ${\ displaystyle {\ mathcal {V}} = - {\ mathcal {V}}}$
для всех $X, Y ∈ V {\ displaystyle X, Y \ in {\ mathcal {V}}}$ ${\ displaystyle X, Y \ in {\ mathcal {V}}}$ , $Икс ∘ Y ∈ V {\ displaystyle X \ circ Y \ in {\ mathcal {V}}}$ ${\ displaystyle X \ circ Y \ in {\ mathcal {V}}}$
для всех X, Y ∈ V {\ displaystyle X, Y \ in {\ mathcal {V}}}, e ∈ X + ∩ Y - {\ displaystyle e \ in X ^ {+} \ cap Y ^ {-}}и е ∈ (Икс _ ∖ Y _) ∪ (Y _ ∖ X _) ∪ (X + ∩ Y +) ∪ (X - ∩ Y -) {\ displaystyle f \ in ({\ underline {X}} \ setminus {\ underline {Y}}) \ cup ({\ underline {Y}} \ setminus {\ underline {X}}) \ cup (X ^ {+} \ cap Y ^ {+}) \ cup (X ^ {-} \ cap Y ^ {-})}, существует Z ∈ V {\ displaystyle Z \ in {\ mathcal {V}}}, например что
- $Z + ⊂ X + ∪ Y + ∖ e {\ displaystyle Z ^ {+} \ subset X ^ {+} \ cup Y ^ {+} \ setminus e}$ ${\ displaystyle Z ^ {+} \ subset X ^ {+} \ cup Y ^ {+} \ setminus e}$ ,
- $Z - ⊂ X - ∪ Y - ∖ е {\ displaystyle Z ^ {-} \ subset X ^ {-} \ cup Y ^ {-} \ setminus e}$ ${\ displaystyle Z ^ {-} \ subset X ^ {-} \ чашка Y ^ {-} \ setminus e}$ и
- $f ∈ Z _ {\ displaystyle f \ in {\ underline {Z}}}$ ${\ displaystyle f \ in {\ underline {Z}}}$ .

Аксиомы хиротопа

Пусть $E {\ displaystyle E}$ $E$ будет таким, как указано выше. Для каждого неотрицательного целого числа $r {\ displaystyle r}$ $r$ хиротоп ранга $r {\ displaystyle r}$ $r$ является функцией $χ: E r → {- 1, 0, 1} {\ displaystyle \ chi \ двоеточие E ^ {r} \ to \ {- 1,0,1 \}}$ $\ chi \ двоеточие E ^ r \ to \ {- 1,0,1 \}$ , который удовлетворяет следующим аксиомам:

(B0) (нетривиально): $χ {\ displaystyle \ chi}$ $\ chi$ не равно нулю тождественно
(B1) (чередуется): для любой перестановки $σ {\ displaystyle \ sigma}$ $\ sigma$ и $x 1,…, xr ∈ E {\ displaystyle x_ {1}, \ dots, x_ {r} \ in E}$ $x_1, \ dots, x_r \ in E$ , $χ (Икс σ (1),…, Икс σ (г)) = sign ⁡ (σ) χ (x 1,…, xr) {\ Displaystyle \ чи \ влево (x _ {\ sigma (1)}, \ точки, x _ {\ sigma (r)} \ right) = \ operatorname {sgn} (\ sigma) \ chi \ left (x_ {1}, \ dots, x_ {r} \ right)}$ ${\ displaystyle \ chi \ left (x _ {\ sigma (1)}, \ dots, x _ {\ sigma (r)} \ right) = \ operatorname {sgn} (\ sigma) \ chi \ left (x_ {1}, \ dots, x_ {r} \ right)}$ , где $sgn ⁡ (σ) {\ displaystyle \ operatorname {sgn} (\ sigma)}$ $\ operatorname {sgn} (\ sigma)$ - знак перестановки.
(B2) (обмен): для любых $x 1,…, xr, y 1,…, yr ∈ E {\ displaystyle x_ {1}, \ dots, x_ {r}, y_ {1}, \ dots, y_ {r} \ in E}$ $x_1, \ dots, x_r, y_1, \ dots, y_r \ in E$ вс ch, что $χ (yi, x 2,…, xr) χ (y 1,…, yi - 1, x 1, yi + 1,…, yr) ≥ 0 {\ displaystyle \ chi (y_ {i}, x_ {2}, \ dots, x_ {r}) \ chi (y_ {1}, \ dots, y_ {i-1}, x_ {1}, y_ {i + 1}, \ dots, y_ {r }) \ geq 0}$ $\ chi (y_i, x_2, \ dots, x_r) \ chi (y_1, \ dots, y_ {i-1}, x_1, y_ {i + 1}, \ dots, y_r) \ ge 0$ для каждого $i {\ displaystyle i}$ $я$ , тогда у нас также есть $χ (x 1,…, xr) χ (y 1,…, Год) ≥ 0 {\ displaystyle \ chi \ left (x_ {1}, \ dots, x_ {r} \ right) \ chi \ left (y_ {1}, \ dots, y_ {r} \ right) \ geq 0}$ $\ chi \ left (x_1, \ dots, x_r \ right) \ chi \ left (y_1, \ dots, y_r \ right) \ ge0$ .

Термин хиротоп происходит от математического понятия хиральности, которое представляет собой понятие, абстрагированное от химия, где оно используется для различения молекул, имеющих одинаковые структура за исключением отражения.

Эквивалентность

Каждый хиротоп ранга $r {\ displaystyle r}$ $r$ порождает набор оснований матроида на $E {\ displaystyle E}$ $E$ состоящий из тех $r {\ displaystyle r}$ $r$ -element подмножеств, которым $χ {\ displaystyle \ chi}$ $\ chi$ присваивает ненулевое значение. После этого хиротоп может подписать цепи этого матроида. Если $C {\ displaystyle C}$ $C$ - схема описанного матроида, то $C ⊂ {x 1,…, xr, xr + 1} {\ displaystyle C \ subset \ { x_ {1}, \ dots, x_ {r}, x_ {r + 1} \}}$ $C \ subset \ {x_1, \ dots, x_r, x_ {r + 1} \}$ где ${x 1,…, xr} {\ displaystyle \ {x_ {1}, \ dots, x_ {r} \}}$ $\ {x_1, \ точки, x_r \}$ - это основа. Тогда $C {\ displaystyle C}$ $C$ может быть подписано положительными элементами

C + = {xi: (- 1) i χ (x 1,…, xi - 1, xi + 1,…, Xr + 1) = 1} {\ displaystyle C ^ {+} = \ {x_ {i}: (- 1) ^ {i} \ chi (x_ {1}, \ dots, x_ {i-1) }, x_ {i + 1}, \ dots, x_ {r + 1}) = 1 \}}

{\ displaystyle C ^ {+} = \ {x_ {i}: (- 1) ^ {i} \ chi (x_ {1 }, \ точки, x_ {i-1}, x_ {i + 1}, \ dots, x_ {r + 1}) = 1 \}}

и отрицательные элементы - дополнение. Таким образом, хиротоп порождает ориентированные основания ориентированного матроида. В этом смысле (B0) - непустая аксиома для базисов, а (B2) - свойство обмена базисами.

Примеры

Ориентированные матроиды часто вводятся (например, Бахема и Керна) как абстракция для ориентированных графов или систем линейных неравенств. Ниже приведены явные конструкции.

Направленные графы

Для орграфа мы определяем схему со знаком из стандартной схемы графа следующим способом. Поддержка схемы со знаком $X _ {\ displaystyle \ textstyle {\ underline {X}}}$ $\ textstyle \ underline {X}$ - стандартный набор ребер в минимальном цикле. Мы идем по циклу по часовой стрелке или против часовой стрелки, присваивая те ребра, ориентация которых совпадает с направлением, положительным элементам $X + {\ displaystyle \ textstyle X ^ {+}}$ $\ textstyle X ^ +$ и тем ребрам, у которых ориентация не соответствует направлению к отрицательным элементам $X - {\ displaystyle \ textstyle X ^ {-}}$ $\ textstyle X ^ -$ . Если $C {\ displaystyle \ textstyle {\ mathcal {C}}}$ $\ textstyle \ mathcal {C}$ - это набор всех таких $X {\ displaystyle \ textstyle X}$ $\ textstyle X$ , тогда $C {\ displaystyle \ textstyle {\ mathcal {C}}}$ $\ textstyle \ mathcal {C}$ - набор схем со знаком ориентированного матроида на множестве ребер ориентированного графа.

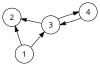
Ориентированный граф

Если мы рассмотрим ориентированный граф справа, то мы увидим, что есть только две схемы, а именно ${(1, 2), (1, 3), (3, 2)} {\ displaystyle \ textstyle \ {(1,2), (1,3), (3,2) \}}$ $\ textstyle \ {(1,2), (1,3), (3,2) \}$ и ${(3, 4), (4, 3)} {\ displaystyle \ textstyle \ {(3,4), (4,3) \}}$ $\ textstyle \ {(3,4), (4,3) \}$ . Тогда есть только четыре возможных схемы со знаком, соответствующих ориентации по часовой стрелке и против часовой стрелки, а именно ${(1, 2), - (1, 3), - (3, 2)} {\ displaystyle \ textstyle \ {(1, 2), - (1,3), - (3,2) \}}$ $\ textstyle \ {(1,2), - (1,3), - (3,2) \}$ , ${- (1, 2), (1, 3), (3, 2)} {\ displaystyle \ textstyle \ {- (1,2), (1,3), (3,2) \}}$ $\ textstyle \ {- (1,2), (1, 3), (3,2) \}$ , ${(3, 4), (4, 3)} {\ displaystyle \ textstyle \ {(3,4), ( 4,3) \}}$ $\ textstyle \ {(3,4), (4,3) \}$ и ${- (3, 4), - (4, 3)} {\ displaystyle \ textstyle \ {- (3,4), - (4, 3) \}}$ $\ textstyle \ {- (3,4), - (4,3) \}$ . Эти четыре набора образуют набор схем со знаком ориентированного матроида на множестве ${(1, 2), (1, 3), (3, 2), (3, 4), (4, 3)} {\ displaystyle \ textstyle \ {(1,2), (1,3), (3,2), (3,4), (4,3) \}}$ $\ textstyle \ {(1,2), (1,3), (3,2), (3,4), (4,3) \}$ .

Линейная алгебра

Если $E {\ displaystyle \ textstyle E}$ $\ textstyle E$ - любое конечное подмножество $R n {\ displaystyle \ textstyle \ mathbb {R} ^ {n}}$ $\ textstyle \ mathbb {R} ^ n$ , тогда набор минимальных линейно зависимых множеств образует набор схем матроида на $E {\ displaystyle \ textstyle E}$ $\ textstyle E$ . Чтобы распространить эту конструкцию на ориентированные матроиды, для каждой схемы ${v 1,…, vm} {\ displaystyle \ textstyle \ {v_ {1}, \ dots, v_ {m} \}}$ $\ textstyle \ {v_1, \ dots, v_m \}$ существует минимальная линейная зависимость

∑ i = 1 м λ ivi = 0 {\ displaystyle \ sum _ {i = 1} ^ {m} \ lambda _ {i} v_ {i} = 0}

\ сумма_ {я = 1} ^ м \ lambda_i v_i = 0

с $λ я ∈ R {\ displaystyle \ textstyle \ lambda _ {i} \ in \ mathbb {R}}$ $\ textstyle \ lambda_i \ in \ mathbb {R}$ . Тогда схема со знаком $X = {X +, X -} {\ displaystyle \ textstyle X = \ {X ^ {+}, X ^ {-} \}}$ $\ textstyle X = \ {X ^ +, X ^ - \}$ имеет положительные элементы $Икс + = {vi: λ я>0} {\ displaystyle \ textstyle X ^ {+} = \ {v_ {i}: \ lambda _ {i}>0 \}}$ $\textstyle X^+=\{v_i:\lambda_i>0 \}$ и отрицательные элементы $X - = {vi: λ i < 0 } {\displaystyle \textstyle X^{-}=\{v_{i}:\lambda _{i}<0\}}$ $\ textstyle X ^ - = \ {v_i: \ lambda_i <0 \}$ . Набор всех таких $X {\ displaystyle \ textstyle X}$ $\ textstyle X$ образует набор схем со знаком ориентированного матроида на $E {\ displaystyle \ textstyle E}$ $\ textstyle E$ . Ориентированные матроиды, которые могут быть реализованы таким образом, называются представляемыми.

Учитывая тот же набор векторов $E {\ displaystyle E}$ $E$ , мы можно определить тот же ориентированный матроид с хиротопом $χ: E r → {- 1, 0, 1} {\ displaystyle \ chi: E ^ {r} \ rightarrow \ {- 1,0,1 \}}$ $\ chi : E ^ r \ rightarrow \ {- 1,0,1 \}$ . Для любого $x 1,…, xr ∈ E {\ displaystyle x_ {1}, \ dots, x_ {r} \ in E}$ $x_1, \ dots, x_r \ in E$ пусть

χ ( x 1,…, xr) знак равно sgn ⁡ (det (x 1,…, xr)) {\ displaystyle \ chi (x_ {1}, \ dots, x_ {r}) = \ operatorname {sgn} (\ det (x_ {1}, \ точки, x_ {r}))}

{\ displaystyle \ chi (x_ {1}, \ dots, x_ {r}) = \ имя оператора {sgn} (\ det (x_ {1}, \ dots, x_ {r}))}

где правая часть уравнения является знаком детерминанта . Тогда $χ {\ displaystyle \ chi}$ $\ chi$ - хиротоп того же ориентированного матроида на множестве $E {\ displaystyle E}$ $E$ .

Расположение гиперплоскостей

Настоящее расположение гиперплоскостей $A = {H 1,…, H n} {\ displaystyle {\ mathcal {A}} = \ {H_ {1}, \ ldots, H_ {n} \}}$ ${\ displaystyle {\ mathcal {A}} = \ {H_ {1}, \ ldots, H_ {n} \}}$ - конечный набор гиперплоскостей в $R d {\ displaystyle \ mathbb {R} ^ {d}}$ ${\ displaystyle \ mathbb { R} ^ {d}}$ , каждая из которых содержит начало координат. Выбирая одну сторону каждой гиперплоскости в качестве положительной стороны, мы получаем расположение полупространств. Компоновка полупространства разбивает окружающее пространство на конечный набор ячеек, каждая из которых определяется тем, на какой стороне каждой гиперплоскости она приземляется. То есть присвоить каждой точке $x ∈ R d {\ displaystyle x \ in \ mathbb {R} ^ {d}}$ ${\ displaystyle x \ in \ mathbb {R} ^ {d}}$ подписанный набор $X = (X +, X -) {\ displaystyle X = (X ^ {+}, X ^ {-})}$ ${\ displaystyle X = (X ^ {+}, X ^ {-})}$ с $i ∈ X + {\ displaystyle i \ in X ^ {+}}$ ${\ displaystyle i \ in X ^ {+}}$ , если $x {\ displaystyle x}$ $x$ находится на положительной стороне $H i {\ displaystyle H_ {i}}$ $H_ {i}$ и $i ∈ X - {\ displaystyle i \ in X ^ {-}}$ ${\ displaystyle i \ in X ^ {-}}$ , если $x {\ displaystyle x}$ $x$ находится на отрицательной стороне $H i {\ displaystyle H_ {i}}$ $H_ {i}$ . Этот набор наборов со знаком определяет набор ковекторов ориентированного матроида, которые являются векторами дуально ориентированного матроида.

Выпуклый многогранник

Гюнтер М. Циглер вводит ориентированные матроиды через выпуклые многогранники.

Результаты

Ориентируемость

Стандартный матроид называется ориентируемым, если его схемы являются опорами схем со знаком некоторого ориентированного матроида. Известно, что все реальные представимые матроиды ориентируемы. Также известно, что класс ориентируемых матроидов замкнут относительно взятия миноров, однако список запрещенных миноров для ориентируемых матроидов, как известно, бесконечен. В этом смысле ориентированные матроиды представляют собой гораздо более строгую формализацию, чем обычные матроиды.

Двойственность

Подобно тому, как матроиды имеют уникальные дуальные, ориентированные матроиды имеют уникальные ортогональные двойники. Это означает, что лежащие в основе матроиды двойственны и что кокосхемы подписаны так, что они ортогональны каждой схеме. Два знаковых множества называются ортогональными, если пересечение их опор пусто или если ограничение их положительных элементов до пересечения и отрицательных элементов до пересечения образуют два неидентичных и несовпадающих знаковых множества. Существование и уникальность дуально ориентированного матроида зависит от того факта, что каждая знаковая схема ортогональна каждой знаковой кокцепи. Чтобы понять, почему ортогональность необходима для уникальности, достаточно взглянуть на приведенный выше пример орграфа. Мы знаем, что для плоских графов двойственный матроид схемы является матроидом схемы плоского дуального графа. Таким образом, существует столько же дуальных ориентированных матроидов, сколько способов ориентировать граф и его двойственные.

Чтобы увидеть явную конструкцию этого уникального ортогонального дуально ориентированного матроида, рассмотрим хиротоп $ориентированного матроида χ: E r → {- 1, 0, 1} {\ displaystyle \ chi: E ^ {r } \ rightarrow \ {- 1,0,1 \}}$ $\ chi : E ^ r \ rightarrow \ {- 1,0,1 \}$ . Если мы рассмотрим список элементов $x 1,…, xk ∈ E {\ displaystyle x_ {1}, \ dots, x_ {k} \ in E}$ $x_1, \ dots, x_k \ in E$ как циклическую перестановку, тогда мы определить $sgn ⁡ (x 1,…, xk) {\ displaystyle \ operatorname {sgn} (x_ {1}, \ dots, x_ {k})}$ ${\ displaystyle \ operatorname {sgn} (x_ {1}, \ dots, x_ {k})}$ как знак ассоциированного перестановка. Если $χ ∗: E | E | - r → {- 1, 0, 1} {\ displaystyle \ chi ^ {*}: E ^ {| E | -r} \ rightarrow \ {- 1,0,1 \}}$ $\ chi ^ *: E ^ {| E | -r} \ rightarrow \ {- 1,0,1 \}$ - это определяется как

χ ∗ (x 1,…, xr) ↦ χ (xr + 1,…, x | E |) sgn ⁡ (x 1,…, xr, xr + 1,…, x | E |), {\ displaystyle \ chi ^ {*} (x_ {1}, \ dots, x_ {r}) \ mapsto \ chi (x_ {r + 1}, \ dots, x_ {| E |}) \ operatorname {sgn } (x_ {1}, \ dots, x_ {r}, x_ {r + 1}, \ dots, x_ {| E |}),}

{\ displaystyle \ chi ^ {*} (x_ {1}, \ dots, x_ {r}) \ mapsto \ chi (x_ {r + 1}, \ dots, x_ {| E |}) \ operatorname {sgn} (x_ {1}, \ dots, x_ {r}, x_ {r + 1}, \ dots, x_ { | E |}),}

затем $χ ∗ {\ displaystyle \ chi ^ { *}}$ $\ chi ^ *$ - хиротоп уникального ортогонального дуально ориентированного матроида.

Топологическое представление

Это пример псевдолинейного расположения, которое отличается от любого расположение линий.

Не все ориентированные матроиды можно представить, то есть не все имеют реализации в виде точечных конфигураций или, что то же самое, расположения гиперплоскостей. Однако в некотором смысле все ориентированные матроиды близки к реализации в виде гиперплоскостей. В частности, теорема о топологическом представлении Фолкмана – Лоуренса утверждает, что любой ориентированный матроид имеет реализацию в виде конфигурации псевдосфер. A $d {\ displaystyle d}$ $d$ -мерная псевдосфера - это вложение $e: S d ↪ S d + 1 {\ displaystyle e: S ^ {d} \ hookrightarrow S ^ { d + 1}}$ $e: S ^ d \ hookrightarrow S ^ {d + 1}$ такой, что существует гомеоморфизм $h: S d + 1 → S d + 1 {\ displaystyle h: S ^ {d + 1} \ rightarrow S ^ {d + 1}}$ $h: S ^ {d + 1} \ rightarrow S ^ {d + 1}$ так, чтобы $h ∘ e {\ displaystyle h \ circ e}$ $h \ circ e$ вставлял $S d {\ displaystyle S ^ {d}}$ $S ^ {d}$ как экватор $S d + 1 {\ displaystyle S ^ {d + 1}}$ $S ^ { d + 1}$ . В этом смысле псевдосфера - это просто ручная сфера (в отличие от диких сфер ). Расположение псевдосферы в $S d {\ displaystyle S ^ {d}}$ $S ^ {d}$ представляет собой набор псевдосфер, пересекающихся по псевдосферам. Наконец, теорема о топологическом представлении Фолкмана Лоуренса утверждает, что каждый ориентированный матроид ранга $d + 1 {\ displaystyle d + 1}$ $d + 1$ может быть получен из расположения псевдосферы в $S d {\ displaystyle S ^ {d}}$ $S ^ {d}$ . Он назван в честь Джона Фолкмана и Джима Лоуренса, опубликовавших его в 1978 году.

Геометрия

Зонотоп, представляющий собой сумму отрезков Минковского, является фундаментальной моделью для ориентированных матроиды. Шестнадцать темно-красных точек (справа) образуют сумму Минковского четырех невыпуклых множеств (слева), каждое из которых состоит из пары красных точек. Их выпуклые корпуса (заштрихованные розовым цветом) содержат знаки плюса (+): правый знак плюс - это сумма левых знаков плюс.

Теория ориентированных матроидов повлияла на развитие комбинаторной геометрии, особенно теория выпуклых многогранников, зонотопов и конфигураций векторов (расположения гиперплоскостей ). Многие результаты - теорема Каратеодори, теорема Хелли, теорема Радона, теорема Хана – Банаха, теорема Крейна – Мильмана, лемма Фаркаша - может быть сформулирована с использованием соответствующих ориентированных матроидов.

Оптимизация

В выпуклой геометрии симплексный алгоритм линейного программирования интерпретируется как отслеживание пути вдоль вершины выпуклого многогранника. Теория ориентированных матроидов изучает комбинаторные инварианты, которые проявляются в знаковых паттернах матриц, которые появляются как основы обмена поворотных алгоритмов.

Разработка системы аксиом для ориентированных матроидов была инициирована Р. Тиррелл Рокафеллар для описания знаковых паттернов матриц, возникающих в результате операций поворота симплексного алгоритма Данцига; Рокафеллар был вдохновлен исследованиями Альберта В. Такера таких знаков в «Таблицах Такера».

Теория ориентированных матроидов привела к прорывам в комбинаторной оптимизации. В линейном программировании это был язык, на котором Роберт Г. Бланд сформулировал свое правило поворота, с помощью которого симплекс-алгоритм избегает циклов.. Точно так же его использовали Терлаки и Чжан, чтобы доказать, что их перекрестные алгоритмы имеют конечное завершение для задач линейного программирования. Аналогичные результаты были получены в выпуклом квадратичном программировании Тоддом и Терлаки. Он был применен к дробно-линейному программированию, задачам квадратичного программирования и задачам линейной дополнительности.

Вне комбинаторной оптимизации, теории ОМ также появляется в выпуклой минимизации в теории «монотропного программирования» Рокафеллара и связанных с ней понятиях «усиленного спуска». Точно так же теория матроидов повлияла на разработку комбинаторных алгоритмов, в частности, жадного алгоритма. В более общем смысле, гридоид полезен для изучения конечного завершения алгоритмов.

Ссылки

Дополнительная литература

Книги

Бахем, Ахим; Керн, Уолтер (1992). Двойственность линейного программирования: введение в ориентированные матроиды. Universitext. Springer-Verlag. DOI : 10.1007 / 978-3-642-58152-6. ISBN 978-3-540-55417-2. MR 1230380.
Бьёрнер, Андерс ; Лас Вергнас, Мишель ; Штурмфельс, Бернд ; Белый, Нил; Циглер, Гюнтер (1999). Ориентированные матроиды. Энциклопедия математики и ее приложений. 46 (2-е изд.). Издательство Кембриджского университета. ISBN 978-0-521-77750-6. Zbl 0944.52006.
Боковски, Юрген (2006). Вычислительно-ориентированные матроиды. Классы эквивалентности матриц в естественных рамках. Издательство Кембриджского университета. ISBN 978-0-521-84930-2. Zbl 1120.52011.
Лоулер, Юджин (2001). Комбинаторная оптимизация: сети и матроиды. Дувр. ISBN 978-0-486-41453-9. Zbl 1058.90057.
Эвар Д. Неринг и Альберт У. Такер, 1993, Линейные программы и связанные с ними проблемы, Academic Press. (элементарный)
Рокафеллар, Р. Тиррелл (1984). Сетевые потоки и монотропная оптимизация. Wiley-Interscience. переиздано Athena Scientific из Dimitri Bertsekas, 1998.
Ziegler, Günter M. (1994). Лекции по многогранникам. Нью-Йорк: Springer-Verlag.
Рихтер-Геберт, Юрген; Циглер, Гюнтер М. (1997). «Ориентированные матроиды». В Гудман, Джейкоб Э. ; О'Рурк, Джозеф (ред.). Справочник по дискретной и вычислительной геометрии. Бока-Ратон: CRC Press. С. 111–132.

Статьи

А. Бахем, А. Ванка, Теоремы разделения для ориентированных матроидов, Дискретная математика. 70 (1988) 303–310.
Роберт Г. Бланд, Новые правила конечного поворота для симплекс-метода, Math. Опер. Res. 2 (1977) 103–107.
Фолкман, Джон ; (Октябрь 1978 г.). «Ориентированные матроиды». J. Combin. Теория Сер. Б. 25 (2): 199–236. DOI : 10.1016 / 0095-8956 (78) 90039-4.
; Терлаки, Тамаш (1997). Томас М. Либлинг; Доминик де Верра (ред.). «Перекрестные методы: свежий взгляд на алгоритмы разворота». Математическое программирование, серия B. 79 (1–3). Амстердам: North-Holland Publishing Co., стр. 369–395. doi : 10.1007 / BF02614325. MR 1464775.
; Намики, Макото (март 1994). «Об экстремальном поведении метода наименьшего индекса Мурти». Математическое программирование. 64 (1): 365–370. doi : 10.1007 / BF01582581. MR 1286455.
Иллеш, Тибор; Сирмаи, Акос; Терлаки, Тамаш (1999). «Метод конечных крестов для гиперболического программирования». Европейский журнал операционных исследований. 114 (1): 198–214. CiteSeerX 10.1.1.36.7090. DOI : 10.1016 / S0377-2217 (98) 00049-6. ISSN 0377-2217.
R. Тиррелл Рокафеллар. Элементарные векторы подпространства $R n {\ displaystyle R ^ {n}}$ $R ^ {n}$ , в Комбинаторной математике и ее приложениях, Р. К. Бозе и Т. А. Даулинг (ред.), Univ. of North Carolina Press, 1969, 104–127.
Roos, C. (1990). «Экспоненциальный пример правила поворота Терлаки для симплексного метода крест-накрест». Математическое программирование. Серия A. 46 (1): 79–84. doi : 10.1007 / BF01585729. MR 1045573.
Терлаки, Т. (1985). «Конвергентный крест-накрест». Оптимизация: журнал математического программирования и исследования операций. 16 (5): 683–690. doi : 10.1080 / 02331938508843067. ISSN 0233-1934. MR 0798939.
(1987). «Метод конечных крестовин для ориентированных матроидов». Журнал комбинаторной теории. Серия B. 42 (3): 319–327. DOI : 10.1016 / 0095-8956 (87) 90049-9. ISSN 0095-8956. MR 0888684.
Терлаки, Тамаш; Чжан, Шу Чжун (1993). «Правила поворота для линейного программирования: обзор последних теоретических разработок». Анналы исследований операций. 46–47 (1): 203–233. CiteSeerX 10.1.1.36.7658. DOI : 10.1007 / BF02096264. ISSN 0254-5330. MR 1260019.
Майкл Дж. Тодд, Линейное и квадратичное программирование в ориентированных матроидах, J. Combin. Теория Сер. B 39 (1985) 105-133.
Ван Чжэ Минь (1987). "Конечный алгоритм без конформного исключения над ориентированным матроидным программированием". Китайские анналы математики (Shuxue Niankan B Ji). Серия B. 8 (1): 120–125. ISSN 0252-9599. MR 0886756.

В Интернете

Ziegler, Günter (1998). «Ориентированные матроиды сегодня». Электронный журнал комбинаторики.
Малькевич, Джозеф. «Ориентированные матроиды: сила объединения». Столбец функций. Американское математическое общество. Проверено 14 сентября 2009 г.

Внешние ссылки