(Перенаправлено с объекта Natural number )
В теории категорий объект натуральных чисел ( NNO) - это объект, наделенный рекурсивной структурой, подобной натуральным числам. Точнее, в категории E с конечным объектом 1 NNO N задается следующим образом:
- глобальный элемент г : 1 → N, и
- стрелка s : N → N,
такая, что для любого объекта A из E, глобального элемента q : 1 → A и стрелки f : A → A существует единственная стрелка u : N → A такая, что:
- u ∘ z = q, и
- у ∘ ы = е ∘ у.
Другими словами, треугольник и квадрат на следующей диаграмме коммутируют.
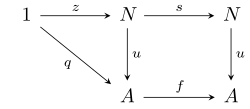
Пара ( q, f) иногда называется рекурсивными данными для u, заданными в форме рекурсивного определения :
- ⊢ u ( z) = q
- y ∈ E N ⊢ u ( s y) = f ( u ( y))
Приведенное выше определение является универсальным свойством NNO, то есть они определены с точностью до канонического изоморфизма. Если указанная выше стрелка u просто должна существовать, то есть уникальность не требуется, то N называется слабым NNO.
Содержание
- 1 Эквивалентные определения
- 2 свойства
- 3 Примеры
- 4 См. Также
- 5 ссылки
- 6 Внешние ссылки
Эквивалентные определения
NNO в декартовых замкнутых категориях (CCC) или топоах иногда определяются следующим эквивалентным образом (из-за Ловера ): для каждой пары стрелок g : A → B и f : B → B существует единственный h : N × A → B такие, что квадраты на следующей диаграмме коммутируют.

Эта же конструкция определяет слабые NNO в декартовых категориях, которые не являются декартово замкнутыми.
В категории с терминальным объектом 1 и бинарными копроизведениями (обозначаемых +), AN NNO может быть определен как исходная алгебра в endofunctor, который действует на объектах с помощью X ↦ 1 + X и на стрелки с помощью F ↦ [ID 1, х ].
Свойства
- Каждый НСО является исходным объектом категории диаграмм вида

- Если декартова замкнутая категория имеет слабые NNO, то каждый ее фрагмент также имеет слабые NNO.
- ННО могут быть использованы для нестандартных моделей в теории типа в аналогично тому, нестандартные модели анализа. Такие категории (или топои) имеют тенденцию иметь «бесконечно много» нестандартных натуральных чисел. (Как всегда, есть простые способы получить нестандартные NNO; например, если z = sz, и в этом случае категория или topos E тривиальны.)
- Фрэйд показал, что г и s образуют копроизведение диаграмму для ННО; также, ! N : N → 1 представляет собой коуравнитель из й и 1 Н, то есть, каждая пара глобальных элементов N соединена посредством S ; кроме того, эта пара фактов характеризует все ННО.
Примеры
- В Set, категории наборов, стандартные натуральные числа являются NNO. Терминальный объект в Set является синглтоном, а функция из синглтона выбирает единственный элемент набора. Натуральные числа 𝐍 - это NNO, где z - функция от одноэлементного до 𝐍, изображение которой равно нулю, а s - функция-последователь. (На самом деле мы могли бы позволить z выбрать любой элемент из 𝐍, и результирующий NNO был бы изоморфен этому.) Можно доказать, что диаграмма в определении коммутирует, используя математическую индукцию.
- В категории типов теории типов Мартина-Лёфа (с типами как объектами и функциями как стрелками) стандартный тип натуральных чисел nat является ННО. Можно использовать рекурсор для nat, чтобы показать, что соответствующая диаграмма коммутирует.
- Предположим, что является Гротендика топос с терминала объекта и что для некоторой топологии Гротендика на категории. Тогда, если - постоянный предпучок на, то NNO в пучке, и можно показать, что он принимает форму










Смотрите также
Ссылки
- Джонстон, Питер Т. (2002). Эскизы слона: сборник теории топоса. Оксфорд: Издательство Оксфордского университета. ISBN 0198534256. OCLC 50164783.
- Ловер, Уильям (2005) [1964]. «Элементарная теория категории множеств (полная версия) с комментариями». Отпечатки в теории и приложениях категорий. 11: 1–35.
внешние ссылки

