Функция Mittag-Leffler

редактировать

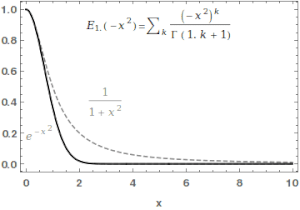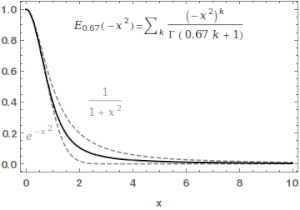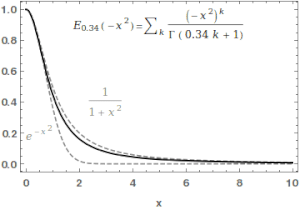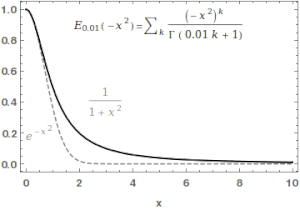
Функцию Миттаг-Леффлера можно использовать для непрерывной интерполяции между функцией Гаусса и Лоренца.

В математике Функция Миттаг-Леффлера E α, β - это специальная функция, комплексная функция, которая зависит от двух комплексные параметры α и β. Это может быть определено следующей рядом, когда действительная часть α строго положительна:

E α, β (z) = ∑ k = 0 ∞ z k Γ (α k + β). {\ displaystyle E _ {\ alpha, \ beta} (z) = \ sum _ {k = 0} ^ {\ infty} {\ frac {z ^ {k}} {\ Gamma (\ alpha k + \ beta)}}.}

E _ {{\ alpha, \ beta}} (z) = \ sum _ {{k = 0} } ^ {\ infty} {\ frac {z ^ {k}} {\ Gamma (\ alpha k + \ beta)}}.

где $Γ (x) {\ displaystyle \ Gamma (x)}$ ${\ displaystyle \ Gamma (x)}$ - это гамма-функция. Когда $β = 1 {\ displaystyle \ beta = 1}$ $\ beta = 1$ , оно сокращается как $E α (z) = E α, 1 (z) {\ displaystyle E _ {\ alpha}. (z) = E _ {\ alpha, 1} (z)}$ ${\ displaystyle E _ {\ alpha} (z) = E _ {\ alpha, 1} (z)}$ . Для $α = 0 {\ displaystyle \ alpha = 0}$ $\ alpha = 0$ указанный выше ряд равен разложению Тейлора геометрического ряда и, следовательно, $E 0, β (z) = 1 Γ (β) 1 1 - z {\ displaystyle E_ {0, \ beta} (z) = {\ frac {1} {\ Gamma (\ beta)}} {\ frac {1} {1-z}}}$ ${\ displaystyle E_ {0, \ beta} (z) = {\ frac {1} {\ Gamma (\ beta)}} {\ frac {1} {1-z}}}$ .

В случае, когда α и β действительны и положительны, ряд сходится для всех значений аргумента z, поэтому функция Миттаг-Леффлера является целой функцией. Эта функция названа в честь Гёста Миттаг-Леффлер. Этот класс функций важен в теории дробного исчисления.

Для α>0 функция Миттаг-Леффлера $E α, 1 (z) {\ displaystyle E _ {\ alpha, 1} ( z)}$ ${\ displaystyle E _ {\ alpha, 1} (z)}$ - целая функция порядка 1 / α и в некотором смысле простейшая целая функция этого порядка.

Функция Миттаг-Леффлера удовлетворяет свойству рекуррентности (теорема 5.1 из)

E α, β (z) = 1 z E α, β - α (z) - 1 z Γ (β - α), {\ displaystyle E _ {\ alpha, \ beta} (z) = {\ frac {1} {z}} E _ {\ alpha, \ beta - \ alpha} (z) - {\ frac {1} {z \ Gamma (\ beta - \ alpha),}}}

{\ displaystyle E _ {\ alpha, \ beta} (z) = {\ frac {1} {z }} E _ {\ alpha, \ beta - \ alpha} (z) - {\ frac {1} {z \ Gamma (\ beta - \ alpha),}}}

откуда асимптотическое разложение Пуанкаре

E α, β (z) ∼ - ∑ k = 1 1 zk Γ (β - k α) {\ displaystyle E _ {\ alpha, \ beta} (z) \ sim - \ sum _ {k = 1} {\ frac {1} {z ^ {k} \ Gamma (\ beta -k \ alpha)}}}

{\ displaystyle E_ { \ alpha, \ beta} (z) \ sim - \ sum _ {k = 1} {\ frac {1} {z ^ {k} \ Gamma (\ beta -k \ alpha)}}}

следует, что верно для $z → - ∞ {\ displaystyle z \ to - \ infty}$ ${\ displaystyle z \ to - \ infty}$ .

Содержание

1 Особые случаи
2 Интегральное представление Миттаг-Леффлера
3 См. также
4 Примечания
5 Ссылки
6 Внешние ссылки

Особые случаи

Для $α = 0, 1/2, 1, 2 {\ displaystyle \ alpha = 0, 1 / 2,1,2}$ $\ alpha = 0,1 / 2,1,2$ находим: (Раздел 2)

Функция ошибки :

E 1 2 (z) = exp ⁡ (z 2) erfc ⁡ (- z). {\ displaystyle E _ {\ frac {1} {2}} (z) = \ exp (z ^ {2}) \ operatorname {erfc} (-z).}

{\ displaystyle E _ {\ frac {1} {2}} (z) = \ exp (z ^ {2}) \ operatorname {erfc} (-z).}

Сумма геометрической прогрессии :

E 0 (z) = ∑ k = 0 ∞ zk = 1 1 - z, | z | < 1. {\displaystyle E_{0}(z)=\sum _{k=0}^{\infty }z^{k}={\frac {1}{1-z}},\,|z|<1.}

{\ displaystyle E_ {0} (z) = \ sum _ {к = 0} ^ {\ infty} z ^ {k} = {\ frac {1} {1-z}}, \, | z | <1.}

Показательная функция :

E 1 (z) = ∑ k = 0 ∞ z k Γ (k + 1) = ∑ k = 0 ∞ z k k! = ехр ⁡ (z). {\ Displaystyle E_ {1} (z) = \ sum _ {k = 0} ^ {\ infty} {\ frac {z ^ {k}} {\ Gamma (k + 1)}} = \ sum _ {k = 0} ^ {\ infty} {\ frac {z ^ {k}} {k!}} = \ Exp (z).}

{\ displaystyle E_ {1} (z) = \ sum _ {k = 0} ^ {\ infty} {\ frac {z ^ {k}} {\ Gamma (k + 1)}} = \ sum _ {k = 0} ^ {\ infty} {\ гидроразрыв {z ^ {k}} {k!}} = \ exp (z).}

Гиперболический косинус :

E 2 (z) = cosh ⁡ (z), и E 2 (- z 2) = cos ⁡ (z). {\ displaystyle E_ {2} (z) = \ cosh ({\ sqrt {z}}), {\ text {и}} E_ {2} (- z ^ {2}) = \ cos (z).}

{\ displaystyle E_ {2 } (z) = \ cosh ({\ sqrt {z}}), {\ text {и}} E_ {2} (- z ^ {2}) = \ cos (z).}

Для $β = 2 {\ displaystyle \ beta = 2}$ $\ beta = 2$ имеем

E 1, 2 (z) = ez - 1 z, {\ displaystyle E_ {1, 2} (z) = {\ frac {e ^ {z} -1} {z}},}

{\ displaystyle E_ {1,2} (z) = {\ frac {e ^ {z} -1} {z}},}

E 2, 2 (z) = sh ⁡ (z) z. {\ displaystyle E_ {2,2} (z) = {\ frac {\ sinh ({\ sqrt {z}})} {\ sqrt {z}}}.}

{\ displaystyle E_ {2,2} (z) = {\ frac {\ sinh ( {\ sqrt {z}})} {\ sqrt {z}}}.}

Для $α = 0, 1, 2 {\ displaystyle \ alpha = 0,1,2}$ $\ альфа = 0,1,2$ , интеграл

∫ 0 z E α (- s 2) ds {\ displaystyle \ int _ {0} ^ {z } E _ {\ alpha} (- s ^ {2}) \, {\ mathrm {d}} s}

{\ displaystyle \ int _ {0} ^ {z} E_ { \ alpha} (- s ^ {2}) \, {\ mathrm {d}} s}

дает соответственно: $arctan ⁡ (z) {\ displaystyle \ arctan (z)}$ $\ arctan (z)$ , $π 2 erf ⁡ (z) {\ displaystyle {\ tfrac {\ sqrt {\ pi}} {2}} \ operatorname {erf} (z)}$ ${\ tfrac {{\ sqrt {\ pi}}} {2}} \ operatorname {erf} (z)$ , $грех ⁡ (z) {\ displaystyle \ sin ( z)}$ $\ sin (z)$ .

Интегральное представление Миттаг-Леффлера

Интегральное представление функции Миттаг-Леффлера: (Раздел 6)

E α, β (z) = 1 2 π i ∫ C t α - β ett α - zdt, ℜ (α)>0, ℜ (β)>0, {\ displaystyle E _ {\ alpha, \ beta} (z) = {\ frac {1} {2 \ pi i}} \ int _ {C} {\ frac {t ^ {\ alpha - \ beta} e ^ {t}} {t ^ {\ alpha} -z}} \, dt, \ Re (\ alpha)>0, \ Re (\ beta)>0,}

E_{\alpha,\beta }(z)={\frac {1}{2\pi i}}\int _{C}{\frac {t^{\alpha -\beta }e^{t}}{t^{\alpha }-z}}\,dt,\Re (\alpha)>0, \ Re (\ beta)>0,

где c на обходе C начинается и заканчивается на −∞ и проходит вокруг особенностей и точек ветвления подынтегрального выражения.

Связанное с преобразованием Лапласа и суммирование Миттаг-Леффлера является выражением (уравнение (7.5) для, с m = 0)

∫ 0 ∞ e - tzt β - 1 E α, β (± rt α) dt = z α - β z α ∓ r, ℜ (z)>0, ℜ (α)>0, ℜ (β)>0. {\ displaystyle \ int _ {0} ^ {\ infty} e ^ {- tz} t ^ {\ beta -1} E _ {\ alpha, \ beta} (\ pm r \, t ^ {\ alpha}) \, dt = {\ frac {z ^ {\ alpha - \ beta}} {z ^ {\ alpha} \ mp r}}, \ Re (z)>0, \ Re (\ alpha)>0, \ Re ( \ beta)>0.}

\int _{0}^{\infty }e^{-tz}t^{\beta -1}E_{\alpha,\beta }(\pm r\,t^{\alpha })\,dt={\frac {z^{\alpha -\beta }}{z^{\alpha }\mp r}},\Re (z)>0, \ Re (\ alpha)>0, \ Re (\ beta)>0.

См. также

Notes

R Пакет 'MittagLeffleR' от Gurtek Gill, Peter Straka. Реализует функцию Mittag-Leffler, распределение, генерацию случайных переменных и оценку.

Ссылки

Mittag- Leffler, MG: Sur la nouvelle fonction E (x). CR Acad. Sci. Paris 137, 554–558 (1903)
Mittag-Leffler, MG: Sopra la funzione E˛.x /. Rend. R. Acc. Lincei, (Ser. 5) 13, 3–5 (1904)
Горенфло Р., Килбас А. А., Майнарди Ф., Рогозин С. В., Функции Миттаг-Леффлера, связанные темы и приложения (Спрингер, Нью-Йорк к, 2014) 443 с. ISBN 978-3-662-43929-6
Игорь Подлубный (1998). "глава 1". Дробные дифференциальные уравнения. Введение в дробные производные, дробные дифференциальные уравнения, некоторые методы их решения и некоторые их приложения. Математика в науке и технике. Академическая пресса. ISBN 0-12-558840-2.
Кай Дитхельм (2010). "Глава 4". Анализ дробных дифференциальных уравнений: прикладное изложение с использованием дифференциальных операторов типа Капуто. Конспект лекций по математике. Гейдельберг и Нью-Йорк: Springer-Verlag. ISBN 978-3-642-14573-5.

Внешние ссылки

Эта статья включает материал из функции Миттаг-Леффлера на PlanetMath, которая под лицензией Creative Commons Attribution / Share-Alike License.