Задача решетки

редактировать

В информатике, задачи решетки являются классом оптимизации задачи, связанные с математическими объектами, называемыми решетками. Предполагаемая неразрешимость таких проблем играет центральную роль в построении безопасных криптосистем на основе решеток : решетчатые проблемы являются примером NP-сложных проблем, которые, как было показано, являются сложными в среднем случае., предоставляя тестовый пример безопасности криптографических алгоритмов. Кроме того, некоторые проблемы решетки, которые являются наихудшими трудностями, могут использоваться в качестве основы для чрезвычайно безопасных криптографических схем. Использование в таких схемах жесткости наихудшего случая делает их одними из очень немногих схем, которые, скорее всего, защищены даже от квантовых компьютеров. Для приложений в таких криптосистемах решетки в векторном пространстве (часто $Q n {\ displaystyle \ mathbb {Q} ^ {n}}$ $\ mathbb {Q } ^ n$ ) или бесплатные модули (часто $Z n {\ displaystyle \ mathbb {Z} ^ {n}}$ $\ mathbb {Z} ^ {n}$ ) обычно рассматриваются.

Для всех задач ниже предположим, что нам даны (в дополнение к другим более конкретным входным данным) базис для векторного пространства V и norm N. Обычно рассматривается евклидова норма L. Однако другие нормы (такие как L ) также учитываются и отображаются в различных результатах. Пусть $λ (L) {\ displaystyle \ lambda (L)}$ $\ lambda (L)$ обозначает длину кратчайшего ненулевого вектора в решетке L, то есть

λ (L) = min v ∈ L ∖ {0} ‖ v ‖ N. {\ displaystyle \ lambda (L) = \ min _ {v \ in L \ smallsetminus \ {\ mathbf {0} \}} \ | v \ | _ {N}.}

{\ displaystyle \ lambda (L) = \ min _ {v \ in L \ smallsetminus \ {\ mathbf {0} \}} \ | v \ | _ {N}.}

Содержание

1 кратчайший вектор проблема (SVP)
- 1.1 Результаты твердости
- 1.2 Алгоритмы для евклидовой нормы
2 GapSVP
3 Ближайшая векторная задача (CVP)
- 3.1 Связь с SVP
- 3.2 Результаты твердости
- 3.3 Сферное декодирование
4 GapCVP
- 4.1 Известные результаты
5 Задача наикратчайших независимых векторов (SIVP)
6 Декодирование с ограниченным расстоянием
7 Проблема радиуса покрытия
8 Задача на кратчайший базис
9 Использование в криптографии
10 См. Также
11 Ссылки
12 Дополнительная литература

Задача кратчайшего вектора (SVP)

Это иллюстрация задачи кратчайшего вектора (базисные векторы синего цвета, кратчайший вектор в красный).

В SVP базис векторного пространства V и norm N (часто L ) являются задано для решетки L, и нужно найти кратчайший ненулевой вектор в V, измеренный N, в L. Другими словами, алгоритм должен вывести ненулевой вектор v такое, что $N (v) = λ (L) {\ displaystyle N (v) = \ lambda (L)}$ $N (v) = \ lambda (L)$ .

В версии SVP γ γ-приближения необходимо найти ненулевой вектор решетки длины не более $γ ⋅ λ (L) {\ displaystyle \ gamma \ cdot \ lambda (L)}$ ${\ displaystyle \ gamma \ cdot \ lambda (L)}$ для данного $γ ≥ 1 {\ displaystyle \ gamma \ geq 1}$ ${\ displaystyle \ gamma \ geq 1}$ .

Результаты твердости

Точная версия проблемы известна только как NP-жесткий для рандомизированных сокращений.

Напротив, соответствующие задача относительно равномерной нормы известна как NP-сложная.

Алгоритмы для евклидовой нормы

Чтобы решить точную версию SVP при евклидовой норме, Известно несколько различных подходов, которые можно разделить на два класса: алгоритмы, требующие сверхэкспоненциального времени ( $2 ω (n) {\ displaystyle 2 ^ {\ omega (n)}}$ $2 ^ {\ omega (n)}$ ) и $поли ⁡ (n) {\ displaystyle \ operatorname {poly} (n)}$ ${\ displaystyle \ operatorname {poly} (n)}$ память и алгоритмы, требующие экспоненциального времени и пространства ( $2 Θ (n) {\ displaystyle 2 ^ {\ Theta (n)}}$ ${\ displaystyle 2 ^ {\ Theta (n)}}$ ) в размерности решетки. Первый класс алгоритмов, в первую очередь, включает в себя решетчатую нумерацию и сокращение случайной выборки, в то время как второй включает решетчатое просеивание, вычисление ячейки Вороного решетки и дискретную гауссовскую выборку. Открытая проблема заключается в том, существуют ли алгоритмы для решения точного SVP, работающие за одно экспоненциальное время ( $2 O (n) {\ displaystyle 2 ^ {O (n)}}$ $2 ^ {{O (n)}}$ ) и требующие полиномиального масштабирования памяти в размер решетки.

Для решения версии γ-приближения SVP γ для $γ>1 {\ displaystyle \ gamma>1}$ $\gamma>1$ для евклидовой нормы наиболее известные подходы основаны на использовании уменьшение базиса решетки. Для больших $γ = 2 Ω (n) {\ displaystyle \ gamma = 2 ^ {\ Omega (n)}}$ ${\ displaystyle \ gamma = 2 ^ {\ Omega (n)}}$ Lenstra – Lenstra– Алгоритм Ловаса (LLL) может найти решение за время, полиномиальное в размерности решетки. Для меньших значений $γ {\ displaystyle \ gamma}$ $\ gamma$ алгоритм Блока Коркина-Золотарева (BKZ) является обычно используется, когда входные данные алгоритма (размер блока $β {\ displaystyle \ beta}$ $\ beta$ ) определяют временную сложность и качество вывода: для больших коэффициентов аппроксимации $γ {\ displaystyle \ gamma }$ $\ gamma$ , достаточно небольшого размера блока $β {\ displaystyle \ beta}$ $\ beta$ , и алгоритм быстро завершает работу у. Для небольших $γ {\ displaystyle \ gamma}$ $\ gamma$ необходимы более крупные $β {\ displaystyle \ beta}$ $\ beta$ , чтобы найти достаточно короткие векторы решетки, и алгоритм занимает больше времени найти решение. Алгоритм BKZ внутренне использует точный алгоритм SVP в качестве подпрограммы (работающий в решетках с размером не более $β {\ displaystyle \ beta}$ $\ beta$ ), и его общая сложность тесно связана с затратами на эти Звонки SVP в измерении $β {\ displaystyle \ beta}$ $\ beta$ .

GapSVP

Проблема GapSVP β состоит в различении экземпляров SVP, в которых длина самого короткого вектора не более $1 {\ displaystyle 1}$ $1$ или больше $β {\ displaystyle \ beta}$ $\ beta$ , где $β {\ displaystyle \ beta}$ $\ beta$ может быть фиксированной функцией размера решетки $n {\ displaystyle n}$ $n$ . Учитывая основу решетки, алгоритм должен решить, будет ли $λ (L) ≤ 1 {\ displaystyle \ lambda (L) \ leq 1}$ $\ lambda (L) \ leq 1$ или $λ (L)>β { \ displaystyle \ lambda (L)>\ beta}$ $\lambda(L)>\ beta$ . Как и другие проблемы с обещаниями, алгоритм может ошибаться во всех других случаях.

Еще одна версия проблемы - GapSVP ζ, γ для некоторых функций $ζ, γ {\ displaystyle \ zeta, \ gamma}$ $\ zeta, \ gamma$ . Входными данными для алгоритма является базис $B {\ displaystyle B}$ $B$ и число $d {\ displaystyle d}$ $d$ . Гарантируется, что все векторы в ортогонализации Грама – Шмидта имеют длину не менее 1, и что $λ (L (B)) ≤ ζ (n) {\ displaystyle \ lambda (L (B)) \ leq \ zeta (n)}$ $\ lambda (L (B)) \ leq \ zeta (n)$ и что $1 ≤ d ≤ ζ (n) / γ (n) {\ displaystyle 1 \ leq d \ leq \ zeta (n) / \ gamma (n)}$ $1 \ leq d \ leq \ zeta (n) / \ gamma (n)$ где $n {\ displaystyle n}$ $n$ - размер. Алгоритм должен принять, если $λ (L (B)) ≤ d {\ displaystyle \ lambda (L (B)) \ leq d}$ $\ lambda (L (B)) \ leq d$ , и отклонить, если $λ (L (B)) ≥ γ (n). d {\ displaystyle \ lambda (L (B)) \ geq \ gamma (n).d}$ $\ lambda (L (B)) \ geq \ gamma (n).d$ . Для больших $ζ {\ displaystyle \ zeta}$ $\ zeta$ ( $ζ (n)>2 n / 2 {\ displaystyle \ zeta (n)>2 ^ {n / 2}}$ $\zeta(n)>2 ^ { n / 2}$ ), проблема в эквивалент GapSVP γ, поскольку предварительная обработка, выполненная с использованием алгоритма LLL, делает второе условие (и, следовательно, $ζ {\ displaystyle \ zeta}$ $\ zeta$ ) избыточным.

Задача ближайшего вектора (CVP)

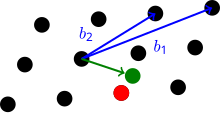
Это иллюстрация ближайшей векторной задачи (базисные векторы синим, внешний вектор зеленым, ближайший вектор красным).

В CVP базис векторного пространства V и метрики M (часто L ) даны для решетки L, а также вектор v в V, но не обязательно в L. Желательно, чтобы найти вектор в L, ближайший к v (измеренный с помощью M). В $γ {\ displaystyle \ gamma}$ $\ gamma$ -приближенной версии CVP γ необходимо найти решетку вектор на расстоянии в mo st $γ {\ displaystyle \ gamma}$ $\ gamma$ .

Связь с SVP

Ближайшая векторная задача - это обобщение задачи наикратчайшего вектора. Легко показать, что, имея oracle для CVP γ (определено ниже), можно решить SVP γ, сделав несколько запросов к оракулу. Наивный метод поиска кратчайшего вектора путем вызова оракула CVP γ для поиска вектора, ближайшего к 0, не работает, потому что 0 сам по себе является вектором решетки, и алгоритм потенциально может вывести 0.

Уменьшение от SVP γ до CVP γ выглядит следующим образом: Предположим, что входные данные для задачи SVP γ являются основой для решетки $B = [b 1, b 2,…, bn] {\ displaystyle B = [b_ {1}, b_ {2}, \ ldots, b_ {n}]}$ $B = [b_1, b_2, \ ldots, b_n ]$ . Рассмотрим базис $B i = [b 1,…, 2 bi,…, bn] {\ displaystyle B ^ {i} = [b_ {1}, \ ldots, 2b_ {i}, \ ldots, b_ { n}]}$ $B ^ i = [b_1, \ ldots, 2b_i, \ ldots, b_n]$ и пусть $xi {\ displaystyle x_ {i}}$ $x_ {i}$ будет вектором, возвращаемым CVP γ (B, b я). Утверждение состоит в том, что кратчайший вектор в наборе ${x i - b i} {\ displaystyle \ {x_ {i} -b_ {i} \}}$ $\ {x_i-b_i \}$ является самым коротким вектором в данной решетке.

Результаты твердости

Goldreich et al. показали, что любая твердость SVP подразумевает такую же твердость для CVP. Используя инструменты PCP, Arora et al. показал, что CVP трудно аппроксимировать в пределах фактора $2 log 1 - ϵ ⁡ (n) {\ displaystyle 2 ^ {\ log ^ {1- \ epsilon} (n)}}$ $2 ^ {\ log ^ {1- \ epsilon} (n)}$ , если $NP ⊆ DTIME ⁡ (2 поли ⁡ (журнал ⁡ N)) {\ Displaystyle \ OperatorName {NP} \ substeq \ OperatorName {DTIME} (2 ^ {\ operatorname {poly} (\ log n)})}$ ${\ displaystyle \ operatorname {NP} \ substeq \ operatorname {DTIME} (2 ^ { \ operatorname {poly} (\ log n)})}$ . Dinur et al. усилил это, дав результат NP-твердости с $ϵ = (log ⁡ log ⁡ n) c {\ displaystyle \ epsilon = (\ log \ log n) ^ {c}}$ $\ epsilon = (\ log \ log n) ^ c$ для $c < 1 / 2 {\displaystyle c<1/2}$ $c <1/2$ .

Сферное декодирование

Алгоритмы для CVP, особенно вариант Fincke и Pohst, использовались для обнаружения данных в системах беспроводной связи с множеством входов и множеством выходов (MIMO ) (для кодированных и некодированных). сигналы). В этом контексте это называется сферическим декодированием из-за радиуса, используемого внутри многих решений CVP.

Он был применен в области разрешения целочисленной неоднозначности GNSS (GPS) фазы несущей. В этой области это называется методом LAMBDA.

GapCVP

Эта проблема аналогична проблеме GapSVP. Для GapSVP β входные данные состоят из основы решетки и вектора $v {\ displaystyle v}$ $v$ , и алгоритм должен ответить, выполняется ли одно из следующих условий:

существует такой вектор решетки, что расстояние между ним и $v {\ displaystyle v}$ $v$ не больше 1.
каждый вектор решетки находится на расстоянии больше, чем $β {\ displaystyle \ beta}$ $\ beta$ от $v {\ displaystyle v}$ $v$ .

Противоположное условие - ближайший вектор решетки находится на расстоянии $1 < λ ( L) ≤ β {\displaystyle 1<\lambda (L)\leq \beta }$ ${ \ displaystyle 1 <\ lambda (L) \ leq \ beta}$ , отсюда и название GapCVP.

Известные результаты

Проблема тривиально содержится в NP для любого коэффициента приближения.

Шнорр в 1987 году показал, что детерминированные алгоритмы полиномиального времени могут решить проблему для $β = 2 O (n (log ⁡ log ⁡ n) 2 / log ⁡ n) {\ displaystyle \ beta = 2 ^ {O (n (\ log \ log n) ^ {2} / \ log n)}}$ $\ beta = 2 ^ {O (n (\ log \ log n) ^ 2 / \ log n)}$ . Ajtai et al. показали, что вероятностные алгоритмы могут достичь немного лучшего коэффициента приближения $β = 2 O (n log ⁡ log ⁡ n / log ⁡ n) {\ displaystyle \ beta = 2 ^ {O (n \ log \ log n / \ log n)}}$ $\ beta = 2 ^ {O (n \ log \ log n / \ log n)}$ .

В 1993 году Банашчик показал, что GapCVP n находится в $NP ∩ co NP {\ displaystyle {\ mathsf {NP \ cap coNP}}}$ ${\ displaystyle {\ mathsf { NP \ cap coNP}}}$ . В 2000 году Голдрайх и Гольдвассер показали, что $β = n / log ⁡ n {\ displaystyle \ beta = {\ sqrt {n / \ log n}}}$ $\ beta = \ sqrt {n / \ log n}$ ставит проблему как в NP, так и в coAM. В 2005 году Ааронов и Регев показали, что для некоторой константы $c {\ displaystyle c}$ $c$ проблема с $β = cn {\ displaystyle \ beta = c {\ sqrt {n}} }$ $\ beta = c \ sqrt {n}$ находится в $NP ∩ co NP {\ displaystyle {\ mathsf {NP \ cap coNP}}}$ ${\ displaystyle {\ mathsf { NP \ cap coNP}}}$ .

Для нижних границ Dinur et al. в 1998 году показал, что проблема NP-трудна для $β = no (1 / log ⁡ log ⁡ n) {\ displaystyle \ beta = n ^ {o (1 / \ log {\ log {n}})} }$ $\ beta = n ^ {o (1 / \ log {\ log {n}})}$ .

Задача кратчайших независимых векторов (SIVP)

Для решетки L размерности n алгоритм должен вывести n линейно независимых $v 1, v 2,…, vn {\ displaystyle v_ {1}, v_ {2}, \ ldots, v_ {n}}$ $v_1, v_2, \ ldots, v_n$ так, чтобы $max ‖ vi ‖ ≤ max B ‖ bi ‖ {\ displaystyle \ max \ | v_ {i} \ | \ leq \ max _ {B} \ | b_ {i} \ |}$ ${\ displaystyle \ max \ | v_ {i} \ | \ leq \ max _ {B} \ | b_ {i} \ |}$ где правая часть рассматривает все основания $B = {b 1,…, bn} { \ displaystyle B = \ {b_ {1}, \ ldots, b_ {n} \}}$ $B = \ {b_1, \ ldots, b_n \}$ решетки.

В $γ {\ displaystyle \ gamma}$ $\ gamma$ -приближенной версии, заданной решеткой L с размерностью n, найдите n линейно независимых векторов $v 1, v 2,…, vn {\ displaystyle v_ {1}, v_ {2}, \ ldots, v_ {n}}$ $v_1, v_2, \ ldots, v_n$ длины $max ‖ vi ‖ ≤ γ λ n ( L) {\ displaystyle \ max \ | v_ {i} \ | \ leq \ gamma \ lambda _ {n} (L)}$ ${\ displaystyle \ max \ | v_ { я} \ | \ leq \ gamma \ lambda _ {n} (L)}$ , где $λ n (L) {\ displaystyle \ lambda _ {n} (L)}$ $\ lambda_n (L)$ - это $n {\ displaystyle n}$ $n$ '-й последовательный минимум $L {\ displaystyle L}$ $L$ .

Ограниченное расстояние декодирование

Эта проблема аналогична CVP. Для вектора, расстояние от которого до решетки не превышает $λ (L) / 2 {\ displaystyle \ lambda (L) / 2}$ $\ lambda (L) / 2$ , алгоритм должен вывести ближайший к нему вектор решетки..

Проблема радиуса покрытия

При наличии основы для решетки алгоритм должен найти наибольшее расстояние (или, в некоторых версиях, его приближение) от любого вектора до решетки.

Проблема кратчайшего базиса

Многие проблемы становятся проще, если исходный базис состоит из коротких векторов. Алгоритм, который решает задачу кратчайшего базиса (SBP), должен, учитывая базис решетки $B {\ displaystyle B}$ $B$ , выводить эквивалентный базис $B '{\ displaystyle B'}$ $B'$ таким образом, чтобы длина самого длинного вектора в $B '{\ displaystyle B'}$ $B'$ была как можно короче.

Версия аппроксимации SBP γ проблема состоит в нахождении базиса, самый длинный вектор которого не более чем в $γ {\ displaystyle \ gamma}$ $\ gamma$ раз длиннее самого длинного вектор в кратчайшем базисе.

Использование в криптографии

Средний случай сложности проблем формирует основу для доказательства безопасности для большинства криптографических схем. Однако экспериментальные данные свидетельствуют о том, что большинству NP-сложных задач не хватает этого свойства: они, вероятно, только в худшем случае. Были выдвинуты гипотезы или доказано, что многие решеточные задачи являются сложными для среднего случая, что делает их привлекательным классом задач для построения криптографических схем. Более того, для создания безопасных криптографических схем использовалась жесткость наихудшего случая некоторых задач решетки. Использование в таких схемах жесткости наихудшего случая делает их одними из очень немногих схем, которые, скорее всего, безопасны даже против квантовых компьютеров.

Вышеупомянутые проблемы решетки легко решить, если алгоритм снабжен «хорошо» основание. Алгоритмы сокращения решетки стремятся, учитывая основу решетки, вывести новый базис, состоящий из относительно коротких, почти ортогональных векторов. Алгоритм сокращения базиса решетки Ленстры-Ленстры-Ловаса (LLL) был одним из первых эффективных алгоритмов для этой задачи, который мог выводить почти сокращенный базис решетки за полиномиальное время. Этот алгоритм и его дальнейшие усовершенствования были использованы для взлома нескольких криптографических схем, что сделало его очень важным инструментом криптоанализа. Успех LLL на экспериментальных данных привел к убеждению, что сокращение решетки может быть простой проблемой на практике. Однако это убеждение было оспорено, когда в конце 1990-х было получено несколько новых результатов о сложности решеточных задач, начиная с результата Ajtai.

. В своих основополагающих статьях Ajtai показал, что проблема SVP была NP- hard и обнаружил некоторые связи между сложностью наихудшего случая и сложностью среднего случая некоторых задач решетки. Основываясь на этих результатах, Аджтай и Дворк создали криптосистему с открытым ключом, безопасность которой может быть доказана с использованием только наихудшего уровня надежности определенной версии SVP, что сделало ее первым результатом использовать жесткость наихудшего случая для создания защищенных систем.

См. также

Ссылки

Дополнительная литература

Agrell, E.; Eriksson, T.; Варди, А.; Зегер, К. (2002). «Поиск ближайшей точки в решетках». IEEE Trans. Инф. Теория. 48 (8): 2201–2214. doi : 10.1109 / TIT.2002.800499.
Micciancio, Daniele (2001). «Задачу кратчайшего вектора {NP} трудно аппроксимировать с точностью до некоторой константы». SIAM Journal on Computing. 30 (6): 2008–2035. CiteSeerX 10.1.1.93.6646. doi : 10.1137 / S0097539700373039.
Nguyen, Phong Q.; Стерн, Жак (2000). «Сокращение решетки в криптологии: обновление». Материалы 4-го Международного симпозиума по алгоритмической теории чисел. Springer-Verlag. С. 85–112. ISBN 978-3-540-67695-9.