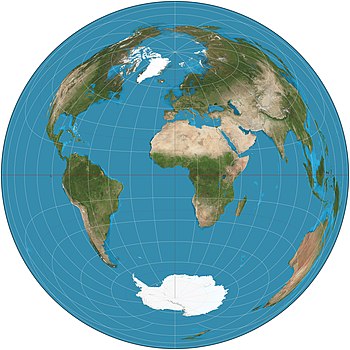
Азимутальная равновеликая проекция Ламберта

Азимутальная равновеликая проекция мира Ламберта. Центр - 0 ° N 0 ° E. Антипод - 0 ° N 180 ° E, около Кирибати в Тихом океане. Эта точка представлена ​​всей круговой границей карты, и океан вокруг этой точки появляется вдоль всей границы. Азимутальная равновеликая проекция Ламберта с индикатрисой деформации Тиссо.

Азимутальная равновеликая проекция Ламберта представляет собой конкретное отображение сферы на диск. Он точно представляет область во всех областях сферы, но не точно представляет углы. Он назван в честь швейцарского математика Иоганна Генриха Ламберта, объявившего его в 1772 году. «Зенитал» является синонимом «азимутального», проекция также известна как Ламберт. зенитная равновеликая проекция .

Азимутальная проекция Ламберта используется как картографическая проекция в картографии. Например, Национальный атлас США использует азимутальную равновеликую проекцию Ламберта для отображения информации в онлайн-приложении Map Maker, а Европейское агентство по окружающей среде рекомендует использовать его для картографии Европы. для статистического анализа и отображения. Он также используется в таких научных дисциплинах, как геология для построения ориентации линий в трехмерном пространстве. Этому построению помогает специальный вид миллиметровой бумаги, который называется Сеть Шмидта.

• 1 Определение
• 2 Свойства
• 3 Приложения
• 4 Анимированная проекция Ламберта
• 5 См. Также
• 6 Ссылки
  • 6.1 Источники
• 7 Внешние ссылки

A поперечное сечение сферы и касательной к ней плоскости в точке S. Каждая точка на сфере (кроме антипода) проецируется на плоскость по дуге окружности с центром в точке касания между сферой и плоскостью.

Чтобы определить азимутальную проекцию Ламберта, представьте плоскость, касательную к сфере в точке некоторая точка S на сфере. Пусть P будет любой точкой на сфере, кроме антипода S. Пусть d будет расстоянием между S и P в трехмерном пространстве (а не расстоянием вдоль поверхности сферы). Затем проекция отправляет P в точку P 'на плоскости, которая находится на расстоянии d от S.

Чтобы сделать это более точным, существует уникальный круг с центром в S, проходящий через P и перпендикулярный плоскости самолет. Он пересекает плоскость в двух точках; пусть P ′ будет той, которая ближе к P. Это спроецированная точка. Смотрите рисунок. Антипод S исключен из проекции, потому что искомая окружность не единственна. Случай S вырожден; S проецируется на себя по окружности радиуса 0.

Для выполнения проекции на компьютере требуются явные формулы. Рассмотрим проекцию с центром в S = (0, 0, −1) на единичной сфере, которая представляет собой набор точек (x, y, z) в трехмерном пространстве R такое, что x + y + z = 1. В декартовых координатах (x, y, z) на сфере и (X, Y) на плоскости проекция и обратная ей проекция описываются как

$(X,\; Y)\; =\; (2\; 1\; -\; zx,\; 2\; 1\; -\; zy),\; (x,\; y,\; z)\; =\; (1\; -\; X\; 2\; +\; Y\; 2\; 4\; X,\; 1\; -\; X\; 2\; +\; Y\; 2\; 4\; Y,\; -\; 1\; +\; Х\; 2\; +\; У\; 2\; 2).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; (X,\; Y)\; =\; \backslash \; left\; (\{\backslash \; sqrt\; \{\backslash \; frac\; \{2\}\; \{1-z\}\}\}\; \backslash ,\; x,\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2\}\; \{1\})\; -z\}\}\}\; \backslash ,\; y\; \backslash \; right),\; \backslash \backslash \; (x,\; y,\; z)\; =\; \backslash \; left\; (\{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{X\; ^\; \{2\}\; +\; Y\; ^\; \{2\}\}\; \{4\; \}\}\}\}\; \backslash ,\; X,\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{X\; ^\; \{2\}\; +\; Y\; ^\; \{2\}\}\; \{4\}\}\}\}\; \backslash ,\; Y,\; -1\; +\; \{\backslash \; frac\; \{X\; ^\; \{\; 2\}\; +\; Y\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; right).\; \backslash \; End\; \{align\}\}\}$

В сферических координатах (φ, θ) на сфере (с φ зенит и θ азимут ) и полярные координаты (R, Θ) на диске, карта и ее обратная карта задаются как

$(R,\; \Theta )\; =\; (2\; cos\; \; \phi \; 2,\; \theta ),\; (\phi ,\; \theta )\; =\; (2\; arccos\; \; R\; 2,\; \Theta ).\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; (R,\; \backslash \; Theta)\; =\; \backslash \; left\; (2\; \backslash \; cos\; \{\backslash \; frac\; \{\backslash \; varphi\}\; \{2\}\},\; \backslash \; theta\; \backslash \; right),\; \backslash \backslash \; (\backslash \; varphi,\; \backslash \; theta)\; =\; \backslash \; left\; (2\; \backslash \; arccos\; \{\backslash \; frac\; \{R\}\; \{2\}\},\; \backslash \; Theta\; \backslash \; right).\; \backslash \; end\; \{align\}\}\}$

В цилиндрических координатах (r, θ, z) на сфере и полярные координаты (R, Θ) на плоскости, отображение и обратное к нему задаются формулами

$(R,\; \Theta )\; =\; (2\; (1\; +\; z),\; \theta ),\; (r,\; \theta ,\; z)\; =\; (R\; 1\; -\; R\; 2\; 4,\; \Theta ,\; -\; 1\; +\; R\; 2\; 2).\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнен\}\; (R,\; \backslash \; Theta)\; =\; \backslash \; left\; (\{\backslash \; sqrt\; \{2\; (1\; +\; z)\}\},\; \backslash \; theta\; \backslash \; right),\; \backslash \backslash \; (r,\; \backslash \; theta,\; z)\; =\; \backslash \; left\; (R\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{R\; ^\; \{2\}\}\; \{4\}\}\}\},\; \backslash \; Theta,\; -1\; +\; \{\backslash \; frac\; \{R\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; right).\; \backslash \; end\; \{align\}\}\}$

Проекция может быть центрирована в других точках и определена на сферах с радиусом, отличным от 1, используя аналогичные формулы.

Как определено в предыдущем разделе азимутальная проекция Ламберта единичной сферы не определена в (0, 0, 1). Он отправляет остальную часть сферы в открытый диск радиуса 2 с центром в начале координат (0, 0) на плоскости. Он отправляет точку (0, 0, −1) в (0, 0), экватор z = 0 в круг радиуса √2 с центром в (0, 0) и нижнюю полусферу z < 0 to the open disk contained in that circle.

. диффеоморфизм (биекция, которая бесконечно дифференцируема в обоих направлениях) между сферой (минус (0, 0, 1)) и открытым кругом радиуса 2. Это карта с сохранением площади (равная площадь), которую можно увидеть, вычислив элемент площади сферы, параметризованный с помощью обратной проекции. В декартовых координатах это

$d\; A\; =\; d\; X\; d\; Y.\; \{\backslash \; displaystyle\; dA\; =\; dX\; \backslash ;\; dY.\}$

Это означает, что измерение площади области на сфере равносильно измерению площади соответствующей области на диске.

С другой стороны, проекция не сохраняет угловые соотношения между кривыми на сфере. Никакое отображение между частью сферы и плоскостью не может сохранить и углы, и площади. (Если бы это было так, то это была бы локальная изометрия и сохраняла бы гауссову кривизну ; но сфера и диск имеют разные кривизны, поэтому это невозможно.) Этот факт, эта плоская картинки не могут идеально отображать области сфер, это фундаментальная проблема картографии.

Как следствие, области на сфере могут проецироваться на плоскость с сильно искаженными формами. Это искажение особенно заметно вдали от центра проекции (0, 0, -1). На практике проекция часто ограничивается полушарием с центром в этой точке; другое полушарие можно нанести на карту отдельно, используя вторую проекцию с центром в антиподе.

Азимутальная проекция Ламберта изначально задумывалась как проекция карты равной площади. Теперь он также используется в таких дисциплинах, как геология для построения данных направленности, как показано ниже.

Направление в трехмерном пространстве соответствует линии, проходящей через начало координат. Набор всех таких линий сам по себе является пространством, называемым реальной проективной плоскостью в математике. Каждая прямая, проходящая через начало координат, пересекает единичную сферу ровно в двух точках, одна из которых находится в нижней полусфере z ≤ 0. (Горизонтальные линии пересекают экватор z = 0 в двух противоположных точках. Понятно, что антиподальные точки на экваторе представляют (см. факторную топологию.) Следовательно, направления в трехмерном пространстве соответствуют (почти идеально) точкам в нижнем полушарии. Затем полусферу можно изобразить как диск радиуса √2, используя азимутальную проекцию Ламберта.

Таким образом, азимутальная проекция Ламберта позволяет нам наносить направления в виде точек на диске. Благодаря свойству проекции равных площадей, можно интегрировать по областям реальной проективной плоскости (пространству направлений) путем интегрирования по соответствующим областям на диске. Это полезно для статистического анализа данных о направлении, включая случайное жесткое вращение.

С помощью азимутальной проекции Ламберта можно построить не только линии, но и плоскости, проходящие через начало координат. Плоскость пересекает полусферу по дуге окружности, называемой следом плоскости, которая спускается вниз до кривой (обычно некруглой) в диске. Можно построить эту кривую или заменить плоскость перпендикулярной к ней линией, называемой полюсом, и вместо этого построить эту линию. Когда несколько плоскостей строятся вместе, нанесение полюсов вместо трасс позволяет получить менее загроможденный график.

Исследователи в области структурной геологии используют азимутальную проекцию Ламберта для построения кристаллографических осей и граней, линеаризации и слоистости в породы, сликенсайды в разломах и другие линейные и плоские объекты. В этом контексте проекция называется полусферической проекцией с равной площадью . Существует также равноугловая полусферическая проекция, определяемая стереографической проекцией.

В обсуждении здесь подчеркивается нижнее полушарие z ≤ 0, но некоторые дисциплины предпочитают верхнее полушарие z ≥ 0. Действительно, любое полушарие можно использовать для запишите линии через начало координат в трехмерном пространстве.

Сравнение азимутальной равновеликой проекции Ламберта и некоторых азимутальных проекций с центром на 90 ° северной широты в одном масштабе, упорядоченном по высоте проекции в радиусах Земли. (щелкните для подробностей) Анимация проекции Ламберта. Каждая ячейка сетки сохраняет свою площадь на протяжении всего преобразования. В этой анимации точки на экваторе всегда остаются на плоскости $z\; =\; 0\; \{\backslash \; displaystyle\; z\; =\; 0\}$. В этой анимированной проекции Ламберта южный полюс фиксируется.

Пусть $(u,\; \varphi )\; \{\backslash \; displaystyle\; (u,\; \backslash \; phi)\}$будет двумя параметрами, для которых и . Пусть $H\; \{\backslash \; displaystyle\; H\}$будет параметром «время» (равным высоте или вертикальной толщине оболочки в анимации). Если равномерная прямолинейная сетка нарисована в пространстве $(u,\; \varphi )\; \{\backslash \; displaystyle\; (u,\; \backslash \; phi)\}$, то любая точка в этой сетке преобразуется в точку $(x,\; y,\; z)\; \{\backslash \; displaystyle\; (x,\; y,\; z)\}$на сферической оболочке высотой $H\; \{\backslash \; displaystyle\; H\}$в соответствии с отображением

$Икс\; знак\; равно\; \lambda \; (u,\; ЧАС)\; соз\; \; (\varphi )\; \{\backslash \; Displaystyle\; x\; =\; \backslash \; lambda\; (u,\; H)\; \backslash \; cos\; (\backslash \; phi)\}$

$y\; =\; \lambda \; (u,\; H)\; sin\; \; (\varphi )\; \{\backslash \; displaystyle\; y\; =\; \backslash \; lambda\; (u,\; H)\; \backslash \; sin\; (\backslash \; phi)\}$

$z\; =\; H\; u\; 2\; \{\backslash \; displaystyle\; z\; =\; \{\backslash \; frac\; \{Hu\}\; \{2\}\}\}$

где $\lambda \; (\; u,\; H)\; знак\; равно\; 1\; 2\; (1\; -\; u)\; [8\; -\; H\; 2\; (1\; -\; u)]\; \{\backslash \; displaystyle\; \backslash \; lambda\; (u,\; H)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; sqrt\; \{(1\; -u)\; \backslash \; left\; [8-H\; ^\; \{2\}\; (1-u)\; \backslash \; right]\}\}\}$. Каждый кадр в анимации соответствует параметрическому графику деформированной сетки при фиксированном значении высоты оболочки $H\; \{\backslash \; displaystyle\; H\}$(в диапазоне от 0 до 2). Физически $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$- это растяжение (деформированная длина, деленная на исходную длину) бесконечно малой линии $d\; \varphi \; \{\backslash \; displaystyle\; d\; \backslash \; phi\}$отрезки линии. Это отображение можно преобразовать в такое отображение, которое сохраняет южный полюс фиксированным, используя вместо этого $z\; =\; H\; (1\; -\; u)\; 2.\; \{\backslash \; displaystyle\; z\; =\; \{\backslash \; frac\; \{H\; (1-u)\}\; \{2\}\}.\}$

Независимо от значений $(u,\; \varphi ,\; H)\; \{\backslash \; displaystyle\; (u,\; \backslash \; phi,\; H)\}$, якобиан этого сопоставления везде равен 1, показывая, что это действительно сопоставление равной площади на протяжении всей анимации. Это обобщенное сопоставление включает проекцию Ламберта как частный случай, когда $H\; =\; 0\; \{\backslash \; displaystyle\; H\; =\; 0\}$.

Приложение: это сопоставление может помочь в объяснении значения проекции Ламберта, показывая его «открывающимся» сфера на полюсе, превращая ее в диск без изменения области, заключенной в ячейках сетки.

На Викискладе есть материалы, связанные с азимутальной равновеликой проекцией Ламберта.

• Список картографических проекций
• Азимутальная эквидистантная проекция
• Европейская сетка
• Проекция молота

Источники

• Borradaile, Graham J. (2003). Статистика данных науки о Земле. Берлин: Springer-Verlag. ISBN 3-540-43603-0.
• ду Карму ; Манфредо П. (1976). Дифференциальная геометрия кривых и поверхностей. Энглвуд Клиффс, Нью-Джерси: Prentice Hall. ISBN 0-13-212589-7.
• Хоббс, Брюс Э., Минс, Уинтроп Д. и Уильямс, Пол Ф. (1976). Очерк структурной геологии. Нью-Йорк: John Wiley Sons, Inc. ISBN 0-471-40156-0. CS1 maint: несколько имен: список авторов (ссылка )
• Рамзи, Джон Г. (1967). Складывание и разрушение горных пород. Нью-Йорк: McGraw-Hill.
• Майкл Спивак (1999). Комплексное введение в дифференциальную геометрию. Хьюстон, Техас: Publish or Perish. ISBN 0-914098-70-5.

• Пояснения к преобразованию координат с помощью диаграмм
• Средства массовой информации, относящиеся к азимутальной равновеликой проекции Ламберта на Викимедиа Commons