Частица в одномерной решетке

В квантовой механике, то частица в одномерных решетках является проблемой, которая возникает в модели периодической кристаллической решетки. Потенциал вызван ионами в периодической структуре кристалла, создающими электромагнитное поле, поэтому электроны подвержены регулярному потенциалу внутри решетки. Это обобщение модели свободных электронов, которая предполагает нулевой потенциал внутри решетки.

• 1 Определение проблемы
• 2 Модель Кронига – Пенни
• 3 Ширина запрещенной зоны в модели Кронига – Пенни.
• 4 Модель Кронига – Пенни: альтернативное решение
• 5 См. Также
• 6 Ссылки
• 7 Внешние ссылки

Когда говорят о твердых материалах, в основном речь идет о кристаллах - периодических решетках. Здесь мы обсудим одномерную решетку положительных ионов. Предполагая, что расстояние между двумя ионами равно a, потенциал в решетке будет выглядеть примерно так:

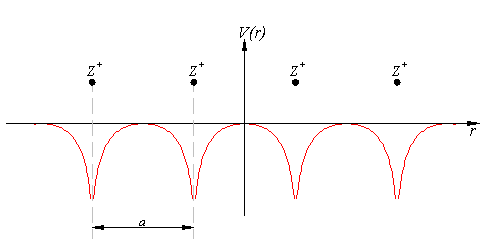
Математическое представление потенциала - периодическая функция с периодом а. Согласно теореме Блоха, решение волновой функции уравнения Шредингера при периодическом потенциале может быть записано как:

${\displaystyle \psi (x)=e^{ikx}u(x),}$

где u ( x) - периодическая функция, для которой u ( x + a) = u ( x). Фактор Блоха с показателем Флоке порождает зонную структуру энергетического спектра уравнения Шредингера с периодическим потенциалом, подобным потенциалу Кронига – Пенни, или функцией косинуса, как в уравнении Матье. ${\displaystyle k}$

При приближении к краям решетки возникают проблемы с граничным условием. Следовательно, мы можем представить ионную решетку в виде кольца, следуя граничным условиям Борна – фон Кармана. Если L - длина решетки, так что L ≫ a, то количество ионов в решетке настолько велико, что при рассмотрении одного иона его окружение почти линейно, а волновая функция электрона не изменяется. Итак, теперь вместо двух граничных условий мы получаем одно круговое граничное условие:

${\displaystyle \psi (0)=\psi (L).}$

Если N есть число ионов в решетке, то имеет место соотношение: = L. Замена в граничном условии и применение теоремы Блоха приведет к квантованию для k:

${\displaystyle \psi (0)=e^{ik\cdot 0}u(0)=e^{ikL}u(L)=\psi (L)}$

${\displaystyle u(0)=e^{ikL}u(L)=e^{ikL}u(Na)\to e^{ikL}=1}$

${\displaystyle \Rightarrow kL=2\pi n\to k={2\pi \over L}n\qquad \left(n=0,\pm 1,\cdots,\pm {N \over 2}\right).}$

Модель Кронига – Пенни (названная в честь Ральфа Кронига и Уильяма Пенни ) представляет собой простую идеализированную квантово-механическую систему, которая состоит из бесконечного периодического массива прямоугольных потенциальных барьеров.

Потенциальная функция аппроксимируется прямоугольным потенциалом:

Используя теорему Блоха, нам нужно найти решение только для одного периода, убедиться, что оно непрерывно и гладко, а также убедиться, что функция u ( x) также непрерывна и гладка.

Учитывая единый период потенциала: у нас здесь два региона. Мы решим для каждого независимо: Пусть E будет значением энергии над колодцем (Egt; 0)

${\displaystyle \mathrm {For} \quad 0lt;xlt;(a-b)}$ :

${\displaystyle {-\hbar ^{2} \over 2m}\psi _{xx}=E\psi }$

${\displaystyle \Rightarrow \psi =Ae^{i\alpha x}+A'e^{-i\alpha x}\quad \left(\alpha ^{2}={2mE \over \hbar ^{2}}\right)}$

${\displaystyle \mathrm {For} \quad -blt;xlt;0}$ :

${\displaystyle {-\hbar ^{2} \over 2m}\psi _{xx}=(E+V_{0})\psi }$

${\displaystyle \Rightarrow \psi =Be^{i\beta x}+B'e^{-i\beta x}\quad \left(\beta ^{2}={2m(E+V_{0}) \over \hbar ^{2}}\right).}$

Чтобы найти u ( x) в каждой области, нам нужно манипулировать волновой функцией электрона:

${\displaystyle \psi (0lt;xlt;a-b)=Ae^{i\alpha x}+A'e^{-i\alpha x}=e^{ikx}\cdot \left(Ae^{i(\alpha -k)x}+A'e^{-i(\alpha +k)x}\right)\,\!}$

${\displaystyle \Rightarrow u(0lt;xlt;a-b)=Ae^{i(\alpha -k)x}+A'e^{-i(\alpha +k)x}.\,\!}$

И таким же образом:

${\displaystyle u(-blt;xlt;0)=Be^{i(\beta -k)x}+B'e^{-i(\beta +k)x}.}$

Чтобы завершить решение, нам нужно убедиться, что функция вероятности является непрерывной и гладкой, то есть:

${\displaystyle \psi (0^{-})=\psi (0^{+})\qquad \psi '(0^{-})=\psi '(0^{+}).}$

И что u ( x) и u ′ ( x) периодичны:

${\displaystyle u(-b)=u(a-b)\qquad u'(-b)=u'(a-b).}$

Эти условия дают следующую матрицу:

${\displaystyle {\begin{pmatrix}1amp;1amp;-1amp;-1\\\alpha amp;-\alpha amp;-\beta amp;\beta \\e^{i(\alpha -k)(a-b)}amp;e^{-i(\alpha +k)(a-b)}amp;-e^{-i(\beta -k)b}amp;-e^{i(\beta +k)b}\\(\alpha -k)e^{i(\alpha -k)(a-b)}amp;-(\alpha +k)e^{-i(\alpha +k)(a-b)}amp;-(\beta -k)e^{-i(\beta -k)b}amp;(\beta +k)e^{i(\beta +k)b}\end{pmatrix}}{\begin{pmatrix}A\\A'\\B\\B'\end{pmatrix}}={\begin{pmatrix}0\\0\\0\\0\end{pmatrix}}.}$

Чтобы получить нетривиальное решение, определитель матрицы должен быть равен 0. Это приводит нас к следующему выражению:

${\displaystyle \cos(ka)=\cos(\beta b)\cos[\alpha (a-b)]-{\alpha ^{2}+\beta ^{2} \over 2\alpha \beta }\sin(\beta b)\sin[\alpha (a-b)].}$

Чтобы еще больше упростить выражение, мы выполняем следующие приближения:

${\displaystyle b\to 0;\quad V_{0}\to \infty ;\quad V_{0}b=\mathrm {constant} }$

${\displaystyle \Rightarrow \beta ^{2}b=\mathrm {constant} ;\quad \alpha ^{2}b\to 0}$

${\displaystyle \Rightarrow \beta b\to 0;\quad \sin(\beta b)\to \beta b;\quad \cos(\beta b)\to 1.}$

Выражение теперь будет:

${\displaystyle \cos(ka)=\cos(\alpha a)+P{\frac {\sin(\alpha a)}{\alpha a}},\qquad P={\frac {mV_{0}ba}{\hbar ^{2}}}.}$

Для значений энергии внутри ямы ( E  lt;0) получаем:

${\displaystyle \cos(ka)=\cos(\beta b)\cosh[\alpha (a-b)]-{\beta ^{2}-\alpha ^{2} \over 2\alpha \beta }\sin(\beta b)\sinh[\alpha (a-b)],}$

с и. ${\displaystyle \alpha ^{2}={2m|E| \over \hbar ^{2}}}$${\displaystyle \beta ^{2}={2m(V_{0}-|E|) \over \hbar ^{2}}}$

Следуя тем же приближениям, что и выше (), мы приходим к ${\displaystyle b\to 0;\,V_{0}\to \infty ;\,V_{0}b=\mathrm {constant} }$

${\displaystyle \cos(ka)=\cosh(\alpha a)+P{\frac {\sinh(\alpha a)}{\alpha a}}}$

по той же формуле для P, что и в предыдущем случае. ${\displaystyle \left(P={\frac {mV_{0}ba}{\hbar ^{2}}}\right)}$

Значение выражения, которому приравнивается cos (ka) в дисперсионном соотношении, с P = 1,5. Черные полосы обозначают области, для которых можно вычислить k.${\displaystyle \alpha a}$ Дисперсионное соотношение для модели Кронига – Пенни с P = 1.5.

В предыдущем абзаце единственными переменными, не определяемыми параметрами физической системы, являются энергия E и импульс кристалла k. Выбрав значение для E, можно вычислить правую часть, а затем вычислить k, взяв обе стороны. Таким образом, выражение приводит к дисперсионному соотношению. ${\displaystyle \arccos }$

Правая часть последнего выражения выше может иногда быть больше 1 или меньше -1, и в этом случае нет значения k, которое могло бы сделать уравнение истинным. Поскольку это означает, что существуют определенные значения E, для которых нет собственных функций уравнения Шредингера. Эти значения составляют ширину запрещенной зоны. ${\displaystyle \alpha a\propto {\sqrt {E}}}$

Таким образом, модель Кронига – Пенни является одним из простейших периодических потенциалов, демонстрирующих запрещенную зону.

Предлагается альтернативное лечение подобной проблемы. Здесь мы имеем дельта- периодический потенциал:

${\displaystyle V(x)=A\cdot \sum _{n=-\infty }^{\infty }\delta (x-n\cdot a).}$

A - некоторая константа, а a - постоянная решетки (расстояние между каждым узлом). Поскольку этот потенциал периодический, мы могли бы разложить его в ряд Фурье:

${\displaystyle V(x)=\sum _{K}{\tilde {V}}(K)\cdot e^{i\cdot K\cdot x},}$

куда

${\displaystyle {\tilde {V}}(K)={\frac {1}{a}}\int _{-a/2}^{a/2}dx\,V(x)\,e^{-i\cdot K\cdot x}={\frac {1}{a}}\int _{-a/2}^{a/2}dx\sum _{n=-\infty }^{\infty }A\cdot \delta (x-na)\,e^{-i\,K\,x}={\frac {A}{a}}}$.

Волновая функция, используя теорему Блоха, равна где - функция, периодическая в решетке, что означает, что мы также можем разложить ее в ряд Фурье: ${\displaystyle \psi _{k}(x)=e^{ikx}u_{k}(x)}$${\displaystyle u_{k}(x)}$

${\displaystyle u_{k}(x)=\sum _{K}{\tilde {u}}_{k}(K)e^{iKx}.}$

Таким образом, волновая функция:

${\displaystyle \psi _{k}(x)=\sum _{K}{\tilde {u}}_{k}(K)\,e^{i(k+K)x}.}$

Подставляя это в уравнение Шредингера, мы получаем:

${\displaystyle \left[{\frac {\hbar ^{2}(k+K)^{2}}{2m}}-E_{k}\right]\cdot {\tilde {u}}_{k}(K)+\sum _{K'}{\tilde {V}}(K-K')\,{\tilde {u}}_{k}(K')=0}$

или скорее:

${\displaystyle \left[{\frac {\hbar ^{2}(k+K)^{2}}{2m}}-E_{k}\right]\cdot {\tilde {u}}_{k}(K)+{\frac {A}{a}}\sum _{K'}{\tilde {u}}_{k}(K')=0}$

Теперь мы понимаем, что:

${\displaystyle u_{k}(0)=\sum _{K'}{\tilde {u}}_{k}(K')}$

Подключите это к уравнению Шредингера:

${\displaystyle \left[{\frac {\hbar ^{2}(k+K)^{2}}{2m}}-E_{k}\right]\cdot {\tilde {u}}_{k}(K)+{\frac {A}{a}}u_{k}(0)=0}$

Решая это, мы получаем: ${\displaystyle {\tilde {u}}_{k}(K)}$

${\displaystyle {\tilde {u}}_{k}(K)={\frac {{\frac {2m}{\hbar ^{2}}}{\frac {A}{a}}f(k)}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}={\frac {{\frac {2m}{\hbar ^{2}}}{\frac {A}{a}}}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}\,u_{k}(0)}$

Суммируя это последнее уравнение по всем значениям K, получаем:

${\displaystyle \sum _{K}{\tilde {u}}_{k}(K)=\sum _{K}{\frac {{\frac {2m}{\hbar ^{2}}}{\frac {A}{a}}}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}\,u_{k}(0)}$

Или:

${\displaystyle u_{k}(0)=\sum _{K}{\frac {{\frac {2m}{\hbar ^{2}}}{\frac {A}{a}}}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}\,u_{k}(0)}$

Удобно отменяем ауты и получаем: ${\displaystyle u_{k}(0)}$

${\displaystyle 1=\sum _{K}{\frac {{\frac {2m}{\hbar ^{2}}}{\frac {A}{a}}}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}}$

Или:

${\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}=\sum _{K}{\frac {1}{{\frac {2mE_{k}}{\hbar ^{2}}}-(k+K)^{2}}}}$

Чтобы избавить себя от ненужных усилий с обозначениями, мы определяем новую переменную:

${\displaystyle \alpha ^{2}:={\frac {2mE_{k}}{\hbar ^{2}}}}$

и, наконец, наше выражение:

${\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}=\sum _{K}{\frac {1}{\alpha ^{2}-(k+K)^{2}}}}$

Теперь K является вектором обратной решетки, что означает, что сумма по K на самом деле является суммой целых кратных: ${\displaystyle {\frac {2\pi }{a}}}$

${\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}=\sum _{n=-\infty }^{\infty }{\frac {1}{\alpha ^{2}-(k+{\frac {2\pi n}{a}})^{2}}}}$

Мы можем немного подтасовать это выражение, чтобы сделать его более наглядным (используйте разложение на частичную дробь ):

${\displaystyle {\begin{aligned}{\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}amp;=\sum _{n=-\infty }^{\infty }{\frac {1}{\alpha ^{2}-(k+{\frac {2\pi n}{a}})^{2}}}\\amp;=-{\frac {1}{2\alpha }}\sum _{n=-\infty }^{\infty }\left[{\frac {1}{(k+{\frac {2\pi n}{a}})-\alpha }}-{\frac {1}{(k+{\frac {2\pi n}{a}})+\alpha }}\right]\\amp;=-{\frac {a}{4\alpha }}\sum _{n=-\infty }^{\infty }\left[{\frac {1}{\pi n+{\frac {ka}{2}}-{\frac {\alpha a}{2}}}}-{\frac {1}{\pi n+{\frac {ka}{2}}+{\frac {\alpha a}{2}}}}\right]\\amp;=-{\frac {a}{4\alpha }}\left[\sum _{n=-\infty }^{\infty }{\frac {1}{\pi n+{\frac {ka}{2}}-{\frac {\alpha a}{2}}}}-\sum _{n=-\infty }^{\infty }{\frac {1}{\pi n+{\frac {ka}{2}}+{\frac {\alpha a}{2}}}}\right]\end{aligned}}}$

Если мы используем красивую идентичность суммы функции котангенса ( уравнение 18 ), которая говорит:

${\displaystyle \cot(x)=\sum _{n=-\infty }^{\infty }{\frac {1}{2\pi n+2x}}-{\frac {1}{2\pi n-2x}}}$

и вставьте его в наше выражение, мы получим:

${\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {a}{A}}=-{\frac {a}{4\alpha }}\left[\cot \left({\tfrac {ka}{2}}-{\tfrac {\alpha a}{2}}\right)-\cot \left({\tfrac {ka}{2}}+{\tfrac {\alpha a}{2}}\right)\right]}$

Мы используем сумму cot, а затем произведение sin (которое является частью формулы для суммы cot), чтобы получить:

${\displaystyle \cos(ka)=\cos(\alpha a)+{\frac {mA}{\hbar ^{2}\alpha }}\sin(\alpha a)}$

Это уравнение показывает связь между энергией (через α) и волновым вектором k, и, как вы можете видеть, поскольку левая часть уравнения может находиться в диапазоне только от -1 до 1, то есть некоторые ограничения на значения что α (и, следовательно, энергия) может принимать, то есть в некоторых диапазонах значений энергии нет решения в соответствии с этим уравнением, и, таким образом, система не будет иметь этих энергий: энергетических зазоров. Это так называемые запрещенные зоны, которые, как можно показать, существуют в любой форме периодического потенциала (не только дельта-барьеры или квадратные барьеры).

Для другого и подробного расчета формулы зазора (т.е. для зазора между зонами) и расщепления уровней собственных значений одномерного уравнения Шредингера см. Müller-Kirsten. Соответствующие результаты для косинусного потенциала (уравнение Матье) также подробно представлены в этой ссылке.

• Модель свободных электронов
• Приближение пустой решетки
• Модель почти свободных электронов
• Кристальная структура
• Функция Матье

• « Модель Кронига – Пенни » Майкла Краучера, интерактивное вычисление 1d периодической потенциальной зонной структуры с использованием Mathematica, из проекта Wolfram Demonstrations Project.