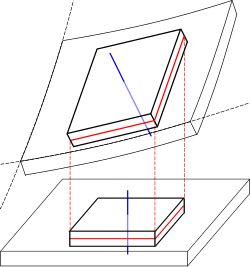
Деформация тонкой пластины с выделением смещения, средней поверхности (красный цвет) и нормали к средней поверхности (синий)
Теория пластин Кирхгофа – Лява представляет собой двумерную математическую модель, которая используется для определения напряжений и деформаций. в тонких пластинах, подверженных воздействию сил и моментов. Эта теория является расширением теории пучка Эйлера-Бернулли и была разработана в 1888 году Лавом с использованием предположений, предложенных Кирхгофом. Теория предполагает, что плоскость средней поверхности может использоваться для представления трехмерной пластины в двухмерной форме.
Следующие кинематические допущения, которые сделаны в этой теории:
- прямые линии, нормальные к средней поверхности, остаются прямыми после деформации
- прямые линии, нормальные к средней поверхности, остаются нормальными к средняя поверхность после деформации
- толщина пластины не изменяется во время деформации.
Содержание
- 1 Предполагаемое поле смещения
- 2 Квазистатические пластины Кирхгофа-Лява
- 2.1 Деформация-смещение соотношения
- 2.2 Уравнения равновесия
- 2.3 Граничные условия
- 2.4 Определяющие соотношения
- 2.5 Малые деформации и умеренные вращения
- 3 Изотропные квазистатические пластины Кирхгофа-Лява
- 3.1 Чистый изгиб
- 3.2 Изгиб под поперечная нагрузка
- 3.3 Цилиндрический изгиб
- 4 Динамика пластин Кирхгофа-Лява
- 4.1 Управляющие уравнения
- 4.2 Изотропные пластины
- 5 Ссылки
- 6 См. также
Предполагаемое поле смещения
Пусть вектор положения точки в недеформированной пластине будет  . Тогда
. Тогда

Векторы  образуют декартово базис с началом на средней поверхности пластины,
образуют декартово базис с началом на средней поверхности пластины,  и
и  - декартовы координаты на средней поверхности недеформированной пластины, а
- декартовы координаты на средней поверхности недеформированной пластины, а  - координата направления толщины.
- координата направления толщины.
Пусть смещение точки на пластине будет  . Тогда
. Тогда

Это смещение может быть разложено на векторную сумму смещения средней поверхности  и смещения вне плоскости
и смещения вне плоскости  в направлении
в направлении  . Мы можем записать смещение средней поверхности в плоскости как
. Мы можем записать смещение средней поверхности в плоскости как

Обратите внимание, что индекс  принимает значения 1 и 2, но не 3.
принимает значения 1 и 2, но не 3.
Тогда из гипотезы Кирхгофа следует, что

Если  - это углы поворота нормально к средней поверхности, тогда в теории Кирхгофа-Лява
- это углы поворота нормально к средней поверхности, тогда в теории Кирхгофа-Лява

Обратите внимание, что мы можем думать о выражении для  как о расширении серии Тейлора первого порядка для смещения вокруг средняя поверхность.
как о расширении серии Тейлора первого порядка для смещения вокруг средняя поверхность.
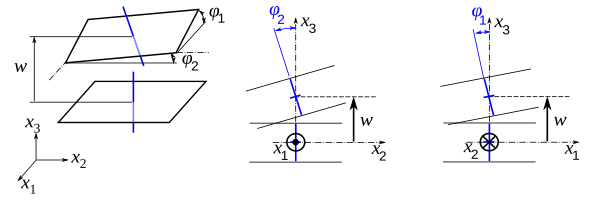
Смещение средней поверхности (слева) и нормальной (справа)
Квазистатические пластины Кирхгофа-Лява
Первоначальная теория, разработанная Лавом, действительна для бесконечно малых деформаций и вращений. фон Карман расширил эту теорию на ситуации, в которых можно было ожидать умеренных вращений.
Соотношение деформация-смещение
Для ситуации, когда деформации в пластине бесконечно малы, а вращение нормалей средней поверхности меньше 10 °, деформация-смещение отношения следующие:

где  as
as  .
.
Используя кинематические допущения, мы имеем

Следовательно, ненулевые деформации только в плоскостях.
Уравнения равновесия
Уравнения равновесия для пластины могут быть выведены из принципа виртуальной работы. Для тонкой пластины под квазистатической поперечной нагрузкой  эти уравнения имеют вид
эти уравнения имеют вид

где толщина пластины составляет  . В индексных обозначениях
. В индексных обозначениях

где  - напряжения.
- напряжения.
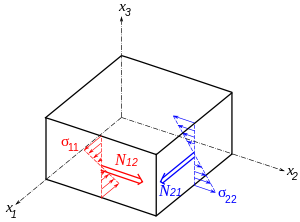 Изгибающие моменты и нормальные напряжения Изгибающие моменты и нормальные напряжения |  Моменты и касательные напряжения Моменты и касательные напряжения |
| Вывод уравнений равновесия для малых вращений |
|---|
Для ситуации, когда деформации и вращения пластины малы, виртуальная внутренняя энергия определяется выражением ![{\ begin {align} \ delta U = \ int _ {{\ Omega ^ { 0}}} \ int _ {{- h}} ^ {h} {\ boldsymbol {\ sigma}}: \ delta {\ boldsymbol {\ epsilon}} ~ dx_ {3} ~ d \ Omega = \ int _ { {\ Omega ^ {0}}} \ int _ {{- h}} ^ {h} \ sigma _ {{\ alpha \ beta}} ~ \ delta \ varepsilon _ {{\ alpha \ beta}} ~ dx_ { 3} ~ d \ Omega \\ = \ int _ {{\ Omega ^ {0}}} \ int _ {{- h}} ^ {h} \ left [{\ frac {1} {2}} ~ \ sigma _ {{\ alpha \ beta}} ~ (\ delta u _ {{\ alpha, \ beta}} ^ {0} + \ delta u _ {{\ beta, \ alpha}} ^ {0}) - x_ { 3} ~ \ sigma _ {{\ alpha \ beta}} ~ \ delta w _ {{, \ alpha \ beta}} ^ {0} \ right] ~ dx_ {3} ~ d \ Omega \\ = \ int _ {{\ Omega ^ {0}}} \ left [{\ frac {1} {2}} ~ N _ {{\ alpha \ beta}} ~ (\ delta u _ {{\ alpha, \ beta}} ^ {0 } + \ delta u _ {{\ beta, \ alpha}} ^ {0}) - M _ {{\ alpha \ beta}} ~ \ delta w _ {{, \ alpha \ beta}} ^ {0} \ right] ~ d \ Omega \ end {align}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a31f90cfd37649392fb2f57ac5292c6a657e6da9)
где толщина пластины равно  , а результирующие напряжения и результирующие моменты напряжений определены как , а результирующие напряжения и результирующие моменты напряжений определены как 
Интеграция по частей приводит к ![{\ begin {align} \ delta U = \ int _ {{\ Omega ^ {0}}} \ left [- {\ frac {1} {2}} ~ (N _ {{\ alpha \ beta, \ beta}} ~ \ delta u _ {{\ alpha}} ^ { 0} + N _ {{\ alpha \ beta, \ alpha}} ~ \ delta u _ {{\ beta}} ^ {0}) + M _ {{\ alpha \ beta, \ beta}} ~ \ delta w _ {{, \ alpha}} ^ {0} \ right] ~ d \ Omega \\ + \ int _ {{\ Gamma ^ {0}}} \ left [{\ frac {1} {2}} ~ (n _ {\ beta} ~ N _ {{\ alpha \ beta}} ~ \ delta u _ {\ alpha} ^ {0} + n _ {\ alpha} ~ N _ {{\ alpha \ beta}} ~ \ delta u _ {{\ beta}} ^ {0}) - n _ {\ beta} ~ M _ {{\ alpha \ beta}} ~ \ delta w _ {{, \ alpha}} ^ {0} \ right] ~ d \ Gamma \ end {выравнивается}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a383a0911e113ebff8ae10a89a1b5db8c8dd3d61)
Симметрия тензора напряжений означает, что  . Следовательно, . Следовательно, ![\ delta U = \ int _ {{\ Omega ^ {0}}} \ l eft [-N _ {{\ alpha \ beta, \ alpha}} ~ \ delta u _ {{\ beta}} ^ {0} + M _ {{\ alpha \ beta, \ beta}} ~ \ delta w _ {{, \ alpha}} ^ {0} \ right] ~ d \ Omega + \ int _ {{\ Gamma ^ {0}}} \ left [n _ {\ alpha} ~ N _ {{\ alpha \ beta}} ~ \ delta u_ {{\ beta}} ^ {0} -n _ {\ beta} ~ M _ {\ alpha \ beta}} ~ \ delta w _ {{, \ alpha}} ^ {0} \ right] ~ d \ Gamma](https://wikimedia.org/api/rest_v1/media/math/render/svg/77e91656378bc8d97107821d5914d36d7072bde0)
Другое интегрирование по частям дает ![\ delta U = \ int _ {{\ Omega ^ {0}}} \ left [-N _ {{\ alpha \ beta, \ alpha}} ~ \ delta u _ {{\ beta}} ^ {0} -M _ {{\ alpha \ beta, \ beta \ alpha}} ~ \ delta w ^ {0} \ right] ~ d \ Omega + \ int _ {{\ Gamma ^ {0}}} \ left [n _ {\ alpha} ~ N _ {{\ alpha \ beta }} ~ \ delta u _ {{\ beta}} ^ {0} + n _ {\ alpha} ~ M _ {{\ alpha \ beta, \ beta}} ~ \ delta w ^ {0} -n _ {\ beta} ~ M _ {{\ alpha \ beta}} ~ \ delta w _ {{, \ альфа}} ^ {0} \ right] ~ d \ Gamma](https://wikimedia.org/api/rest_v1/media/math/render/svg/e944b4bbf4358edc5ed737e010e6e7b6948c49c4)
Для случая, когда Если нет предписанных внешних сил, принцип виртуальной работы подразумевает, что  . Уравнения равновесия для пластины тогда задаются следующим образом: . Уравнения равновесия для пластины тогда задаются следующим образом: 
Если плита нагружена внешней распределенной нагрузкой  , которая перпендикулярна средней поверхности и направлена в положительном направлении , которая перпендикулярна средней поверхности и направлена в положительном направлении  , внешняя виртуальная работа из-за нагрузки равно , внешняя виртуальная работа из-за нагрузки равно 
Затем принцип виртуальной работы приводит к уравнениям равновесия 
|
Граничные условия
Граница условия, необходимые для решения уравнений равновесия теории пластин, могут быть получены из граничных членов в принципе виртуальная работа. В отсутствие внешних сил на границе граничные условия следующие:

Обратите внимание, что величина  - эффективная сила сдвига.
- эффективная сила сдвига.
Определяющие соотношения
Соотношения между напряжением и деформацией для линейной упругой пластины Кирхгофа определяются как

Поскольку  и
и  не фигурируют в уравнениях равновесия, неявно предполагается, что эти величины не влияют на баланс импульса и ими пренебрегают. Остальные соотношения напряжение-деформация в матричной форме могут быть записаны как
не фигурируют в уравнениях равновесия, неявно предполагается, что эти величины не влияют на баланс импульса и ими пренебрегают. Остальные соотношения напряжение-деформация в матричной форме могут быть записаны как

Тогда

и

жесткости на растяжение - это величины

жесткость на изгиб (также называемая жесткостью на изгиб ) - величины

Основные предположения Кирхгофа-Лява приводят к нулевым поперечным силам. В результате уравнения равновесия пластины должны использоваться для определения поперечных сил в тонких пластинах Кирхгофа-Лява. Для изотропных пластин эти уравнения приводят к

В качестве альтернативы, эти поперечные силы могут быть выражены как

где

Небольшие деформации и умеренные повороты
Если вращение нормалей на средняя поверхность находится в диапазоне от 10  до 15
до 15  , соотношения деформация-перемещение можно аппроксимировать как
, соотношения деформация-перемещение можно аппроксимировать как

Тогда кинематические предположения Кирхгофа- Теория Лява приводит к классической теории пластин с фон Карманом деформациями

Эта теория нелинейна из-за квадратичных членов в соотношениях деформация-смещение.
Если соотношения деформация-смещение принимают форму фон Кармана, уравнения равновесия могут быть выражены как
![{\ begin {align} N _ {{\ alpha \ beta, \ alpha}} = 0 \\ M _ {{ \ alpha \ beta, \ alpha \ beta}} + [N _ {{\ alpha \ beta}} ~ w _ {{, \ beta}} ^ {0}] _ {{, \ alpha}} - q = 0 \ end {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/805c3eb5885064aa33be7d31e0e054995853f47a)
Изотропные квазистатические пластины Кирхгофа-Лява
Для изотропных и однородной пластине, отношения напряжение-деформация следующие:

где  - коэффициент Пуассона и
- коэффициент Пуассона и  - это модуль Юнга. Моменты, соответствующие этим напряжениям, равны
- это модуль Юнга. Моменты, соответствующие этим напряжениям, равны

В развернутом виде,

где ![D = 2h ^ {3} E / [3 (1- \ nu ^ {2})] = H ^ {3} E / [12 (1- \ nu ^ {2})]](https://wikimedia.org/api/rest_v1/media/math/render/svg/76681f1dbad8aed514809b36dd0dc21d8cd099f3) для пластин толщиной
для пластин толщиной  . Используя соотношения напряжения и деформации для пластин, мы можем показать, что напряжения и моменты связаны соотношением
. Используя соотношения напряжения и деформации для пластин, мы можем показать, что напряжения и моменты связаны соотношением

Вверху пластины, где  , напряжения
, напряжения

Чистый изгиб
Для изотропной и однородной пластины при чистом изгибе определяющие уравнения сводятся к

Здесь мы предположили, что смещения в плоскости не меняются в зависимости от  и
и  . В индексной записи
. В индексной записи

и в прямой записи

которое известно как бигармоническое уравнение. Изгибающие моменты определяются как

| Вывод уравнений равновесия для чистого изгиба |
|---|
Для изотропной однородной пластины при чистом изгибе определяющие уравнения следующие: 
и отношения напряжение-деформация равны 
Тогда 
и 
Дифференциация дает 
и 
Включение в основные уравнения приводит к 
Поскольку порядок дифференцирования не имеет значения, мы имеем  , ,  и и  . Следовательно, . Следовательно, 
В прямой тензорной записи основное уравнение пластины: 
где мы предположили, что смещения  постоянны. постоянны. |
Изгиб под поперечной нагрузкой
Если к пластине применяется распределенная поперечная нагрузка  , определяющее уравнение равно
, определяющее уравнение равно  . Следуя процедуре, описанной в предыдущем разделе, мы получаем
. Следуя процедуре, описанной в предыдущем разделе, мы получаем

В прямоугольных декартовых координатах основное уравнение:

и в цилиндрических координатах принимает вид
![\ frac {1} {r} \ cfrac {d} {dr} \ left [r \ cfrac {d} {dr} \ left \ {\ frac { 1} {r} \ cfrac {d} {dr} \ left (r \ cfrac {dw} {dr} \ right) \ right \} \ right] = - \ frac {q} {D} \,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8083e6e16a9118c0afe8bd3c7e1fe841e17334)
Решения этого уравнения для различных геометрических форм и граничных условий можно найти в статье о изгибе пластин.
| Вывод уравнений равновесия для поперечного нагружения |
|---|
Для поперечно нагруженной пластины без осевых деформаций управляющее уравнение имеет вид 
, где  - распределенная поперечная нагрузка (на единицу площади). Подстановка выражений для производных от - распределенная поперечная нагрузка (на единицу площади). Подстановка выражений для производных от  в основное уравнение дает в основное уравнение дает ![- {\ cfrac {2h ^ { 3} E} {3 (1- \ nu ^ {2})}} \ left [w _ {{, 1111}} ^ {0} +2 \, w _ {{, 1212}} ^ {0} + w_ { {, 2222}} ^ {0} \ right] = q \,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/417364393d9d4a16c51bb93210063b9d70cfd569)
Заметим, что жесткость на изгиб - это величина 
мы можем записать основное уравнение в виде

В цилиндрических координатах  , , 
Для симметрично нагруженных круглых пластин  , и мы имеем , и мы имеем 
|
Цилиндрический изгиб
При определенных условиях нагружения плоская пластина может изгибаться, принимая форму поверхности цилиндра. Этот тип гибки называется цилиндрической гибкой и представляет собой особую ситуацию, когда  . В этом случае
. В этом случае

и

и определяющие уравнения принимают вид

Dynamics of Kirchhoff-Love plates
The dynamic theory of thin plates determines the propagation of waves in the plates, and the study of standing waves and vibration modes.
Governing equations
The governing equations for the dynamics of a Kirchhoff-Love plate are

where, for a plate with density  ,
,

and

| Derivation of equations governing the dynamics of Kirchhoff-Love plates |
|---|
The total kinetic energy of the plate is given by ![К = \ int _ {0} ^ {T} \ int _ {{\ Om ega ^ {0}}} \ int _ {{- h}} ^ {h} {\ cfrac {\ rho} {2}} \ left [\ left ({\ frac {\ partial u_ {1}} {\ частичный t}} \ right) ^ {2} + \ left ({\ frac {\ partial u_ {2}} {\ partial t}} \ right) ^ {2} + \ left ({\ frac {\ partial u_ {3}} {\ partial t}} \ right) ^ {2} \ right] ~ {\ mathrm {d}} x_ {3} ~ {\ mathrm {d}} A ~ {\ mathrm {d}} t](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1c288ee3df8a9785bc05065e597fb3ab5a0cda0)
Therefore, the variation in kinetic energy is ![\ delta K = \ int _ {0} ^ {T} \ int _ {{\ Omega ^ {0}}} \ int _ {{- h}} ^ {h} {\ cfrac {\ rho} {2}} \ left [2 \ left ({\ frac {\ partial u_ {1}} {\ partial t}} \ right) \ left ({\ frac {\ partial \ delta u_ {1}} {\ partial t}} \ right) +2 \ left ({\ frac {\ partial u_ {2}} {\ partial t}} \ right) \ left ({\ frac {\ partial \ delta u_ {2}} {\ partial t}} \ right) +2 \ left ({\ frac {\ partial u_ {3}} {\ partial t}} \ right) \ left ({\ frac {\ partial \ delta u_ {3}} {\ partial t}} \ right) \ right] ~ {\ mathrm {d}} x_ {3} ~ {\ mathrm {d}} A ~ {\ mathrm {d}} t](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc9767e81d5a99dd50bc1238897bc05c44efdd8)
We use the following notation in the rest of this section. 
Then 
For a Kirchhof-Love plate 
Hence, ![{\ begin {align} \ delta K = \ int _ {0} ^ {T} \ int _ {{\ Omega ^ {0}}} \ int _ {{- h}} ^ {h} \ rho \ left [\ left ({\ dot {u }} _ {\ alpha} ^ {0} -x_ {3} ~ {\ dot {w}} _ {{, \ alpha}} ^ {0} \ right) ~ \ left (\ delta {\ dot {u }} _ {\ alpha} ^ {0} -x_ {3} ~ \ delta {\ dot {w}} _ {{, \ alpha}} ^ {0} \ right) + {\ dot {w}} ^ {0} ~ \ delta {\ dot {w}} ^ {0} \ right] ~ {\ mathrm {d}} x_ {3} ~ {\ mathrm {d}} A ~ {\ mathrm {d}} t \\ = \ int _ {0} ^ {T} \ int _ {{\ Omega ^ {0}}} \ int _ {{- h}} ^ {h} \ rho \ left ({\ dot {u }} _ {\ alpha} ^ {0} ~ \ delta {\ do t {u}} _ {\ alpha} ^ {0} -x_ {3} ~ {\ dot {w}} _ {{, \ alpha}} ^ {0} ~ \ delta {\ dot {u}} _ {\ alpha} ^ {0} -x_ {3} ~ {\ dot {u}} _ {\ alpha} ^ {0} ~ \ delta {\ dot {w}} _ {{, \ alpha}} ^ { 0} + x_ {3} ^ {2} ~ {\ dot {w}} _ {{, \ alpha}} ^ {0} ~ \ delta {\ dot {w}} _ {{, \ alpha}} ^ {0} + {\ dot {w}} ^ {0} ~ \ delta {\ dot {w}} ^ {0} \ right) ~ {\ mathrm {d}} x_ {3} ~ {\ mathrm {d }} A ~ {\ mathrm {d}} t \ end {align}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f11678997d40383ba8de7415769b832adbd0b8c)
Define, for constant  through the thickness of the plate, through the thickness of the plate, 
Then ![\ дельта K = \ int _ {0} ^ {T} \ int _ {{\ Omega ^ {0}}} \ left [J_ {1} \ left ({\ dot {u}} _ {\ alpha} ^ { 0} ~ \ delta {\ dot {u}} _ {\ alpha} ^ {0} + {\ dot {w}} ^ {0} ~ \ delta {\ dot {w}} ^ {0} \ right) + J_ {3} ~ {\ dot {w}} _ {{, \ alpha}} ^ {0} ~ \ delta {\ dot {w}} _ {{, \ alpha}} ^ {0} \ right] ~ {\ mathrm {d}} A ~ {\ mathrm {d}} t](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d016ce8f7f0266d9ea351c79ce06f24e150c7d7)
Интегрирование по частям, ![\ delta K = \ int _ {{\ Omega ^ {0}} } \ left [\ int _ {0} ^ {T} \ left \ {- J_ {1} \ left ({\ ddot {u}} _ {{\ alpha}} ^ {0} ~ \ delta u _ {\ альфа} ^ {0} + {\ ddot {w}} ^ {0} ~ \ delta w ^ {0} \ right) -J_ {3} ~ {\ ddot {w}} _ {{, \ alpha}} ^ {0} ~ \ delta w _ {, \ alpha}} ^ {0} \ right \} ~ {\ mathrm {d}} t + \ left | J_ {1} \ left ({\ dot {u}} _ {{\ alpha}} ^ {0} ~ \ delta u _ {\ alpha} ^ {0} + {\ dot {w}} ^ {0} ~ \ delta w ^ {0} \ right) + J_ {3} ~ {\ dot {w}} _ {{, \ alpha}} ^ {0} ~ \ delta w _ {{, \ alpha}} ^ {0} \ right | _ {0} ^ {T} \ right] ~ {\ mathrm {d}} A](https://wikimedia.org/api/rest_v1/media/math/render/svg/74b06ceac1f8b3b67d3b47225d09c6560abc1451)
Варианты  и и  равны нулю при равны нулю при  и и  . Следовательно, после переключения последовательности интегрирования имеем . Следовательно, после переключения последовательности интегрирования имеем ![\delta K=-\int _{0}^{T}\left\{\int _{{\Omega ^{0}}}\left[J_{1}\left({\ddot {u}}_{{\alpha }}^{0}~\delta u_{\alpha }^{0}+{\ddot {w}}^{0}~\delta w^{0}\right)+J_{3}~{\ddot {w}}_{{,\alpha }}^{0}~\delta w_{{,\alpha }}^{0}\right]~{\mathrm {d}}A\right\}~{\mathrm {d}}t+\left|\int _{{\Omega ^{0}}}J_{3}~{\dot {w}}_{{,\alpha }}^{0}~\delta w_{{,\alpha }}^{0}{\mathrm {d}}A\right|_{0}^{T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/776c5e9fbb35fd7fc9c0bc7573edd812b9fe390b)
Интегрирование по частям по средней поверхности дает ![{\ begin {align} \ delta K = - \ int _ {0} ^ {T} \ left \ {\ int _ {{\ Omega ^ {0}}} \ left [J_ {1} \ left ({\ ddot {u}} _ {{\ alpha}} ^ {0} ~ \ delta u _ {\ alpha} ^ {0} + {\ ddot { w}} ^ {0} ~ \ delta w ^ {0} \ right) -J_ {3} ~ {\ ddot {w}} _ {, \ alpha \ alpha}} ^ {0} ~ \ delta w ^ {0} \ right] ~ {\ mathrm {d}} A + \ int _ {{\ Gamma ^ {0}}} J_ {3} ~ n _ {\ alpha} ~ {\ ddot {w}} _ {, \ alpha}} ^ {0} ~ \ delta w ^ {0} ~ {\ mathrm {d}} s \ right \} ~ {\ mathrm {d}} t \\ \ qquad - \ left | \ int _ {{\ Omega ^ {0}}} J_ {3} ~ {\ dot {w}} _ {{, \ alpha \ alpha}} ^ {0} ~ \ delta w ^ {0} ~ {\ mathrm {d }} A- \ int _ {{\ Gamma ^ {0}}} J_ {3} ~ {\ dot {w}} _ {{, \ alpha}} ^ {0} ~ \ delta w ^ {0} ~ {\ mathrm {d}} s \ right | _ {0} ^ {T} \ end {align}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0994fb48ef584ebbe117df459f57c2aafe22484)
Опять же, так как вначале варианты равны нулю и в конце рассматриваемого интервала времени имеем ![\ delta K = - \ int _ {0} ^ {T} \ left \ {\ int _ {{\ Omega ^ {0}}} \ left [J_ {1} \ left ({\ ddot {u}} _ {{\ alpha}} ^ {0} ~ \ delta u _ {\ alpha} ^ { 0} + {\ ddot {w}} ^ {0} ~ \ delta w ^ {0} \ right) -J_ {3} ~ {\ ddot {w}} _ {{, \ alpha \ alpha}} ^ { 0} ~ \ delta w ^ {0} \ right] ~ {\ mathrm {d}} A + \ int _ {{\ Gamma ^ {0}}} J_ {3} ~ n _ {\ alpha} ~ {\ ddot { w}} _ {{, \ alpha}} ^ {0} ~ \ delta w ^ {0} ~ {\ mathrm {d}} s \ right \} ~ {\ mathrm {d}} t](https://wikimedia.org/api/rest_v1/media/math/render/svg/294068d98e0f0f77c313f3aaf323136a08a520b0)
Для динамического случая изменение внутренней энергии определяется как ![\ delta U = - \ int _ {0} ^ {T} \ left \ {\ int _ {{\ Omega ^ {0}}} \ left [N _ {{\ alpha \ beta, \ alpha}} ~ \ delta u_ { {\ beta}} ^ {0} + M _ {{\ alpha \ beta, \ beta \ alpha}} ~ \ delta w ^ {0} \ right] ~ {\ mathrm {d}} A- \ int _ {{ \ Gamma ^ {0}}} \ left [n _ {\ alpha} ~ N _ {{\ alpha \ beta}} ~ \ delta u _ {{\ beta}} ^ {0} + n _ {\ alpha} ~ M _ {{ \ alpha \ beta, \ beta}} ~ \ delta w ^ {0} -n _ {\ beta} ~ M _ {{\ alpha \ beta}} ~ \ delta w _ {{, \ alpha}} ^ {0} \ right ] ~ {\ mathrm {d}} s \ right \} {\ mathrm {d}} t](https://wikimedia.org/api/rest_v1/media/math/render/svg/41fec6c49872524d2a22b9fe51e5a1efaaa86e14)
Интегрирование по частям и обращение к нулю вариации на границе средней поверхности дает ![\ delta U = - \ int _ {0} ^ {T} \ left \ {\ int _ {{\ Omega ^ {0}}} \ left [N _ {{\ alpha \ beta, \ alpha}} ~ \ delta u _ {{\ beta}} ^ {0} + M _ {{\ alpha \ beta, \ beta \ alpha}} ~ \ delta w ^ {0} \ right] ~ {\ mathrm {d}} A- \ int _ {{\ Gamma ^ {0}}} \ left [n _ {\ alpha} ~ N _ {{\ alpha \ beta }} ~ \ delta u _ {{\ beta}} ^ {0} + n _ {\ alpha} ~ M _ {{\ alpha \ beta, \ beta}} ~ \ delta w ^ {0} + n _ {\ beta} ~ M _ {{\ alpha \ beta, \ alpha} } ~ \ delta w ^ {0} \ right] ~ {\ mathrm {d}} s \ right \} {\ mathrm {d}} t](https://wikimedia.org/api/rest_v1/media/math/render/svg/5298d7974d399e1e6df1be946a9af380491a688e)
Если есть внешний распределенная сила  , действующая перпендикулярно поверхности пластины, выполненная виртуальная внешняя работа равна , действующая перпендикулярно поверхности пластины, выполненная виртуальная внешняя работа равна ![\delta V_{{{\mathrm {ext}}}}=\int _{0}^{T}\left[\int _{{\Omega ^{0}}}q(x,t)~\delta w^{0}~{\mathrm {d}}A\right]{\mathrm {d}}t](https://wikimedia.org/api/rest_v1/media/math/render/svg/d88f260cad14333af5ce1e7bf7f638b03b930ae4)
Из принципа виртуальной работы  . Следовательно, основные уравнения баланса для пластины: . Следовательно, основные уравнения баланса для пластины: 
|
Решения этих уравнений для некоторых частных случаев можно найти в статье о колебаниях пластин. На рисунках ниже показаны некоторые колебательные моды круглой пластины.
режим k = 0, p = 1

режим k = 0, p = 2
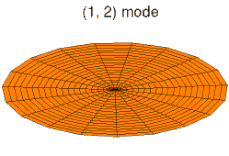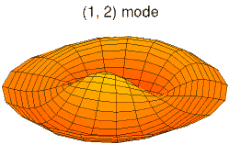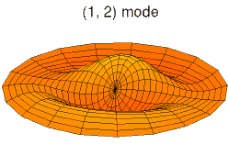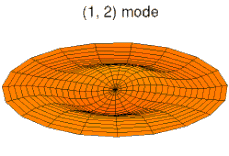
режим k = 1, p = 2
изотропные пластины
Основные уравнения значительно упрощаются для изотропные и однородные пластины, для которых плоскими деформациями можно пренебречь. В этом случае остается одно уравнение следующего вида (в прямоугольных декартовых координатах):

где  - жесткость пластины на изгиб. Для однородной пластины толщиной
- жесткость пластины на изгиб. Для однородной пластины толщиной  ,
,

В прямой записи

Для свободных колебаний основное уравнение принимает вид

| Вывод динамических управляющих уравнений для изотропных уравнений Кирхгофа- Пластины Лява |
|---|
Для изотропной и однородной пластины отношения напряжение-деформация следующие: 
где  - деформации в плоскости. Соотношения деформация-смещение для пластин Кирхгофа-Лява следующие: - деформации в плоскости. Соотношения деформация-смещение для пластин Кирхгофа-Лява следующие: 
Следовательно, результирующие моменты, соответствующие этим напряжениям, равны 
Основное уравнение для изотропной и однородная пластина одинаковой толщины  при отсутствии смещений в плоскости при отсутствии смещений в плоскости 
Дифференцирование выражений для результирующих моментов дает нам 
Подстановка в основные уравнения приводит к 
Поскольку порядок дифференцирования не имеет значения, мы имеем  . Следовательно, . Следовательно, 
Если жесткость пластины при изгибе определяется как 
имеем 
При малых деформациях мы часто пренебрегаем пространственными производными от поперечного ускорения пластины, и остается 
Тогда в прямых тензорных обозначениях определяющее уравнение пластины имеет вид 
|
Ссылки
- ^А. Е. Х. Любовь, О малых свободных колебаниях и деформациях упругих оболочек, Философский пер. Королевского общества (Лондон), 1888 г., Vol. серия A, № 17 стр. 491–549.
- ^Редди, Дж. Н., 2007, Теория и анализ упругих пластин и оболочек, CRC Press, Тейлор и Фрэнсис.
- ^ Тимошенко, С., Войновски-Кригер, С., (1959), Теория пластин и оболочек, McGraw-Hill, New York.
См. Также
 Деформация тонкой пластины с выделением смещения, средней поверхности (красный цвет) и нормали к средней поверхности (синий)
Деформация тонкой пластины с выделением смещения, средней поверхности (красный цвет) и нормали к средней поверхности (синий) 















 Смещение средней поверхности (слева) и нормальной (справа)
Смещение средней поверхности (слева) и нормальной (справа) 






 Изгибающие моменты и нормальные напряжения
Изгибающие моменты и нормальные напряжения Моменты и касательные напряжения
Моменты и касательные напряжения
















![{\ begin {align} N _ {{\ alpha \ beta, \ alpha}} = 0 \\ M _ {{ \ alpha \ beta, \ alpha \ beta}} + [N _ {{\ alpha \ beta}} ~ w _ {{, \ beta}} ^ {0}] _ {{, \ alpha}} - q = 0 \ end {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/805c3eb5885064aa33be7d31e0e054995853f47a)





![D = 2h ^ {3} E / [3 (1- \ nu ^ {2})] = H ^ {3} E / [12 (1- \ nu ^ {2})]](https://wikimedia.org/api/rest_v1/media/math/render/svg/76681f1dbad8aed514809b36dd0dc21d8cd099f3)












![\ frac {1} {r} \ cfrac {d} {dr} \ left [r \ cfrac {d} {dr} \ left \ {\ frac { 1} {r} \ cfrac {d} {dr} \ left (r \ cfrac {dw} {dr} \ right) \ right \} \ right] = - \ frac {q} {D} \,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8083e6e16a9118c0afe8bd3c7e1fe841e17334)















