Кинетический Монте-Карло

редактировать

Метод кинетического Монте-Карло (KMC) - это компьютер метода Монте-Карло симуляция, предназначенная для моделирования временной эволюции некоторых процессов, происходящих в природе. Обычно это процессы, которые происходят с известной скоростью перехода между состояниями. Важно понимать, что эти ставки являются входными данными для алгоритма KMC, сам метод не может их предсказать.

Метод KMC по существу такой же, как динамический метод Монте-Карло и алгоритм Гиллеспи.

Содержание

1 Алгоритмы
- 1.1 KMC без отклонений
- 1.2 Отклонение KMC
2 Зависящие от времени алгоритмы
3 Комментарии к алгоритму
4 Примеры использования
5 История
6 Вариантов KMC
7 Ссылки
8 Внешние links

Алгоритмы

Одна из возможных классификаций алгоритмов KMC - KMC с отклонением (rKMC) и KMC без отклонения (rfKMC).

KMC без отклонений

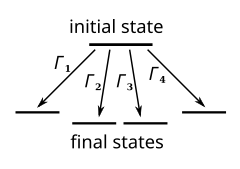На каждом шаге система может переходить в несколько конечных состояний, при этом предполагается, что скорости передачи между начальным состоянием и всеми возможными конечными состояниями известны.

Выбор из конечное состояние: случайная переменная выбирается между 0 и Γ tot ; вероятность того, что система перейдет в состояние i, пропорциональна Γ i.

. Алгоритм rfKMC, часто называемый KMC, для моделирования временной эволюции системы, где некоторые процессы могут происходить с известной скоростью r, может быть записан, например, как следующим образом:

Установить время $t = 0 {\ displaystyle t = 0}$ $t = 0$ .
Выбрать начальное состояние k.
Сформировать список всех $N k {\ displaystyle N_ {k}}$ $N_ {k}$ возможные скорости перехода в системе $rki {\ displaystyle r_ {ki}}$ $r_ {ki}$ из состояния k в общее состояние i. Состояния, которые не взаимодействуют с k, будут иметь $rki = 0 {\ displaystyle r_ {ki} = 0}$ $r_{ki}=0$ .
Расчет кумулятивной функции $R ki = ∑ j = 1 irkj {\ displaystyle R_ {ki} = \ sum _ {j = 1} ^ {i} r_ {kj}}$ $R_ {ki} = \ sum _ {j = 1} ^ {i} r_ {kj}$ для $i = 1,…, N k {\ displaystyle i = 1, \ ldots, N_ {k} }$ $i = 1, \ ldots, N_ {k }$ . Суммарный коэффициент: $Q k = R k, N k {\ displaystyle Q_ {k} = R_ {k, N_ {k}}}$ $Q_ {k} = R_ {k, N_ {k}}$ .
Получить равномерное случайное число $u ∈ (0, 1 ] {\ displaystyle u \ in (0,1]}$ $u \ in (0, 1]$ .
Найдите событие для выполнения i, найдя i, для которого $R k, i - 1 < u Q k ≤ R k i {\displaystyle R_{k,i-1}$ $R_ {k, i-1} <uQ_ { k} \ leq R_ {ki}$ (это может быть эффективно достигнуто с помощью двоичного поиска ).
Выполнить событие i (обновить текущее состояние $k → i {\ displaystyle k \ rightarrow i}$ $k \ rightarrow i$ ).
Получить новое равномерное случайное число $u ′ ∈ (0, 1] {\ displaystyle u ^ {\ prime} \ in (0,1]}$ $u ^ {\ prime} \ in (0,1]$ .
Обновите время с помощью $t = t + Δ t {\ displaystyle t = t + \ Delta t}$ $t = t + \ Delta t$ , где $Δ t = Q k - 1 ln ⁡ (1 / u ') {\ displaystyle \ Delta t = Q_ {k} ^ {- 1} \ ln (1 / u ^ {\ prime})}$ $\ Delta t = Q_ {k} ^ {- 1} \ ln (1 / u ^ {\ prime})$ .
Вернуться к шагу 3.

(Примечание: поскольку среднее значение $ln ⁡ (1 / u ′) {\ displaystyle \ ln (1 / u ^ {\ prime})}$ $\ ln (1 / u ^ {\ prime})$ равно единице, тот же средний масштаб времени можно получить, вместо этого используя $Δ t = Q k - 1 {\ displaystyle \ Delta t = Q_ {k} ^ {- 1}}$ $\ Delta t = Q_ {k} ^ {- 1}$ на шаге 9. Однако в этом случае задержка, связанная с переходом i не будет выводиться из распределения Пуассона, описываемого коэффициентом $Q k {\ displaystyle Q_ {k}}$ $Q_ {k}$ , а вместо этого будет средним значением этого распределения.)

Этот алгоритм известен в разных источниках под разными названиями: алгоритм времени пребывания, или n-кратный способ, или алгоритм Борца-Калоса-Лебовица (BKL). алгоритм. Важно отметить, что задействованный временной шаг является функцией вероятности того, что все события i не произошли.

KMC отклонения

KMC отклонения обычно имеет преимущество более простой обработки данных и более быстрых вычислений для каждого предпринятого шага, поскольку получение всех $rki {\ displaystyle r_ требует много времени. {ki}}$ $r_ {ki}$ не требуется. С другой стороны, время эволюции на каждом шаге меньше, чем для rfKMC. Относительный вес плюсов и минусов зависит от конкретного случая и доступных ресурсов.

rKMC, связанный с теми же скоростями перехода, что и выше, можно записать следующим образом:

Установить время $t = 0 {\ displaystyle t = 0}$ $t = 0$ .
Выбрать начальное состояние k.
Получить число $N k {\ displaystyle N_ {k}}$ $N_ {k}$ всех возможных скоростей перехода из состояния k в общее состояние i.
Найти событие-кандидат для выполнения i путем равномерной выборки из переходов $N k {\ displaystyle N_ {k}}$ $N_ {k}$ выше.
Принять событие с вероятностью $fki = rki / r 0 {\ displaystyle f_ {ki} = r_ {ki} / r_ {0}}$ $f_ {ki} = r_ {ki} / r_ {0}$ , где $r 0 {\ displaystyle r_ {0}}$ $r_ {0}$ - подходящая верхняя граница для $rki {\ displaystyle r_ {ki}}$ $r_ {ki}$ . Часто бывает легко найти $r 0 {\ displaystyle r_ {0}}$ $r_ {0}$ , не вычисляя все $rki {\ displaystyle r_ {ki}}$ $r_ {ki}$ (например,, для вероятностей скорости перехода в мегаполисе).
Если принято, выполнить событие i (обновить текущее состояние $k → i {\ displaystyle k \ rightarrow i}$ $k \ rightarrow i$ ).
Получить новое равномерное случайное число $u ′ ∈ (0, 1] {\ displaystyle u ^ {\ prime} \ in (0,1]}$ $u ^ {\ prime} \ in (0,1]$ .
Обновить время с помощью $t = t + Δ t {\ displaystyle t = t + \ Дельта t}$ $t = t + \ Delta t$ , где $Δ t = (N kr 0) - 1 ln ⁡ (1 / u ') {\ displaystyle \ Delta t = (N_ {k} r_ {0}) ^ {-1} \ ln (1 / u ^ {\ prime})}$ $\ Delta t = (N_ {k} r_ {0}) ^ {- 1} \ ln (1 / u ^ {\ prime})$ .
Вернуться к шагу 3.

(Примечание: $r 0 {\ displaystyle r_ {0}}$ $r_ {0}$ может изменяться от одного шага MC к другому.) Этот алгоритм обычно называется стандартным алгоритмом .

Были предоставлены теоретические и численные сравнения между алгоритмами.

Зависящие от времени алгоритмы

Если ставки $rki (t) {\ displaystyle r_ {ki} (t)}$ $r_ {ki} (t)$ зависят от времени, шаг 9 в rfKMC должен быть изменен по:

∫ 0 Δ t Q k (t ′) dt ′ = ln ⁡ (1 / u ′) {\ displaystyle \ int _ {0} ^ {\ Delta t} Q_ {k} (t ') dt '= \ ln (1 / u ^ {\ prime})}

\int _{0}^{\Delta t}Q_{k}(t')dt'=\ln(1/u^{\prime })

Реакция (шаг 6) должна быть выбрана после этого с помощью

R k, i - 1 (Δ t) < u Q k ( Δ t) ≤ R k i ( Δ t) {\displaystyle R_{k,i-1}(\Delta t)

R_ {k, i -1} (\ Delta t) <uQ_ {k} (\ Delta t) \ leq R_ {ki} (\ Delta t)

Другой очень похожий Алгоритм называется методом первой реакции (FRM). Он состоит из выбора первой реакции, то есть выбора наименьшего времени $Δ ti {\ displaystyle \ Delta t_ {i}}$ $\ Delta t_ {i}$ и соответствующего номера реакции i из формулы

∫ 0 Δ tirki (t ') dt' = ln ⁡ (1 / ui) {\ displaystyle \ int _ {0} ^ {\ Delta t_ {i}} r_ {ki} (t ') dt' = \ ln (1 / u_ {i})}

\int _{0}^{\Delta t_{i}}r_{ki}(t')dt'=\ln(1/u_{i})

где $ui ∈ (0, 1] {\ displaystyle u_ {i} \ in (0,1]}$ $u_ {i} \ in (0,1]$ - N случайных чисел.

Комментарии к алгоритму

Ключевым свойством алгоритма KMC (и алгоритма FRM) является то, что если скорости правильные, если процессы, связанные с ними, имеют Тип процесса Пуассона, и если разные процессы независимы (т. Е. Не коррелированы), то алгоритм KMC дает правильную шкалу времени для эволюции моделируемой системы. Были некоторые споры о правильности шкалы времени для алгоритмов rKMC, но это также было строго показано, чтобы быть правильным.

Если, кроме того, переходы следуют подробный баланс, алгоритм KMC можно использовать для моделирования термодинамического равновесия. Однако KMC широко используется для моделирования неравновесных процессов, и в этом случае нет необходимости соблюдать подробный баланс.

Алгоритм rfKMC эффективен в том смысле, что каждая итерация гарантированно производит переход. Однако в представленной выше форме он требует операций $N {\ displaystyle N}$ $N$ для каждого перехода, что не слишком эффективно. Во многих случаях это можно значительно улучшить, объединяя однотипные переходы в интервалы и / или формируя древовидную структуру данных событий. Недавно был разработан и протестирован алгоритм масштабирования с постоянным временем этого типа.

Главный недостаток rfKMC состоит в том, что все возможные скорости $rki {\ displaystyle r_ {ki}}$ $r_ {ki}$ и реакции должны быть известны заранее. Сам метод ничего не может сделать для их предсказания. Скорости и реакции должны быть получены с помощью других методов, таких как диффузионные (или другие) эксперименты, молекулярная динамика или моделирование на основе теории функционала плотности.

Примеры использования

KMC использовался при моделировании следующих физических систем:

Поверхностная диффузия
Подвижность дислокаций
Рост поверхности
Вакансия диффузия в сплавах (это было первоначальное использование)
Укрупнение эволюции доменов
Подвижность и кластеризация дефектов в твердых телах, облученных ионами или нейтронами, включая, помимо прочего, накопление повреждений и модели аморфизации / рекристаллизации.
Вязкоупругость физически сшитых сетей

Чтобы дать представление о том, что «объекты» и «события» могут быть на практике, вот один конкретный простой пример, соответствующий примеру 2 выше.

Рассмотрим систему, в которой отдельные атомы осаждаются на поверхности по одному (типично для физического осаждения из паровой фазы ), но также могут мигрировать по поверхности с некоторой известной скоростью скачка $ш {\ Displaystyle ш}$ $w$ . В этом случае «объектами» алгоритма KMC являются просто отдельные атомы.

Если два атома подходят вплотную друг к другу, они становятся неподвижными. Затем поток поступающих атомов определяет скорость r deposit, и система может быть смоделирована с помощью KMC, учитывая все осажденные подвижные атомы, которые (еще) не встретили своего двойника и стали неподвижными. Таким образом, на каждом шаге KMC возможны следующие события:

Новый атом приходит со скоростью 'r deposit
Уже отложенный атом перескакивает на один шаг со скоростью w.

После того, как событие произошло был выбран и выполнен с помощью алгоритма KMC, затем необходимо проверить, стал ли новый или только что перешедший атом непосредственно смежным с каким-либо другим атомом. Если это произошло, атом (атомы), которые теперь находятся рядом, необходимо удалить из списка мобильных атомов и, соответственно, удалить их события перехода из списка возможных событий.

Естественно, применяя КМК к проблемам физики и химии, нужно сначала подумать, достаточно ли хорошо реальная система следует допущениям, лежащим в основе КМК. Реальные процессы не обязательно имеют четко определенные скорости, переходные процессы могут быть коррелированы, в случае прыжков атома или частицы скачки могут не происходить в случайных направлениях и так далее. При моделировании сильно различающихся временных масштабов необходимо также учитывать, могут ли новые процессы присутствовать в более длительных временных масштабах. Если любая из этих проблем верна, временная шкала и развитие системы, предсказанные KMC, могут быть искажены или даже полностью неверны.

История

Первая публикация, описывающая основные особенности метода KMC (а именно использование кумулятивной функции для выбора события и вычисления шкалы времени в форме 1 / R), была написана Янгом. и Элкока в 1966 году. Примерно в то же время был опубликован алгоритм времени пребывания.

Очевидно, независимо от работ Янга и Элкока, Борц, Калос и Лебовиц разработали алгоритм KMC для моделирования Модель Изинга, которую они назвали n-кратным путем. Основы их алгоритма такие же, как у Янга, но они предоставляют гораздо более подробную информацию о методе.

В следующем году Дэн Гиллеспи опубликовал то, что сейчас известно как алгоритм Гиллеспи для описания химических реакций. Алгоритм аналогичен, а схема временного продвижения по существу такая же, как в KMC.

На момент написания этого (июнь 2006 г.) не существует окончательного трактата по теории KMC, но Фихторн и Вайнберг подробно обсудили теорию для моделирования термодинамического равновесия KMC. Хорошее введение дано также Art Voter, [1] и A.P.J. Янсен, [2], а недавний обзор - (Chatterjee 2007) или (Chotia 2008).

В марте 2006 года, вероятно, первое коммерческое программное обеспечение, использующее кинетический Монте-Карло для моделирования диффузия и активация / дезактивация примесей в кремнии и кремнийподобных материалах выпущена Synopsys, сообщается Martin-Bragado et al.

Разновидности KMC

Метод KMC можно подразделить по тому, как движутся объекты или происходят реакции. Используются по меньшей мере следующие подразделения:

Решетка KMC (LKMC ) означает KMC, выполняемую на атомарной решетке. Часто эту разновидность также называют атомистической КМС (AKMC ). Типичным примером является моделирование вакансии диффузии в сплавах, где вакансия может прыгать по решетке со скоростью, зависящей от локальный элементный состав.
Объект KMC (OKMC ) означает KMC, проведенный для дефектов или примесей, которые скачут случайно или решетки-специфические направления. В моделирование включаются только положения прыгающих объектов, а не положения «фоновых» атомов решетки. Базовый шаг KMC - это переход на один объект.
Событие KMC (EKMC ) или KMC первого прохода (FPKMC ) означает разновидность OKMC, где следующая реакция между объектами (например, кластеризация двух примесей или вакансий - межузельная аннигиляция ) выбирается с помощью алгоритма KMC с учетом положения объектов, и это событие затем немедленно

Литература

Внешние ссылки