Формат с плавающей запятой половинной точности

редактировать

16-битный формат компьютерных чисел

В вычислениях, половинная точность (иногда называемая FP16 ) - это двоичный плавающая точка формат компьютерных чисел который занимает 16 бит (два байта в современных компьютерах) в памяти компьютера.

. Они могут выражать значения в диапазоне ± 65,504 с точностью до 0,0000000596046.

В стандарте IEEE 754-2008 16-битный формат base-2 упоминается как binary16 . Он предназначен для хранения значений с плавающей запятой в приложениях, где более высокая точность не важна для выполнения арифметических вычислений.

Хотя реализации IEEE с плавающей запятой половинной точности являются относительно новыми, существовало несколько более ранних 16-битных форматов с плавающей запятой, в том числе Hitachi HD61810 DSP 1982 года, WIF Скотта и графический процессор 3dfx Voodoo Graphics..

Nvidia и Microsoft определили halfтип данных в языке Cg, выпущенном в начале 2002 года, и реализовали его. в кремнии в GeForce FX, выпущенном в конце 2002 года. ILM искал формат изображения, который мог бы обрабатывать широкий динамический диапазон, но без жесткого диска и стоимость памяти для представлений с плавающей запятой, которые обычно используются для вычислений с плавающей запятой (одинарной и двойной точности). Группа программируемого затенения с аппаратным ускорением во главе с Джоном Эйри из SGI (Silicon Graphics) изобрела тип данных s10e5 в 1997 году в рамках проекта «bali». Это описано в статье SIGGRAPH 2000 (см. Раздел 4.3) и дополнительно задокументировано в патенте США 7518615.

Этот формат используется в нескольких средах компьютерной графики, включая MATLAB, OpenEXR, JPEG XR, GIMP, OpenGL, Cg, Direct3D и D3DX. Преимущество перед 8-битными или 16-битными двоичными целыми числами заключается в том, что увеличенный динамический диапазон позволяет сохранять больше деталей в светлых участках и тенях для изображений. Преимущество перед 32-битными двоичными форматами одинарной точности состоит в том, что для этого требуется половина объема памяти и пропускная способность (за счет точности и диапазона).

56>F16C расширение позволяет процессорам x86 преобразовывать числа с плавающей запятой половинной точности в и обратно числа с плавающей запятой одинарной точности.

В зависимости от компьютера половинная точность может быть на порядок быстрее, чем двойная точность, например 37 PFLOPS против для половины 550 "AI-PFLOPS (Half Precision)".

Содержание

1 IEEE 754 двоичный формат с плавающей запятой половинной точности: binary16
- 1.1 Экспонентное кодирование
- 1.2 Примеры половинной точности
- 1.3 Ограничения точности для десятичных значений в [0, 1]
- 1.4 Ограничения точности для десятичных значений в [1, 2048]
- 1.5 Ограничения точности для целочисленных значений
2 Альтернатива ARM с половинной точностью
3 Использует
4 См. Также
5 Ссылки
6 Дополнительная литература
7 Внешние ссылки

Двоичный формат с плавающей запятой половинной точности IEEE 754: binary16

IEEE 754 стандарт определяет binary16 как имеющий следующий формат:

бит знака : 1 бит
экспонента ширина: 5 бит
значащая точность : 11 бит (10 явно сохраненных)

Формат представлен следующим образом:

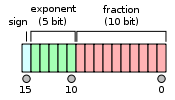
Предполагается, что формат имеет неявный ведущий бит со значением 1, если только поле экспоненты не сохранено со всеми нулями. Таким образом, в формате памяти появляется только 10 битов значения значимости, но общая точность составляет 11 бит. В языке IEEE 754 имеется 10 значащих битов, но есть 11 битов значимой точности (log 10 (2) ≈ 3,311 десятичных цифр, или 4 цифры ± немного меньше 5 единиц в последнее место ).

Кодирование экспоненты

Показатель степени с плавающей запятой половинной точности кодируется с использованием представления смещение-двоичное с нулевым смещением 15; также известный как смещение экспоненты в стандарте IEEE 754.

Eмин = 00001 2 - 01111 2 = −14
Eмакс = 11110 2 - 01111 2 = 15
Смещение экспоненты = 01111 2 = 15

Таким образом, как определено двоичным представлением смещения, для получения истинного показателя смещение 15 должно быть вычитается из хранимой экспоненты.

Сохраненные экспоненты 00000 2 и 11111 2 интерпретируются специально.

Показатель	Знаки = ноль	Знаки ≠ ноль	Уравнение
00000 2	ноль, −0	субнормальные числа	(-1) × 2 × 0. значащие биты 2
00001 2,..., 11110 2	нормализованное значение		(-1) × 2 × 1. значащие биты 2
11111 2	±бесконечность	NaN (тихий, сигнальный)

Минимальное строго положительное (субнормальное) значение составляет 2 ≈ 5,96 × 10. Минимальное положительное нормальное значение составляет 2 ≈ 6,10 × 10. Максимальное представимое значение - (2 -2) × 2 = 65504.

Примеры половинной точности

Эти примеры даны в битовом представлении значения с плавающей запятой. Это включает знаковый бит, (смещенную) экспоненту и мантиссу.

0 00000 0000000001 2 = 0001 16=  $2–14 × (0 + 1 1024) {\ displaystyle 2 ^ {- 14} \ times (0 + {\ frac {1 } {1024}})}$  ${\ displaystyle 2 ^ {- 14} \ times (0 + {\ frac {1} {1024}})}$ ≈ 0,000000059604645 (наименьшее положительное субнормальное число)

0 00000 1111111111 2 = 03ff 16=  $2 - 14 × (0 + 1023 1024) {\ displaystyle 2 ^ {- 14} \ times (0 + {\ frac {1023} {1024}})}$  ${\ displaystyle 2 ^ {- 14} \ times (0 + {\ frac {1023} {1024}})}$ ≈ 0,000060975552 (наибольшее субнормальное число)

0 00001 0000000000 2 = 0400 16=  $2–14 × (1 + 0 1024) {\ displaystyle 2 ^ {- 14} \ times (1 + {\ frac {0} {1024}})}$  ${\ displaystyle 2 ^ {- 14} \ times (1 + {\ frac {0} {1024}})}$ ≈ 0,000061035156 (наименьшее положительное нормальное число)

0 11110 1111111111 2 = 7bff 16=  $2 15 × (1 + 1023 1024) {\ displaystyle 2 ^ {15} \ times (1 + {\ frac {1023} {1024}})}$  ${\ displaystyle 2 ^ {15} \ times (1 + {\ frac {1023} {1024}})}$ = 65504 (наибольшее нормальное число)

0 01110 1111111111 2 = 3bff 16=  $2 - 1 × (1 + 1023 1024) {\ displaystyle 2 ^ {- 1} \ times (1 + {\ frac {1023} {1024}})}$  ${\ displaystyle 2 ^ {- 1} \ times (1 + {\ frac {1023} {1024}})}$ ≈ 0,99951172 (наибольшее число меньше один)

0 01111 0000000000 2 = 3c00 16=  $2 0 × (1 + 0 1024) {\ displaystyle 2 ^ {0} \ tim es (1 + {\ frac {0} {1024}})}$  ${\ displaystyle 2 ^ {0} \ times (1 + {\ frac {0} { 1024}})}$ = 1 (один)

0 01111 0000000001 2 = 3c01 16=  $2 0 × (1 + 1 1024) {\ displaystyle 2 ^ {0} \ times (1 + {\ frac {1} {1024}})}$  ${\ displaystyle 2 ^ {0} \ times (1 + {\ frac {1} {1024}})}$ ≈ 1.00097656 (наименьшее число больше единицы)

0 01101 0101010101 2 = 3555 16=  $2–2 × (1 + 341 1024) {\ displaystyle 2 ^ {- 2} \ times (1 + {\ frac {341} {1024 }})}$  ${\ displaystyle 2 ^ {- 2} \ times (1 + {\ frac {341} {1024}}) }$ = 0,33325195 (округление от 1/3 до ближайшего)

1 10000 0000000000 2 = c000 16 = −2

0 00000 0000000000 2 = 0000 16 = 0 1 00000 0000000000 2 = 8000 16 = −0

0 11111 0000000000 2 = 7c00 16 = бесконечность 1 11111 0000000000 2 = fc00 16 = −infinity

По умолчанию 1/3 округляется в меньшую сторону, как для двойной точности, из-за нечетного числа бит в мантиссе. Таким образом, биты за точкой округления равны 0101..., что меньше 1/2 единицы на последнем месте.

Ограничения точности для десятичных значений в [0, 1]

Десятичные числа между 2 (минимальное положительное отклонение от нормы) и 2 (максимальное отклонение от нормы): фиксированный интервал 2
Десятичное число между 2 (минимальное положительное отклонение нормы) и 2: фиксированный интервал 2
Десятичное число от 2 до 2: фиксированный интервал 2
Десятичные числа от 2 до 2: фиксированный интервал 2
Десятичные числа между 2 и 2: фиксированный интервал 2
Десятичные числа между 2 и 2: фиксированный интервал 2
Десятичные числа между 2 и 2: фиксированный интервал 2
Десятичные знаки между 2 и 2: фиксированный интервал 2
Десятичные знаки между 2 и 2: фиксированный интервал 2
Десятичные числа между 2 и 2: фиксированный интервал 2
Десятичные знаки между 2 и 2: фиксированный интервал 2
Десятичные знаки между 2 и 2: фиксированный интервал 2
Десятичные знаки между 2 и 2: фиксированный интервал 2
Десятичные числа от 2 до 2: фиксированный интервал 2
Десятичные числа от 2 до 2: фиксированный интервал 2

Ограничения точности для десятичных значений в [1, 2048]

Десятичные числа от 1 до 2: фиксированный интервал 2 (1 + 2 - следующее по величине число с плавающей запятой после 1)
Десятичные числа между 2 и 4: фиксированный интервал 2
Десятичные числа от 4 до 8: фиксированный интервал 2
Десятичные числа от 8 до 16: фиксированный интервал 2
Десятичные числа от 16 до 32: фиксированный интервал 2
Десятичные числа от 32 до 64: фиксированный интервал 2
Десятичные числа от 64 до 128: фиксированный интервал 2
Десятичные числа от 128 до 256: фиксированный интервал 2
Десятичные числа от 256 до 512: фиксированный интервал 2
Десятичные знаки между 512 и 1024: фиксированный интервал 2
Десятичные числа между 1024 и 2048: фиксированный интервал 2

Ограничения точности для целочисленных значений

Целые числа от 0 до 2048 могут быть точно представлены (а также между -2048 и 0)
Целые числа от 2048 до 4096 округляются до кратного 2 (четное число)
Целые числа от 4096 и 8192 округлить до кратного 4
Int Например, число от 8192 до 16384 округляется до кратного 8
Целого числа от 16384 до 32768 округляется до кратного 16
Целого числа от 32768 до 65519 округляется до кратного 32
Целые числа выше 65519 округляются до "бесконечности" при использовании округления до четности, выше 65535 при использовании округления до нуля или выше 65504 при использовании округления до бесконечности.

Альтернативный вариант ARM с половинной точностью

Процессоры ARM поддерживают (через регистр управления с плавающей запятой бит) формат «альтернативной половинной точности», который устраняет особый случай для значения экспоненты 31 (11111 2). Он почти идентичен формату IEEE, но в нем нет кодирования для бесконечности или NaN; вместо этого показатель степени 31 кодирует нормализованные числа в диапазоне от 65536 до 131008.

Использует

Аппаратное и программное обеспечение для машинного обучения или нейронных сетей как правило, используют половинную точность: такие приложения обычно выполняют большой объем вычислений, но не требуют высокого уровня точности.

На старых компьютерах, которые обращаются к 8 или 16 битам за раз (большинство современных компьютеров обращаются к 32 или 64 битам за раз), арифметика половинной точности выполняется быстрее, чем одинарная точность, и значительно быстрее, чем двойная точность. В системах с инструкциями, которые могут обрабатывать несколько чисел с плавающей запятой с помощью одной инструкции, половинная точность часто обеспечивает более высокую среднюю пропускную способность.

См. Также

Формат с плавающей запятой bfloat16 : альтернативный 16-битный формат с плавающей запятой с 8 битами экспоненты и 7 битами мантиссы
IEEE 754 : стандарт IEEE для арифметики с плавающей запятой (IEEE 754)
ISO / IEC 10967, независимая от языка арифметика
Примитивный тип данных
Формат изображения RGBE

Ссылки

Дополнительная литература

Подписанный Хронос Вулкан 16-битный формат с плавающей запятой

Внешние ссылки

Minifloats (в Обзоре Форматы с плавающей запятой)
Сайт OpenEXR
Константы половинной точности из D3DX
Обработка OpenGL половинной точности
Быстрые преобразования половинной точности
Вариант аналоговых устройств (четыре -битная экспонента)
Исходный код C для преобразования между двойной, одинарной и половинной точностью IEEE можно найти здесь
Исходный код Java для преобразования половинной точности с плавающей запятой
Плавающая точка половинной точности для одной из расширенных функций GCC