Групповое тестирование

Процедура, которая разбивает задачу идентификации определенных объектов на тесты по группам элементов.

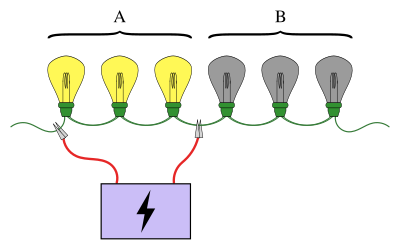
Иллюстрация проблемы с лампочкой, где среди шести лампочек ищут сломанную лампочку. Здесь первые три подключены к источнику питания, и они загораются (A). Это означает, что сломанная лампа должна быть одной из трех последних (B). Если бы вместо этого лампочки не загорелись, можно было быть уверенным, что сломанная лампочка была среди первых трех. Продолжая эту процедуру, можно найти сломанную лампу не более чем в трех тестах, по сравнению с максимум шестью тестами, если лампы проверяются индивидуально.

В статистике и комбинаторной математике, групповое тестирование - это любая процедура, которая разбивает задачу идентификации определенных объектов на тесты по группам элементов, а не по отдельным. Групповое тестирование, впервые изученное Робертом Дорфманом в 1943 году, представляет собой относительно новую область прикладной математики, которая может применяться к широкому кругу практических приложений и является активной областью исследований сегодня.

Знакомый пример группового тестирования включает последовательность лампочек, соединенных последовательно, причем известно, что одна из ламп сломана. Цель состоит в том, чтобы найти сломанную лампочку с помощью наименьшего количества тестов (где тест - это когда некоторые из лампочек подключены к источнику питания). Простой подход - проверить каждую лампочку индивидуально. Однако при большом количестве луковиц гораздо эффективнее объединять луковицы в группы. Например, подключив первую половину ламп сразу, можно определить, в какой половине разбитая лампочка, исключив половину ламп всего за один тест.

Схемы для проведения группового тестирования могут быть простыми или сложными, и тесты, задействованные на каждом этапе, могут быть разными. Схемы, в которых тесты для следующего этапа зависят от результатов предыдущих этапов, называются адаптивными процедурами, а схемы, разработанные так, чтобы все тесты были известны заранее, называются неадаптивными процедурами. Структура схемы тестов, задействованных в неадаптивной процедуре, известна как план объединения.

Групповое тестирование имеет множество приложений, включая статистику, биологию, информатику, медицину, инженерию и кибербезопасность. Современный интерес к этим схемам тестирования возродился благодаря проекту Human Genome Project.

• 1 Базовое описание и термины
  • 1.1 Классификация задач группового тестирования
  • 1.2 Варианты и расширения
• 2 История и развитие
  • 2.1 Изобретение и начальный прогресс
  • 2.2 Комбинаторное групповое тестирование
  • 2.3 Неадаптивное и вероятностное тестирование
• 3 Формализация комбинаторного группового тестирования
  • 3.1 Общие границы
    • 3.1.1 Информация нижняя граница
  • 3.2 Представление неадаптивных алгоритмов
  • 3.3 Границы для неадаптивных алгоритмов
• 4 Обобщенный алгоритм двоичного расщепления
• 5 Неадаптивные алгоритмы
  • 5.1 Комбинаторное поисковое ортогональное сопоставление (COMP)
  • 5.2 Определенные дефекты (DD)
  • 5.3 Последовательный COMP (SCOMP)
• 6 Примеры приложений
  • 6.1 Каналы множественного доступа
  • 6.2 Машинное обучение и сжатое зондирование
  • 6.3 Дизайн мультиплексного анализа для тестирования COVID19
  • 6.4 Криминалистика данных
• 7 Примечания
• 8 Ссылки
  • 8.1 Цитаты
  • 8.2 Общие ссылки
• 9 См. Также

В отличие от многих областей математики происхождение группового тестирования можно проследить до одного отчета, написанного одним человеком: Роберт Дорфман. Мотивация возникла во время Второй мировой войны, когда Служба общественного здравоохранения США и Служба выборочного контроля приступили к крупномасштабному проекту по отсеиванию всех сифилитических мужчин. вызвали на индукцию. Тестирование человека на сифилис включает взятие у него образца крови, а затем анализ этого образца для определения наличия или отсутствия сифилиса. В то время выполнение этого теста было дорогостоящим, а тестирование каждого солдата по отдельности было бы очень дорогим и неэффективным.

Предположим, что есть $n\; \{\backslash \; displaystyle\; n\}$солдат, это метод тестирования приводит к $n\; \{\backslash \; displaystyle\; n\}$отдельным тестам. Если большая часть людей инфицирована, этот метод будет разумным. Однако в более вероятном случае, когда инфицирована лишь очень небольшая часть мужчин, может быть реализована гораздо более эффективная схема тестирования. Возможность создания более эффективной схемы тестирования зависит от следующего свойства: солдат можно объединять в группы, и в каждой группе образцы крови можно объединять. Затем объединенный образец можно проверить, чтобы проверить, есть ли по крайней мере один солдат в группе сифилисом. Это центральная идея группового тестирования. Если один или несколько солдат в этой группе болеют сифилисом, то тест считается бесполезным (необходимо провести дополнительные тесты, чтобы определить, какой это солдат (-а)). С другой стороны, если ни у кого в пуле нет сифилиса, то многие тесты сохраняются, так как каждый солдат в этой группе может быть уничтожен только одним тестом.

Пункты, которые вызывают положительный результат теста в группе, обычно являются называются бракованными предметами (это сломанные лампочки, сифилитики и т. д.). Часто общее количество элементов обозначается как $n\; \{\backslash \; displaystyle\; n\}$, а $d\; \{\backslash \; displaystyle\; d\}$представляет количество дефектов, если это предполагается. быть известным.

Классификация задач группового тестирования

Есть две независимые классификации проблем группового тестирования; каждая проблема группового тестирования является либо адаптивной, либо неадаптивной, либо вероятностной, либо комбинаторной.

В вероятностных моделях предполагается, что дефектные элементы подчиняются некоторому распределению вероятностей, и цель состоит в том, чтобы свести к минимуму ожидаемое количество тестов, необходимых для выявления дефектности каждого элемента. С другой стороны, при комбинаторном групповом тестировании цель состоит в том, чтобы минимизировать количество тестов, необходимых в «наихудшем сценарии», то есть создать алгоритм minmax, и не знать распределения предполагается наличие дефектов.

Другая классификация, адаптивность, касается того, какую информацию можно использовать при выборе элементов для группировки в тест. Как правило, выбор элементов для тестирования может зависеть от результатов предыдущих тестов, как в случае с лампочкой выше. Алгоритм , который продолжает выполнение теста, а затем использует результат (и все прошлые результаты), чтобы решить, какой следующий тест выполнить, называется адаптивным. И наоборот, в неадаптивных алгоритмах все тесты решаются заранее. Эту идею можно обобщить на многоступенчатые алгоритмы, где тесты разделены на этапы, и каждый тест на следующем этапе должен быть решен заранее, только с учетом результатов тестов на предыдущих этапах. Хотя адаптивные алгоритмы предлагают гораздо больше свободы в разработке, известно, что алгоритмы адаптивного группового тестирования не улучшают неадаптивные алгоритмы более чем на постоянный коэффициент в количестве тестов, необходимых для выявления набора дефектных элементов. В дополнение к этому неадаптивные методы часто полезны на практике, потому что можно продолжить последовательные тесты без предварительного анализа результатов всех предыдущих тестов, что позволяет эффективно распределить процесс тестирования.

Варианты и расширения

Есть много способов расширить проблему группового тестирования. Одно из наиболее важных - это групповое тестирование с шумом, и оно связано с большим предположением об исходной проблеме: это тестирование безошибочно. Проблема группового тестирования называется зашумленной, если есть некоторая вероятность того, что результат группового теста будет ошибочным (например, будет положительным, если тест не содержит дефектов). Модель шума Бернулли предполагает, что эта вероятность является некоторой константой, $q\; \{\backslash \; displaystyle\; q\}$, но в целом она может зависеть от истинного количества дефектов в тесте и количества тестируемых элементов. Например, эффект разбавления можно смоделировать, сказав, что положительный результат более вероятен, когда в тесте присутствует больше дефектов (или больше дефектов в виде доли от числа протестированных). Шумный алгоритм всегда будет иметь ненулевую вероятность ошибки (то есть неправильной маркировки элемента).

Групповое тестирование можно расширить, рассматривая сценарии, в которых существует более двух возможных результатов теста. Например, тест может иметь результаты $0,\; 1\; \{\backslash \; displaystyle\; 0,1\}$и $2\; +\; \{\backslash \; displaystyle\; 2\; ^\; \{+\}\}$, соответствует отсутствию дефектов, единственному дефекту или неизвестному количеству дефектов больше единицы. В более общем плане можно считать, что набор результатов теста равен $0,\; 1,\dots ,\; k\; +\; \{\backslash \; displaystyle\; \{0,1,\; \backslash \; ldots,\; k\; ^\; \{+\}\}\}$для некоторого $k\; \in \; N\; \{\backslash \; displaystyle\; k\; \backslash \; in\; \backslash \; mathbb\; \{N\}\}$.

Другое расширение - рассмотрение геометрических ограничений на то, какие наборы могут быть проверены. Вышеупомянутая проблема с лампочкой является примером такого ограничения: только лампочки, которые появляются последовательно, могут быть проверены. Аналогичным образом элементы могут быть расположены по кругу или, в общем, в виде сети, где тесты представляют собой доступные пути на графе. Другой вид геометрического ограничения - это максимальное количество элементов, которые могут быть протестированы в группе, или размеры групп могут быть одинаковыми и так далее. Подобным образом может быть полезно рассмотреть ограничение, согласно которому любой заданный элемент может появляться только в определенном количестве тестов.

Есть бесконечные способы продолжить переделывать базовую формулу группового тестирования. Следующие уточнения дадут представление о некоторых из наиболее экзотических вариантов. В модели «хорошо – посредственно – плохо» каждый элемент является одним из «хорошо», «посредственно» или «плохо», а результат теста является типом «худшего» элемента в группе. При пороговом групповом тестировании результат теста положительный, если количество дефектных элементов в группе превышает некоторое пороговое значение или пропорцию. Групповое тестирование с ингибиторами - это вариант с приложениями в молекулярной биологии. Здесь есть третий класс элементов, называемых ингибиторами, и результат теста положительный, если он содержит хотя бы один дефект и не содержит ингибиторов.

Изобретение и начальный прогресс

Концепция группового тестирования была впервые представлена ​​Робертом Дорфманом в 1943 году в коротком отчете, опубликованном в разделе «Примечания» журнала Annals of Mathematical Statistics. Отчет Дорфмана - как и все ранние работы по групповому тестированию - был сосредоточен на вероятностной проблеме и был направлен на использование новой идеи группового тестирования, чтобы сократить ожидаемое количество тестов, необходимых для отсеивания всех сифилитических мужчин в данном пуле солдат. Метод был прост: разделите солдат на группы заданного размера и используйте индивидуальное тестирование (тестирование предметов в группах первого размера) на положительных группах, чтобы определить, какие из них были инфицированы. Дорфман свел в таблицу оптимальные размеры групп для этой стратегии с учетом уровня распространенности дефективности в популяции.

После 1943 года групповое тестирование оставалось в основном неизменным в течение ряда лет. Затем в 1957 году Стерретт улучшил процедуру Дорфмана. Этот новый процесс начинается с повторного индивидуального тестирования положительных групп, но останавливается, как только обнаруживается дефект. Затем остальные элементы в группе проверяются вместе, поскольку очень вероятно, что ни один из них не является дефектным.

Первое тщательное рассмотрение группового тестирования было дано Собелом и Гроллом в их формирующей статье 1959 года по этому вопросу. Они описали пять новых процедур - в дополнение к обобщениям для случаев, когда уровень распространенности неизвестен - и для наиболее оптимальной из них они предоставили явную формулу для ожидаемого количества тестов, которые она будет использовать. В статье также впервые была установлена ​​связь между групповым тестированием и теорией информации, а также обсуждены некоторые обобщения проблемы группового тестирования и представлены некоторые новые приложения теории.

Комбинаторное групповое тестирование

Групповое тестирование было впервые изучено в комбинаторном контексте Ли в 1962 году с введением Ли $s\; \{\backslash \; displaystyle\; s\}$- этапный алгоритм. Ли предложил расширить «двухэтапный алгоритм» Дорфмана на произвольное количество этапов, для которых требуется не более $t\; =\; e\; log\; 2\; \; (e)\; d\; log\; 2\; \; (n)\; \{\backslash \; displaystyle\; t\; =\; \{\backslash \; frac\; \{e\}\; \{\backslash \; log\; \_\; \{2\}\; (e)\}\}\; d\; \backslash \; log\; \_\; \{2\}\; (n)\}$тесты, чтобы гарантированно найти $d\; \{\backslash \; displaystyle\; d\}$или меньше дефектов среди $n\; \{\backslash \; displaystyle\; n\}$элементов. Идея заключалась в том, чтобы удалить все элементы из отрицательных тестов и разделить оставшиеся элементы на группы, как это было сделано с исходным пулом. Это должно было быть выполнено $с\; -\; 1\; \{\backslash \; displaystyle\; s-1\}$раз перед выполнением индивидуального тестирования.

Комбинаторное групповое тестирование в целом было позже более полно изучено Катоной в 1973 году. Катона представила матричное представление неадаптивного группового тестирования и разработала процедуру для поиска дефектов в неадаптивных -адаптивный 1-дефектный случай не более чем $t\; =\; \lceil \; log\; 2\; \; (n)\; \rceil \; \{\backslash \; displaystyle\; t\; =\; \backslash \; lceil\; \backslash \; log\; \_\; \{2\}\; (n)\; \backslash \; rceil\}$тестов, что он также оказался оптимальным.

В общем, найти оптимальные алгоритмы для адаптивного комбинаторного группового тестирования сложно, и хотя вычислительная сложность группового тестирования не была определена, предполагается, что это сложно в каком-то классе сложности. Однако в 1972 году произошел важный прорыв с введением обобщенного алгоритма двоичного расщепления. Обобщенный алгоритм двоичного разделения работает, выполняя двоичный поиск в группах с положительным результатом теста, и представляет собой простой алгоритм, который находит один дефект не более чем в нижней границе информации количество тестов.

В сценариях, где есть два или более дефекта, обобщенный алгоритм двоичного разделения по-прежнему дает почти оптимальные результаты, требуя не более $d\; -\; 1\; \{\backslash \; displaystyle\; d-1\}$проверяет над нижней границей информации, где $d\; \{\backslash \; displaystyle\; d\}$- количество дефектов. Существенные улучшения были внесены в 2013 г. Аллеманом: требуемое количество тестов составило менее $0,187\; d\; +\; 0,5\; log\; 2\; \; (d)\; +\; 5,5\; \{\backslash \; displaystyle\; 0,187d\; +\; 0,5\; \backslash \; log\; \_\; \{2\}\; (d)\; +5,5\}$над нижней границей информации, когда $n\; /\; d\; \ge \; 38\; \{\backslash \; displaystyle\; n\; /\; d\; \backslash \; geq\; 38\}$и $d\; \ge \; 10\; \{\backslash \; displaystyle\; d\; \backslash \; geq\; 10\}$. Это было достигнуто путем изменения двоичного поиска в алгоритме двоичного разбиения на сложный набор подалгоритмов с перекрывающимися тестовыми группами. Таким образом, проблема адаптивного комбинаторного группового тестирования - с известным числом или верхней границей количества дефектов - по существу решена, и есть мало возможностей для дальнейшего улучшения.

Остается открытым вопрос, когда индивидуальное тестирование составляет minmax. Ху, Хван и Ван показали в 1981 году, что индивидуальное тестирование минимально, когда $n\; \le \; \lfloor \; (5\; d\; +\; 1)\; /\; 2\; \rfloor \; \{\backslash \; displaystyle\; n\; \backslash \; leq\; \backslash \; lfloor\; (5d\; +\; 1)\; /\; 2\; \backslash \; rfloor\}$, и что это не minmax, когда $n>3\; d\; \{\backslash \; displaystyle\; n>3d\}$. В настоящее время предполагается, что эта граница является точной: то есть индивидуальное тестирование минимально, если и только если $n\; \le \; 3\; d\; \{\backslash \; displaystyle\; n\; \backslash \; leq\; 3d\}$. Некоторый прогресс был достигнут в 2000 году Риччио и Колборном, которые показали, что для больших $n\; \{\backslash \; displaystyle\; n\}$, индивидуальное тестирование минимально, когда $d\; \ge \; n\; /\; log\; 3/2\; \; (3)\; \approx \; 0,369\; n\; \{\backslash \; displaystyle\; d\; \backslash \; geq\; n\; /\; \backslash \; log\; \_\; \{3/2\}\; (3)\; \backslash \; приблизительно\; 0,369n\}$.

Неадаптивное и вероятностное тестирование

Одним из ключевых выводов неадаптивного группового тестирования является то, что значительный выигрыш может быть получен путем устранения требования о том, что процедура группового тестирования b Он наверняка увенчается успехом («комбинаторная» проблема), но скорее позволит ему иметь некоторую низкую, но ненулевую вероятность неправильной маркировки каждого элемента («вероятностная» проблема). Известно, что по мере того, как количество дефектных элементов приближается к общему количеству элементов, точные комбинаторные решения требуют значительно большего количества тестов, чем вероятностные решения - даже вероятностные решения допускают только асимптотически малую вероятность ошибки.

В этом ключе Chan et al. (2011) представили COMP, вероятностный алгоритм, который требует не более $t\; =\; ed\; (1\; +\; \delta )\; ln\; \; (n)\; \{\backslash \; displaystyle\; t\; =\; ed\; (1+\; \backslash \; delta)\; \backslash \; ln\; (n)\}$тесты, чтобы найти до $d\; \{\backslash \; displaystyle\; d\}$дефектов в $n\; \{\backslash \; displaystyle\; n\}$элементах с вероятность ошибки не более $n\; -\; \delta \; \{\backslash \; displaystyle\; n\; ^\; \{-\; \backslash \; delta\}\}$. Это находится в пределах постоянного множителя $t\; =\; O\; (d\; log\; 2\; \; n)\; \{\backslash \; displaystyle\; t\; =\; O\; (d\; \backslash \; log\; \_\; \{2\}\; n)\}$нижней границы.

Чан и др. (2011) также представили обобщение COMP до простой шумной модели и аналогичным образом получили явную границу производительности, которая снова была только константой (зависящей от вероятности неудачного теста) выше соответствующей нижней границы. В общем, количество тестов, требуемых в случае шума Бернулли, на постоянный коэффициент больше, чем в случае отсутствия шума.

Олдридж, Балдассини и Джонсон (2014) разработали расширение алгоритма COMP, которое добавило дополнительные пост- этапы обработки. Они показали, что производительность этого нового алгоритма, названного DD, строго превосходит производительность COMP, и что DD является «по существу оптимальным» в сценариях, где $d\; 2\; \ge \; n\; \{\backslash \; displaystyle\; d\; ^\; \{2\; \}\; \backslash \; geq\; n\}$, сравнивая его с гипотетическим алгоритмом, определяющим разумный оптимум. Производительность этого гипотетического алгоритма предполагает, что есть возможности для улучшения, когда , а также предполагает, насколько это может быть улучшением.

В этом разделе формально определены понятия и термины, относящиеся к групповому тестированию.

• Входной вектор, $x\; =\; (x\; 1,\; x\; 2,\dots ,\; xn)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\; =\; (x\_\; \{1\},\; x\_\; \{2\},\; \backslash \; dots,\; x\_\; \{n\}))\}$, определяется как двоичный вектор длины $n\; \{\backslash \; displaystyle\; n\}$(то есть $x\; \in \; \{0,\; 1\}\; n\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\; \backslash \; in\; \backslash \; \{0,1\; \backslash \}\; ^\; \{n\}\}$), причем j-й элемент называется дефектным тогда и только тогда, когда $xj\; =\; 1\; \{\backslash \; displaystyle\; x\_\; \{j\}\; =\; 1\}$. Кроме того, любой исправный элемент называется «хорошим».

$x\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\}$предназначен для описания (неизвестного) набора дефектных элементов. Ключевым свойством $x\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\}$является то, что это неявный ввод. Другими словами, нет прямого знания о том, что представляют собой записи $x\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\}$, кроме тех, которые могут быть выведены с помощью некоторой серии «тестов». Это приводит к следующему определению.

• Пусть $x\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\}$будет входным вектором. Набор, $S\; \subseteq \; \{1,\; 2,\dots ,\; n\}\; \{\backslash \; displaystyle\; S\; \backslash \; substeq\; \backslash \; \{1,2,\; \backslash \; dots,\; n\; \backslash \}\}$называется тестом. При бесшумном тестировании результат теста положительный, если существует $j\; \in \; S\; \{\backslash \; displaystyle\; j\; \backslash \; in\; S\}$такое, что $xj\; =\; 1\; \{\backslash \; displaystyle\; x\_\; \{j\}\; =\; 1\}$, в противном случае результат будет отрицательным.

Таким образом, цель группового тестирования состоит в том, чтобы найти метод выбора «короткой» серии тестов, допускающих $x\; \{\; \backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\}$подлежит определению точно или с высокой степенью уверенности.

• Считается, что алгоритм группового тестирования делает ошибку, если он неправильно маркирует элемент (то есть маркирует любой дефектный элемент как недефектный или наоборот). Это не то же самое, что результат неправильного группового теста. Алгоритм называется нулевой ошибкой, если вероятность того, что он делает ошибку, равна нулю.
• $t\; (d,\; n)\; \{\backslash \; displaystyle\; t\; (d,\; n)\}$обозначает минимальное количество необходимых тестов. всегда находить $d\; \{\backslash \; displaystyle\; d\}$дефектных элементов среди $n\; \{\backslash \; displaystyle\; n\}$элементов с нулевой вероятностью ошибки с помощью любого алгоритма группового тестирования. Для того же количества, но с ограничением, что алгоритм является неадаптивным, обозначение $t\; ¯\; (d,\; n)\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{t\}\}\; (d,\; n)\}$

Общие границы

Поскольку всегда можно прибегнуть к индивидуальному тестированию, установив $S\; j\; =\; \{j\}\; \{\backslash \; displaystyle\; S\_\; \{j\}\; =\; \backslash \; \{j\; \backslash \}\}$для каждого $1\; \le \; j\; \le \; n\; \{\backslash \; displaystyle\; 1\; \backslash \; leq\; j\; \backslash \; leq\; n\}$должно быть так, что $t\; ¯\; (d,\; n)\; \le \; n\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{t\}\}\; (d,\; n)\; \backslash \; leq\; n\}$. Кроме того, поскольку любая процедура неадаптивного тестирования может быть записана как адаптивный алгоритм, просто выполняя все тесты без учета их результата, $t\; (d,\; n)\; \le \; t\; ¯\; (d,\; n)\; \{\backslash \; displaystyle\; t\; (\; d,\; n)\; \backslash \; leq\; \{\backslash \; bar\; \{t\}\}\; (d,\; n)\}$. Наконец, когда $0\; \ne \; d\; \ne \; n\; \{\backslash \; displaystyle\; 0\; \backslash \; neq\; d\; \backslash \; neq\; n\}$, есть по крайней мере один элемент, дефектность которого должна быть определена (по крайней мере, одним тестом), и поэтому $1\; \le \; T\; (d,\; n)\; \{\backslash \; displaystyle\; 1\; \backslash \; leq\; t\; (d,\; n)\}$.

В итоге (если принять $0\; \ne \; d\; \ne \; n\; \{\backslash \; displaystyle\; 0\; \backslash \; neq\; d\; \backslash \; neq\; n\; \}$), $1\; \le \; t\; (d,\; n)\; \le \; t\; ¯\; (d,\; n)\; \le \; n\; \{\backslash \; displaystyle\; 1\; \backslash \; leq\; t\; (d,\; n)\; \backslash \; leq\; \{\backslash \; bar\; \{t\}\; \}\; (d,\; n)\; \backslash \; leq\; n\}$.

Нижняя граница информации

Нижняя граница количества необходимых тестов может быть описана с использованием понятия пространства выборки, обозначенного $S\; \{\backslash \; displaystyle\; \{\; \backslash \; mathcal\; \{S\}\}\}$, который представляет собой просто набор возможных размещений дефектных элементов. Для любой задачи группового тестирования с пространством выборок $S\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{S\}\}\}$и любого алгоритма группового тестирования можно показать, что $t\; \ge \; \lceil \; log\; 2\; \; |\; S\; |\; \rceil \; \{\backslash \; displaystyle\; t\; \backslash \; geq\; \backslash \; lceil\; \backslash \; log\; \_\; \{2\}\; \{|\; \{\backslash \; mathcal\; \{S\}\}\; |\}\; \backslash \; rceil\}$, где $t\; \{\backslash \; displaystyle\; t\}$- минимальное количество тестов, необходимых для выявления всех дефектов с нулевой вероятностью ошибки. Это называется нижней границей информации. Эта оценка выводится из того факта, что после каждого теста $S\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{S\}\}\}$разбивается на два непересекающихся подмножества, каждое из которых соответствует одному из двух возможных результатов тест.

Однако сама по себе нижняя граница информации обычно недостижима даже для небольших задач. Это связано с тем, что разделение $S\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{S\}\}\}$не является произвольным, поскольку оно должно быть осуществимо с помощью некоторого теста.

Фактически, нижняя граница информации может быть обобщена на случай, когда существует ненулевая вероятность того, что алгоритм совершит ошибку. В этой форме теорема дает нам верхнюю границу вероятности успеха, основанную на количестве тестов. Для любого алгоритма группового тестирования, который выполняет $t\; \{\backslash \; displaystyle\; t\}$тесты, вероятность успеха $P\; (успех)\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{P\}\; (\{\backslash \; textrm\; \{\; успех\}\})\}$, удовлетворяет $P\; (успех)\; \le \; t\; /\; log\; 2\; \; (nd)\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{P\}\; (\{\backslash \; textrm\; \{success\}\})\; \backslash \; leq\; t\; /\; \backslash \; log\; \_\; \{2\}\; \{n\; \backslash \; choose\; d\}\}$. Это может быть усилено до: $P\; (успех)\; \le \; 2\; t\; (nd)\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{P\}\; (\{\backslash \; textrm\; \{success\}\})\; \backslash \; leq\; \{\backslash \; frac\; \{2\; ^\; \{t\}\}\; \{n\; \backslash \; choose\; d\}\}\}$.

Представление неадаптивных алгоритмов

Типичная установка для группового тестирования. Неадаптивный алгоритм сначала выбирает матрицу $M\; \{\backslash \; displaystyle\; M\}$, а затем получает вектор y . Тогда задача состоит в том, чтобы найти оценку для x.

. Алгоритмы для неадаптивного группового тестирования состоят из двух отдельных фаз. Во-первых, решается, сколько тестов выполнить и какие элементы включить в каждый тест. На втором этапе, который часто называют этапом декодирования, результаты каждого группового теста анализируются, чтобы определить, какие элементы могут быть дефектными. Первый этап обычно кодируется в матрице следующим образом.

• Предположим, что процедура неадаптивного группового тестирования для $n\; \{\backslash \; displaystyle\; n\}$элементов состоит из тестов $S\; 1,\; S\; 2,\dots ,\; S\; t\; \{\backslash \; displaystyle\; S\_\; \{1\},\; S\_\; \{2\},\; \backslash \; dots,\; S\_\; \{t\}\}$для некоторых $t\; \in \; N\; \ge \; 0\; \{\backslash \; displaystyle\; t\; \backslash \; in\; \backslash \; mathbb\; \{N\}\; \_\; \{\backslash \; geq\; 0\}\}$. Матрица тестирования для этой схемы - это двоичная матрица $t\; \times \; n\; \{\backslash \; displaystyle\; t\; \backslash \; times\; n\}$, $M\; \{\backslash \; displaystyle\; M\}$, где $(M)\; ij\; =\; 1\; \{\backslash \; displaystyle\; (M)\; \_\; \{ij\}\; =\; 1\}$тогда и только тогда, когда $j\; \in \; S\; i\; \{\backslash \; displaystyle\; j\; \backslash \; in\; S\_\; \{i\}\}$(в противном случае - ноль).

Таким образом, каждый столбец $M\; \{\backslash \; displaystyle\; M\}$представляет элемент, а каждая строка представляет тест с $1\; \{\; \backslash \; displaystyle\; 1\}$в записи $(i,\; j)\; -th\; \{\backslash \; displaystyle\; (i,\; j)\; \{\backslash \; textrm\; \{-th\}\}\}$, указывающей, что $i\; -й\; \{\backslash \; displaystyle\; i\; \{\backslash \; textrm\; \{-th\}\}\}$тест включал $j\; -th\; \{\backslash \; displaystyle\; j\; \{\backslash \; textrm\; \{-th\}\}\}$и $0\; \{\backslash \; displaystyle\; 0\}$, указывающее на обратное.

А также вектор $x\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\}$(длины $n\; \{\backslash \; displaystyle\; n\}$), который описывает неизвестный дефектный набор, обычно вводят вектор результатов, который описывает результаты каждого теста.

• Пусть $t\; \{\backslash \; displaystyle\; t\}$будет количеством тестов, выполненных неадаптивным алгоритмом. Вектор результата, $y\; =\; (y\; 1,\; y\; 2,\dots ,\; yt)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\; =\; (y\_\; \{1\},\; y\_\; \{2\},\; \backslash \; dots,\; y\_\; \{t\})\}$, является двоичным вектором длины $t\; \{\backslash \; displaystyle\; t\}$(то есть $y\; \in \; \{0,\; 1\}\; t\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\; \backslash \; in\; \backslash \; \{0,1\; \backslash \}\; ^\; \{t\}\}$) так, что $yi\; =\; 1\; \{\backslash \; displaystyle\; y\_\; \{i\}\; =\; 1\}$тогда и только тогда, когда результат теста $i\; -th\; \{\backslash \; displaystyle\; i\; \{\backslash \; textrm\; \{-th\}\}\}$был положительным (т. е. содержал по крайней мере один дефект).

С этими определениями не- адаптивную задачу можно переформулировать следующим образом: сначала выбирается тестовая матрица $M\; \{\backslash \; displaystyle\; M\}$, затем вектор $y\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\}$возвращается. Тогда задача состоит в том, чтобы проанализировать $y\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\}$, чтобы найти некоторую оценку для $x\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\}$.

в простейшем шумном в случае, когда существует постоянная вероятность, $q\; \{\backslash \; displaystyle\; q\}$, что групповой тест даст ошибочный результат, рассматривается случайный двоичный вектор, $v\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\}$, где каждая запись имеет вероятность $q\; \{\backslash \; displaystyle\; q\}$быть $1\; \{\backslash \; displaystyle\; 1\}$, иначе - $0\; \{\backslash \; displaystyle\; 0\}$. Тогда возвращается вектор $y\; ^\; =\; y\; +\; v\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{y\}\}\}\; =\; \backslash \; mathbf\; \{y\}\; +\; \backslash \; mathbf\; \{v\}\}$, с обычным сложением $(Z\; /\; 2\; Z)\; n\; \{\backslash \; displaystyle\; (\backslash \; mathbb\; \{Z\}\; /\; 2\; \backslash \; mathbb\; \{Z\})\; ^\; \{n\}\}$(эквивалентно это элемент- разумная операция XOR ). Шумный алгоритм должен оценивать $x\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\}$с использованием $y\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{y\}\}\}\}$(то есть без прямого знания $y\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\}$).

Границы для неадаптивных алгоритмов

Матричное представление позволяет доказать некоторые границы для не- адаптивное групповое тестирование. Этот подход отражает подход многих детерминированных планов, где рассматриваются $d\; \{\backslash \; displaystyle\; d\}$-разделимые матрицы, как определено ниже.

• Двоичная матрица, $M\; \{\backslash \; displaystyle\; M\}$, называется $d\; \{\backslash \; displaystyle\; d\}$-разделимостью, если каждая логическая сумма (логическое ИЛИ) любого $d\; \{\backslash \; displaystyle\; d\}$его столбцов различны. Кроме того, запись $d\; ¯\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{d\}\}\}$-separable указывает, что каждая сумма любого из до $столбцы\; d\; \{\backslash \; displaystyle\; d\}$из $M\; \{\backslash \; displaystyle\; M\}$отличаются (это не то же самое, что $M\; \{\backslash \; displaystyleM\}$быть $k\; \{\backslash \; displaystyle\; k\}$-разделимым для каждого $k\; \le \; d\; \{\backslash \; displaystyle\; k\; \backslash \; leq\; d\}$.)

Когда $M\; \{\backslash \; displaystyle\; M\}$- матрица тестирования, свойство быть $d\; \{\backslash \; displaystyle\; d\}$-разделимостью ($d\; ¯\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{\; d\}\}\}$-separable) эквивалентно способности различать (до) $d\; \{\backslash \; displaystyle\; d\}$дефектные. Однако это не гарантирует, что это будет просто. Более сильное свойство, называемое $d\; \{\backslash \; displaystyle\; d\}$-disjunctness, делает.

• Двоичная матрица $M\; \{\backslash \; displaystyle\; M\}$называется $d\; \{\backslash \; displaystyle\; d\}$-разъединением, если логическая сумма любого $Столбцы\; d\; \{\backslash \; displaystyle\; d\}$не содержат других столбцов. (В этом контексте говорят, что столбец A содержит столбец B, если для каждого индекса, где B имеет 1, A также имеет 1.)

Полезное свойство -разъединения заключаются в том, что при количестве до $d\; \{\backslash \; displaystyle\; d\}$дефектных элементов каждый исправный элемент будет присутствовать по крайней мере в одном тесте с отрицательным результатом. Это означает, что существует простая процедура поиска дефектов: просто удалите все элементы, обнаруженные при отрицательном результате теста.

Используя свойства матриц $d\; \{\backslash \; displaystyle\; d\}$-separable и $d\; \{\backslash \; displaystyle\; d\}$-disjunct, могут быть показано для задачи выявления $d\; \{\backslash \; displaystyle\; d\}$дефектов среди $n\; \{\backslash \; displaystyle\; n\}$всего элементов.

1. Количество тестов, необходимых для асимптотически малая средняя вероятность ошибки масштабируется как $O\; (d\; log\; 2\; \; n)\; \{\backslash \; displaystyle\; O\; (d\; \backslash \; log\; \_\; \{2\}\; n)\}$.
2. Количество тестов, необходимых для асимптотически малой максимальной вероятности ошибка масштабируется как $O\; (d\; 2\; log\; 2\; \; n)\; \{\backslash \; displaystyle\; O\; (d\; ^\; \{2\}\; \backslash \; log\; \_\; \{2\}\; n)\}$.
3. Количество тестов, необходимых для нулевой вероятности ошибки, масштабируется как $O\; (d\; 2\; log\; 2\; \; n\; log\; 2\; \; d)\; \{\backslash \; displaystyle\; O\; \backslash \; left\; (\{\backslash \; frac\; \{d\; ^\; \{2\}\; \backslash \; log\; \_\; \{2\}\; n\}\; \{\backslash \; log\; \_\; \{2\}\; d\}\})\; \backslash \; right)\}$.

Иллюстрация обобщенного алгоритма двоичного разбиения, где имеется 8 дефектных элементов и 135 элементов. Здесь $2\; \alpha \; 1\; =\; 16\; \{\backslash \; displaystyle\; 2\; ^\; \{\backslash \; alpha\; \_\; \{1\}\}\; =\; 16\}$, и первый тест дает отрицательный результат, поэтому каждый элемент считается исправным. Следовательно, осталось 119 элементов, поэтому $2\; \alpha \; 2\; =\; 8\; \{\backslash \; displaystyle\; 2\; ^\; \{\backslash \; alpha\; \_\; \{2\}\}\; =\; 8\}$. Эта вторая группа дает положительный результат, поэтому для поиска дефекта используется двоичный поиск. Как только это будет сделано, весь процесс повторяется, вычисляя новое $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$, используя только те элементы, дефектность которых не была определена.

Обобщенный алгоритм двоичного разделения is an essentially-optimal adaptive group-testing algorithm that finds $d\; \{\backslash displaystyle\; d\}$or fewer defectives among $n\; \{\backslash displaystyle\; n\}$items as follows:

1. If $n\; \le \; 2\; d\; -\; 2\; \{\backslash displaystyle\; n\backslash leq\; 2d-2\}$, test the $n\; \{\backslash displaystyle\; n\}$items individually. Otherwise, set $l\; =\; n\; -\; d\; +\; 1\; \{\backslash displaystyle\; l=n-d+1\}$and $\alpha \; =\; \lfloor \; log\; 2\; \; l\; /\; d\; \rfloor \; \{\backslash displaystyle\; \backslash alpha\; =\backslash lfloor\; \backslash log\; \_\{2\}\{l/d\}\backslash rfloor\; \}$.
2. Test a group of size $2\; \alpha \; \{\backslash displaystyle\; 2^\{\backslash alpha\; \}\}$. If the outcome is negative, every item in the group is declared to be non-defective; set $n\; :=\; n\; -\; 2\; \alpha \; \{\backslash displaystyle\; n:=n-2^\{\backslash alpha\; \}\}$and go to step 1. Otherwise, use a binary search to identify one defective and an unspecified number, called $x\; \{\backslash displaystyle\; x\}$, of non-defective items; set $n\; :=\; n\; -\; 1\; -\; x\; \{\backslash displaystyle\; n:=n-1-x\}$and $d\; :=\; d\; -\; 1\; \{\backslash displaystyle\; d:=d-1\}$. Go to step 1.

The generalised binary-splitting algorithm requires no more than $T\; \{\backslash displaystyle\; T\}$tests where $T\; =\; \{\; n\; n\; \le \; 2\; d\; -\; 2\; (\; \alpha \; +\; 2)\; d\; +\; p\; -\; 1\; n\; \ge \; 2\; d\; -\; 1\; \{\backslash displaystyle\; T=\{\backslash begin\{cases\}nn\backslash leq\; 2d-2\backslash \backslash (\backslash alpha\; +2)d+p-1n\backslash geq\; 2d-1\backslash end\{cases\}\}\}$.

For $n\; /\; d\; \{\backslash displaystyle\; n/d\}$large, it can be shown that $T\; \to \; d\; log\; 2\; \; (\; n\; /\; d)\; \{\backslash displaystyle\; T\backslash rightarrow\; d\backslash log\; \_\{2\}(n/d)\}$, which compares favorably to the $t\; =\; e\; log\; 2\; \; e\; d\; log\; 2\; \; (\; n\; d)\; \{\backslash displaystyle\; t=\{\backslash frac\; \{e\}\{\backslash log\; \_\{2\}e\}\}d\backslash log\; \_\{2\}\backslash left(\{\backslash frac\; \{n\}\{d\}\}\backslash right)\}$tests required for Li's $s\; \{\backslash displaystyle\; s\}$-stage algorithm. In fact, the generalised binary-splitting algorithm is close to optimal in the following sense. When $d\; \ge \; 2\; \{\backslash displaystyle\; d\backslash geq\; 2\}$it can be shown that $T\; -\; B\; I\; (\; d,\; n)\; \le \; (\; d\; -\; 1)\; \{\backslash displaystyle\; T-B\_\{I\}(d,n)\backslash leq\; (d-1)\}$, where $B\; I\; (\; d,\; n)\; =\; \lceil \; log\; 2\; \; \sum \; i\; =\; 0\; d\; (\; n\; i)\; \rceil \; \{\backslash displaystyle\; B\_\{I\}(d,n)=\backslash left\backslash lceil\; \backslash log\; \_\{2\}\backslash sum\; \_\{i=0\}^\{d\}\{n\; \backslash choose\; i\}\backslash right\backslash rceil\; \}$is the information lower bound.

Non-adaptive group-testing algorithms tend to assume that the number of defectives, or at least a good upper bound on them, is known. This quantity is denoted $d\; \{\backslash displaystyle\; d\}$in this section. If no bounds are known, there are non-adaptive algorithms with low query complexity that can help estimat e $d\; \{\backslash \; displaystyle\; d\}$.

Комбинаторное отслеживание ортогонального соответствия (COMP)

Иллюстрация алгоритма COMP. COMP определяет элемент a как дефектный, а элемент b как исправный. Однако он ошибочно отмечает c как дефектный, поскольку он «скрывается» дефектными элементами в каждом тесте, в котором он появляется.

Комбинаторное ортогональное сопоставление преследований, или COMP, представляет собой простой неадаптивный алгоритм группового тестирования, который формирует основу для более сложных алгоритмов, которые следуют в этом разделе.

Сначала для каждой записи матрицы тестирования выбирается iid равным $1\; \{\backslash \; displaystyle\; 1\}$с вероятностью $1\; /\; d\; \{\backslash \; displaystyle\; 1\; /\; d\}$и $0\; \{\backslash \; displaystyle\; 0\}$в противном случае.

Этап декодирования выполняется по столбцам (то есть по элементам). Если все тесты, в которых появляется товар, являются положительными, то товар объявляется дефектным; в противном случае предполагается, что товар исправен. Или, что эквивалентно, если элемент появляется в любом тесте с отрицательным результатом, элемент объявляется исправным; в противном случае предполагается, что товар неисправен. Важным свойством этого алгоритма является то, что он никогда не создает ложных отрицательных результатов, хотя ложноположительных результатов возникает, когда все местоположения с единицами в j-м столбце $M\; \{\backslash \; displaystyle\; M\}$(соответствующие исправному элементу j) «скрыты» столбцами других столбцов, соответствующих дефектным элементам.

Алгоритм COMP требует не более $ed\; (1\; +\; \delta )\; ln\; \; (n)\; \{\backslash \; displaystyle\; ed\; (1+\; \backslash \; delta)\; \backslash \; ln\; (n)\}$тестов иметь вероятность ошибки меньше или равную $n\; -\; \delta \; \{\backslash \; displaystyle\; n\; ^\; \{-\; \backslash \; delta\}\}$. Это находится в пределах постоянного коэффициента нижней границы для указанной выше средней вероятности ошибки.

В шумном случае ослабляется требование исходного алгоритма COMP, согласно которому набор местоположений единиц в любом столбце $M\; \{\backslash \; displ\; aystyle\; M\}$, соответствующему положительному элементу, полностью содержится в наборе единиц в векторе результата. Вместо этого определенное количество «несовпадений» - это количество несовпадений зависит от количества в каждом столбце, так и от параметров шума $q\; \{\backslash \; displaystyle\; q\}$. Этот зашумленный алгоритм COMP требует не более $4,36\; (\delta \; +\; 1\; +\; \delta )\; 2\; (1-2\; q)\; -\; 2\; d\; log\; 2\; \; n\; \{\backslash \; displaystyle\; 4.36\; (\{\backslash \; sqrt\; \{\backslash \; delta\}\}\; +\; \{\backslash \; sqrt\; \{1+\; \backslash \; delta\}\})\; ^\; \{2\}\; (1-2q)\; ^\; \{-\; 2\}\; d\; \backslash \; log\; \_\; \{2\}\; \{n\}\}$тесты для достижения вероятности ошибки не более $n\; -\; \delta \; \{\backslash \; displaystyle\; n\; ^\; \{-\; \backslash \; delta\}\}$.

Определенные дефекты (DD)

Определенные дефекты (DD) расширением алгоритма COMP, который пытается удалить любые ложные срабатывания. Было показано, что гарантии для DD строго превышают таковые для COMP.

На этапе декодирования используется полезное свойство алгоритма COMP: элемент, который COMP объявляет исправным, безусловно, исправен (т. Е. ложных негативов нет). Происходит это следующим образом.

1. Сначала запускается алгоритм COMP, и все исправляются дефекты, которые он обнаруживает, удаляются. Все оставшиеся элементы теперь «возможно неисправны».
2. Затем алгоритм просматривает все положительные тесты. Если элемент обнаруживается как единственный «возможный дефект» в тесте, то он должен быть дефектным, поэтому алгоритм объявляет его дефектным.
3. Предполагается, что все остальные элементы не являются дефектными. Обоснование этого последнего шага исходит из предположения, что количество дефектов намного меньше, чем общее количество элементов.

Обратите внимание, что шаги 1 и 2 не допускают ошибок, поэтому алгоритм может сделать ошибку только в том случае, если он объявляет дефектный элемент не должен быть дефектным. Таким образом, алгоритм DD может создать только ложноотрицательные результаты.

Sequential COMP (SCOMP)

SCOMP (Sequential COMP) - это алгоритм, который использует тот факт, что DD не допускает ошибок до последнего шага, где гарантированы оставшиеся элементы исправный. Пусть набор заявленных дефектов будет $K\; \{\backslash \; displaystyle\; K\}$. Положительный тест называется объясненным с помощью $K\; \{\backslash \; displaystyle\; K\}$, если он содержит хотя бы один элемент в $K\; \{\backslash \; displaystyle\; K\}$. Ключевое наблюдение с помощью SCOMP заключается в том, что набор дефектов, обнаруженных DD, не может найти каждый положительный тест, и что каждый необъяснимый тест должен содержать скрытый дефект.

Алгоритм работает следующим образом.

1. Выполните шаги 1 и 2 алгоритма DD, чтобы получить $K\; \{\backslash \; displaystyle\; K\}$, начальную оценку для набора дефектов.
2. Если $K\; \{\backslash \; displaystyle\; K\}$объясняет каждый положительный тест, завершите алгоритм: $K\; \{\backslash \; displaystyle\; K\}$- окончательная оценка для набора дефектов.
3. Если есть какие-либо необъяснимые тесты, найдите «возможный дефект», который появляется в наибольшем количестве необъяснимых тестов, и объявите его дефектным (то есть добавить его в набор $K\; \{\backslash \; displaystyle\; K\}$). Переходите к шагу 2.

При моделировании было показано, что SCOMP работает близко к оптимальному.

Обобщенность теории группового тестирования позволяет использовать ее во многих приложениях, включая скрининг клонов, обнаружение коротких замыканий; высокоскоростные компьютерные сети; медицинское обследование, количественный поиск, статистика; машинное обучение, секвенирование ДНК; криптография; и судебная экспертиза данных. В этом разделе представлен краткий обзор небольшой подборки этих приложений.

Каналы множественного доступа

Иллюстрация множественного доступа, показывающая успешное сообщение и конфликт сообщений.

A канал множественного доступа - это канал связи, который соединяет сразу несколько пользователей. Каждый пользователь может одновременно передавать и передавать передачу, сигналы сталкиваются и превращаются в неразборчивый шум. Каналы множественного доступа важны для различных приложений, особенно для беспроводных компьютерных сетей и телефонных сетей.

Важная проблема с форматами множественного доступа в том, как назначать время передачи пользователям, чтобы их сообщения не конфликтовали. Простой способ - предоставить каждому свой собственный временной интервал для передачи, что требует $n\; \{\backslash \; displaystyle\; n\}$слотов. (Это называется мультиплексированием с временным разделением, или TDM.) Однако это очень неэффективно, так как оно будет назначать слоты передачи пользователям, которые не могут иметь сообщения, и обычно, что только несколько пользователей захотят передать в любой момент. заданное время - иначе канал с множественным доступом вообще не практичен.

В контексте группового тестирования эта проблема обычно решается путем разделения времени на «эпохи» следующим образом. Пользователь называется «активным», если у него есть сообщение в начале эпохи. (Если сообщение создается в течение эпохи, пользователь становится активным только в начале следующей.) Эпоха заканчивается, когда каждый активный пользователь успешно передал свое сообщение. Тогда проблема состоит в том, чтобы найти всех активных пользователей в заданную эпоху и запланировать для них время передачи (если они еще не сделали это успешно). Здесь тест на группе пользователей соответствует тем пользователям, которые выполняют передачу. Результатом теста является количество пользователей, которые пытались передать, $0,\; 1,\; \{\backslash \; displaystyle\; 0,1,\}$и $2\; +\; \{\backslash \; displaystyle\; 2\; ^\; \{+\}\}$, что соответствует, соответственно, отсутствию активных пользователей, ровно одному активному пользователю (сообщение успешно) или более чем одному активному пользователю (конфликт сообщения). Таким образом, используя алгоритм адаптивного группового тестирования результатов $\{0,\; 1,\; 2\; +\}\; \{\backslash \; displaystyle\; \backslash \; \{0,1,2\; ^\; \{+\}\; \backslash \}\}$, можно определить, какие пользователи хотят передать в эпоху. Затем любому пользователю, который еще не осуществил успешную передачу, теперь может быть назначен интервал для передачи без расточительного назначения времени неактивным пользователям.

Машинное обучение и сжатое распознавание

Машинное обучение - это область компьютерных наук, в которой есть набор программных приложений, таких как классификация ДНК, обнаружение мошенничества и таргетированная реклама. Одним из основных подразделов машинного обучения является проблема «обучения на примерах», где задача состоит в том, чтобы аппроксимировать некоторую неизвестную функцию, когда ей задано ее в некоторых точках. Как указано в этом разделе, эту проблему обучения функциям можно решить с помощью подхода группового тестирования.

В простой версии задачи есть неизвестная функция, $f:\; \{0,\; 1\}\; N\; \to \; \{0,\; 1\}\; \{\backslash \; displaystyle\; f:\; \backslash \; \{0,1\; \backslash \}\; ^\; \{N\}\; \backslash \; to\; \backslash \; \{0,1\; \backslash \}\}$где $f\; (x)\; =\; a\; \cdot \; x\; \{\backslash \; displaystyle\; f\; (\{\backslash \; textbf\; \{x\}\})\; =\; \{\backslash \; textbf\; \{a\}\}\; \backslash \; cdot\; \{\backslash \; textbf\; \{x\}\}\}$и $a\; \in \; \{0,\; 1\}\; N\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{a\}\}\; \backslash \; in\; \backslash \; \{0,1\; \backslash \}\; ^\; \{N\}\}$(с использованием логической арифметики: сложение шифрования ИЛИ, а умножение - логическим И). Здесь $a\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{a\}\}\}$равно '$d\; \{\backslash \; displaystyle\; d\}$sparse', что означает, что не более $d\; \ll \; N\; \{\backslash \; displaystyle\; d\; \backslash \; ll\; N\}$из его записей: $1\; \{\backslash \; displaystyle\; 1\}$. Цель состоит в том, чтобы построить приближение к $f\; \{\backslash \; displaystyle\; f\}$с использованием $t\; \{\backslash \; displaystyle\; t\}$точечных оценок, где $t\; \{\; \backslash \; displaystyle\; t\}$- как можно меньше. (Точное восстановление $f\; \{\backslash \; displaystyle\; f\}$соответствует алгоритмам с нулевыми ошибками, тогда как $f\; \{\backslash \; displaystyle\; f\}$аппроксимируется алгоритмами, не имеющими нулевая вероятность ошибки.)

В этой задаче восстановление $f\; \{\backslash \; displaystyle\; f\}$эквивалентно поиску $a\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{a\}\}\}$. Кроме того, $f\; (p)\; =\; 1\; \{\backslash \; displaystyle\; f\; (\{\backslash \; textbf\; \{p\}\})\; =\; 1\}$тогда и только тогда, когда есть некоторый индекс, $n\; \{\backslash \; displaystyle\; n\}$, где $an\; =\; pn\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{a\}\}\; \_\; \{n\}\; =\; \{\backslash \; textbf\; \{p\}\}\; \_\; \{n\}\; =\; 1\}$. Таким образом, эта проблема аналогична задаче группового тестирования с $d\; \{\backslash \; displaystyle\; d\}$дефектными и $n\; \{\backslash \; displaystyle\; n\}$общими элементами. Записи в $a\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{a\}\}\}$являются дефектными, если они $1\; \{\backslash \; displaystyle\; 1\}$, $p\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{p\}\; \}\}$указывает тест, и тест является положительным тогда и только тогда, когда $f\; (p)\; =\; 1\; \{\backslash \; displaystyle\; f\; (\{\backslash \; textbf\; \{p\}\})\; =\; 1\}$.

На f: CN → C {\ displaystyle f: \ mathbb {C} ^ {N} \ to \ mathbb {C}}, где $f\; (x)\; =\; a\; \cdot \; x\; \{\backslash \; displaystyle\; f\; (\{\backslash \; textbf\; \{x\}\})\; =\; \{\backslash \; textbf\; \{a\}\}\; \backslash \; cdot\; \{\backslash \; textbf\; \{x\}\}\}$. Сжатое зондирование, которое сообщило о своей программе, тестирующей, инсульт.

В сжатом зондировании цель состоит в том, чтобы восстановить сигнал, $v\; \in \; CN\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{v\}\}\; \backslash \; in\; \backslash \; mathbb\; \{C\}\; ^\; \{N\}\}$, выполнив ряд измерений. Эти изменяются вектором как скалярное произведение $v\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{v\}\}\}$с выбранным образом. Цель состоит в том, чтобы использовать небольшое количество измерений, хотя это, как правило, невозможно, если не принято что-то о сигнале. Одно из таких предположений (которое является общим) состоит в том, что они имеют большое количество записей $v\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{v\}\}\}$является значимым, что означает, что они имеют большое количество. Существуют способы измерения скалярными произведениями $v\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{v\}\}\}$, уравнение $M\; v\; =\; q\; \{\backslash \; displaystyle\; M\; \{\backslash \; textbf\; \{v\}\}\; =\; \{\backslash \; textbf\; \{q\}\}\}$, где $M\; \{\backslash \; displaystyle\; M\}$- $t\; \times \; N\; \{\backslash \; displaystyle\; t\; \backslash \; times\; N\}$матрица, который представлен набором выбранных измерений, а $q\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{q\}\}$представляет собой набор результатов измерений. Эта конструкция показывает, что напряжениеое зондирование является разновидностью «непрерывного» группового тестирования.

Основная трудность при распознавании сжатых данных в том, чтобы определить, какие записи являются важными. Как только это будет сделано, существует множество методов для оценки фактических значений записей. К этойчести идентификации можно подойти с помощью простого группового тестирования. Здесь групповой тест дает комплексное число: сумма проверенных записей. Результат теста называется положительным, если он дает комплексное число с большой величиной, что при предположении, что значимые записи редки, указывает на то, что в крайней мере одна значимая запись.

Существуют явные детерминированные конструкции для этого типа комбинаторного алгоритма поиска, требующие $d\; 2\; (log\; 2\; \; log\; 2\; \; N)\; O\; (1)\; \{\backslash \; displaystyle\; d2\; ^\; \{(\backslash \; log\; \_\; \{2\}\; \backslash \; log\; \_\; \{2\}\; N)\; ^\; \{O\; (1)\}\}\}$измерений. Однако, как и в случае с групповым тестированием, они являются субоптимальными, и случайные конструкции (такие как COMP) часто могут восстанавливать $f\; \{\backslash \; displaystyle\; f\}$сублинейно в $N\; \{\backslash \; displaystyle\; N\; \}$.

Дизайн мультиплексного анализа для тестирования COVID19

Во время пандемии, такой как вспышка COVID-19 в 2020 году, тесты на обнаружение вирусов иногда запускаются с использованием неадаптивных групповых тестов. Один из примеров был предоставлен проект Origami Assays, который выпустил проекты группового тестирования с открытым исходным кодом для запуска на лабораторном стандартном 96-луночном планшете.

Бумажный шаблон Origami Assay для дизайна группового тестирования

В лабораторных условиях одна проблема группового тестирования Строительство из смесей может занять много времени и его сложно выполнить вручную. Анализы Origami предоставили образцы для этой задачи с построением, предоставив бумажные шаблоны, которые помогли технику распределять образцы по лункам.

Используя самые большие схемы группового тестирования (XL3), можно было протестировать 1120 образцов в 94 пробирных лунках. Если количество истинно положительных результатов было достаточно низкое, то дополнительное тестирование не требовалось.

См. Также: Список стран, реализующих стратегию пулового тестирования на COVID-19.

Криминалистика данных

Криминалистика данных - это область, посвященная поиску методов для сбора цифровых доказательств преступлений. Такие случаи обычно связаны с изменением злоумышленником данных, документов или баз данных жертвы, в том числе, например, изменение налоговой отчетности, вирус, скрывающий свое присутствие, или похититель данных, изменяющий личные данные.

Обычный инструмент в криминалистика данных - это односторонний криптографический хэш. Функция, которая принимает данные и с помощью труднообратимой процедуры выдает уникальный номер, называемый хешем. Хэши, которые часто намного короче, чем данные, позволяют без необходимости расточить полные копии информации: хэш для текущих данных можно сравнить с прошлым хешем, чтобы определить, есть ли какие-либо изменения произошли. Как узнать, каким образом определить, каким образом, каким образом, каким образом определить, каким образом были установлены данные, нет, каким образом невозможно восстановить, какая часть данных была изменена.

Один из способов обойти это ограничение - сохранить больше хэшей - теперь уже подмножеств структуры - чтобы сузить область, где произошла атака. Однако, чтобы найти точное место атаки с помощью наивного подхода, хэш должен быть сохранен для каждого элемента данных в структуре, что в первую очередь приведет к поражению точки хешей. (Можно также хранить обычную копию данных.) Групповое тестирование можно использовать для значительного уменьшения количества хэшей, которые необходимо сохранить. Тест становится сравнением сохраненных и текущих хэшей, которое является положительным при несоответствии. Это указывает на то, что по крайней мере одна отредактированная база данных (которая в данной модели считается дефектной) содержится в группе, которая сгенерировала текущий хэш.

Фактически, количество необходимых хешей настолько мало, что они могут использоваться вместе с матрицами, чтобы они могли храниться в организационной структуре самих себя. Это означает, что касается памяти, тест можно проводить «бесплатно». (Это верно за исключением мастер-ключа / пароля, который используется для тайного определения хэш-функций.)

Цитаты

Общие ссылки

• Дин-Чжу, Ду; Хван, Фрэнк К. (1993). Комбинаторное групповое тестирование и его приложения. Сингапур: World Scientific. ISBN 978-9810212933.
• Курс Атри Рудры по кодам с исправлением ошибок: комбинаторика, алгоритмы и приложения (весна 2007 г.), лекции 7.
• Курс Атри Рудры по кодам с исправлением ошибок: комбинаторика, алгоритмы и Приложения (весна 2010 г.), Лекции 10, 11, 28, 29
• Ду Д. и Хван Ф. (2006 г.). Объединение дизайнов и неадаптивное групповое тестирование. Бостон: Twayne Publishers.
• Олдридж, М., Джонсон, О. и Скарлетт, Дж. (2019), Групповое тестирование: перспектива теории информации, основы и тенденции® в теории коммуникации и информации: Том. 15: No. 3-4, pp 196-392. doi: 10.1561 / 0100000099
• Эли Порат, Амир Ротшильд: явные неадаптивные комбинаторные схемы группового тестирования. ИКАЛП (1) 2008: 748–759
• Каган, Евгений; Бен-гал, Ирад (2014), «Алгоритм группового тестирования с интерактивным информационным обучением», IIE Transactions, 46 (2): 164–184, doi : 10.1080 / 0740817X.2013.803639, ISSN 0740-817X

• Задача баланса