Ковариантное преобразование

В физике ковариантное преобразование - это правило, определяющее, как определенные объекты, такие как векторы или тензоры, изменяются при изменении базиса. Преобразование, которое описывает новые базисные векторы как линейную комбинацию старых базисных векторов, определяется как ковариантное преобразование . Обычно индексы, идентифицирующие базисные векторы, помещаются как нижние индексы, как и все объекты, которые преобразуются одинаково. Обратным к ковариантному преобразованию является контравариантное преобразование . Когда вектор должен быть инвариантным при изменении базиса, то есть он должен представлять один и тот же геометрический или физический объект, имеющий ту же величину и направление, что и раньше, его компоненты должны преобразовываться в соответствии с правилом контравариантности. Обычно индексы, идентифицирующие компоненты вектора, помещаются как верхние индексы, как и все индексы сущностей, которые преобразуются одинаково. Сумма по индексам попарного совпадения продукта с одинаковыми нижним и верхним индексами инвариантна при преобразовании.

Вектор - это геометрическая величина, в принципе не зависящая (инвариантная) от выбранного базиса. Вектор v задается, скажем, в компонентах v на выбранной основе ei. С другой стороны, скажем, e′j, один и тот же вектор v имеет разные компоненты v 'и

$v\; =\; \sum \; i\; v\; i\; e\; i\; =\; \sum \; j\; v\text{'}\; j\; e\; j\; \text{'}.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; =\; \backslash \; sum\; \_\; \{i\}\; v\; ^\; \{i\}\; \{\backslash \; mathbf\; \{e\}\}\; \_\; \{i\}\; =\; \backslash \; sum\; \_\; \{j\}\; \{v\; \text{'}\backslash ,\}\; ^\; \{j\}\; \backslash \; mathbf\; \{e\}\; \text{'}\_\; \{j\}.\}$

Как вектор, v должен быть инвариантным по отношению к выбранной системе координат и не зависеть от любого выбранного базиса, т.е. его "реальное" направление и величина должны отображаться одинаково независимо от базисных векторов. Если мы выполняем изменение базиса путем преобразования векторов eiв базисные векторы ej, мы также должны гарантировать, что компоненты v преобразуются в новые компоненты v для компенсации.

Необходимое преобразование v называется правилом контравариантного преобразования .

• 

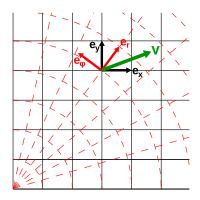
  Вектор v и локальные касательные базисные векторы {ex, ey} и {er, eφ}.

• 

  Координатные представления v.

В показанном примере вектор $v\; =\; \sum \; i\; \in \; \{x,\; y\}\; v\; i\; e\; i\; =\; \sum \; j\; \in \; \{r,\; \varphi \}\; v\; \prime \; j\; e\; j\; \prime .\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; =\; \backslash \; sum\; \_\; \{i\; \backslash \; in\; \backslash \; \{x,\; y\; \backslash \}\}\; v\; ^\; \{i\}\; \{\backslash \; mathbf\; \{e\}\}\; \_\; \{i\}\; =\; \backslash \; sum\; \_\; \{j\; \backslash \; in\; \backslash \; \{\; r,\; \backslash \; phi\; \backslash \}\}\; \{v\; \text{'}\backslash ,\}\; ^\; \{j\}\; \backslash \; mathbf\; \{e\}\text{'}\; \_\; \{j\}.\}$описывается двумя разными системами координат: прямоугольной системой координат (черная сетка) и радиальная система координат (красная сетка). Базовые векторы были выбраны для обеих систем координат: exи eyдля прямоугольной системы координат и erи eφдля радиальной системы координат. Радиальные базисные векторы erи eφпоявляются повернутыми против часовой стрелки по отношению к прямоугольным базисным векторам exи ey. Ковариантное преобразование,, выполняемое для базисных векторов, таким образом, представляет собой вращение против часовой стрелки, вращающееся от первых базисных векторов ко вторым базисным векторам.

Координаты v должны быть преобразованы в новую систему координат, но сам вектор v как математический объект остается независимым от выбранного базиса, появляясь указывать в том же направлении и с той же величиной, инвариантно к изменению координат. Контравариантное преобразование обеспечивает это, компенсируя вращение между различными основаниями. Если мы рассмотрим v из контекста радиальной системы координат, кажется, что он повернут больше по часовой стрелке от базисных векторов erи eφ. по сравнению с тем, как это выглядело относительно прямоугольных базисных векторов exи ey. Таким образом, необходимое контравариантное преобразование в v в этом примере - вращение по часовой стрелке.

• 1 Примеры ковариантного преобразования
  • 1.1 Производная функции преобразуется ковариантно
  • 1.2 Основание векторы преобразуются ковариантно
• 2 Контравариантное преобразование
  • 2.1 Дифференциальные формы преобразуются контравариантно
• 3 Двойные свойства
• 4 Ко- и контравариантные компоненты тензора
  • 4.1 Без координат
  • 4.2 С координатами
• 5 См. также

Производная функции преобразуется ковариантно

Явную форму ковариантного преобразования лучше всего вводить с помощью свойств преобразования производной функции. Рассмотрим скалярную функцию f (например, температуру в определенном месте в пространстве), определенную на множестве точек p, идентифицируемых в данной системе координат $xi,\; i\; =\; 0,\; 1,\dots \; \{\backslash \; displaystyle\; x\; ^\; \{i\},\; \backslash ;\; i\; =\; 0,1,\; \backslash \; dots\}$(такой набор называется многообразием ). Если мы примем новую систему координат $x\; \prime \; j,\; j\; =\; 0,\; 1,\dots \; \{\backslash \; displaystyle\; \{x\; \text{'}\}\; ^\; \{j\},\; j\; =\; 0,1,\; \backslash \; dots\}$, то для для каждого i исходная координата $xi\; \{\backslash \; displaystyle\; \{x\}\; ^\; \{i\}\}$может быть выражена как функция новых координат, поэтому $xi\; (x\; \prime \; j),\; j\; =\; 0,\; 1,\dots \; \{\backslash \; displaystyle\; x\; ^\; \{i\}\; \backslash \; left\; (\{x\; \text{'}\}\; ^\; \{j\}\; \backslash \; right),\; j\; =\; 0,1,\; \backslash \; dots\}$Можно выразить производную от f в старых координатах в новых координатах, используя цепное правило производной, как

$\partial \; f\; \partial \; xi\; =\; \partial \; f\; \partial \; x\; \prime \; j\; \partial \; x\; \prime \; j\; \partial \; xi\; \{\backslash \; displaystyle\; \{\; \backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; \{x\}\; ^\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; \{x\; \text{'}\}\; ^\; \{j\}\}\}\; \backslash ;\; \{\backslash \; frac\; \{\backslash \; partial\; \{\; x\; \text{'}\}\; ^\; \{j\}\}\; \{\backslash \; partial\; \{x\}\; ^\; \{i\}\}\}\}$

Это явная форма правила ковариантного преобразования . В обозначении нормальной производной по координатам иногда используется запятая, как показано ниже:

$f,\; i\; =\; def\; \partial \; f\; \partial \; xi\; \{\backslash \; displaystyle\; f\; \_\; \{,\; i\}\; \backslash \; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{\; =\}\}\; \backslash \; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\; ^\; \{i\}\}\}\}$

где индекс i размещается как нижний индекс из-за ковариантного преобразования.

Базисные векторы преобразуются ковариантно

Вектор может быть выражен в терминах базисных векторов. Для определенной системы координат мы можем выбрать векторы, касательные к координатной сетке. Этот базис называется координатным.

Чтобы проиллюстрировать свойства преобразования, снова рассмотрим набор точек p, идентифицируемых в данной системе координат $xi\; \{\backslash \; displaystyle\; x\; ^\; \{i\}\}$где $i\; =\; 0,\; 1,\dots \; \{\backslash \; displaystyle\; i\; =\; 0,1,\; \backslash \; dots\}$(многообразие ). Скалярная функция f, которая присваивает действительное число каждой точке p в этом пространстве, является функцией координат $f\; (x\; 0,\; x\; 1,\dots )\; \{\backslash \; displaystyle\; f\; \backslash ;\; \backslash \; left\; (x\; ^\; \{0\; \},\; x\; ^\; \{1\},\; \backslash \; точки\; \backslash \; right)\}$. Кривая - это однопараметрический набор точек c, скажем, с параметром кривой λ, c (λ). Касательный вектор v к кривой - это производная $dc\; /\; d\; \lambda \; \{\backslash \; displaystyle\; dc\; /\; d\; \backslash \; lambda\}$вдоль кривой с производной, взятой в точке p под рассмотрение. Обратите внимание, что мы можем видеть касательный вектор v как оператор (производная по направлению ), которая может быть применяется к функции

$v\; [f]\; =\; defdfd\; \lambda \; =\; dd\; \lambda \; f\; (c\; (\lambda ))\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; [f]\; \backslash \; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{=\}\}\; \backslash \; \{\backslash \; frac\; \{df\}\; \{d\; \backslash \; lambda\}\}\; =\; \{\backslash \; frac\; \{d\; \backslash ;\; \backslash ;\}\; \{d\; \backslash \; lambda\}\}\; f\; (c\; (\backslash \; lambda))\}$

Параллель между касательным вектором и оператор также может быть разработан в координатах

$v\; [f]\; =\; dxid\; \lambda \; \partial \; f\; \partial \; xi\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; [f]\; =\; \{\backslash \; frac\; \{dx\; ^\; \{i\}\}\; \{d\; \backslash \; lambda\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\; ^\; \{i\}\}\}\}$

или в терминах операторов $\partial \; /\; \partial \; xi\; \{\backslash \; displaystyle\; \backslash \; partial\; /\; \backslash \; partial\; x\; ^\; \{i\}\}$

$v\; =\; dxid\; \lambda \; \partial \; \partial \; xi\; =\; dxid\; \lambda \; ei\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; =\; \{\backslash \; frac\; \{dx\; ^\; \{i\}\}\; \{d\; \backslash \; lambda\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash ;\; \backslash ;\}\; \{\backslash \; частичный\; x\; ^\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{dx\; ^\; \{i\}\}\; \{d\; \backslash \; lambda\}\}\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\}$

где мы написали $ei\; =\; \partial \; /\; \partial \; xi\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\; =\; \backslash \; partial\; /\; \backslash \; partial\; x\; ^\; \{i\}\}$, касательные векторы к кривым, которые h - это просто сама координатная сетка.

Если мы примем новую систему координат $x\; \prime \; i,\; i\; =\; 0,\; 1,\dots \; \{\backslash \; displaystyle\; \{x\; \text{'}\}\; ^\; \{i\},\; \backslash ;\; i\; =\; 0,1,\; \backslash \; dots\}$тогда для каждого i старая координата $xi\; \{\backslash \; displaystyle\; \{x\; ^\; \{i\}\}\}$может быть выражена как функция новой системы, поэтому $xi\; (x\; \prime \; j),\; j\; =\; 0,\; 1,\dots \; \{\backslash \; displaystyle\; x\; ^\; \{i\}\; \backslash \; left\; (\{x\; \text{'}\}\; ^\; \{j\}\; \backslash \; right),\; j\; =\; 0,1,\; \backslash \; dots\}$Пусть $ei\; \prime \; =\; \partial \; /\; \partial \; x\; \prime \; i\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \text{'}\_\; \{i\}\; =\; \{\backslash \; partial\}\; /\; \{\backslash \; partial\; \{x\text{'}\}\; ^\; \{i\}\}\}$быть базисными касательными векторами в этой новой системе координат. Мы можем выразить $e\; i\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\}$в новой системе, применив правило цепочки к x. В качестве функции координат мы находим следующее преобразование

$ei\; \prime \; =\; \partial \; \partial \; x\; \prime \; i\; =\; \partial \; xj\; \partial \; x\; \prime \; i\; \partial \; \partial \; xj\; =\; \partial \; xj\; \partial \; x\; \prime \; iej\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \text{'}\_\; \{i\; \}\; =\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \{x\; \text{'}\}\; ^\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; x\; ^\; \{j\}\}\; \{\backslash \; partial\; \{x\text{'}\}\; ^\; \{i\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; x\; ^\; \{j\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; x\; ^\; \{j\}\}\; \{\backslash \; partial\; \{x\; \text{'}\}\; ^\; \{i\}\}\}\; \backslash \; mathbf\; \{e\}\; \_\; \{j\}\; \}$

, что на самом деле совпадает с ковариантным преобразованием производной функции.

Компоненты (касательного) векторного преобразования преобразуются другим способом, называемым контравариантным преобразованием. Рассмотрим касательный вектор v и назовем его компоненты $vi\; \{\backslash \; displaystyle\; v\; ^\; \{i\}\}$на основе $ei\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\}$. На другом основании $ei\; \prime \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \text{'}\_\; \{i\}\}$мы называем компоненты $v\; \prime \; i\; \{\backslash \; displaystyle\; \{v\text{'}\}\; ^\; \{i\}\}$, поэтому

$v\; =\; viei\; =\; v\; \prime \; iei\; \prime \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; =\; v\; ^\; \{i\}\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\; =\; \{v\; \text{'}\}\; ^\; \{i\; \}\; \backslash \; mathbf\; \{e\}\; \text{'}\_\; \{i\}\}$

, в котором

$vi\; =\; dxid\; \lambda \; и\; v\; \prime \; i\; =\; dx\; \prime \; id\; \lambda \; \{\backslash \; displaystyle\; v\; ^\; \{i\}\; =\; \{\backslash \; frac\; \{dx\; ^\; \{i\; \}\}\; \{d\; \backslash \; lambda\}\}\; \backslash ;\; \{\backslash \; t\_dv\; \{and\}\}\; \backslash ;\; \{v\; \text{'}\}\; ^\; \{i\}\; =\; \{\backslash \; frac\; \{d\; \{x\text{'}\}\; ^\; \{i\}\}\; \{d\; \backslash \; lambda\}\}\}$

Если выразить новые компоненты в терминах старых, то

$v\; \prime \; i\; =\; dx\; \prime \; id\; \lambda \; =\; \partial \; x\; \prime \; i\; \partial \; xjdxjd\; \lambda \; =\; \partial \; x\; \prime \; i\; \partial \; xjvj\; \{\backslash \; displaystyle\; \{v\; \text{'}\}\; ^\; \{i\}\; =\; \{\backslash \; frac\; \{d\; \{x\; \text{'}\}\; ^\; \{i\}\}\; \{d\; \backslash \; lambda\; \backslash ;\; \backslash ;\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \{x\text{'}\}\; ^\; \{i\}\}\; \{\backslash \; partial\; x\; ^\; \{\; j\}\}\}\; \{\backslash \; frac\; \{dx\; ^\; \{j\}\}\; \{d\; \backslash \; lambda\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \{x\; \text{'}\}\; ^\; \{i\}\}\; \{\backslash \; partial\; x\; ^\; \{j\}\}\}\; \{v\}\; ^\; \{j\}\}$

Это явная форма преобразования, называемого контравариантным преобразованием, и мы отмечаем, что это другое и просто обратное ковариантному правилу. Чтобы отличить их от ковариантных (касательных) векторов, сверху ставится индекс.

Дифференциальные формы преобразуются контравариантно

Пример контравариантного преобразования дается дифференциальной формой df. Для f как функции координат $xi\; \{\backslash \; displaystyle\; x\; ^\; \{i\}\}$, df может быть выражено через $dxi\; \{\backslash \; displaystyle\; dx\; ^\; \{i\}\}$. Дифференциалы dx преобразуются в соответствии с правилом контраварианта, поскольку

$dx\; \prime \; i\; =\; \partial \; x\; \prime \; i\; \partial \; xjdxj\; \{\backslash \; displaystyle\; d\; \{x\; \text{'}\}\; ^\; \{i\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \{x\text{'}\}\; ^\; \{i\}\; \}\; \{\backslash \; partial\; \{x\}\; ^\; \{j\}\}\}\; \{dx\}\; ^\; \{j\}\}$

Сущности, которые преобразуются ковариантно (например, базисные векторы), и сущности, которые преобразуются контравариантно (например, компоненты векторной и дифференциальной форм) «почти одинаковы», но все же они разные. У них есть «двойственные» свойства. То, что стоит за этим, математически известно как двойное пространство, которое всегда сочетается с данным линейным векторным пространством .

Возьмите любое векторное пространство T. Функция f на T называется линейной, если, для любых векторов v, wи скаляра α:

$f\; (v\; +\; w)\; =\; f\; (v)\; +\; f\; (w)\; f\; (\alpha \; v)\; =\; \alpha \; f\; (v)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; f\; (\backslash \; mathbf\; \{v\}\; +\; \backslash \; mathbf\; \{w\})\; =\; f\; (\backslash \; mathbf\; \{v\})\; +\; f\; (\backslash \; mathbf\; \{w\})\; \backslash \backslash \; f\; (\backslash \; alpha\; \backslash \; mathbf\; \{v\})\; =\; \backslash \; alpha\; f\; (\; \backslash \; mathbf\; \{v\})\; \backslash \; end\; \{align\}\}\}$

Простым примером является функция, которая присваивает вектору значение одного из его компонентов (называемая функцией проекции). Он имеет вектор в качестве аргумента и присваивает действительное число, значение компонента.

Все такие скалярнозначные линейные функции вместе образуют векторное пространство, называемое двойным пространством T. Сумма f + g снова является линейной функцией для линейных f и g, а то же самое верно и для скалярного умножения αf.

Учитывая базис $ei\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\}$для T, мы можем определить базис, называемый дуальным базисом для сопряженного пространства естественным образом, взяв набор линейных функций, упомянутых выше: функции проекции. Каждая функция проекции (индексированная ω) производит число 1 при применении к одному из базисных векторов $e\; i\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\}$. Например, $\omega \; 0\; \{\backslash \; displaystyle\; \backslash \; omega\; ^\; \{0\}\}$дает 1 на $e\; 0\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{0\}\}$и ноль в других местах. Применение этой линейной функции $\omega \; 0\; \{\backslash \; displaystyle\; \{\backslash \; omega\}\; ^\; \{0\}\}$к вектору $v\; =\; viei\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; =\; v\; ^\; \{i\}\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\}$, дает (используя его линейность)

$\omega \; 0\; (v)\; =\; \omega \; 0\; (viei)\; =\; vi\; \omega \; 0\; (ei)\; =\; v\; 0\; \{\backslash \; displaystyle\; \backslash \; omega\; ^\; \{0\}\; (\backslash \; mathbf\; \{v\})\; =\; \backslash \; omega\; ^\; \{0\}\; (v\; ^\; \{i\}\; \backslash \; mathbf\; \{e\}\; \_\; \{i\})\; =\; v\; ^\; \{i\}\; \backslash \; omega\; ^\; \{0\}\; (\backslash \; mathbf\; \{e\}\; \_\; \{i\})\; =\; v\; ^\; \{0\}\}$

, поэтому просто значение первой координаты. По этой причине она называется функцией проекции .

. Существует столько же двойственных базисных векторов $\omega \; i\; \{\backslash \; displaystyle\; \backslash \; omega\; ^\; \{i\}\}$, сколько базисных векторов $ei\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\}$, поэтому двойное пространство имеет ту же размерность, что и само линейное пространство. Это «почти то же самое пространство», за исключением того, что элементы двойственного пространства (называемые дуальными векторами ) преобразуются ковариантно, а элементы касательного векторного пространства преобразуются контравариантно.

Иногда вводятся дополнительные обозначения, где действительное значение линейной функции σ на касательном векторе u задается как

$\sigma \; [u]:\; =\; ⟨\sigma ,\; u⟩\; \{\; \backslash \; displaystyle\; \backslash \; sigma\; [\backslash \; mathbf\; \{u\}]:\; =\; \backslash \; langle\; \backslash \; sigma,\; \backslash \; mathbf\; \{u\}\; \backslash \; rangle\}$

где $⟨\sigma ,\; u⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; \backslash \; sigma,\; \backslash \; mathbf\; \{u\; \}\; \backslash \; rangle\}$- действительное число. Это обозначение подчеркивает билинейность формы. Он линейен по σ, так как это линейная функция, и он линейен по u, поскольку это элемент векторного пространства.

Без координат

A тензор типа (r, s) может быть определен как действительная полилинейная функция из r двойственных векторов и s векторов. Поскольку векторы и двойственные векторы могут быть определены независимо от системы координат, тензор, определенный таким образом, не зависит от выбора системы координат.

Обозначение тензора:

$T\; (\sigma ,\dots ,\; \rho ,\; u,\dots ,\; v)\; \equiv \; T\; \sigma \dots \; \rho \; u\dots \; v\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; T\; \backslash \; left\; (\; \backslash \; sigma,\; \backslash \; ldots,\; \backslash \; rho,\; \backslash \; mathbf\; \{u\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{v\}\; \backslash \; right)\; \backslash \backslash \backslash \; Equiv\; \{\}\; \{T\; ^\; \{\backslash \; sigma\; \backslash \; ldots\; \backslash \; rho\}\}\; \_\; \{\backslash \; mathbf\; \{\; u\}\; \backslash \; ldots\; \backslash \; mathbf\; \{v\}\}\; \backslash \; end\; \{align\}\}\}$

для двойственных векторов (дифференциальных форм) ρ, σ и касательных векторов $u,\; v\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\},\; \backslash \; mathbf\; \{v\}\}$. Во второй записи различие между векторами и дифференциальными формами более очевидно.

С координатами

Поскольку тензор линейно зависит от своих аргументов, он полностью определяется, если известны значения на основе $\omega \; i\dots \; \omega \; j\; \{\backslash \; displaystyle\; \backslash \; omega\; ^\; \{\; i\}\; \backslash \; ldots\; \backslash \; omega\; ^\; \{j\}\}$и $ek\dots \; el\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{k\}\; \backslash \; ldots\; \backslash \; mathbf\; \{e\}\; \_\; \{l\}\}$

$T\; (\omega \; я,\dots ,\; \omega \; j,\; ek\dots \; el)\; =\; T\; я\dots \; jk\dots \; l\; \{\backslash \; displaystyle\; T\; (\backslash \; omega\; ^\; \{i\},\; \backslash \; ldots,\; \backslash \; omega\; ^\; \{j\},\; \backslash \; mathbf\; \{e\}\; \_\; \{k\}\; \backslash \; ldots\; \backslash \; mathbf\; \{e\}\; \_\; \{l\})\; =\; \{T\; ^\; \{i\; \backslash \; ldots\; j\}\}\; \_\; \{k\; \backslash \; ldots\; l\}\}$

Числа $T\; i\dots \; jk\dots \; l\; \{\backslash \; displaystyle\; \{T\; ^\; \{i\; \backslash \; ldots\; j\}\}\; \_\; \{k\; \backslash \; ldots\; l\}\}$называются компонентами тензора на выбранном базисе .

Если мы выбираем другой базис (которые линейная комбинация исходного базиса), мы можем использовать линейные свойства тензора, и мы обнаружим, что компоненты тензора в верхних индексах преобразуются как двойственные векторы (так контравариантные), тогда как нижние индексы преобразуются как базис касательной векторы и, таким образом, ковариантны. Для тензора ранга 2 мы можем проверить, что

$A\; \prime \; ij\; =\; \partial \; xl\; \partial \; x\; \prime \; i\; \partial \; xm\; \partial \; x\; \prime \; j\; A\; lm\; \{\backslash \; displaystyle\; \{A\; \text{'}\}\; \_\; \{ij\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; x\; ^\; \{l\}\}\; \{\backslash \; partial\; \{x\; \text{'}\}\; ^\; \{i\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; x\; ^\; \{m\}\}\; \{\backslash \; partial\; \{x\text{'}\}\; ^\; \{j\}\}\}\; A\_\; \{lm\}\}$ковариантный тензор

$A\; \prime \; ij\; =\; \partial \; x\; \prime \; i\; \partial \; xl\; \partial \; x\; \prime \; j\; \partial \; xm\; A\; lm\; \{\backslash \; displaystyle\; \{A\; \text{'}\backslash ,\}\; ^\; \{ij\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \{x\text{'}\}\; ^\; \{i\}\}\; \{\backslash \; partial\; x\; ^\; \{l\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; \{x\; \text{'}\}\; ^\; \{j\}\}\; \{\backslash \; partial\; x\; ^\; \{m\}\}\}\; A\; ^\; \{lm\}\}$контравариантный тензор

Для смешанного ко- и контравариантного тензора ранга 2

$A\; \prime \; ij\; =\; \partial \; x\; \prime \; i\; \partial \; xl\; \partial \; xm\; \partial \; x\; \prime \; j\; A\; lm\; \{\backslash \; displaystyle\; \{A\; \text{'}\backslash ,\}\; ^\; \{i\}\; \{\}\; \_\; \{j\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \{x\; \text{'}\}\; ^\; \{i\}\}\; \{\backslash \; partial\; x\; ^\; \{l\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; x\; ^\; \{m\}\}\; \{\backslash \; partial\; \{x\text{'}\}\; ^\; \{j\}\}\}\; A\; ^\; \{l\}\; \{\}\; \_\; \{m\}\}$смешанный ко- и контравариантный тензор

• Ковариация и контравариантность векторов
• Общая ковариация
• Ковариация Лоренца