Конкуренция Курно

Конкуренция Курно - это экономическая модель, используемая для описания отраслевой структуры, в которой компании конкурируют за объем продукции, который они будут производить, который они определяют независимо друг от друга и в то же время. Он назван в честь Антуана Огюстена Курно (1801–1877), который был вдохновлен наблюдением за конкуренцией в родниковой воде дуополии. Он имеет следующие особенности:

• Существует более одной фирмы, и все фирмы производят однородный продукт, т.е. нет дифференциации продукта ;
• Фирмы не производят сотрудничать, т.е. нет сговора ;
• Фирмы обладают рыночной властью, т.е. решение каждой фирмы о выпуске влияет на цену товара;
• Количество фирм фиксировано;
• Фирмы конкурируют в количествах и выбирают количества одновременно;
• Фирмы экономически рациональны и действуют стратегически, обычно стремясь максимизировать прибыль с учетом решений своих конкурентов.

Важно Предположение этой модели - это «не гипотеза» о том, что каждая фирма стремится максимизировать прибыль, исходя из ожидания, что ее собственное решение о выпуске не повлияет на решения ее конкурентов. Цена - это общеизвестная убывающая функция от общего объема производства. Все фирмы знают $N\; \{\backslash \; displaystyle\; N\}$, общее количество фирм на рынке, и принимают продукцию других как данность. У каждой фирмы есть функция затрат $c\; i\; (q\; i)\; \{\backslash \; displaystyle\; c\_\; \{i\}\; (q\_\; \{i\})\}$. Обычно функции затрат рассматриваются как общеизвестные. Функции затрат могут быть одинаковыми или разными для разных фирм. Рыночная цена устанавливается на таком уровне, что спрос равен общему количеству, произведенному всеми фирмами. Каждая фирма принимает количество, установленное ее конкурентами, как данность, оценивает остаточный спрос и затем ведет себя как монополист.

• 1 История
• 2 Графическое нахождение дуополистического равновесия Курно
• 3 Расчет равновесия
  • 3.1 Пример
• 4 Конкуренция Курно со многими фирмами и теорема Курно
• 5 Последствия
• 6 Бертран против Курно
• 7 См. Также
• 8 Ссылки

Состояние равновесия... поэтому стабильно; то есть, если один из продюсеров, введенный в заблуждение относительно его истинных интересов, временно покинет его, он будет возвращен к нему.

— Антуан Огюстен Курно, Recherches sur les Principes Mathematiques de la Theorie des Richesses (1838), перевод Бэкона (1897).

Антуан Огюстен Курно (1801-1877) впервые изложил свою теорию конкуренции в своем томе 1838 года Recherches sur les Principes Mathematiques de la Theorie des Richesses как способ описания конкуренции с рынком весны. вода, в которой доминируют два поставщика (дуополия ). Эта модель была одной из тех, которые Курно изложил «явно и с математической точностью» в томе. В частности, Курно построил функции прибыли для каждой фирмы, а затем использовал частичное дифференцирование, чтобы построить функцию, представляющую наилучшую реакцию фирмы для заданных (экзогенных) уровней выпуска другой фирмы (фирм). в магазине. Затем он показал, что устойчивое равновесие возникает там, где эти функции пересекаются (т. Е. Одновременное решение функций наилучшего отклика каждой фирмы).

Следствием этого является то, что в равновесии ожидания каждой фирмы относительно того, как будут действовать другие фирмы действие доказано как правильное; когда все раскрыто, ни одна фирма не хочет менять свое решение о выпуске. Эта идея стабильности была позже принята и построена как описание равновесий по Нэшу, из которых равновесия Курно являются подмножеством.

В этом разделе представлен анализ модели с двумя фирмами и постоянными предельными издержками.

$p\; 1\; \{\backslash \; displaystyle\; p\_\; \{1\}\}$= цена фирмы 1, $p\; 2\; \{\backslash \; displaystyle\; p\_\; \{2\}\}$= цена фирмы 2

$q\; 1\; \{\backslash \; displaystyle\; q\_\; \{1\}\}$= количество фирмы 1, $q\; 2\; \{\backslash \; displaystyle\; q\_\; \{2\; \}\}$= количество фирмы 2

$c\; \{\backslash \; displaystyle\; c\}$= предельные издержки, одинаковые для обеих фирм

Равновесные цены будут:

$p\; 1\; =\; p\; 2\; =\; P\; (q\; 1\; +\; q\; 2)\; \{\backslash \; displaystyle\; p\_\; \{1\}\; =\; p\_\; \{2\}\; =\; P\; (q\_\; \{1\}\; +\; q\_\; \{2\})\}$

Это означает, что прибыль фирмы 1 определяется как $\Pi \; 1\; знак\; равно\; q\; 1\; (P\; (q\; 1\; +\; q\; 2)\; -\; c)\; \{\backslash \; displaystyle\; \backslash \; Pi\; \_\; \{1\}\; =\; q\_\; \{1\}\; (P\; (q\_\; \{1\}\; +\; q\_\; \{2\})\; -\; c)\; \}$

• Рассчитайте остаточный спрос фирмы 1: Предположим, фирма 1 считает, что фирма 2 производит количество $q\; 2\; \{\backslash \; displaystyle\; q\_\; \{2\}\}$. Какое оптимальное количество для фирмы 1? Рассмотрим диаграмму 1. Если фирма 1 решает ничего не производить, то цена определяется как $P\; (0\; +\; q\; 2)\; =\; P\; (q\; 2)\; \{\backslash \; displaystyle\; P\; (0\; +\; q\_\; \{2\})\; =\; P\; (\; q\_\; \{2\})\}$. Если фирма 1 производит $q\; 1\; \prime \; \{\backslash \; displaystyle\; q\_\; \{1\}\; \text{'}\}$, то цена определяется как $P\; (q\; 1\; \prime \; +\; q\; 2)\; \{\backslash \; displaystyle\; P\; (q\_\; \{1\; \}\; \text{'}+\; q\_\; \{2\})\}$. В более общем смысле для каждого количества, которое фирма 1 может решить установить, цена задается кривой $d\; 1\; (q\; 2)\; \{\backslash \; displaystyle\; d\_\; \{1\}\; (q\_\; \{2\})\}$. Кривая $d\; 1\; (q\; 2)\; \{\backslash \; displaystyle\; d\_\; \{1\}\; (q\_\; \{2\})\}$называется остаточным спросом фирмы 1; он дает все возможные комбинации количества и цены фирмы 1 для данного значения $q\; 2\; \{\backslash \; displaystyle\; q\_\; \{2\}\}$.

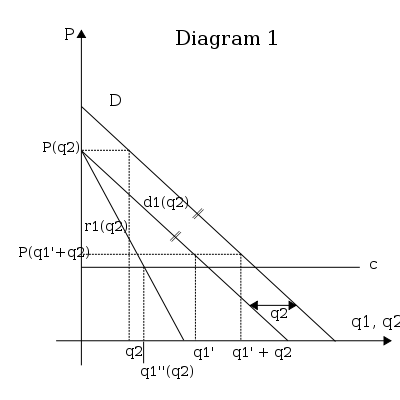
• Определить оптимальный выпуск фирмы 1: для этого мы должны найти где предельный доход равняется предельным затратам. Предполагается, что предельные затраты (c) постоянны. Предельный доход - это кривая - $r\; 1\; (q\; 2)\; \{\backslash \; displaystyle\; r\_\; \{1\}\; (q\_\; \{2\})\}$- с двойным наклоном $d\; 1\; (q\; 2)\; \{\backslash \; displaystyle\; d\_\; \{1\}\; (q\_\; \{2\})\}$и с таким же вертикальным пересечением. Точка, в которой две кривые ($c\; \{\backslash \; displaystyle\; c\}$и $r\; 1\; (q\; 2)\; \{\backslash \; displaystyle\; r\_\; \{1\}\; (q\_\; \{2\})\}$) пересечение соответствует количеству $q\; 1\; ″\; (q\; 2)\; \{\backslash \; displaystyle\; q\_\; \{1\}\; \text{'}\text{'}\; (q\_\; \{2\})\}$. Оптимум для фирмы 1 $q\; 1\; ″\; (q\; 2)\; \{\backslash \; displaystyle\; q\_\; \{1\}\; \text{'}\text{'}\; (q\_\; \{2\})\}$, зависит от того, что, по ее мнению, делает фирма 2. Чтобы найти равновесие, мы выводим оптимум фирмы 1 для других возможных значений $q\; 2\; \{\backslash \; displaystyle\; q\_\; \{2\}\}$. На диаграмме 2 рассматриваются два возможных значения $q\; 2\; \{\backslash \; displaystyle\; q\_\; \{2\}\}$. Если $q\; 2\; =\; 0\; \{\backslash \; displaystyle\; q\_\; \{2\}\; =\; 0\}$, то остаточный спрос первой фирмы фактически является рыночным спросом, $d\; 1\; (0)\; =\; D\; \{\backslash \; displaystyle\; d\_\; \{1\}\; (0)\; =\; D\}$. Оптимальное решение для фирмы 1 - выбрать количество монополист ; $q\; 1\; ″\; (0)\; =\; qm\; \{\backslash \; displaystyle\; q\_\; \{1\}\; \text{'}\text{'}\; (0)\; =\; q\; ^\; \{m\}\}$($qm\; \{\backslash \; displaystyle\; q\; ^\; \{m\}\}$равно монопольное количество). Если бы фирма 2 выбрала количество, соответствующее совершенной конкуренции, $q\; 2\; =\; qc\; \{\backslash \; displaystyle\; q\_\; \{2\}\; =\; q\; ^\; \{c\}\}$так, чтобы $P\; (qc)\; =\; c\; \{\backslash \; displaystyle\; P\; (q\; ^\; \{c\})\; =\; c\}$, тогда оптимумом для фирмы 1 было бы произвести ноль: $q\; 1\; ″\; (qc)\; =\; 0\; \{\; \backslash \; Displaystyle\; q\_\; \{1\}\; \text{'}\text{'}\; (q\; ^\; \{c\})\; =\; 0\}$. Это точка, в которой предельные затраты пересекают предельный доход, соответствующий $d\; 1\; (qc)\; \{\backslash \; displaystyle\; d\_\; \{1\}\; (q\; ^\; \{c\})\}$.

• Можно показать, что, учитывая линейный спрос и постоянных предельных затрат функция $q\; 1\; ″\; (q\; 2)\; \{\backslash \; displaystyle\; q\_\; \{1\}\; \text{'}\text{'}\; (q\_\; \{2\})\}$также является линейной. Поскольку у нас есть две точки, мы можем нарисовать всю функцию $q\; 1\; ″\; (q\; 2)\; \{\backslash \; displaystyle\; q\_\; \{1\}\; \text{'}\text{'}\; (q\_\; \{2\})\}$, см. Диаграмму 3. Примечание. ось графиков изменилась. Функция $q\; 1\; ″\; (q\; 2)\; \{\backslash \; displaystyle\; q\_\; \{1\}\; \text{'}\text{'}\; (q\_\; \{2\})\}$является функцией реакции фирмы 1, она дает Оптимальный выбор фирмы 1 для каждого возможного выбора фирмы 2. Другими словами, он дает фирме 1 выбор с учетом того, что, по ее мнению, делает фирма 2.

• Последним этапом в нахождении равновесия Курно является поиск функции реакции фирмы 2. В этом случае он симметричен фирме 1, поскольку у них одна и та же функция затрат. Равновесие - это точка пересечения кривых реакции. См. Диаграмму 4.

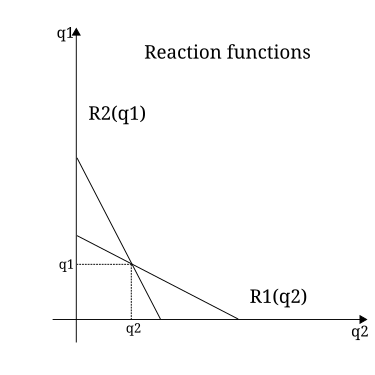
• Модель предсказывает, что фирмы выберут равновесные уровни Нэша уровни выпуска.

В самых общих чертах пусть функция цены для отрасли (дуополии) быть $P\; (q\; 1\; +\; q\; 2)\; \{\backslash \; displaystyle\; P\; (q\_\; \{1\}\; +\; q\_\; \{2\})\}$и фирма $i\; \{\backslash \; displaystyle\; i\; \}$иметь структуру затрат $C\; i\; (qi)\; \{\backslash \; displaystyle\; C\_\; \{i\}\; (q\_\; \{i\})\}$. Чтобы вычислить равновесие по Нэшу, сначала необходимо вычислить функции наилучшего отклика фирм.

Прибыль фирмы i равна выручке за вычетом затрат. Выручка - это произведение цены и количества, а стоимость определяется функцией затрат фирмы, поэтому прибыль (как описано выше): $\Pi \; i\; =\; P\; (q\; 1\; +\; q\; 2)\; \cdot \; qi\; -\; C\; i\; (qi)\; \{\; \backslash \; Displaystyle\; \backslash \; Pi\; \_\; \{я\}\; =\; P\; (q\_\; \{1\}\; +\; q\_\; \{2\})\; \backslash \; cdot\; q\_\; \{i\}\; -C\_\; \{i\}\; (q\_\; \{i\})\}$. Лучший ответ - найти значение $qi\; \{\backslash \; displaystyle\; q\_\; \{i\}\}$, которое максимизирует $\Pi \; i\; \{\backslash \; displaystyle\; \backslash \; Pi\; \_\; \{i\}\}$с учетом $qj\; \{\backslash \; displaystyle\; q\_\; \{j\}\}$, с $i\; \ne \; j\; \{\backslash \; displaystyle\; i\; \backslash \; neq\; j\}$, то есть с учетом некоторой продукции фирмы-оппонента, найден выход, который максимизирует прибыль. Следовательно, максимальное значение $\Pi \; i\; \{\backslash \; displaystyle\; \backslash \; Pi\; \_\; \{i\}\}$относительно $qi\; \{\backslash \; displaystyle\; q\_\; \{i\}\}$должно быть найденный. Сначала возьмем производную от $\Pi \; i\; \{\backslash \; displaystyle\; \backslash \; Pi\; \_\; \{i\}\}$по $qi\; \{\backslash \; displaystyle\; q\_\; \{i\}\}$:

$\partial \; \Pi \; i\; \partial \; qi\; =\; \partial \; п\; (q\; 1\; +\; q\; 2)\; \partial \; qi\; \cdot \; qi\; +\; P\; (q\; 1\; +\; q\; 2)\; -\; \partial \; C\; i\; (qi)\; \partial \; qi\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Pi\; \_\; \{i\}\}\; \{\backslash \; partial\; q\_\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; P\; (q\_\; \{1\}\; +\; q\_\; \{2\})\}\; \{\backslash \; partial\; q\_\; \{i\}\}\}\; \backslash \; cdot\; q\_\; \{i\}\; +\; P\; (q\_\; \{1\}\; +\; q\_\; \{2\})\; -\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{i\}\; (q\_\; \{i\})\}\; \{\backslash \; partial\; q\_\; \{i\}\}\}\}$

Обнуление для максимизации:

$\partial \; \Pi \; i\; \partial \; qi\; Знак\; равно\; \partial \; п\; (q\; 1\; +\; q\; 2)\; \partial \; qi\; \cdot \; qi\; +\; P\; (q\; 1\; +\; q\; 2)\; -\; \partial \; C\; i\; (qi)\; \partial \; qi\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Pi\; \_\; \{i\}\}\; \{\backslash \; partial\; q\_\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; P\; (q\_\; \{1\}\; +\; q\_\; \{2\})\}\; \{\backslash \; partial\; q\_\; \{i\}\}\}\; \backslash \; cdot\; q\_\; \{i\}\; +\; P\; (q\_\; \{1\; \}\; +\; q\_\; \{2\})\; -\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{i\}\; (q\_\; \{i\})\}\; \{\backslash \; partial\; q\_\; \{i\}\}\}\; =\; 0\}$

Значения $qi\; \{\backslash \; displaystyle\; q\_\; \{i\}\}$, которые удовлетворяют этому уравнению, являются лучшими ответами. Равновесие Нэша - это когда оба $q\; 1\; \{\backslash \; displaystyle\; q\_\; \{1\}\}$и $q\; 2\; \{\backslash \; displaystyle\; q\_\; \{2\}\}$являются наилучшими ответами с учетом тех значения $q\; 1\; \{\backslash \; displaystyle\; q\_\; \{1\}\}$и $q\; 2\; \{\backslash \; displaystyle\; q\_\; \{2\}\}$.

Пример

Предположим, что в отрасли следующая структура цены: $P\; (q\; 1\; +\; q\; 2)\; =\; a\; -\; (q\; 1\; +\; q\; 2)\; \{\backslash \; displaystyle\; P\; (q\_\; \{1\}\; +\; q\_\; \{2\})\; =\; a-\; (q\_\; \{1\}\; +\; q\_\; \{2\})\}$Прибыль фирмы $i\; \{\backslash \; displaystyle\; i\}$(со структурой затрат $C\; i\; (qi)\; \{\backslash \; displaystyle\; C\_\; \{i\}\; (q\_\; \{i\})\}$такой, что $\partial \; 2\; C\; i\; (qi)\; \partial \; qi\; 2\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; C\_\; \{i\}\; (q\_\; \{\; i\})\}\; \{\backslash \; partial\; q\_\; \{i\}\; ^\; \{2\}\}\}\; =\; 0\}$и $\partial \; C\; i\; (qi)\; \partial \; qj\; =\; 0,\; j\; \ne \; i\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{i\}\; (q\_\; \{i\})\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\; =\; 0,\; j\; \backslash \; neq\; i\}$для простоты вычислений):

$\Pi \; i\; =\; (a\; -\; (q\; 1\; +\; q\; 2))\; \cdot \; ци\; -\; С\; я\; (ци)\; \{\backslash \; Displaystyle\; \backslash \; Pi\; \_\; \{я\}\; =\; \{\backslash \; bigg\; (\}\; a-\; (q\_\; \{1\}\; +\; q\_\; \{2\})\; \{\backslash \; bigg)\}\; \backslash \; cdot\; q\_\; \{i\}\; -C\_\; \{i\}\; (q\_\; \{i\})\}$

Проблема максимизации решается lves к (из общего случая):

$\partial \; (a\; -\; (q\; 1\; +\; q\; 2))\; \partial \; qi\; \cdot \; qi\; +\; a\; -\; (q\; 1\; +\; q\; 2)\; -\; \partial \; C\; i\; (qi)\; \partial \; qi\; =\; 0\; \{\; \backslash \; Displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \{\backslash \; bigg\; (\}\; a-\; (q\_\; \{1\}\; +\; q\_\; \{2\})\; \{\backslash \; bigg)\}\}\; \{\backslash \; partial\; q\_\; \{i\}\}\}\; \backslash \; cdot\; q\_\; \{i\}\; +\; a-\; (q\_\; \{1\}\; +\; q\_\; \{2\})\; -\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{i\}\; (q\_\; \{i\})\}\; \{\backslash \; partial\; q\_\; \{i\}\}\}\; =\; 0\}$

Без ограничения общности рассмотрим проблема фирмы 1:

$\partial \; (a\; -\; (q\; 1\; +\; q\; 2))\; \partial \; q\; 1\; \cdot \; q\; 1\; +\; a\; -\; (q\; 1\; +\; q\; 2)\; -\; \partial \; C\; 1\; (q\; 1)\; \partial \; q\; 1\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \{\backslash \; bigg\; (\}\; a-\; (q\_\; \{1\}\; +\; q\_\; \{2\})\; \{\backslash \; bigg)\}\}\; \{\backslash \; partial\; q\_\; \{1\}\}\}\; \backslash \; cdot\; q\_\; \{1\}\; +\; a-\; (\; q\_\; \{1\}\; +\; q\_\; \{2\})\; -\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{1\}\; (q\_\; \{1\})\}\; \{\backslash \; partial\; q\_\; \{1\}\}\}\; =\; 0\}$

$\Rightarrow \; -\; q\; 1\; +\; a\; -\; (q\; 1\; +\; q\; 2)\; -\; \partial \; C\; 1\; (q\; 1)\; \partial \; q\; 1\; знак\; равно\; 0\; \{\backslash \; displaystyle\; \backslash \; Rightarrow\; \backslash \; -q\_\; \{1\}\; +\; a-\; (q\_\; \{1\}\; +\; q\_\; \{2\})\; -\; \{\backslash \; frac\; \{\; \backslash \; partial\; C\_\; \{1\}\; (q\_\; \{1\})\}\; \{\backslash \; partial\; q\_\; \{1\}\}\}\; =\; 0\}$

$\Rightarrow \; q\; 1\; =\; a\; -\; q\; 2\; -\; \partial \; C\; 1\; (q\; 1)\; \partial \; q\; 1\; 2\; \{\backslash \; displaystyle\; \backslash \; Rightarrow\; \backslash \; q\_\; \{1\}\; =\; \{\backslash \; frac\; \{a-q\_\; \{2\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{1\}\; (q\_\; \{1\})\}\; \{\backslash \; partial\; q\_\; \{1\}\}\}\}\; \{2\}\; \}\}$

По симметрии:

$\Rightarrow \; q\; 2\; =\; a\; -\; q\; 1\; -\; \partial \; C\; 2\; (q\; 2)\; \partial \; q\; 2\; 2\; \{\backslash \; displaystyle\; \backslash \; Rightarrow\; \backslash \; q\_\; \{2\}\; =\; \{\backslash \; frac\; \{a-q\_\; \{1\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{2\}\; (q\_\; \{2\})\}\; \{\backslash \; partial\; q\_\; \{2\}\}\}\}\; \{2\}\}\}$

Это функции наилучшего реагирования фирм. Для любого значения $q\; 2\; \{\backslash \; displaystyle\; q\_\; \{2\}\}$фирма 1 лучше всего отвечает любым значением $q\; 1\; \{\backslash \; displaystyle\; q\_\; \{1\}\}$что удовлетворяет вышесказанному. В равновесии по Нэшу обе фирмы будут играть наилучшие ответы, поэтому решение вышеуказанных уравнений одновременно. Подставив вместо $q\; 2\; \{\backslash \; displaystyle\; q\_\; \{2\}\}$в лучший ответ фирмы 1:

$q\; 1\; =\; a\; -\; (a\; -\; q\; 1\; -\; \partial \; C\; 2\; (q\; 2)\; \partial \; q\; 2\; 2)\; -\; \partial \; C\; 1\; (q\; 1)\; \partial \; q\; 1\; 2\; \{\backslash \; displaystyle\; \backslash \; q\_\; \{1\}\; =\; \{\backslash \; frac\; \{a-\; \backslash \; left\; (\{\backslash \; frac\; \{a-q\_\; \{1\})\; -\; \{\backslash \; frac\; \{\backslash \; partial)\; C\_\; \{2\}\; (q\_\; \{2\})\}\; \{\backslash \; partial\; q\_\; \{2\}\}\}\}\; \{2\}\}\; \backslash \; right)\; -\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{1\}\; (q\_\; \{1\})\}\; \{\backslash \; partial\; q\_\; \{1\}\}\}\}\; \{2\}\}\}$

$\Rightarrow \; q\; 1\; \ast \; =\; a\; +\; \partial \; C\; 2\; (q\; 2)\; \partial \; q\; 2\; -\; 2\; \ast \; \partial \; C\; 1\; (q\; 1)\; \partial \; q\; 1\; 3\; \{\backslash \; displaystyle\; \backslash \; Rightarrow\; \backslash \; q\_\; \{1\}\; ^\; \{*\}\; =\; \{\backslash \; frac\; \{a\; +\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{2\}\; (q\_\; \{2\})\}\; \{\backslash \; partial\; q\_\; \{2\}\}\}\; -\; 2\; *\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{1\}\; (q\_\; \{1\})\}\; \{\backslash \; partial\; q\_\; \{1\}\}\}\}\; \{3\}\}\}$

$\Rightarrow \; q\; 2\; \ast \; =\; a\; +\; \partial \; C\; 1\; (q\; 1)\; \partial \; q\; 1\; -\; 2\; \ast \; \partial \; C\; 2\; (Q\; 2)\; \partial \; Q\; 2\; 3\; \{\backslash \; Displaystyle\; \backslash \; Rightarrow\; \backslash \; q\_\; \{2\}\; ^\; \{*\}\; =\; \{\backslash \; frac\; \{a\; +\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{1\}\; (q\_\; \{1\})\}\; \{\backslash \; partial\; q\_\; \{1\}\}\}\; -\; 2\; *\; \{\backslash \; frac\; \{\backslash \; partial\; C\_\; \{2\}\; (q\_\; \{2\})\}\; \{\backslash \; partial\; q\_\; \{2\}\}\}\}\; \{3\}\}\}$

Симметричное равновесие по Нэшу находится в $(q\; 1\; *,\; q\; 2\; *)\; \{\backslash \; displaystyle\; (q\_\; \{1\}\; ^\; \{*\},\; q\_\; \{2\}\; ^\; \{*\})\}$. Делая подходящие допущения для частных производных (например, предполагая, что затраты каждой фирмы являются линейной функцией количества и, таким образом, используя наклон этой функции в расчетах), равновесные количества могут быть заменены в предполагаемой структуре цен отрасли $P\; (q\; 1\; +\; q\; 2)\; знак\; равно\; a\; -\; (q\; 1\; +\; q\; 2)\; \{\backslash \; displaystyle\; P\; (q\_\; \{1\}\; +\; q\_\; \{2\})\; =\; a-\; (q\_\; \{1\}\; +\; q\_\; \{2\})\}$для получения равновесной рыночной цены.

Для произвольного количества фирм $N>1\; \{\backslash \; displaystyle\; N>1\}$, количество и цена могут быть получены любым способом аналогично приведенному выше. При линейном спросе и идентичных постоянных предельных издержках равновесные значения следующие:

рыночный спрос; $p\; (q)\; =\; a\; -\; bq\; =\; a\; -\; b\; Q\; =\; p\; (\; Q)\; \{\backslash \; displaystyle\; \backslash \; p\; (q)\; =\; a-bq\; =\; a-bQ\; =\; p\; (Q)\}$

функция затрат; $ci\; (qi)\; =\; cqi\; \{\backslash \; displaystyle\; \backslash \; c\_\; \{i\}\; (q\_\; \{\; i\})\; =\; cq\_\; \{i\}\}$, для всех i

$qi\; =\; Q\; /\; N\; =\; a\; -\; cb\; (N\; +\; 1),\; \{\backslash \; displaystyle\; \backslash \; q\_\; \{i\}\; =\; Q\; /\; N\; =\; \{\backslash \; frac\; \{ac\}\; \{b\; (N\; +\; 1)\}\},\}$

который представляет собой выпуск каждой отдельной фирмы

$\sum \; qi\; =\; N\; q\; =\; N\; (a\; -\; c)\; b\; (N\; +\; 1),\; \{\backslash \; displaystyle\; \backslash \; sum\; q\_\; \{i\}\; =\; Nq\; =\; \{\backslash \; frac\; \{N\; (ac)\}\; \{b\; (N\; +\; 1)\}\},\}$

который является общим объемом производства отрасли

$p\; =\; a\; -\; b\; (N\; q)\; =\; а\; +\; N\; в\; N\; +\; 1,\; \{\backslash \; displaystyle\; \backslash \; p\; =\; ab\; (Nq)\; =\; \{\backslash \; frac\; \{a\; +\; Nc\}\; \{N\; +\; 1\}\},\}$

, которая является рыночной клиринговой ценой, и

$\Pi \; i\; =\; (a\; -\; c\; N\; +\; 1)\; 2\; (1\; b)\; \{\backslash \; displaystyle\; \backslash \; Pi\; \_\; \{i\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{ac\}\; \{N\; +\; 1\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{\; b\}\}\; \backslash \; right)\}$, которая представляет собой прибыль каждой отдельной фирмы.

Теорема Курно утверждает, что в отсутствие фиксированных издержек производства количество фирм на рынке N, стремится к бесконечности, рыночный выпуск Nq переходит на уровень конкуренции, а цена сходится к предельным издержкам.

$lim\; N\; \to \; \infty \; p\; =\; c\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{N\; \backslash \; rightarrow\; \backslash \; infty\}\; p\; =\; c\}$

Следовательно, для многих фирм рынок Курно приближается к рынку с совершенной конкуренцией. Этот результат можно обобщить на случай фирм с различной структурой затрат (при соответствующих ограничениях) и нелинейным спросом.

Однако, когда рынок характеризуется фиксированными издержками производства, мы можем эндогенизировать количество конкурентов, воображающих, что фирмы выходят на рынок, пока их прибыль не станет нулевой. В нашем линейном примере с $N\; \{\backslash \; displaystyle\; N\}$фирмами, когда фиксированные затраты для каждой фирмы равны $F\; \{\backslash \; displaystyle\; F\}$, у нас есть эндогенное число фирм:

$N\; =\; a\; -\; c\; F\; b\; -\; 1\; \{\backslash \; displaystyle\; N\; =\; \{\backslash \; frac\; \{ac\}\; \{\backslash \; sqrt\; \{Fb\}\}\}\; -\; 1\}$

и производство для каждой фирмы, равное:

$q\; =\; F\; bb\; \{\backslash \; displaystyle\; q\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{Fb\}\}\; \{b\}\}\}$

Это равновесие обычно известно как равновесие Курно с эндогенным входом или равновесие Маршалла.

• При дуополии Курно объем производства больше, чем при монополии, но ниже, чем при совершенной конкуренции.
• Цена при дуополии Курно ниже, чем при монополии, но не так низка, как при совершенной конкуренции.
• Согласно этой модели у фирм есть стимул к формированию картеля, что фактически превращает модель Курно в монополию. Картели обычно являются незаконными, поэтому фирмы могут вместо этого молчаливо вступать в сговор, используя самовнушающие стратегии для сокращения выпуска, что при прочих равных поднимет цену и, таким образом, увеличит прибыль для всех участвующих фирм.

Хотя обе модели имеют схожие предположения, они имеют очень разные последствия:

• Поскольку модель Бертрана предполагает, что фирмы конкурируют по цене, а не по объему выпуска, она предсказывает, что дуополия достаточно, чтобы снизить цены до уровня предельных издержек, а это означает, что дуополия приведет к совершенной конкуренции.
• Ни одна из моделей не обязательно «лучше». Точность прогнозов каждой модели будет варьироваться от отрасли к отрасли, в зависимости от близости каждой модели к ситуации в отрасли.
• Если мощность и объем производства можно легко изменить, Бертран - лучшая модель дуопольной конкуренции.. Если объем производства и мощность трудно регулировать, то модель Курно, как правило, лучше.
• При определенных условиях модель Курно может быть преобразована в двухэтапную модель, где на первом этапе фирмы выбирают мощности, а в во-вторых, они конкурируют по моде Бертрана.

Однако по мере того, как количество фирм увеличивается до бесконечности, модель Курно дает тот же результат, что и модель Бертрана: рыночная цена снижается до уровня предельных издержек.

• Агрегированная игра
• Конкуренция Бертрана
• Модель Бертрана – Эджворта
• Предполагаемый вариант
• Теория игр
• Равновесие Нэша
• Конкуренция Штакельберга
• Молчаливый сговор

• Холт, Чарльз. Игры и стратегическое поведение (версия PDF), PDF
• Тироль, Жан. The Theory of Industrial Organization, MIT Press, 1988.
• Oligoply Theory made Simple, глава 6 из Surfing Economics от Huw Dixon.