Доказательства тригонометрических тождеств

редактировать

Доказаны основные тригонометрические тождества между тригонометрическими функциями, в основном с использованием геометрии прямоугольный треугольник. Для получения информации о больших и отрицательных углах см. Тригонометрические функции.

Содержание

1 Элементарные тригонометрические тождества
- 1.1 Определения
- 1.2 Тождества отношения
- 1.3 Дополнительные тождества углов
- 1.4 Пифагоровы тождества
- 1.5 Идентичность суммы углов
  - 1.5.1 Синус
  - 1.5.2 Косинус
  - 1.5.3 Тангенс и котангенс
- 1.6 Идентичность двойного угла
- 1.7 Идентичность половинного угла
- 1.8 Разное - тождество тройного касательного
- 1.9 Прочее - тождество тройного котангенса
- 1.10 Сумма тождеств продукта
  - 1.10.1 Доказательство тождеств синуса
  - 1.10.2 Доказательство тождеств косинуса
- 1.11 Неравенства
2 Идентичности, связанные с исчислением
- 2.1 Предварительные сведения
- 2.2 Идентичность синуса и углового отношения
- 2.3 Идентичность косинуса и углового отношения
- 2.4 Идентичность косинуса и квадрата углового отношения
- 2.5 Доказательство сочетания триггерного и обратного тригонометрические функции
3 См. также
4 Примечания
5 Ссылки

Элементарные тригонометрические тождества

Определения

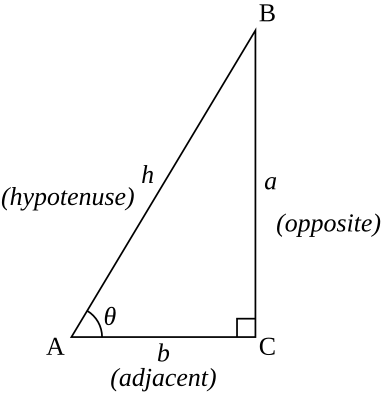
Тригонометрия etric функции определяют отношения между длинами сторон и внутренними углами прямоугольного треугольника. Например, синус угла θ определяется как длина противоположной стороны, деленная на длину гипотенузы.

Шесть тригонометрических функций определены для каждого действительного числа, за исключением некоторых из них для углов, которые отличаются от 0 на кратный прямой угол (90 °). Ссылаясь на диаграмму справа, шесть тригонометрических функций θ для углов, меньших прямого угла:

sin ⁡ θ = противоположная гипотенуза = ah {\ displaystyle \ sin \ theta = {\ frac {\ mathrm {напротив }} {\ mathrm {гипотенуза}}} = {\ frac {a} {h}}}

\sin \theta ={\frac {{\mathrm {opposite}}}{{\mathrm {hypotenuse}}}}={\frac {a}{h}}

cos ⁡ θ = смежнаягипотенуза = bh {\ displaystyle \ cos \ theta = {\ frac {\ mathrm {смежный}} {\ mathrm {гипотенуза}}} = {\ frac {b} {h}}}

\cos \theta ={\frac {{\mathrm {adjacent}}}{{\mathrm {hypotenuse}}}}={\frac {b}{h}}

загар ⁡ θ = противоположный смежный = ab {\ displaystyle \ tan \ theta = {\ frac {\ mathrm {напротив}} {\ mathrm {смежный}} = {\ frac {a} {b}}}

\ tan \ theta = {\ frac {{\ mathrm {напротив}}} {{\ mathrm {смежный}}}} = {\ frac {a} {b}}

детская кроватка ⁡ θ = смежная противоположная = ba {\ displaystyle \ cot \ theta = {\ frac {\ mathrm {смежная}} {\ mathrm { напротив}}} = {\ frac {b} {a}}}

\cot \theta ={\frac {{\mathrm {adjacent}}}{{\mathrm {opposite}}}}={\frac {b}{a}}

сек ⁡ θ = hypotenuseadjacent = hb {\ displaystyle \ sec \ theta = {\ frac {\ mathrm {hypotenuse}} {\ mathrm {смежный} }} = {\ frac {h} {b}}}

\ sec \ theta = {\ frac {{\ mathrm {hypotenuse}}} {{\ mathrm {смежный}}}} = {\ frac {h} {b}}

csc ⁡ θ = hypotenuseopposite = ha {\ displaystyle \ csc \ theta = {\ frac {\ mathrm {hypotenuse}} {\ mat hrm {напротив}}} = {\ frac {h} {a}}}

\csc \theta ={\frac {{\mathrm {hypotenuse}}}{{\mathrm {opposite}}}}={\frac {h}{a}}

Тождества отношения

В случае углов, меньших прямого, следующие идентичности являются прямым следствием приведенных выше определений посредством тождество деления

ab = (ah) (bh). {\ displaystyle {\ frac {a} {b}} = {\ frac {\ left ({\ frac {a} {h}} \ right)} {\ left ({\ frac {b} {h}} \ right)}}.}

{\frac {a}{b}}={\frac {\left({\frac {a}{h}}\right)}{\left({\frac {b}{h}}\right)}}.

Они остаются действительными для углов больше 90 ° и для отрицательных углов.

загар ⁡ θ = противоположный смежный = (противоположная гипотенуза) (смежная гипотенуза) = грех ⁡ θ cos ⁡ θ {\ displaystyle \ tan \ theta = {\ frac {\ mathrm {напротив}} {\ mathrm {смежный}}} = { \ frac {\ left ({\ frac {\ mathrm {напротив}} {\ mathrm {hypotenuse}}} \ right)} {\ left ({\ frac {\ mathrm {смежный}} {\ mathrm {hypotenuse}}} \ right)}} = {\ frac {\ sin \ theta} {\ cos \ theta}}}

\tan \theta ={\frac {{\mathrm {opposite}}}{{\mathrm {adjacent}}}}={\frac {\left({\frac {{\mathrm {opposite}}}{{\mathrm {hypotenuse}}}}\right)}{\left({\frac {{\mathrm {adjacent}}}{{\mathrm {hypotenuse}}}}\right)}}={\frac {\sin \theta }{\cos \theta }}

детская кроватка ⁡ θ = смежная противоположная = (смежная смежная) (противоположная смежная) = 1 загар ⁡ θ = cos ⁡ θ sin ⁡ θ {\ Displaystyle \ cot \ theta = {\ frac {\ mathrm {смежный}} {\ mathrm {противоположный}}} = {\ frac {\ left ({\ frac {\ mathrm {смежный}}} {\ mathrm {смежный} }} \ right)} {\ left ({\ frac {\ mathrm {напротив}} {\ mathrm {смежный}}} \ right)}} = {\ frac {1} {\ tan \ theta}} = {\ гидроразрыв {\ cos \ theta} {\ sin \ theta}}}

\cot \theta =\frac{\mathrm{adjacent}}{\mathrm{opposite}} = \frac { \left( \frac{\mathrm{adjacent}}{\mathrm{adjacent}} \right) } { \left( \frac {\mathrm{opposite}}{\mathrm{adjacent}} \right) } = \frac {1}{\tan \theta} = \frac {\cos \theta}{\sin \theta}

сек ⁡ θ = 1 cos ⁡ θ = гипотенуза, прилегающая {\ displaystyle \ sec \ theta = {\ frac {1} {\ cos \ theta}} = {\ frac {\ mathrm {hypotenuse}} {\ mathrm {прил. acent}}}}

\ sec \ theta = {\ frac {1} {\ cos \ theta}} = {\ frac {{\ mathrm {hypotenuse}}} {{\ mathrm {смежный}}}}

csc ⁡ θ = 1 sin ⁡ θ = hypotenuseopposite {\ displaystyle \ csc \ theta = {\ frac {1} {\ sin \ theta}} = {\ frac {\ mathrm {hypotenuse}} {\ mathrm {напротив}}}}

\ csc \ theta = {\ frac {1} {\ sin \ theta}} = {\ frac {{\ mathrm {hypotenuse}}} {{\ mathrm { напротив}}}}

загар ⁡ θ = противоположный смежный = (противоположный × противоположный гипотенуза × смежный) (смежный × противоположный гипотенуза × смежный) = (гипотенуза напротив) (противоположный гипотенуза) = сек ⁡ θ csc ⁡ θ {\ displaystyle \ загар \ theta = {\ frac {\ mathrm {напротив}} {\ mathrm {прилегающий}}} = {\ frac {\ left ({\ frac {\ mathrm {напротив} \ times \ mathrm {hypotenuse}} {\ mathrm {противоположно} \ раз \ mathrm {прилегающий}}} \ right)} {\ left ({\ frac {\ mathrm {прилегающий} \ times \ mathrm {hypotenuse}} {\ mathrm {противоположный} \ times \ mathrm {прилегающий} }} \ right)}} = {\ frac {\ left ({\ frac {\ mathrm {hypotenuse}} {\ mathrm {смежный}}} \ right)} {\ left ({\ frac {\ mathrm {hypotenuse}) } {\ mathrm {напротив}}} \ right)}} = {\ frac {\ sec \ theta} {\ csc \ theta}}}

\tan \theta = \frac{\mathrm{opposite}}{\mathrm{adjacent}} = \frac{\left(\frac{\mathrm{opposite} \times \mathrm{hypotenuse}}{\mathrm{opposite} \times \mathrm{adjacent}} \right) } { \left( \frac {\mathrm{adjacent} \times \mathrm{hypotenuse}} {\mathrm{opposite} \times \mathrm{adjacent} } \right) } = \frac{\left( \frac{\mathrm{hypotenuse}}{\mathrm{adjacent}} \right)} { \left( \frac{\mathrm{hypotenuse}}{\mathrm{opposite}} \right)} = \frac {\sec \theta}{\csc \theta}

Или

tan ⁡ θ = sin ⁡ θ cos ⁡ θ = (1 csc ⁡ θ) (1 sec ⁡ θ) = (csc ⁡ θ sec ⁡ θ csc ⁡ θ) (csc ⁡ θ sec ⁡ θ sec ⁡ θ) = sec ⁡ θ csc ⁡ θ {\ displaystyle \ tan \ theta = {\ frac {\ sin \ theta} {\ cos \ theta}} = {\ frac {\ left ({\ frac {1} {\ csc \ theta}}) \ right)} {\ left ({\ frac {1} {\ sec \ theta}} \ right)}} = {\ frac {\ left ({\ frac {\ csc \ theta \ sec \ theta} {\ csc \ theta}} \ right)} {\ left ({\ frac {\ csc \ theta \ sec \ theta} {\ sec \ theta}} \ right)}} = {\ frac {\ sec \ theta} {\ csc \ theta}}}

\tan \theta ={\frac {\sin \theta }{\cos \theta }}={\frac {\left({\frac {1}{\csc \theta }}\right)}{\left({\frac {1}{\sec \theta }}\right)}}={\frac {\left({\frac {\csc \theta \sec \theta }{\csc \theta }}\right)}{\left({\frac {\csc \theta \sec \theta }{\sec \theta }}\right)}}={\frac {\sec \theta }{\csc \theta }}

кроватка ⁡ θ = csc ⁡ θ sec ⁡ θ {\ displaystyle \ cot \ theta = {\ frac {\ csc \ theta} {\ sec \ theta}}}

\ cot \ theta = {\ frac {\ csc \ theta} {\ sec \ theta}}

Дополнительные тождества углов

Два угла, сумма которых равна π / 2 радиан (90 градусов), являются дополнительными. На диаграмме углы в вершинах A и B дополняют друг друга, поэтому мы можем поменять местами a и b и изменить θ на π / 2 - θ, получив:

sin ⁡ (π / 2 - θ) = cos ⁡ θ {\ displaystyle \ sin \ left (\ pi / 2- \ theta \ right) = \ cos \ theta}

\sin \left(\pi /2-\theta \right)=\cos \theta

cos ⁡ (π / 2 - θ) = sin ⁡ θ {\ displaystyle \ cos \ left (\ pi / 2- \ тета \ справа) = \ грех \ тета}

\cos \left(\pi /2-\theta \right)=\sin \theta

загар ⁡ (π / 2 - θ) = детская кроватка ⁡ θ {\ Displaystyle \ загар \ влево (\ пи / 2- \ тета \ вправо) = \ кроватка \ theta}

\tan \left(\pi /2-\theta \right)=\cot \theta

детская кроватка ⁡ (π / 2 - θ) = загар ⁡ θ {\ displaystyle \ cot \ left (\ pi / 2- \ theta \ right) = \ tan \ theta}

\cot \left(\pi /2-\theta \right)=\tan \theta

сек ⁡ ( π / 2 - θ) знак равно csc ⁡ θ {\ displaystyle \ sec \ left (\ pi / 2- \ theta \ right) = \ csc \ theta}

\sec \left(\pi /2-\theta \right)=\csc \theta

csc ⁡ (π / 2 - θ) = sec ⁡ θ {\ displaystyle \ csc \ left (\ pi / 2- \ theta \ right) = \ sec \ theta}

\csc \left(\pi /2-\theta \right)=\sec \theta

пифагорейские тождества

Identity 1:

sin 2 ⁡ (x) + cos 2 ⁡ (x) = 1 {\ displaystyle \ sin ^ {2} (x) + \ cos ^ {2} (x) = 1}

\sin^2(x) + \cos^2(x) = 1

Следующие два результата следуют из этого и тождеств отношения. Чтобы получить первое, разделите обе части $sin 2 ⁡ (x) + cos 2 ⁡ (x) = 1 {\ displaystyle \ sin ^ {2} (x) + \ cos ^ {2} (x) = 1}$ $\sin^2(x) + \cos^2(x) = 1$ по $соз 2 ⁡ (x) {\ displaystyle \ cos ^ {2} (x)}$ $\cos ^{2}(x)$ ; второй разделить на $sin 2 ⁡ (x) {\ displaystyle \ sin ^ {2} (x)}$ $\sin^2(x)$ .

tan 2 ⁡ (x) + 1 = sec 2 ⁡ (x) {\ displaystyle \ загар ^ {2} (x) +1 \ = \ sec ^ {2} (x)}

\tan ^{2}(x)+1\ =\sec ^{2}(x)

1 + кроватка 2 ⁡ (x) = csc 2 ⁡ (x) {\ displaystyle 1 \ + \ cot ^ { 2} (x) = \ csc ^ {2} (x)}

1\ +\cot ^{2}(x)=\csc ^{2}(x)

Аналогично

1 + кроватка 2 ⁡ (x) = csc 2 ⁡ (x) {\ displaystyle 1 \ + \ cot ^ {2} (x) = \ csc ^ {2} (x)}

1\ +\cot ^{2}(x)=\csc ^{2}(x)

csc 2 ⁡ (x) - детская кроватка 2 ⁡ (x) = 1 {\ displaystyle \ csc ^ {2} (x) - \ cot ^ {2 } (x) = 1}

\csc ^{2}(x)-\cot ^{2}(x)=1

Идентификатор 2:

Следующее описывает все три взаимные функции.

csc 2 ⁡ (x) + sec 2 ⁡ (x) - детская кроватка 2 ⁡ (x) = 2 + tan 2 ⁡ (x) {\ displaystyle \ csc ^ {2} (x) + \ sec ^ {2 } (x) - \ cot ^ {2} (x) = 2 \ + \ tan ^ {2} (x)}

\csc ^{2}(x)+\sec ^{2}(x)-\cot ^{2}(x)=2\ +\tan ^{2}(x)

Доказательство 2:

См. треугольную диаграмму выше. Обратите внимание, что $a 2 + b 2 = h 2 {\ displaystyle a ^ {2} + b ^ {2} = h ^ {2}}$ $a^{2}+b^{2}=h^{2}$ по теореме Пифагора.

csc 2 ⁡ (x) + sec 2 ⁡ (x) = h 2 a 2 + h 2 b 2 = a 2 + b 2 a 2 + a 2 + b 2 b 2 = 2 + b 2 a 2 + a 2 b 2 {\ displaystyle \ csc ^ {2} (x) + \ sec ^ {2} (x) = {\ frac {h ^ {2}} {a ^ {2}}} + {\ frac {h ^ {2 }} {b ^ {2}}} = {\ frac {a ^ {2} + b ^ {2}} {a ^ {2}}} + {\ frac {a ^ {2} + b ^ {2 }} {b ^ {2}}} = 2 \ + {\ frac {b ^ {2}} {a ^ {2}}} + {\ frac {a ^ {2}} {b ^ {2}} }}

\csc ^{2}(x)+\sec ^{2}(x)={\frac {h^{2}}{a^{2}}}+{\frac {h^{2}}{b^{2}}}={\frac {a^{2}+b^{2}}{a^{2}}}+{\frac {a^{2}+b^{2}}{b^{2}}}=2\ +{\frac {b^{2}}{a^{2}}}+{\frac {a^{2}}{b^{2}}}

Замена соответствующими функциями -

2 + b 2 a 2 + a 2 b 2 = 2 + tan 2 ⁡ (x) + cot 2 ⁡ (x) {\ displaystyle 2 \ + {\ frac { b ^ {2}} {a ^ {2}}} + {\ frac {a ^ {2}} {b ^ {2}}} = 2 \ + \ tan ^ {2} (x) + \ cot ^ {2} (x)}

2\ +{\frac {b^{2}}{a^{2}}}+{\frac {a^{2}}{b^{2}}}=2\ +\tan ^{2}(x)+\cot ^{2}(x)

Перестановка дает:

csc 2 ⁡ (x) + sec 2 ⁡ (x) - cot 2 ⁡ (x) = 2 + tan 2 ⁡ (x) {\ displaystyle \ csc ^ {2} (x) + \ sec ^ {2} (x) - \ cot ^ {2} (x) = 2 \ + \ tan ^ {2} (x)}

\csc ^{2}(x)+\sec ^{2}(x)-\cot ^{2}(x)=2\ +\tan ^{2}(x)

Тождества суммы углов

Синус

Иллюстрация формулы суммы.

Проведите горизонтальную линию (ось x); отметьте начало O. Нарисуйте линию от O под углом $α {\ displaystyle \ alpha}$ $\ alpha$ над горизонтальной линией и вторую линию под углом $β {\ displaystyle \ beta}$ $\ beta$ выше этого; угол между второй линией и осью x равен $α + β {\ displaystyle \ alpha + \ beta}$ $\ alpha + \ beta$ .

Поместите P на линии, определяемой $α + β {\ displaystyle \ alpha + \ beta}$ $\ alpha + \ beta$ на единичном расстоянии от начала координат.

Пусть PQ будет линией, перпендикулярной линии OQ, определенной углом $α {\ displaystyle \ alpha}$ $\ alpha$ , проведенной от точки Q на этой прямой к точке P. $∴ {\ displaystyle \ поэтому}$ $\, следовательно,$ OQP - это прямой угол.

Пусть QA будет перпендикуляром, идущим от точки A на оси x к Q, а PB будет перпендикуляром, идущим от точки B на оси x к P. $∴ {\ displaystyle \ поэтому}$ $\, следовательно,$ OAQ и OBP - прямые углы.

Нарисуйте R на PB так, чтобы QR был параллелен оси x.

Теперь угол $RPQ = α {\ displaystyle RPQ = \ alpha}$ $RPQ=\alpha$ (потому что $OQA = π 2 - α {\ displaystyle OQA = {\ frac {\ pi } {2}} - \ alpha}$ ${\ displaystyle OQA = {\ frac {\ pi} {2}} - \ alpha}$ , что делает $RQO = α, RQP = π 2 - α {\ displaystyle RQO = \ alpha, RQP = {\ frac {\ pi} {2} } - \ alpha}$ $RQO=\alpha,RQP={\frac {\pi }{2}}-\alpha$ и, наконец, $RPQ = α {\ displaystyle RPQ = \ alpha}$ $RPQ=\alpha$ )

RPQ = π 2 - RQP = π 2 - (π 2 - RQO) = RQO = α {\ Displaystyle RPQ = {\ tfrac {\ pi} {2}} - RQP = {\ tfrac {\ pi} {2}} - ({\ tfrac {\ pi} {2}} - RQO) = RQO = \ альфа}

RPQ={\tfrac {\pi }{2}}-RQP={\tfrac {\pi }{2}}-({\tfrac {\pi }{2}}-RQO)=RQO=\alpha

OP = 1 {\ displaystyle OP = 1}

OP=1

PQ = грех ⁡ β {\ displaystyle PQ = \ sin \ beta}

PQ = \ sin \ beta

OQ = cos ⁡ β {\ displaystyle OQ = \ cos \ бета}

OQ=\cos \beta

AQOQ = грех ⁡ α {\ displaystyle {\ frac {AQ} {OQ}} = \ sin \ alpha}

{\frac {AQ}{OQ}}=\sin \alpha

, поэтому

AQ = sin ⁡ α cos ⁡ β {\ displaystyle AQ = \ sin \ alpha \ cos \ beta}

AQ=\sin \alpha \cos \beta

PRPQ = cos ⁡ α {\ displaystyle {\ frac {PR} {PQ}} = \ cos \ alpha}

{\ displaystyle {\ frac {PR} {PQ}} = \ cos \ alpha}

, поэтому

PR знак равно соз ⁡ α грех ⁡ β {\ Displaystyle PR = \ соз \ альфа \ грех \ бета}

PR=\cos \alpha \sin \beta

грех ⁡ (α + β) = PB = RB + PR = AQ + PR = грех ⁡ α cos ⁡ β + c ос ⁡ α грех ⁡ β {\ Displaystyle \ sin (\ альфа + \ бета) = PB = RB + PR = AQ + PR = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta}

\ sin (\ alpha + \ beta) = PB = RB + PR = AQ + PR = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ грех \ бета

Заменяя $- β {\ displaystyle - \ beta}$ $-\beta$ на $β {\ displaystyle \ beta}$ $\ beta$ и используя Symmetry, мы также получаем :

грех ⁡ (α - β) знак равно грех ⁡ α соз ⁡ (- β) + соз ⁡ α грех ⁡ (- β) {\ Displaystyle \ sin (\ альфа - \ бета) = \ грех \ альфа \ соз (- \ бета) + \ соз \ альфа \ грех (- \ бета)}

\sin(\alpha -\beta)=\sin \alpha \cos(-\beta)+\cos \alpha \sin(-\beta)

грех ⁡ (α - β) = грех ⁡ α соз ⁡ β - соз ⁡ α грех ⁡ β {\ Displaystyle \ sin (\ альфа - \ beta) = \ sin \ alpha \ cos \ beta - \ cos \ alpha \ sin \ beta}

\ sin (\ alpha - \ beta) = \ sin \ alpha \ cos \ beta - \ соз \ альфа \ грех \ бета

Другое строгое и гораздо более простое доказательство может быть дано с помощью формулы Эйлера, известной из комплексный анализ. Формула Эйлера:

ei φ = cos ⁡ φ + i sin ⁡ φ {\ displaystyle e ^ {i \ varphi} = \ cos \ varphi + i \ sin \ varphi}

e^{{i\varphi }}=\cos \varphi +i\sin \varphi

Отсюда следует, что для углов $α {\ displaystyle \ alpha}$ $\ alpha$ и $β {\ displaystyle \ beta}$ $\ beta$ имеем:

ei (α + β) = cos ⁡ (α + β) + я грех ⁡ (α + β) {\ Displaystyle е ^ {я (\ альфа + \ бета)} = \ соз (\ альфа + \ бета) + я \ грех (\ альфа + \ бета)}

e^{{i(\alpha +\beta)}}=\cos(\alpha +\beta)+i\sin(\alpha +\beta)

Также используются следующие свойства экспоненциальных функций:

ei (α + β) = ei α ei β = (cos ⁡ α + i sin ⁡ α) (cos ⁡ β + i sin ⁡ β) {\ displaystyle e ^ { я (\ альфа + \ бета)} = е ^ {я \ альфа} е ^ {я \ бета} = (\ соз \ альфа + я \ грех \ альфа) (\ соз \ бета + я \ грех \ бета)}

e^{{i(\alpha +\beta)}}=e^{{i\alpha }}e^{{i\beta }}=(\cos \alpha +i\sin \alpha)(\cos \beta +i\sin \beta)

Оценка произведения:

ei (α + β) = (cos ⁡ α cos ⁡ β - sin ⁡ α sin ⁡ β) + i (sin ⁡ α cos ⁡ β + sin ⁡ β cos ⁡ α) { \ Displaystyle е ^ {я (\ альфа + \ бета)} = (\ соз \ альфа \ соз \ бета - \ грех \ альфа \ грех \ бета) + я (\ грех \ альфа \ соз \ бета + \ грех \ бета \ cos \ alpha)}

e^{{i(\alpha +\beta)}}=(\cos \alpha \cos \beta -\sin \alpha \sin \beta)+i(\sin \alpha \cos \beta +\sin \beta \cos \alpha)

Приравнивание действительной и мнимой частей:

cos ⁡ (α + β) = cos ⁡ α cos ⁡ β - sin ⁡ α грех ⁡ β {\ Displaystyle \ соз (\ альфа + \ бета) = \ соз \ альфа \ соз \ бета - \ грех \ альфа \ грех \ бета}

\cos(\alpha +\beta)=\cos \alpha \cos \beta -\sin \alpha \sin \beta

грех ⁡ (α + β) = грех ⁡ α соз ⁡ β + грех ⁡ β соз ⁡ α {\ displaystyle \ sin (\ alpha + \ beta) = \ sin \ alpha \ cos \ beta + \ sin \ beta \ cos \ alpha}

\ sin (\ alpha + \ beta) = \ sin \ alpha \ cos \ beta + \ sin \ beta \ cos \ alpha

косинус

Использование на рисунке выше

OP = 1 {\ displaystyle OP = 1}

OP=1

PQ = sin ⁡ β {\ displaystyle PQ = \ sin \ beta}

PQ = \ sin \ beta

OQ = cos ⁡ β {\ displaystyle OQ = \ cos \ beta}

OQ=\cos \beta

OAOQ = cos ⁡ α {\ displaystyle {\ frac {OA} {OQ}} = \ cos \ alpha}

{\frac {OA}{OQ}}=\cos \alpha

, поэтому

OA = cos ⁡ α cos ⁡ β { \ displaystyle OA = \ cos \ alpha \ cos \ beta}

{\ displaystyle OA = \ cos \ alpha \ cos \ beta}

RQPQ = sin ⁡ α {\ displaystyle {\ frac {RQ} {PQ}} = \ sin \ alpha}

{\frac {RQ}{PQ}}=\sin \alpha

, поэтому

RQ = грех ⁡ α грех ⁡ β {\ Displaystyle RQ = \ грех \ альфа \ грех \ бета}

RQ=\sin \alpha \sin \beta

соз ⁡ (α + β) = OB = OA - BA = OA - RQ = cos ⁡ α cos ⁡ β - грех ⁡ α грех ⁡ β {\ Displaystyle \ соз (\ альфа + \ бета) = OB = OA-BA = OA-RQ = \ cos \ alpha \ cos \ beta \ - \ sin \ alpha \ sin \ beta}

\cos(\alpha +\beta)=OB=OA-BA=OA-RQ=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta

Заменяя $- β {\ displaystyle - \ beta}$ $-\beta$ на $β {\ displaysty le \ beta}$ $\ beta$ и используя Симметрию, мы также получаем:

cos ⁡ (α - β) = cos ⁡ α cos ⁡ (- β) - sin ⁡ α sin ⁡ (- β), {\ Displaystyle \ соз (\ альфа - \ бета) = \ соз \ альфа \ соз (- \ бета) - \ грех \ альфа \ грех (- \ бета),}

\cos(\alpha -\beta)=\cos \alpha \cos(-\beta)-\sin \alpha \sin(-\beta),

соз ⁡ (α - β) знак равно соз ⁡ α соз ⁡ β + грех ⁡ α грех ⁡ β {\ Displaystyle \ соз (\ альфа - \ бета) = \ соз \ альфа \ соз \ бета + \ грех \ альфа \ грех \ бета}

\cos(\alpha -\beta)=\cos \alpha \cos \beta +\sin \alpha \sin \beta

Кроме того, используя формулы дополнительных углов,

cos ⁡ (α + β) = sin ⁡ (π / 2 - (α + β)) = sin ⁡ ((π / 2 - α) - β) = sin ⁡ (π / 2 - α) соз ⁡ β - соз ⁡ (π / 2 - α) грех ⁡ β = соз ⁡ α соз ⁡ β - грех ⁡ α грех ⁡ β {\ displaystyle {\ begin {align} \ cos (\ alpha + \ beta) = \ sin \ left (\ pi / 2 - (\ alpha + \ beta) \ right) \\ = \ sin \ left ((\ pi / 2- \ alpha) - \ beta \ right) \\ = \ sin \ left (\ pi / 2- \ alpha \ right) \ cos \ beta - \ cos \ left (\ pi / 2- \ alpha \ right) \ sin \ beta \\ = \ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta \\\ end {align}}}

{\begin{aligned}\cos(\alpha +\beta)=\sin \left(\pi /2-(\alpha +\beta)\right)\\=\sin \left((\pi /2-\alpha)-\beta \right)\\=\sin \left(\pi /2-\alpha \right)\cos \beta -\cos \left(\pi /2-\alpha \right)\sin \beta \\=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\\end{aligned}}

Тангенс и котангенс

Из формул синуса и косинуса мы получаем

tan ⁡ (α + β) = грех ⁡ (α + β) соз ⁡ (α + β) знак равно грех ⁡ α соз ⁡ β + соз ⁡ α грех ⁡ β соз ⁡ α соз ⁡ β - грех ⁡ α грех ⁡ β {\ Displaystyle \ загар (\ альфа + \ beta) = {\ frac {\ sin (\ alpha + \ beta)} {\ cos (\ alpha + \ beta)}} = {\ frac {\ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta} {\ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta}}}

\tan(\alpha +\beta)={\frac {\sin(\alpha +\beta)}{\cos(\alpha +\beta)}}={\frac {\sin \alpha \cos \beta +\cos \alpha \sin \beta }{\cos \alpha \cos \beta -\sin \alpha \sin \beta }}

Деление числителя и знаменателя на $cos ⁡ α cos ⁡ β {\ displaystyle \ cos \ alpha \ cos \ beta}$ $\cos \alpha \cos \beta$ , получаем

загар ⁡ (α + β) = загар ⁡ α + загар ⁡ β 1 - загар ⁡ α загар ⁡ β {\ displaystyle \ tan (\ alpha + \ beta) = {\ frac {\ tan \ alpha + \ tan \ beta} {1- \ tan \ alpha \ tan \ beta}}}

\tan(\alpha +\beta)={\frac {\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }}

Вычитание $β {\ displaystyle \ beta}$ $\ beta$ из $α {\ displaystyle \ alpha}$ $\ alpha$ , используя $tan ⁡ (- β) = - tan ⁡ β {\ displaystyle \ tan (- \ beta) = - \ tan \ beta}$ $\tan(-\beta)=-\tan \beta$ ,

загар ⁡ (α - β) = загар ⁡ α + загар ⁡ (- β) 1 - загар ⁡ α загар ⁡ (- β) = загар ⁡ α - загар ⁡ β 1 + загар ⁡ α загар ⁡ β {\ Displaystyle \ tan (\ alpha - \ beta) = {\ frac {\ tan \ alpha + \ tan (- \ beta)} {1- \ tan \ alpha \ tan (- \ beta)}} = {\ frac {\ tan \ alp ha - \ tan \ beta} {1+ \ tan \ alpha \ tan \ beta}}}

\tan(\alpha -\beta)={\frac {\tan \alpha +\tan(-\beta)}{1-\tan \alpha \tan(-\beta)}}={\frac {\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }}

Аналогично из формул синуса и косинуса получаем

cot ⁡ (α + β) = cos ⁡ (α + β) грех ⁡ (α + β) знак равно соз ⁡ α соз ⁡ β - грех ⁡ α грех ⁡ β грех ⁡ α соз ⁡ β + соз ⁡ α грех ⁡ β {\ Displaystyle \ кроватка (\ альфа + \ бета) = { \ frac {\ cos (\ alpha + \ beta)} {\ sin (\ alpha + \ beta)}} = {\ frac {\ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta} {\ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta}}}

\ cot (\ alpha + \ beta) = \ frac {\ cos (\ alpha + \ beta)} {\ sin (\ alpha + \ beta)} = \ frac {\ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta} {\ sin \ alpha \ соз \ бета + \ соз \ альфа \ грех \ бета}

Затем, разделив числитель и знаменатель на $sin ⁡ α sin ⁡ β {\ displaystyle \ sin \ alpha \ sin \ beta }$ $\sin \alpha \sin \beta$ , получаем

детская кроватка ⁡ (α + β) = детская кроватка ⁡ α детская кроватка ⁡ β - 1 детская кроватка ⁡ α + детская кроватка ⁡ β {\ displaystyle \ cot (\ alpha + \ beta) = { \ frac {\ cot \ alpha \ cot \ beta -1} {\ cot \ alpha + \ cot \ beta}}}

\cot(\alpha +\beta)={\frac {\cot \alpha \cot \beta -1}{\cot \alpha +\cot \beta }}

Или, используя $кроватку ⁡ θ = 1 tan ⁡ θ {\ displaystyle \ cot \ theta = {\ frac {1} {\ tan \ theta}}}$ $\ cot \ theta = {\ frac {1} {\ tan \ theta}}$ ,

раскладушка ⁡ (α + β) = 1 - tan ⁡ α tan ⁡ β tan ⁡ α + tan ⁡ β = 1 tan ⁡ α tan ⁡ β - 1 1 загар ⁡ α + 1 загар ⁡ β = детская кроватка ⁡ α детская кроватка ⁡ β - 1 детская кроватка ⁡ α + детская кроватка ⁡ β {\ Displaystyle \ детская кроватка (\ альфа + \ бета) = { \ frac {1- \ tan \ alpha \ tan \ beta} {\ tan \ alpha + \ tan \ beta}} = {\ frac {{\ frac {1} {\ tan \ alpha \ tan \ beta}} - 1 } {{\ frac {1} {\ tan \ alpha}} + {\ frac {1} {\ tan \ beta}}}} = {\ frac {\ cot \ alpha \ cot \ beta -1} {\ cot \ alpha + \ cot \ beta}}}

\cot(\alpha +\beta)={\frac {1-\tan \alpha \tan \beta }{\tan \alpha +\tan \beta }}={\frac {{\frac {1}{\tan \alpha \tan \beta }}-1}{{\frac {1}{\tan \alpha }}+{\frac {1}{\tan \beta }}}}={\frac {\cot \alpha \cot \beta -1}{\cot \alpha +\cot \beta }}

Использование $cot ⁡ (- β) = - cot ⁡ β {\ displaystyle \ cot (- \ beta) = - \ cot \ beta}$ $\cot(-\beta)=-\cot \beta$ ,

cot ⁡ (α - β) знак равно детская кроватка ⁡ α детская кроватка ⁡ (- β) - 1 детская кроватка ⁡ α + детская кроватка ⁡ (- β) = детская кроватка ⁡ α детская кроватка ⁡ β + 1 детская кроватка ⁡ β - детская кроватка ⁡ α {\ displaystyle \ cot (\ альфа - \ бета) = {\ frac {\ cot \ alpha \ cot (- \ beta) -1} {\ cot \ alpha + \ cot (- \ beta)}} = {\ frac {\ cot \ alpha \ cot \ beta +1} {\ cot \ beta - \ cot \ alpha}}}

\cot(\alpha -\beta)={\frac {\cot \alpha \cot(-\beta)-1}{\cot \alpha +\cot(-\beta)}}={\frac {\cot \alpha \cot \beta +1}{\cot \beta -\cot \alpha }}

Тождества с двумя углами

Из тождеств суммы углов получаем

sin ⁡ (2 θ) = 2 грех ⁡ θ соз ⁡ θ {\ Displaystyle \ грех (2 \ тета) = 2 \ грех \ тета \ соз \ тета}

\sin(2\theta)=2\sin \theta \cos \theta

соз ⁡ (2 θ) = соз 2 ⁡ θ - грех 2 ⁡ θ {\ displaystyle \ cos (2 \ theta) = \ cos ^ {2} \ theta - \ sin ^ {2} \ theta}

\cos(2\theta)=\cos ^{2}\theta -\sin ^{2}\theta

Пифагоровы тождества дают две альтернативные формы для последнего из них:

cos ⁡ (2 θ) = 2 cos 2 ⁡ θ - 1 {\ displaystyle \ cos (2 \ theta) = 2 \ cos ^ {2} \ theta -1}

\cos(2\theta)=2\cos ^{2}\theta -1

cos ⁡ (2 θ) = 1-2 грех 2 ⁡ θ {\ displaystyle \ cos (2 \ theta) = 1-2 \ sin ^ {2} \ theta}

\cos(2\theta)=1-2\sin ^{2}\theta

Тождества суммы углов также дают

tan ⁡ (2 θ) = 2 tan ⁡ θ 1 - tan 2 ⁡ θ = 2 cot ⁡ θ - tan ⁡ θ {\ displaystyle \ tan (2 \ theta) = {\ frac {2 \ tan \ theta} {1- \ tan ^ {2} \ theta}} = {\ frac {2} {\ cot \ theta - \ загар \ theta}}}

\tan(2\theta)={\frac {2\tan \theta }{1-\tan ^{2}\theta }}={\frac {2}{\cot \theta -\tan \theta }}

детская кроватка ⁡ (2 θ) = детская кроватка 2 ⁡ θ - 1 2 детская кроватка ⁡ θ = детская кроватка ⁡ θ - загар ⁡ θ 2 {\ displaystyle \ cot (2 \ theta) = {\ frac { \ cot ^ {2} \ theta -1} {2 \ cot \ theta}} = {\ frac {\ cot \ theta - \ tan \ theta} {2}}}

\cot(2\theta)={\frac {\cot ^{2}\theta -1}{2\cot \theta }}={\frac {\cot \theta -\tan \theta }{2}}

Это также можно доказать, используя Формула Эйлера

ei φ = cos ⁡ φ + i sin ⁡ φ {\ displaystyle e ^ {i \ varphi} = \ cos \ varphi + i \ sin \ varphi}

e^{{i\varphi }}=\cos \varphi +i\sin \varphi

Возведение обеих сторон в квадрат дает

ei 2 φ знак равно (соз ⁡ φ + я грех ⁡ φ) 2 {\ displaystyle e ^ {i2 \ varphi} = (\ cos \ varphi + i \ sin \ varphi) ^ {2}}

e ^ {{i2 \ varphi}} = (\ соз \ varphi + i \ sin \ varphi) ^ {{2}}

Но заменив угол на его удвоенная версия, которая дает тот же результат в левой части уравнения, дает

ei 2 φ = cos ⁡ 2 φ + i sin ⁡ 2 φ {\ disp Laystyle e ^ {i2 \ varphi} = \ cos 2 \ varphi + i \ sin 2 \ varphi}

e ^ { {i2 \ varphi}} = \ cos 2 \ varphi + i \ sin 2 \ varphi

Отсюда следует, что

(cos ⁡ φ + i sin ⁡ φ) 2 = cos ⁡ 2 φ + i sin ⁡ 2 φ {\ displaystyle (\ cos \ varphi + i \ sin \ varphi) ^ {2} = \ cos 2 \ varphi + i \ sin 2 \ varphi}

(\cos \varphi +i\sin \varphi)^{{2}}=\cos 2\varphi +i\sin 2\varphi

Расширение квадрата и упрощение в левой части уравнение дает

я (2 грех ⁡ φ соз ⁡ φ) + соз 2 ⁡ φ - грех 2 ⁡ φ = соз ⁡ 2 φ + я грех ⁡ 2 φ {\ displaystyle i (2 \ sin \ varphi \ cos \ varphi) + \ cos ^ {2} \ varphi - \ sin ^ {2} \ varphi \ = \ cos 2 \ varphi + i \ sin 2 \ varphi}

i(2\sin \varphi \cos \varphi)+\cos ^{2}\varphi -\sin ^{2}\varphi \ =\cos 2\varphi +i\sin 2\varphi

Поскольку мнимая и действительная части должны быть одинаковыми, мы остались с исходными тождествами

cos 2 ⁡ φ - sin 2 ⁡ φ = cos ⁡ 2 φ {\ displaystyle \ cos ^ {2} \ varphi - \ sin ^ {2} \ varphi \ = \ cos 2 \ varphi}

\cos ^{2}\varphi -\sin ^{2}\varphi \ =\cos 2\varphi

, а также

2 sin ⁡ φ cos ⁡ φ = sin ⁡ 2 φ {\ displaystyle 2 \ sin \ varphi \ cos \ varphi = \ sin 2 \ varphi}

2\sin \varphi \cos \varphi =\sin 2\varphi

тождества половинного угла

Два тождества, дающие альтернативные формы для cos 2θ, приводят к следующим уравнениям:

cos ⁡ θ 2 = ± 1 + cos ⁡ θ 2, {\ displaystyle \ cos {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1+ \ cos \ theta} {2}}},}

\cos {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{2}}},

sin ⁡ θ 2 = ± 1 - cos ⁡ θ 2. {\ displaystyle \ sin {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1- \ cos \ theta} {2}}}.}

\sin {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{2}}}.

Знак квадрата Корень необходимо выбрать правильно - обратите внимание, что если к θ добавляется 2π, величины внутри квадратных корней не изменяются, но левые части уравнений меняют знак. Следовательно, правильный знак зависит от значения θ.

Для функции tan уравнение выглядит следующим образом:

tan ⁡ θ 2 = ± 1 - cos ⁡ θ 1 + cos ⁡ θ. {\ displaystyle \ tan {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1- \ cos \ theta} {1+ \ cos \ theta}}}.}

{\ displaystyle \ tan {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1- \ cos \ theta} {1+ \ cos \ theta}}}.}

Затем умножение числителя и знаменателя внутри квадратного корня на (1 + cos θ) и использование тождеств Пифагора приводит к:

tan ⁡ θ 2 = sin ⁡ θ 1 + cos ⁡ θ. {\ displaystyle \ tan {\ frac {\ theta} {2}} = {\ frac {\ sin \ theta} {1+ \ cos \ theta}}.}

\tan {\frac {\theta }{2}}={\frac {\sin \theta }{1+\cos \theta }}.

Кроме того, если числитель и знаменатель умножаются по (1 - cos θ) результат:

tan ⁡ θ 2 = 1 - cos ⁡ θ sin ⁡ θ. {\ displaystyle \ tan {\ frac {\ theta} {2}} = {\ frac {1- \ cos \ theta} {\ sin \ theta}}.}

{\ displaystyle \ tan {\ frac {\ theta} {2}} = {\ frac {1- \ cos \ theta } {\ sin \ theta}}.}

Это также дает:

tan ⁡ θ 2 = csc ⁡ θ - детская кроватка ⁡ θ. {\ displaystyle \ tan {\ frac {\ theta} {2}} = \ csc \ theta - \ cot \ theta.}

\tan {\frac {\theta }{2}}=\csc \theta -\cot \theta.

Аналогичные манипуляции для функции cot дают:

cot ⁡ θ 2 = ± 1 + cos ⁡ θ 1 - cos ⁡ θ = 1 + cos ⁡ θ sin ⁡ θ = sin ⁡ θ 1 - cos ⁡ θ = csc ⁡ θ + cot ⁡ θ. {\ displaystyle \ cot {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1+ \ cos \ theta} {1- \ cos \ theta}}} = {\ frac { 1+ \ cos \ theta} {\ sin \ theta}} = {\ frac {\ sin \ theta} {1- \ cos \ theta}} = \ csc \ theta + \ cot \ theta.}

{\ displaystyle \ кроватка {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1+ \ cos \ theta} {1- \ cos \ theta}}} = {\ frac {1+ \ cos \ theta} {\ sin \ theta}} = {\ frac {\ sin \ theta} {1- \ cos \ theta}} = \ csc \ theta + \ cot \ theta.}

Разное - - тождество тройного касательного

Если $ψ + θ + ϕ = π = {\ displaystyle \ psi + \ theta + \ phi = \ pi =}$ $\psi +\theta +\phi =\pi =$ полукруг (например, $ψ {\ displaystyle \ psi}$ $\psi$ , $θ {\ displaystyle \ theta}$ $\theta$ и $ϕ {\ displaystyle \ phi}$ $\phi$ - углы треугольника),

tan ⁡ (ψ) + tan ⁡ (θ) + tan ⁡ (ϕ) = tan ⁡ (ψ) tan ⁡ (θ) tan ⁡ (ϕ). {\ Displaystyle \ tan (\ psi) + \ tan (\ theta) + \ tan (\ phi) = \ tan (\ psi) \ tan (\ theta) \ tan (\ phi).}

\ tan (\ psi) + \ tan (\ theta) + \ tan (\ phi) = \ tan (\ psi) \ tan (\ theta) \ tan (\ phi).

Доказательство:

ψ = π - θ - ϕ tan ⁡ (ψ) = tan ⁡ (π - θ - ϕ) = - tan ⁡ (θ + ϕ) = - tan ⁡ θ - tan ⁡ ϕ 1 - tan ⁡ θ tan ⁡ ϕ = tan ⁡ θ + tan ⁡ ϕ tan ⁡ θ tan ⁡ ϕ - 1 (tan ⁡ θ tan ⁡ ϕ - 1) tan ⁡ ψ = tan ⁡ θ + tan ⁡ ϕ tan ⁡ ψ tan ⁡ θ tan ⁡ ϕ - tan ⁡ ψ знак равно загар ⁡ θ + загар ⁡ ϕ загар ⁡ ψ загар ⁡ θ загар ⁡ ϕ = загар ⁡ ψ + загар ⁡ θ + загар ⁡ ϕ {\ displaystyle {\ begin {align} \ psi = \ pi - \ theta - \ phi \\\ tan (\ psi) = \ tan (\ pi - \ theta - \ phi) \\ = - \ tan (\ theta + \ phi) \\ = {\ frac {- \ tan \ theta - \ tan \ phi} {1- \ tan \ theta \ tan \ phi}} \\ = {\ frac {\ tan \ theta + \ tan \ phi} {\ tan \ theta \ tan \ phi -1}} \ \ (\ tan \ theta \ tan \ phi -1) \ tan \ psi = \ tan \ theta + \ tan \ phi \\\ tan \ psi \ tan \ theta \ tan \ phi - \ tan \ psi = \ tan \ theta + \ tan \ phi \\\ tan \ psi \ tan \ theta \ tan \ phi = \ tan \ psi + \ tan \ theta + \ tan \ phi \\\ конец {выровнено}}

{\begin{aligned}\psi =\pi -\theta -\phi \\\tan(\psi)=\tan(\pi -\theta -\phi)\\=-\tan(\theta +\phi)\\={\frac {-\tan \theta -\tan \phi }{1-\tan \theta \tan \phi }}\\={\frac {\tan \theta +\tan \phi }{\tan \theta \tan \phi -1}}\\(\tan \theta \tan \phi -1)\tan \psi =\tan \theta +\tan \phi \\\tan \psi \tan \theta \tan \phi -\tan \psi =\tan \theta +\tan \phi \\\tan \psi \tan \theta \tan \phi =\tan \psi +\tan \theta +\tan \phi \\\end{aligned}}

Разное - тождество тройного котангенса

Если $ψ + θ + ϕ = π 2 = {\ displaystyle \ psi + \ theta + \ phi = {\ tfrac {\ pi} {2}} =}$ $\psi +\theta +\phi ={\tfrac {\pi }{2}}=$ четверть круга,

детская кроватка ⁡ (ψ) + детская кроватка ⁡ (θ) + детская кроватка ⁡ (ϕ) = детская кроватка ⁡ ( ψ) детская кроватка ⁡ (θ) детская кроватка ⁡ (ϕ) {\ displaystyle \ cot (\ psi) + \ cot (\ theta) + \ cot (\ phi) = \ cot (\ psi) \ cot (\ theta) \ cot (\ phi)}

\cot(\psi)+\cot(\theta)+\cot(\phi)=\cot(\psi)\cot(\theta)\cot(\phi)

Доказательство:

Заменить каждый из $ψ {\ displaystyle \ psi}$ $\psi$ , $θ {\ displaystyle \ theta}$ $\theta$ и $ϕ {\ displaystyle \ phi}$ $\phi$ с их дополнительными углами, поэтому котангены превращаются в касательные и наоборот.

Дано

ψ + θ + ϕ = π 2 {\ displaystyle \ psi + \ theta + \ phi = {\ tfrac {\ pi} {2}}}

\psi +\theta +\phi ={\tfrac {\pi }{2}}

∴ (π 2 - ψ) + (π 2 - θ) + (π 2 - ϕ) = 3 π 2 - (ψ + θ + ϕ) = 3 π 2 - π 2 = π {\ displaystyle \, следовательно ({\ tfrac {\ pi} {2}} - \ psi) + ({\ tfrac {\ pi} {2}} - \ theta) + ({\ tfrac {\ pi} {2}} - \ phi) = {\ tfrac {3 \ pi } {2}} - (\ psi + \ theta + \ phi) = {\ tfrac {3 \ pi} {2}} - {\ tfrac {\ pi} {2}} = \ pi}

\therefore ({\tfrac {\pi }{2}}-\psi)+({\tfrac {\pi }{2}}-\theta)+({\tfrac {\pi }{2}}-\phi)={\tfrac {3\pi }{2}}-(\psi +\theta +\phi)={\tfrac {3\pi }{2}}-{\tfrac {\pi }{2}}=\pi

, поэтому результат следует из тройного касательного тождества.

Сумма с тождествами продукта

$sin ⁡ θ ± sin ⁡ ϕ = 2 sin ⁡ (θ ± ϕ 2) cos ⁡ (θ ∓ ϕ 2) {\ displaystyle \ sin \ theta \ pm \ sin \ phi = 2 \ sin \ left ({\ frac {\ theta \ pm \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta \ mp \ phi} {2}} \ right)}$ $\sin \theta \pm \sin \phi =2\sin \left({\frac {\theta \pm \phi }2}\right)\cos \left({\frac {\theta \mp \phi }2}\right)$
$соз ⁡ θ + соз ⁡ ϕ = 2 соз ⁡ (θ + ϕ 2) соз ⁡ (θ - ϕ 2) {\ displaystyle \ cos \ theta + \ cos \ phi = 2 \ cos \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta - \ phi} {2}} \ right)}$ $\cos \theta +\cos \phi =2\cos \left({\frac {\theta +\phi }2}\right)\cos \left({\frac {\theta -\phi }2}\right)$
$cos ⁡ θ - cos ⁡ ϕ = - 2 грех ⁡ (θ + ϕ 2) грех ⁡ (θ - ϕ 2) {\ displaystyle \ cos \ theta - \ cos \ phi = -2 \ sin \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ sin \ left ({\ frac {\ theta - \ phi} {2}} \ right)}$ $\cos \theta -\cos \phi =-2\sin \left({\frac {\theta +\phi }2}\right)\sin \left({\frac {\theta -\phi }2}\right)$

Доказательство синусоидальных тождеств

Сначала начнем с тождеств суммы углов:

грех ⁡ (α + β) знак равно грех ⁡ α соз ⁡ β + соз ⁡ α грех ⁡ β {\ Displaystyle \ sin (\ альфа + \ бета) = \ грех \ альфа \ соз \ бета + \ соз \ альфа \ грех \ бета}

\ sin (\ alpha + \ beta) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta

грех ⁡ (α - β) = грех ⁡ α соз ⁡ β - соз ⁡ α грех ⁡ β {\ Displaystyle \ sin (\ альфа - \ бета) = \ грех \ альфа \ соз \ бета - \ соз \ альфа \ грех \ бета}

\ sin (\ alpha - \ beta) = \ sin \ alpha \ cos \ beta - \ соз \ альфа \ грех \ бета

Сложив их вместе,

sin ⁡ (α + β) + sin ⁡ (α - β) = sin ⁡ α cos ⁡ β + cos ⁡ α sin ⁡ β + sin ⁡ α cos ⁡ β - cos ⁡ α sin ⁡ β знак равно 2 грех ⁡ α соз ⁡ β {\ Displaystyle \ грех (\ альфа + \ бета) + \ грех (\ альфа - \ бета) = \ грех \ альфа \ соз \ бета + \ соз \ альфа \ грех \ бета + \ sin \ alpha \ cos \ beta - \ cos \ alpha \ sin \ beta = 2 \ sin \ alpha \ cos \ beta}

\sin(\alpha +\beta)+\sin(\alpha -\beta)=\sin \alpha \cos \beta +\cos \alpha \sin \beta +\sin \alpha \cos \beta -\cos \alpha \sin \beta =2\sin \alpha \cos \beta

Аналогичным образом, вычитая два тождества суммы углов,

sin ⁡ (α + β) - грех ⁡ (α - β) знак равно грех ⁡ α соз ⁡ β + соз ⁡ α грех ⁡ β - грех ⁡ α соз ⁡ β + соз ⁡ α грех ⁡ β = 2 соз ⁡ α грех ⁡ β {\ Displaystyle \ sin (\ alpha + \ beta) - \ sin (\ alpha - \ beta) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta - \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta = 2 \ cos \ alpha \ sin \ beta}

\sin(\alpha +\beta)-\sin(\alpha -\beta)=\sin \alpha \cos \beta +\cos \alpha \sin \beta -\sin \alpha \cos \beta +\cos \alpha \sin \beta =2\cos \alpha \sin \beta

Пусть $α + β = θ {\ displaystyle \ alpha + \ beta = \ theta}$ $\alpha +\beta =\theta$ и $α - β знак равно ϕ {\ Displaystyle \ альфа - \ бета = \ phi}$ $\alpha -\beta =\phi$ ,

∴ α = θ + ϕ 2 {\ displaystyle \, следовательно, \ alpha = {\ frac {\ theta + \ phi} {2}}}

\ поэтому \ alpha = {\ frac {\ theta + \ phi} 2}

β = θ - ϕ 2 {\ displaystyle \ beta = {\ frac {\ theta - \ phi} {2}}}

\beta ={\frac {\theta -\phi }2}

Заменить $θ {\ displaystyle \ theta}$ $\theta$ и $ϕ {\ displaystyle \ phi}$ $\phi$

sin ⁡ θ + sin ⁡ ϕ = 2 sin ⁡ (θ + ϕ 2) соз ⁡ (θ - ϕ 2) {\ displaystyle \ sin \ theta + \ sin \ phi = 2 \ sin \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ cos \ left ({ \ frac {\ theta - \ phi} {2}} \ right)}

\ sin \ theta + \ sin \ phi = 2 \ sin \ left ({\ frac {\ theta + \ phi} 2} \ right) \ cos \ left ({\ frac {\ theta - \ phi} 2} \ right)

sin ⁡ θ - sin ⁡ ϕ = 2 cos ⁡ (θ + ϕ 2) sin ⁡ (θ - ϕ 2) = 2 sin ⁡ ( θ - ϕ 2) соз ⁡ (θ + ϕ 2) {\ displaystyle \ sin \ theta - \ sin \ phi = 2 \ cos \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ sin \ left ({\ frac {\ theta - \ phi} {2}} \ right) = 2 \ sin \ left ({\ frac {\ theta - \ phi} {2}} \ right) \ cos \ left ( {\ frac {\ theta + \ phi} {2}} \ right)}

\sin \theta -\sin \phi =2\cos \left({\frac {\theta +\phi }2}\right)\sin \left({\frac {\theta -\phi }2}\right)=2\sin \left({\frac {\theta -\phi }2}\right)\cos \left({\frac {\theta +\phi }2}\right)

Следовательно,

sin ⁡ θ ± sin ⁡ ϕ = 2 sin ⁡ (θ ± ϕ 2) cos ⁡ (θ ∓ ϕ 2) {\ displaystyle \ sin \ theta \ pm \ sin \ phi = 2 \ sin \ left ({\ frac {\ theta \ pm \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta \ mp \ phi} {2}} \ right)}

\sin \theta \pm \sin \phi =2\sin \left({\frac {\theta \pm \phi }2}\right)\cos \left({\frac {\theta \mp \phi }2}\right)

Доказательство косинусных тождеств

Аналогично косинусу, начните с тождеств суммы углов:

cos ⁡ (α + β) = cos ⁡ α соз ⁡ β - грех ⁡ α грех ⁡ β {\ Displaystyle \ соз ( \ alpha + \ beta) = \ cos \ alpha \ cos \ beta \ - \ sin \ alpha \ sin \ beta}

\cos(\alpha +\beta)=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta

cos ⁡ (α - β) = cos ⁡ α cos ⁡ β + sin ⁡ α sin ⁡ β {\ Displaystyle \ соз (\ альфа - \ бета) = \ соз \ альфа \ соз \ бета + \ грех \ альфа \ грех \ бета}

\cos(\alpha -\beta)=\cos \alpha \cos \beta +\sin \alpha \sin \beta

Опять же, добавляя и вычитая

соз ⁡ (α + β) + соз ⁡ (α - β) знак равно соз ⁡ α соз ⁡ β - грех ⁡ α грех ⁡ β + соз ⁡ α соз ⁡ β + грех ⁡ α грех ⁡ β = 2 соз ⁡ α соз ⁡ β {\ Displaystyle \ соз ( \ alpha + \ beta) + \ cos (\ alpha - \ beta) = \ cos \ alpha \ cos \ beta \ - \ sin \ alpha \ sin \ beta + \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta = 2 \ cos \ alpha \ cos \ beta}

{\ Displaystyle \ соз (\ альфа + \ бета) + \ соз (\ альфа - \ бета) = \ соз \ альфа \ соз \ бета \ - \ грех \ альфа \ грех \ бета + \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta = 2 \ cos \ alpha \ cos \ beta}

cos ⁡ (α + β) - cos ⁡ (α - β) = cos ⁡ α cos ⁡ β - sin ⁡ α sin ⁡ β - cos ⁡ α соз ⁡ β - грех ⁡ α грех ⁡ β знак равно - 2 грех ⁡ α грех ⁡ β {\ Displaystyle \ соз (\ альфа + \ бета) - \ соз (\ альфа - \ бета) = \ соз \ альфа \ соз \ бета \ - \ sin \ alpha \ sin \ beta - \ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta = -2 \ sin \ alpha \ sin \ beta}

\cos (\alpha + \beta) - \cos (\alpha - \beta) = \cos \alpha \cos \beta\ - \sin \alpha \sin \beta - \cos \alpha \cos \beta - \sin \alpha \sin \beta = -2 \sin \alpha \sin \beta

Заменить $θ {\ displaystyle \ theta}$ $\theta$ и $ϕ {\ displaystyle \ phi}$ $\phi$ как и раньше,

cos ⁡ θ + соз ⁡ ϕ знак равно 2 соз ⁡ (θ + ϕ 2) соз ⁡ (θ - ϕ 2) {\ displaystyle \ cos \ theta + \ cos \ phi = 2 \ cos \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta - \ phi} {2}} \ right)}

\cos \theta +\cos \phi =2\cos \left({\frac {\theta +\phi }2}\right)\cos \left({\frac {\theta -\phi }2}\right)

cos ⁡ θ - cos ⁡ ϕ = - 2 sin ⁡ (θ + ϕ 2) грех ⁡ (θ - ϕ 2) {\ displaystyle \ cos \ theta - \ cos \ phi = -2 \ sin \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ sin \ left ({\ frac {\ theta - \ phi} {2}} \ right)}

\cos \theta -\cos \phi =-2\sin \left({\frac {\theta +\phi }2}\right)\sin \left({\frac {\theta -\phi }2}\right)

Неравенства

Иллюстрация неравенств синуса и касательной.

На рисунке справа показан сектор окружности с радиусом 1. Сектор равен θ / (2π) всей окружности, поэтому его площадь равна θ / 2. Здесь мы предполагаем, что θ < π/2.

OA = OD = 1 {\ displaystyle OA = OD = 1}

OA=OD=1

AB = sin ⁡ θ {\ displaystyle AB = \ sin \ theta}

AB=\sin \theta

CD = tan ⁡ θ {\ displaystyle CD = \ tan \ theta}

CD=\tan \theta

Площадь треугольника OAD равна AB / 2 или sin (θ) / 2. Площадь треугольника OCD равна CD / 2 или tan (θ) / 2.

Поскольку треугольник OAD полностью лежит внутри сектора, который, в свою очередь, полностью лежит внутри треугольника OCD, мы имеем

sin ⁡ θ < θ < tan ⁡ θ. {\displaystyle \sin \theta <\theta <\tan \theta.}

\sin \theta <\theta <\tan \theta.

Этот геометрический аргумент основан на определениях длины дуги и area, которые действуют как предположения, поэтому это скорее условие, налагаемое при построении тригонометрических функций, чем доказуемое свойство. Для синусоидальной функции мы можем обрабатывать другие значения. Если θ>π / 2, то θ>1. Но sin θ ≤ 1 (из-за тождества Пифагора), поэтому sin θ < θ. So we have

sin ⁡ θ θ < 1 i f 0 < θ. {\displaystyle {\frac {\sin \theta }{\theta }}<1\ \ \ \mathrm {if} \ \ \ 0<\theta.}

{\frac {\sin \theta }{\theta }}<1\ \ \ \mathrm {if} \ \ \ 0<\theta.

Для отрицательных значений θ мы имеем, симметрично функции синуса

sin ⁡ θ θ = sin ⁡ (- θ) - θ < 1. {\displaystyle {\frac {\sin \theta }{\theta }}={\frac {\sin(-\theta)}{-\theta }}<1.}

{\frac {\sin \theta }{\theta }}={\frac {\sin(-\theta)}{-\theta }}<1.

Следовательно,

sin ⁡ θ θ < 1 if θ ≠ 0, {\displaystyle {\frac {\sin \theta }{\theta }}<1\quad {\text{if }}\quad \theta \neq 0,}

{\frac {\sin \theta }{\theta }}<1\quad {\text{if }}\quad \theta \neq 0,

tan ⁡ θ θ>1, если 0 < θ < π 2. {\displaystyle {\frac {\tan \theta }{\theta }}>1 \ quad {\ text {if}} \ quad 0 <\theta <{\frac {\pi }{2}}.}

{\frac {\tan \theta }{\theta }}>1 \ quad {\ text {if}} \ quad 0 <\theta <{\frac {\pi }{2}}.

Идентичности, связанные с исчислением

Предварительные сведения

lim θ → 0 sin ⁡ θ = 0 {\ displaystyle \ lim _ {\ тета \ к 0} {\ грех \ тета} = 0}

\lim _{\theta \to 0}{\sin \theta }=0

lim θ → 0 соз ⁡ θ = 1 {\ displaystyle \ lim _ {\ theta \ to 0} {\ cos \ theta} = 1}

\lim _{\theta \to 0}{\cos \theta }=1

Тождество синуса и углового отношения

lim θ → 0 грех ⁡ θ θ = 1 {\ displaystyle \ lim _ {\ theta \ to 0} {\ frac {\ sin \ theta} {\ theta}} = 1}

\lim _{{\theta \to 0}}{{\frac {\sin \theta }{\theta }}}=1

Другими словами, функция синус дифференцируема в 0, а ее производная равна 1.

Доказательство: из предыдущих неравенств для малых angles

sin ⁡ θ < θ < tan ⁡ θ {\displaystyle \sin \theta <\theta <\tan \theta }

{\ displaystyle \ sin \ theta <\ theta <\ tan \ theta}

Следовательно,

sin ⁡ θ θ < 1 < tan ⁡ θ θ {\displaystyle {\frac {\sin \theta }{\theta }}<1<{\frac {\tan \theta }{\theta }}}

{\frac {\sin \theta }{\theta }}<1<{\frac {\tan \theta }{\theta }}

Рассмотрим правое неравенство. Поскольку

загар ⁡ θ = грех ⁡ θ соз ⁡ θ {\ displaystyle \ tan \ theta = {\ frac {\ sin \ theta} {\ cos \ theta}}}

\tan \theta ={\frac {\sin \theta }{\cos \theta }}

∴ 1 < sin ⁡ θ θ cos ⁡ θ {\displaystyle \therefore 1<{\frac {\sin \theta }{\theta \cos \theta }}}

\therefore 1<{\frac {\sin \theta }{\theta \cos \theta }}

Умножить на $cos ⁡ θ {\ displaystyle \ cos \ theta}$ $\cos \theta$

cos ⁡ θ < sin ⁡ θ θ {\displaystyle \cos \theta <{\frac {\sin \theta }{\theta }}}

\ cos \ theta <{\ frac {\ sin \ theta} {\ theta}}

В сочетании с левым неравенством:

cos ⁡ θ < sin ⁡ θ θ < 1 {\displaystyle \cos \theta <{\frac {\sin \theta }{\theta }}<1}

\cos \theta <{\frac {\sin \theta }{\theta }}<1

Принимая $cos ⁡ θ {\ displaystyle \ соз \ theta}$ $\cos \theta$ до предела, как $θ → 0 {\ displaystyle \ theta \ to 0}$ $\ theta \ to 0$

lim θ → 0 cos ⁡ θ = 1 {\ displaystyle \ lim _ {\ theta \ to 0} {\ cos \ theta} = 1}

\lim _{\theta \to 0}{\cos \theta }=1

Следовательно,

lim θ → 0 sin ⁡ θ θ = 1 {\ displaystyle \ lim _ {\ theta \ to 0} {\ frac {\ sin \ theta} {\ theta}} = 1}

\lim _{{\theta \to 0}}{{\frac {\sin \theta }{\theta }}}=1

Косинус и тождество углового отношения

lim θ → 0 1 - cos ⁡ θ θ = 0 {\ displaystyle \ lim _ {\ theta \ to 0} {\ frac {1- \ cos \ theta} {\ theta}} = 0}

\lim _{{\theta \to 0}}{\frac {1-\cos \theta }{\theta }}=0

Доказательство:

1 - cos ⁡ θ θ = 1 - cos 2 ⁡ θ θ (1 + cos ⁡ θ) = sin 2 ⁡ θ θ (1 + соз ⁡ θ) = (грех ⁡ θ θ) × грех ⁡ θ × (1 1 + соз ⁡ θ) {\ displaystyle {\ begin {align} {\ frac {1- \ cos \ theta} { \ theta}} = {\ frac {1- \ cos ^ {2} \ theta} {\ theta (1+ \ cos \ theta)}} \\ = {\ frac {\ sin ^ {2} \ theta } {\ t heta (1+ \ cos \ theta)}} \\ = \ left ({\ frac {\ sin \ theta} {\ theta}} \ right) \ times \ sin \ theta \ times \ left ({\ frac { 1} {1+ \ cos \ theta}} \ right) \\\ end {align}}}

{\begin{aligned}{\frac {1-\cos \theta }{\theta }}={\frac {1-\cos ^{2}\theta }{\theta (1+\cos \theta)}}\\={\frac {\sin ^{2}\theta }{\theta (1+\cos \theta)}}\\=\left({\frac {\sin \theta }{\theta }}\right)\times \sin \theta \times \left({\frac {1}{1+\cos \theta }}\right)\\\end{aligned}}

Пределы этих трех величин равны 1, 0 и 1/2, поэтому результирующий предел равен нулю.

Косинус и квадрат углового отношения идентичны

lim θ → 0 1 - cos ⁡ θ θ 2 = 1 2 {\ displaystyle \ lim _ {\ theta \ to 0} {\ frac {1- \ cos \ theta} {\ theta ^ {2}}} = {\ frac {1} {2}}}

\ lim _ {{\ theta \ to 0}} {\ frac {1- \ cos \ theta} {\ theta ^ {2}}} = {\ frac {1} {2} }

Доказательство:

Как и в предыдущем доказательстве,

1 - cos ⁡ θ θ 2 = грех ⁡ θ θ × sin ⁡ θ θ × 1 1 + соз ⁡ θ. {\ displaystyle {\ frac {1- \ cos \ theta} {\ theta ^ {2}}} = {\ frac {\ sin \ theta} {\ theta}} \ times {\ frac {\ sin \ theta} { \ theta}} \ times {\ frac {1} {1+ \ cos \ theta}}.}

{\ displaystyle {\ frac {1- \ cos \ theta} {\ theta ^ {2}}} = { \ frac {\ sin \ theta} {\ theta}} \ times {\ frac {\sin \theta }{\theta }}\times {\frac {1}{1+\cos \theta }}.}

Пределы этих трех величин равны 1, 1 и 1/2, поэтому конечный предел равен 1/2.

Доказательство сочетания тригонометрических и обратных тригонометрических функций

Все эти функции вытекают из тригонометрического тождества Пифагора. Мы можем доказать, например, функцию

sin ⁡ [arctan ⁡ (x)] = x 1 + x 2 {\ displaystyle \ sin [\ arctan (x)] = {\ frac {x} {\ sqrt {1+ x ^ {2}}}}}

\sin[\arctan(x)]=\frac{x}{\sqrt{1+x^2}}

Доказательство:

Начнем с

sin 2 ⁡ θ + cos 2 ⁡ θ = 1 {\ displaystyle \ sin ^ {2} \ theta + \ cos ^ {2} \ theta = 1}

\sin ^{2}\theta +\cos ^{2}\theta =1

Затем мы разделим это уравнение на $cos 2 ⁡ θ {\ displaystyle \ cos ^ {2} \ theta}$ $\cos ^{2}\theta$

cos 2 ⁡ θ = 1 tan 2 ⁡ θ + 1 {\ displaystyle \ cos ^ {2} \ theta = {\ frac {1} {\ tan ^ {2} \ theta +1}}}

\cos ^{2}\theta ={\frac {1}{\tan ^{2}\theta +1}}

Затем используйте замену $θ = arctan ⁡ ( x) {\ displaystyle \ theta = \ arctan (x)}$ $\theta =\arctan(x)$ , также используйте тригонометрическое тождество Пифагора:

1 - sin 2 ⁡ [arctan ⁡ (x)] = 1 tan 2 ⁡ [arctan ⁡ (x)] + 1 {\ displaystyle 1- \ sin ^ {2} [\ arctan (x)] = {\ frac {1} {\ tan ^ {2} [\ arctan (x)] + 1}} }

1- \ sin ^ {2} [\ arctan (x) ] = {\ гидроразрыва {1} {\ tan ^ {2} [\ arctan (x)] + 1}}

Затем мы используем тождество $tan ⁡ [arctan ⁡ (x)] ≡ x {\ displaystyle \ tan [\ arctan (x)] \ Equiv x}$ $\tan[\arctan(x)]\equiv x$

sin ⁡ [arctan ⁡ (x) ] = xx 2 + 1 {\ displaystyle \ sin [\ arctan (x)] = {\ frac {x} {\ sqrt {x ^ {2} +1}}}}

\sin[\arctan(x)]={\frac {x}{{\sqrt {x^{2}+1}}}}

См. также

Примечания

Ссылки