Хэмминг (7,4)

Хэмминг (7,4) -Код
Назван в честь	Ричарда В. Хэмминга
Классификация
Тип	Линейный код блока
Длина блока	7
Длина сообщения	4
Скорость	4/7 ~ 0,571
Расстояние	3
Размер алфавита	2
Обозначение	[ 7,4,3] 2 -код
Свойства
совершенный код
v t

Графическое изображение 4 битов данных от d 1 до d 4 и 3 бита четности p 1 до p 3 и какие биты четности применяются к каким битам данных

В теории кодирования, Хэмминга (7, 4) - это код линейного исправления ошибок, который кодирует четыре бита данных в семь битов путем добавления трех битов четности. Это член более крупного семейства кодов Хэмминга, но термин код Хэмминга часто относится к этому конкретному коду, который Ричард У. Хэмминг ввел в 1950 году. В то время Хэмминг работал в Bell Telephone Laboratories и был разочарован подверженным ошибкам считывателем перфокарт , поэтому он начал работать над кодами исправления ошибок.

Код Хэмминга добавляет три дополнительных контрольных бита на каждые четыре бита данных сообщения. Алгоритм Хэмминга (7,4) может исправить любую однобитовую ошибку или обнаружить все однобитовые и двухбитовые ошибки. Другими словами, минимальное расстояние Хэмминга между любыми двумя правильными кодовыми словами равно 3, и принятые слова могут быть правильно декодированы, если они находятся на расстоянии не более одного от кодового слова, которое было передано отправителем. Это означает, что для ситуаций среды передачи, в которых пакетных ошибок не возникает, эффективен код Хэмминга (7,4) (поскольку среда должна быть чрезвычайно шумной для переключения двух из семи битов).

В квантовой информации код Хэмминга (7,4) используется в качестве основы для кода Стейна, типа кода CSS используется для квантовой коррекции ошибок.

• 1 Цель
• 2 Матрицы Хэмминга
• 3 Канальное кодирование
• 4 Проверка четности
• 5 Исправление ошибок
• 6 Декодирование
• 7 Множественные битовые ошибки
• 8 Все кодовые слова
• 9 E 7 решетка
• 10 Ссылки
• 11 Внешние ссылки

Целью кодов Хэмминга является для создания набора битов четности, которые перекрываются, так что однобитовая ошибка в бите данных или бите четности может быть обнаружена и исправлена. Хотя может быть создано несколько перекрытий, общий метод представлен в кодах Хэмминга.

Бит №	1	2	3	4	5	6	7
Переданный бит	$p\; 1\; \{\backslash \; displaystyle\; p\_\; \{1\}\}$	$p\; 2\; \{\backslash \; displaystyle\; p\_\; \{2\}\}$	$d\; 1\; \{\backslash \; displaystyle\; d\_\; \{1\}\}$	$p\; 3\; \{\backslash \; displaystyle\; p\_\; \{3\}\}$	$d\; 2\; \{\backslash \; displaystyle\; d\_\; \{2\}\}$	$d\; 3\; \{\backslash \; displaystyle\; d\_\; \{3\}\}$	$d\; 4\; \{\backslash \; displaystyle\; d\_\; \{4\}\}$
$p\; 1\; \{\backslash \; displaystyle\; p\_\; \{1\}\}$	Да	Нет	Да	Нет	Да	Нет	Да
$p\; 2\; \{\backslash \; displaystyle\; p\_\; \{2\}\}$	Нет	Да	Да	Нет	Нет	Да	Да
$p\; 3\; \{\backslash \; displaystyle\; p\_\; \{3\}\}$	Нет	Нет	Нет	Да	Да	Да	Да

Это Таблица описывает, какие биты четности покрывают переданные биты в закодированном слове. Например, p 2 обеспечивает четность для битов 2, 3, 6 и 7. Он также детализирует, какой переданный бит покрывается каким битом четности при чтении столбца. Например, d 1 покрывается p 1 и p 2, но не p 3. Эта таблица будет иметь поразительное сходство с таблицей. матрица проверки на четность (H ) в следующем разделе.

Кроме того, если столбцы четности в приведенной выше таблице были удалены

	$d\; 1\; \{\backslash \; displaystyle\; d\_\; \{1\}\}$	$d\; 2\; \{\backslash \; displaystyle\; d\_\; \{2\}\}$	$d\; 3\; \{\; \backslash \; displaystyle\; d\_\; \{3\}\}$	$d\; 4\; \{\backslash \; displaystyle\; d\_\; \{4\}\}$
$p\; 1\; \{\backslash \; displaystyle\; p\_\; \{1\}\}$	Да	Да	Нет	Да
$p\; 2\; \{\backslash \; displaystyle\; p\_\; \{2\}\}$	Да	Нет	Да	Да
$p\; 3\; \{\backslash \; displaystyle\; p\_\; \{3\}\}$	Нет	Да	Да	Да

, тогда сходство со строками 1, 2 и 4 кода образующая матрица (G ) ниже также будет очевидна.

Таким образом, при правильном выборе покрытия битов четности все ошибки с расстоянием Хэмминга, равным 1, могут быть обнаружены и исправлены, что и является целью использования кода Хэмминга.

Коды Хэмминга могут быть вычислены в терминах линейной алгебры через матрицы, потому что коды Хэмминга являются линейными кодами. Для кодов Хэмминга могут быть определены две матрицы Хэмминга : порождающая матрица кода Gи матрица проверки на четность H:

$GT:\; =\; (1\; 1\; 0\; 1\; 1\; 0\; 1\; 1\; 1\; 0\; 0\; 0\; 0\; 1\; 1\; 1\; 0\; 1\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 1),\; H:\; =\; (1\; 0\; 1\; 0\; 1\; 0\; 1\; 0\; 1\; 1\; 0\; 0\; 1\; 1\; 0\; 0\; 0\; 1\; 1\; 1\; 1).\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{G\; ^\; \{T\}\}:\; =\; \{\backslash \; begin\; \{pmatrix\}\; 1\; 1\; 0\; 1\; \backslash \backslash \; 1\; 0\; 1\; 1\; \backslash \backslash \; 1\; 0\; 0\; 0\; \backslash \backslash \; 0\; 1\; 1\; 1\; \backslash \backslash \; 0\; 1\; 0\; 0\; \backslash \backslash \; 0\; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 0\; 1\; \backslash \backslash \}\; end\; \{pqumatrix\}\; \backslash \; mathbf\; \{H\}:\; =\; \{\backslash \; begin\; \{pmatrix\}\; 1\; 0\; 1\; 0\; 1\; 0\; 1\; \backslash \backslash \; 0\; 1\; 1\; 0\; 0\; 1\; 1\; 1\; \backslash \backslash \; 0\; 0\; 0\; 1\; 1\; 1\; 1\; \backslash \backslash \backslash \; end\; \{pmatrix\}\}.\}$

Разрядность строк и биты четности

Как упоминалось выше,, 2 и 4 из G должны выглядеть знакомо, поскольку они отображают биты данных в свои биты четности:

• p1охватывает d 1, d 2, d 4
• p2охватывает d 1, d 3, d 4
• p3охватывает d 2, d 3, d 4

оставшиеся строки (3, 5, 6, 7) отображают данные в их позицию в закодированной форме, и в этой строке только 1, поэтому это идентичная копия. Фактически, эти четыре строки являются линейно независимыми и образуют единичную матрицу (по замыслу, а не совпадение).

Также, как упоминалось выше, три строки H должны быть знакомы. Эти строки используются для вычисления вектора синдрома на принимающей стороне, и если вектор синдрома является нулевым вектором (все нули), то полученное слово не содержит ошибок; если не ноль, то значение указывает, какой бит был перевернут.

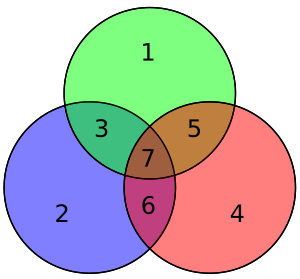
Четыре бита данных, собранные как вектор p, предварительно умножаются на G (т. Е. Gp ) и берутся по модулю 2, чтобы получить передаваемое закодированное значение. Исходные 4 бита данных преобразуются в семь битов (отсюда и название «Хэмминга (7,4)») с добавлением трех битов четности для обеспечения четности с использованием вышеуказанных покрытий битов данных. В первой таблице выше показано отображение между каждым битом данных и битом четности в его конечную битовую позицию (с 1 по 7), но это также может быть представлено на диаграмме Венна. На первой диаграмме в этой статье показаны три круга (по одному для каждого бита четности), в которые включены биты данных, которые покрывает каждый бит четности. Вторая диаграмма (показанная справа) идентична, но вместо этого отмечены позиции битов.

В оставшейся части этого раздела следующие 4 бита (показаны как вектор-столбец) будут использоваться в качестве рабочего примера:

$p\; =\; (d\; 1\; d\; 2\; d\; 3\; d\; 4)\; =\; (1\; 0\; 1\; 1)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; d\_\; \{1\}\; \backslash \backslash \; d\_\; \{2\}\; \backslash \backslash \; d\_\; \{3\}\; \backslash \backslash \; d\_\; \{4\}\; \backslash \backslash \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\}$

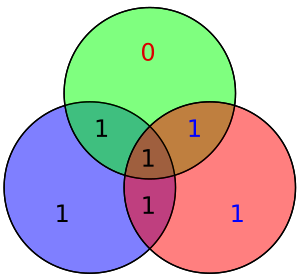
Отображение в примере x . Четность красных, зеленых и синих кругов четная.

Предположим, мы хотим передать эти данные (1011) по шумному каналу связи. В частности, двоичный симметричный канал означает, что искажение ошибок не способствует ни нулю, ни единице (он симметричен по возникновению ошибок). Кроме того, предполагается, что все исходные векторы равновероятны. Возьмем произведение G и p с элементами по модулю 2, чтобы определить переданное кодовое слово x:

$x\; =\; G\; p\; =\; (1\; 1\; 0\; 1\; 1\; 0\; 1\; 1\; 1\; 0\; 0\; 0\; 0\; 1\; 1\; 1\; 0\; 1\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 1)\; (1\; 0\; 1\; 1)\; =\; (2\; 3\; 1\; 2\; 0\; 1\; 1)\; =\; (0\; 1\; 1\; 0\; 0\; 1\; 1)\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{x\}\; =\; \backslash \; mathbf\; \{G\}\; \backslash \; mathbf\; \{p\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 1\; 1\; 0\; 1\; \backslash \backslash \; 1\; 0\; 1\; 1\; \backslash \backslash \; 1\; 0\; 0\; 0\; \backslash \backslash \; 0\; 1\; 1\; 1\; \backslash \backslash \; 0\; 1\; 0\; 0\; \backslash \backslash \; 0\; 0\; 1\; 1\; 0\; \backslash \backslash \; 0\; 0\; 0\; 1\; \backslash \backslash \; \}\backslash \}\; end\; \{p\; begin\; \{pmatrix\}\; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 2\; \backslash \backslash \; 3\; \backslash \backslash \; 1\; \backslash \backslash \; 2\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\; \}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\}$

Это означает, что 0110011будет передается вместо передачи 1011.

Программисты, озабоченные умножением, должны заметить, что каждая строка результата является младшим значащим битом Счетчика популяции установленных битов, полученных в результате того, что строка и столбец Побитовое И, а не умножение.

На соседней диаграмме семь бит кодированного слова вставлены в свои соответствующие места; при осмотре видно, что четность красного, зеленого и синего кругов четная:

• красный круг имеет две единицы
• зеленый круг имеет две единицы
• синий круг имеет четыре единицы

Вскоре будет показано, что если во время передачи бит перевернут, то четность двух или всех трех кругов будет неправильной, и ошибочный бит может быть определен (даже если один из битов четности), зная, что четность всех трех этих кругов должна быть четной.

Если во время передачи ошибок не возникает, то полученное кодовое слово r идентично переданному кодовому слову x:

$r\; =\; x\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\; r\}\; =\; \backslash \; mathbf\; \{x\}\}$

Получатель умножает H и r, чтобы получить вектор синдрома z, который указывает, произошла ли ошибка, и если да, то для какого бита кодового слова. Выполнение этого умножения (опять же, записи по модулю 2):

$z\; =\; H\; r\; =\; (1\; 0\; 1\; 0\; 1\; 0\; 1\; 0\; 1\; 1\; 0\; 0\; 1\; 1\; 0\; 0\; 0\; 1\; 1\; 1\; 1)\; (0\; 1\; 1\; 0\; 0\; 1\; 1)\; =\; (2\; 4\; 2)\; =\; (0\; 0\; 0)\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{z\}\; =\; \backslash \; mathbf\; \{H\}\; \backslash \; mathbf\; \{r\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 1\; 0\; 1\; 0\; 1\; 0\; 1\; \backslash \backslash \; 0\; 1\; 1\; 0\; 0\; 1\; 1\; \backslash \backslash \; 0\; \backslash \; 0\; 1\; 1\; end\; 1\; 1\; \backslash \; \{pmatrix\}\}\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 2\; \backslash \backslash \; 4\; \backslash \backslash \; 2\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\}$

Поскольку синдром z является нулевым вектором, приемник может сделать вывод, что ошибки не произошло. Этот вывод основан на наблюдении, что когда вектор данных умножается на G, смена базиса происходит в векторном подпространстве, которое является ядром H . Пока во время передачи ничего не происходит, r будет оставаться в ядре H, и умножение даст нулевой вектор.

В противном случае предположим, что произошла ошибка одного бита. Математически мы можем написать

$r\; =\; x\; +\; ei\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{r\}\; =\; \backslash \; mathbf\; \{x\}\; +\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\}$

по модулю 2, где ei- это $ith\; \{\backslash \; displaystyle\; i\_\; \{th\}\}$единичный вектор, то есть нулевой вектор с 1 в $i\; \{\backslash \; displaystyle\; i\; ^\; \{th\}\}$, считая от 1.

$e\; 2\; =\; (0\; 1\; 0\; 0\; 0\; 0\; 0)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{2\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\}$

Таким образом, приведенное выше выражение означает одну битовую ошибку в $i\; \{\backslash \; displaystyle\; i\; ^\; \{th\}\}$месте.

Теперь, если мы умножим этот вектор на H:

$H\; r\; =\; H\; (x\; +\; ei)\; =\; H\; x\; +\; H\; ei\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{Hr\}\; =\; \backslash \; mathbf\; \{H\}\; \backslash \; left\; (\backslash \; mathbf\; \{x\}\; +\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\; \backslash \; right)\; =\; \backslash \; mathbf\; \{Hx\}\; +\; \backslash \; mathbf\; \{He\}\; \_\; \{i\}\}$

Поскольку x - переданные данные, это безошибочно, и в результате произведение H и x равно нулю. Таким образом,

$H\; x\; +\; H\; ei\; =\; 0\; +\; H\; ei\; =\; H\; ei\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{Hx\}\; +\; \backslash \; mathbf\; \{He\}\; \_\; \{i\}\; =\; \backslash \; mathbf\; \{0\}\; +\; \backslash \; mathbf\; \{He\}\; \_\; \{i\; \}\; =\; \backslash \; mathbf\; \{He\}\; \_\; \{i\}\}$

Теперь произведение H со стандартным базисом $i\; \{\backslash \; displaystyle\; i\; ^\; \{th\}\}$vector выбирает этот столбец H, мы знаем, что ошибка возникает в том месте, где встречается этот столбец H .

Например, предположим, что мы ввели битовую ошибку в бит №5

$r\; =\; x\; +\; e\; 5\; =\; (0\; 1\; 1\; 0\; 0\; 1\; 1)\; +\; (0\; 0\; 0\; 0\; 1\; 0\; 0)\; =\; (0\; 1\; 1\; 0\; 1\; 1\; 1)\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{r\}\; =\; \backslash \; mathbf\; \{x\}\; +\; \backslash \; mathbf\; \{e\}\; \_\; \{5\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\; +\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\}$

Битовая ошибка в бите 5 приводит к плохой четности в красных и зеленых кругах

На диаграмме справа показаны битовая ошибка (показана синим текстом) и созданная плохая четность (показана красным текстом) в красном и зеленом кругах. Битовую ошибку можно обнаружить, вычислив четность красного, зеленого и синего кружков. Если обнаружена плохая четность, то бит данных, который перекрывает только круги плохой четности, является битом с ошибкой. В приведенном выше примере красный и зеленый кружки имеют плохую четность, поэтому бит, соответствующий пересечению красного и зеленого, но не синего, указывает на бит с ошибкой.

Теперь

$z\; =\; H\; r\; =\; (1\; 0\; 1\; 0\; 1\; 0\; 1\; 0\; 1\; 1\; 0\; 0\; 1\; 1\; 0\; 0\; 0\; 1\; 1\; 1\; 1)\; (0\; 1\; 1\; 0\; 1\; 1\; 1)\; =\; (\; 3\; 4\; 3)\; =\; (1\; 0\; 1)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{z\}\; =\; \backslash \; mathbf\; \{Hr\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 1\; 0\; 1\; 0\; 1\; 0\; 1\; \backslash \backslash \; 0\; 1\; 1\; 0\; 0\; 1\; 1\; \backslash \backslash \; 0\; 0\; 0\; 0\; 1\; 1\; 1\; 1\; \backslash \backslash \backslash \; end\; \{begin\; \{pmatrix\}\}\; \{\; pmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 3\; \backslash \backslash \; 4\; \backslash \backslash \; 3\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\}$

, что соответствует пятому столбцу H . Кроме того, использованный общий алгоритм (см. код Хэмминга # Общий алгоритм ) был преднамеренным в своей конструкции, так что синдром 101 соответствует двоичному значению 5, которое указывает, что пятый бит был поврежден. Таким образом, в бите 5 обнаружена ошибка, и ее можно исправить (просто переверните или отмените ее значение):

$r\; исправлено\; =\; (0\; 1\; 1\; 0\; 1\; ¯\; 1\; 1)\; =\; (0\; 1\; 1\; 0\; 0\; 1\; 1)\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{r\}\; \_\; \{\backslash \; text\; \{исправлено\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \backslash \; 0\; \backslash \backslash \; \{\backslash \; overline\; \{1\}\}\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\}$

Это исправленное полученное значение действительно теперь соответствует переданное значение x сверху.

После того, как полученный вектор был определен как свободный от ошибок или исправлен, если произошла ошибка (при условии, что возможны только нулевые или однобитовые ошибки), тогда полученные данные необходимо декодировать обратно в исходные четыре бита.

Сначала определите матрицу R:

$R\; =\; (0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 1)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; 1\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; 0\; 0\; 1\; \backslash \backslash \backslash \; end\; \{pmatrix\}\}\}$

<40867>, полученное значение равно <40867>212>. Используя приведенный выше пример выполнения

$pr\; =\; (0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 1)\; (0\; 1\; 1\; 0\; 0\; 1\; 1)\; =\; (1\; 0\; 1\; 1)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\_\; \{r\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; 1\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 1\; \backslash \backslash \}\; end\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 1\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\}$

В битах 4 и 5 появляются битовые ошибки (показаны синим текстом) с плохой четностью только в зеленом кружке (показанном красным текстом)

Нетрудно показать, что только одиночные битовые ошибки могут быть исправлены с помощью этой схемы. В качестве альтернативы, коды Хэмминга могут использоваться для обнаружения одиночных и двойных битовых ошибок, просто отмечая, что произведение H не равно нулю всякий раз, когда возникают ошибки. На соседней диаграмме биты 4 и 5 были перевернуты. Это дает только один кружок (зеленый) с недопустимой четностью, но ошибки не подлежат исправлению.

Однако код Хэмминга (7,4) и аналогичные коды Хэмминга не могут различать однобитовые ошибки и двухбитовые ошибки. То есть двухбитовые ошибки появляются так же, как однобитовые ошибки. Если исправление ошибок выполняется для двухбитовой ошибки, результат будет неверным.

Точно так же коды Хэмминга не могут обнаружить или исправить произвольную трехбитовую ошибку; Рассмотрим диаграмму: если бы бит в зеленом кружке (окрашенный в красный цвет) был равен 1, проверка четности вернула бы нулевой вектор, указывая, что в кодовом слове нет ошибки.

Поскольку у источника всего 4 бита, то есть только 16 возможных передаваемых слов. Включено восьмибитовое значение, если используется дополнительный бит четности (см. код Хэмминга (7,4) с дополнительным битом четности ). (Биты данных показаны синим цветом; биты четности показаны красным; бит дополнительной четности показан желтым.)

Данные. $(d\; 1,\; d\; 2,\; d\; 3,\; d\; 4)\; \{\backslash \; displaystyle\; (\{\backslash \; color\; \{blue\}\; d\_\; \{1\}\},\; \{\backslash \; color\; \{blue\}\; d\_\; \{2\}\},\; \{\backslash \; color\; \{blue\}\; d\_\; \{3\}\},\; \{\backslash \; color\; \{blue\}\; d\_\; \{4\})\; \})\}$	Хэмминга (7,4)		Хэмминга (7,4) с дополнительным битом четности (Хэмминг (8,4))
	Передано. $(p\; 1,\; п\; 2,\; d\; 1,\; п\; 3,\; d\; 2,\; d\; 3,\; d\; 4)\; \{\backslash \; displaystyle\; (\{\backslash \; color\; \{red\}\; p\_\; \{1\}\},\; \{\backslash \; color\; \{red\}\; p\_\; \{2\}\},\; \{\backslash \; color\; \{\; синий\}\; d\_\; \{1\}\},\; \{\backslash \; color\; \{красный\}\; p\_\; \{3\}\},\; \{\backslash \; color\; \{синий\}\; d\_\; \{2\}\},\; \{\backslash \; color\; \{синий\}\; d\_\; \{3\}\},\; \{\backslash \; color\; \{синий\}\; d\_\; \{4\}\})\}$	Диаграмма	Передано. $(p\; 1,\; p\; 2,\; d\; 1,\; p\; 3,\; d\; 2,\; d\; 3,\; d\; 4,\; p\; 4)\; \{\; \backslash \; displaystyle\; (\{\backslash \; color\; \{красный\}\; p\_\; \{1\}\},\; \{\backslash \; color\; \{red\}\; p\_\; \{2\}\},\; \{\backslash \; color\; \{blue\}\; d\_\; \{1\}\},\; \{\backslash \; color\; \{red\}\; p\_\; \{3\}\}),\; \{\backslash \; color\; \{blue\}\; d\_\; \{2\}\},\; \{\backslash \; color\; \{blue\}\; d\_\; \{3\}\},\; \{\backslash \; color\; \{blue\}\; d\_\; \{4\}\},\; \{\backslash \; color\; \{green\}\; p\_\; \{4\}\})\}$	Диаграмма
0000	0000000		00000000
1000	1110000		11100001
0100	1001100		10011001
1100	0111100		01111000
0010	0101010		01010101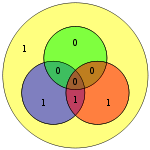
1010	1011010		10110100
0110	1100110		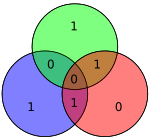11001100
1110	0010110		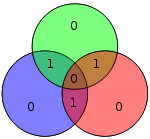00101101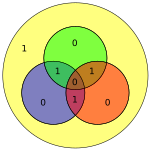
0001	1101001		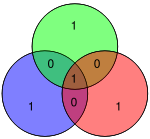11010010
1001	0011001		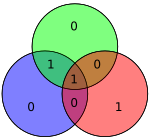00110011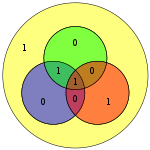
0101	0100101		01001011
1101	1010101		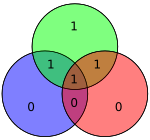10101010
0011	1000011		10000111
1011	0110011		01100110
0111	0001111		00011110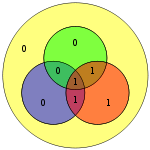
1111	1111111		11111111

Хэмминга ( 7,4) код тесно связан с E7решеткой и, фактически, может быть использован для ее построения, точнее, ее двойственной решетки E 7 (аналогичная конструкция для E 7 использует двойной код [7,3,4] 2). В частности, если взять набор всех векторов x в Z с x, конгруэнтным (по модулю 2) кодовому слову Хэмминга (7,4), и изменить масштаб на 1 / √2, получится решетка E 7

$E\; 7\; \ast \; =\; 1\; 2\; \{x\; \in \; Z\; 7:\; x\; mod\; 2\; \in \; [7,\; 4,\; 3]\; 2\}.\; \{\backslash \; displaystyle\; E\_\; \{7\}\; ^\; \{*\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{\backslash \; sqrt\; \{2\}\}\}\; \backslash \; left\; \backslash \; \{x\; \backslash \; in\; \backslash \; mathbb\; \{Z\}\; ^\; \{7\}:\; x\; \backslash ,\; \{\backslash \; bmod\; \{\; \backslash ,\}\}\; 2\; \backslash \; in\; [7,4,3]\; \_\; \{2\}\; \backslash \; right\; \backslash \}.\}$

Это частный пример более общего отношения между решетками и кодами. Например, расширенный (8,4) -код Хэмминга, который возникает в результате добавления бита четности, также связан с решеткой E8.

.

• Проблема программирования, связанная с Код Хэмминга (7,4)