Центрированное многоугольное число

Центрированные многоугольные числа представляют собой класс серии фигурных чисел, каждый образована центральной точкой, окруженной многоугольными слоями с постоянным числом сторон. Каждая сторона многоугольного слоя содержит на одну точку больше, чем сторона в предыдущем слое, поэтому, начиная со второго многоугольного слоя, каждый слой с центрированным k-угольным числом содержит на k точек больше, чем предыдущий слой.

• 1 Примеры
  • 1.1 Центрированные квадратные числа
  • 1.2 Центрированные шестиугольные числа
• 2 Формула
• 3 Сумма обратных чисел
• 4 Ссылки

Каждый элемент в последовательности кратен предыдущему треугольному числу плюс 1. Это можно формализовать уравнением $ax\; (x\; +\; 1)\; 2\; +\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{ax\; (x\; +\; 1)\}\; \{\; 2\}\}\; +\; 1\}$где a - количество сторон многоугольника, а x - порядковый номер, начиная с нуля для начального 1. Например, числа центрированного квадрата в четыре раза больше треугольника. числа плюс 1 или, что эквивалентно $4\; x\; (x\; +\; 1)\; 2\; +\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{4x\; (x\; +\; 1)\}\; \{2\}\}\; +\; 1\}$.

Эти серии состоят из

• центрированные треугольные числа 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199,... (OEIS : A005448 )
• квадратные числа с центрированием 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265,... (OEIS : A001844 )
• по центру пятиугольные числа 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331,... (OEIS : A005891 )
• шестигранные числа с центром 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397,... (OEIS : A003215 ), которые являются точной разницей последовательных кубов, то есть x - (x - 1)
• центрированные семиугольные числа 1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463,... (OEIS : A069099 )
• восьмиугольные числа с центрированием 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529,... (OEIS : A016754 ), которые в точности соответствуют нечетные квадраты
• неугольные числа с центром 1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595,... (OEIS : A060544 ), которые включают все четные совершенные числа, кроме 6
• центрированных десятиугольных чисел 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661,... (OEIS : A062786 )
• 1, 12, 34, 67, 111, 166, 232, 309, 397, 496, 606, 727,... (OEIS : A069125 )
• 1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793,... (O EIS : A003154 ), которые также являются звездочками

и так далее.

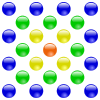
На следующих диаграммах показано несколько примеров центрированных многоугольных чисел и их геометрическое построение. Сравните эти диаграммы с диаграммами в Многоугольное число.

центрированное. треугольное. число	центрированное. квадрат. число	центрированное. пятиугольное. число	центрированное. шестиугольное. число

центрированное квадратное число

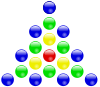1		5		13		25
		. .		. . . .		. . . . . .

центрированное шестиугольное число

1		7		19		37
		. .		. . . .		. . . . . .

Как видно на приведенных выше диаграммах, n-е центральное k-угольное число может быть получено путем размещения k копий (n-1) -го треугольного числа вокруг центральной точки; следовательно, n-е центрированное k-угольное число может быть математически представлено как

$C\; k,\; n\; =\; kn\; 2\; (n\; -\; 1)\; +\; 1.\; \{\backslash \; displaystyle\; C\_\; \{k,\; n\}\; =\; \{\backslash \; frac\; \{kn\}\; \{2\; \}\}\; (n-1)\; +1.\}$

Разность n-го и (n + 1) -го последовательных центрированных k-угольных чисел равна k (2n + 1).

n-е центральное k-угольное число равно n-му регулярному k-угольному числу плюс (n-1).

Как и в случае с правильными многоугольными числами, первое центрированное k-угольное число равно 1. Таким образом, для любого k, 1 одновременно является k-угольным и центрированным k-угольным числом. Следующее число, которое будет одновременно k-угольным и центрированным k-угольным, можно найти по формуле:

$k\; 2\; 2\; (k\; -\; 1)\; +\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{k\; ^\; \{2\}\}\; \{2\}\; \}\; (k-1)\; +1\}$

который говорит нам, что 10 одновременно является треугольным и центрированным треугольником, 25 является квадратным и центрированным квадратом и т. д.

Тогда как простое число p не может быть многоугольным числом (за исключением тривиального случая, т. е. каждый p является вторым p-угольным числом), многие центрированные многоугольные числа являются простыми числами. Фактически, если k ≥ 3, k ≠ 8, k ≠ 9, то существует бесконечно много центрированных k-угольных чисел, которые являются простыми числами (при условии гипотезы Буняковского ). (Поскольку все центрированные восьмиугольные числа также являются квадратными числами, и все центрированные неагональные числа также являются треугольными числами (и не равны 3), поэтому оба они не могут быть простыми числами)

сумма из обратных чисел для центрированных k-угольных чисел равна

$2\; \pi \; К\; 1–8\; К\; загар\; \; (\pi \; 2\; 1–8\; К)\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{2\; \backslash \; pi\}\; \{к\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{8\}\; \{k\}\}\}\; \}\}\}\; \backslash \; tan\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{8\}\; \{k\}\}\}\}\; \backslash \; right)\}$, если k ≠ 8

$\pi \; 2\; 8\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; pi\; ^\; \{2\}\}\; \{8\}\}\}$, если k = 8

• Neil Sloane Саймон Плафф (1995). Энциклопедия целочисленных последовательностей. Сан-Диего: Academic Press. : Fig. M3826
• Weisstein, Eric W. «Центрированное многоугольное число». MathWorld.
• F. Тэпсон (1999). Оксфордский словарь изучения математики (2-е изд.). Издательство Оксфордского университета. С. 88–89. ISBN 0-19-914-567-9.