В теории химических графов, индекс Винера (также число Винера ), введенный Гарри Винером, представляет собой топологический индекс молекулы , определяемый как сумма длин кратчайших путей между всеми парами вершин в химическом графе, представляющих не атомы водорода в молекуле.
Индекс Винера назван в честь Гарри Винера, который ввел его в 1947 году; в то время Винер называл это «числом пути». Это самый старый топологический индекс, связанный с ветвлением молекул. Основываясь на этом успехе, многие другие топологические индексы химических графов, основанные на информации в матрице расстояний графа, были разработаны после работы Винера.
Эта же величина также изучалась в чистой математике в рамках различные названия, включая общий статус, расстояние до графика и передачу. Индекс Винера также тесно связан с центральностью близости вершины в графе, величиной, обратно пропорциональной сумме всех расстояний между данной вершиной и всеми другими вершинами, которая часто используется в социометрия и теория социальных сетей.
бутан (C4H10) имеет два разных структурных изомера : н-бутан с линейной структурой из четырех атомов углерода. и изобутан с разветвленной структурой. Химический граф для н-бутана представляет собой четырехвершинный граф путей, а химический граф для изобутана - это дерево с одной центральной вершиной, соединенной с тремя листьями.
н-бутан
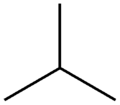
Изобутан
Молекула н-бутана имеет три пары вершин на расстоянии одна друг от друга, две пары на расстоянии два и одну пару на расстоянии трех, поэтому его индекс Винера равен

Молекула изобутана имеет три пары вершин на расстоянии друг от друга (три пары лист-центр) и три пары на расстоянии два (пары лист-лист). Следовательно, его индекс Винера равен

Эти числа являются экземплярами формул для особых случаев Винера индекс: это 



Таким образом, даже если эти две молекулы имеют одинаковую химическую формулу и одинаковые числа углерод-углеродных и углерод-водородных связей, их разная структура дает разные индексы Винера.
Винер показал, что индекс Винера тесно коррелирует с точками кипения молекул алкана. Более поздняя работа над количественными соотношениями структура – активность показала, что они также коррелируют с другими величинами, включая параметры его критической точки, плотности, поверхности натяжение и вязкость его жидкой фазы, а также площадь ван-дер-ваальсова поверхности молекулы.
Индекс Винера может быть вычислен непосредственно с использованием алгоритма для вычисления всех попарных расстояний на графике. Когда граф не взвешен (так, что длина пути - это просто количество его ребер), эти расстояния могут быть вычислены путем повторения алгоритма поиска в ширину один раз для каждой начальной вершины. Общее время для этого подхода составляет O (nm), где n - количество вершин в графе, а m - количество его ребер.
Для взвешенных графиков вместо этого можно использовать алгоритм Флойда – Уоршалла или алгоритм Джонсона с временем работы O (n) или O (nm + n log n) соответственно. Альтернативные, но менее эффективные алгоритмы, основанные на многократном умножении матриц, также были разработаны в литературе по химической информатике.
Когда нижележащий граф является дерево (как, например, для алканов, первоначально изученных Винером), индекс Винера может быть рассчитан более эффективно. Если граф разделен на два поддерева путем удаления единственного ребра e, то его индекс Винера представляет собой сумму индексов Винера двух поддеревьев вместе с третьим членом, представляющим пути, проходящие через e. Этот третий член может быть вычислен за линейное время путем вычисления суммы расстояний между всеми вершинами от e в каждом поддереве и умножения двух сумм. Этот алгоритм разделяй и властвуй может быть обобщен с деревьев на графы с ограниченной шириной дерева и приводит к алгоритмам, близким к линейному времени для таких графов.
Альтернативный метод для вычисления индекса Винера дерева, авторы Боян Мохар и Томаж Писански, обобщают задачу на графы со взвешенными вершинами, где вес пути является произведением его length с весами двух его конечных точек. Если v является листовой вершиной дерева, то индекс Винера дерева может быть вычислен путем слияния v с его родителем (сложения их весов вместе), вычисления индекса результирующего меньшего дерева и добавления простого поправочного члена для путей которые проходят через ребро от v до его родителя. Повторно удаляя листья таким образом, индекс Винера может быть вычислен за линейное время.
Для графов, построенных как произведения более простых графов, индекс Винера графа произведения часто может может быть вычислен по простой формуле, которая объединяет индексы его факторов. Бензеноиды (графы, образованные путем склеивания правильных шестиугольников ребром к ребру) могут быть вложены изометрически в декартово произведение трех деревьев, что позволяет вычислить их винеровские индексы за линейное время с использованием формулы произведения вместе с алгоритмом линейного временного дерева.
Gutman Yeh (1995) рассмотрел проблему определения того, какие числа могут быть представлены как индекс Винера графа. Они показали, что все положительные целые числа, кроме двух, имеют такое представление; два исключения - числа 2 и 5, которые не являются индексом Винера любого графа. Для графов, которые должны быть двудольными, они обнаружили, что снова могут быть представлены почти все целые числа с большим набором исключений: ни одно из чисел в наборе
можно представить как индекс Винера двудольного графа.
Гутман и Йе предположили, но не смогли доказать, аналогичное описание чисел, которые могут быть представлены как индексы Винера деревьев, с набором из 49 исключительных значений:
Гипотеза была позже доказана Вагнером, Вангом и Ю.